基于Fuzzy-AHP的河岸边坡稳定性综合评判

雷金兴，王瑞，赵坤

（中国建筑第六工程局有限公司，天津300451）

1 引言

河岸边坡稳定性评判是一项比较复杂的系统工程。自然岩土体由于其自身的复杂性与场地的多样性，使得河岸边坡的稳定性受到多种因素的制约与影响。这些因素之间的关系错综复杂，它们会以不同的组合模式对河岸边坡的稳定性产生完全不同的影响效力[1]。因此，河岸边坡的稳定性评判是一种基于多指标多层级的系统性综合评判问题。

近年来，国内外研究人员针对边坡系统的特点，将神经网络、灰色聚类、模糊综合评判等多种学科、多种理论引入边坡稳定性评判，取得丰硕的成果。20世纪70年代，层次分析法首次被应用于解决复杂的、难以定量研究的问题。黄建文等[2]将层次分析法融入模糊数学理论，并应用在高边坡稳定性评价方面，说明该方法在简化计算等方面存在的优势。曾胜等[3]将Fuzzy-AHP评判应用在堆积体边坡稳定性评价中。彭东黎等[4]针对公路膨胀土边坡特点，建立评价指标体系来对模糊综合评判进行应用。王佳信等[5]讨论了一种因子分析-概率神经网络方法来对典型边坡进行稳定性评判。这些研究大多针对岩质边坡或特殊工程性质的边坡，而将模糊综合评价应用在河岸边坡稳定性分析的研究较少。为此，本文中，基于广泛调查研究河岸边坡稳定性影响因素的条件下，构建稳定性评价指标体系，对河岸边坡稳定性进行快速有效的科学评判。

2 Fuzzy-AHP评判方法

2.1 方法及步骤

Fuzzy-AHP评判方法，是将模糊数学理论(Fuzzy)与层次分析法(AHP)结合起来的一种综合评价方法。其中，模糊综合评判是基于模糊数学理论，面向多种模糊因素影响的对象的总体综合评判；层次分析法是基于网络系统理论与多目标综合评价方法，而建立的层次权重决策方法。本文中，将Fuzzy-AHP评判方法应用到河岸边坡稳定性评价，构建出基于层次分析法的边坡稳定性Fuzzy-AHP评判模型。具体思路为：首先建立河岸边坡的稳定性评价指标体系，利用层次分析法计算各稳定性评价因子的权重，最后根据模糊评判矩阵对河岸边坡的稳定性进行评判，计算出稳定性评判结果。

2.2 河岸边坡评价指标体系

综合考虑国内外学者对河岸边坡稳定性影响因素的研究结果，并在大量调查长江流域多处河岸边坡的基础上[6]，选取与稳定性评判现场应用有指导意义的4类16项指标进行分析，构建可以良好反映河岸边坡特征的模糊层次分析体系，如图1所示。并且，参照河岸边坡的稳定性程度，将其稳定性划分为4个等级区间：一级（稳定）、二级（较稳定）、三级（较不稳定）、四级（不稳定或破坏），如表1所示。

图1 河岸边坡稳定性评价指标体系

表1 河岸边坡稳定性评价分级标准

2.3 模糊综合评判

2.3.1 指标权重的确定

采用AHP方法来确定各评价指标的权重。根据文中构建的指标评价体系，通过各个指标间相互重要性对比构建判断矩阵来确定权重向量。该方法首先对同层次指标按照1～9标度法来构建重要性判断矩阵F，即：

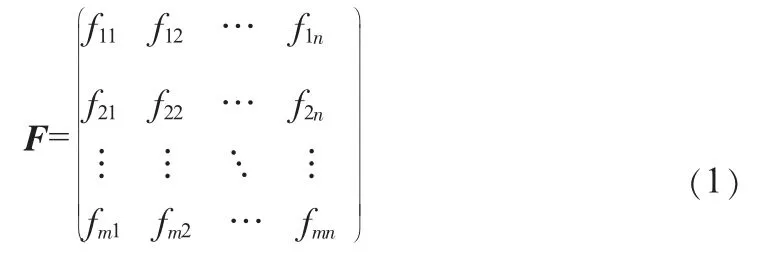
式中，fij为指标i与指标j根据1～9标度表比较得到的重要性定量标度；fij=1/fij。

计算其最大特征向量λmax及相应的归一化特征向量W，即为模型各指标的权重向量，最后，参照一致性检验规则，验证权重分配是否合理。

以河岸地质状况为例：

1）构建判断矩阵F1为：

2）计算得到最大特征值（即权重）为λmax=5.02，对应的归一化特征向量（即权向量）为：

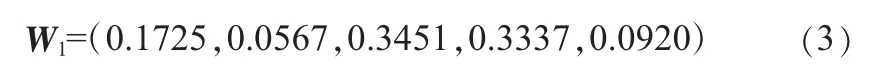
3）一致性检验。判断矩阵阶数m=5，查一致性检验表后计算得到一致性指标CR=0.036＜0.1。所以，矩阵达到一致性要求，权重设置合理。

经过两两指标层次分析，计算得到河岸边坡其他评价指标的权重。结果如表2所示。

表2 各评价指标权重

2.3.2 隶属度的确定

进行模糊评判的关键是计算各级评价指标uij对各级分级标准νi的隶属度，即建立隶属函数μi(x)。参考文献[4]在膨胀土边坡稳定性多级评判中将风险等级通过分值区间进行量化的方式，对于4个分级标准进行等效量化，如表3所示。同时，据此对各评价指标也进行量化处理，由此建立每个指标的评判标准，结果如表4所示。

表3 河岸边坡稳定性分级量化标准

表4 各评价指标分级量化标准

在得到各评价指标的评价等级评分值Q之后，再通过隶属度函数确定其对每个稳定性等级的隶属度。本文中，隶属度函数采取三角形分布函数形式，各评价等级隶属度计算式为：

求得各指标对等级隶属度为：

等级隶属度矩阵为：

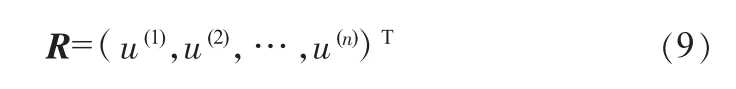
式中，n为评价体系中评价指标数量；q为评分值；u(n)为第n个评价指标的等级隶属度。

2.3.3 多级模糊综合评判模型

河岸边坡稳定性评判指标系统具有多层次结构，需要通过多级综合评判判定。计算时，二级综合评判的结果向量所构成的矩阵设为一级评判的判断矩阵，求得最终的评价结论B。

本文采用最大隶属度原则，B中最大隶属度相应的稳定性分级就是多级模糊综合评判的最终结果。

3 工程应用

为验证本文提出的河岸边坡稳定性多级综合评判方法的适用性，利用本方法对重庆江津白沙长江大桥P2主塔一侧岸坡进行稳定性评价。白沙长江大桥工程区属构造剥蚀浅丘地貌，河谷横断面呈U形分布。P2主塔一侧岸坡整体高差约70 m，总体呈折线形，平均坡度34°，植被覆盖率57%。岸坡形态为凸岸，上覆层为较薄的冲击层粉土～砂土，下伏基岩为砂质泥岩夹砂岩，无滑坡历史。施工过程中，对部分坡体进行了平场爆破开挖，并在岸坡下部12 m范围内进行了混凝土挂网喷护。

在评判过程中，选择正常工况与洪水工况2种情况进行对比。正常工况下近岸侧水深15 m，江水流速1.5 m/s，风浪作用较弱，无降雨。洪水工况参考2020年长江第五号洪峰过境白沙时的工况，近岸侧水深26.5 m，江水流速4.2 m/s，风浪作用较强，日降雨量28 mm。

3.1 正常工况

根据该边坡宏观参数和现场状况，对照河岸边坡稳定性分级标准，对正常工况下各二级指标进行评分量化，进行模糊评判，结果如表5所示。

表5 各评价指标的隶属度向量

由此计算最终的结论向量：

参照最大隶属度原则，本河岸边坡在正常工况下稳定性评价结果为二级，处在较稳定状态。该评价结果与现场勘查报告描述基本相同。

3.2 洪水工况

洪水工况下仅有水文气象等各项评价指标发生变化。计算得到水文气象的评价结果向量为

最终的结论向量：

参照最大隶属度原则，本河岸边坡在正常工况下稳定性评价为三级，处在较不稳定状态，必须进行一定的加固防护。这与洪水过后，该河岸边坡下部发生部分垮塌，坡面防护结构发生大面积损毁现象一致。

4 结论

1）建立了考虑河岸边坡工程实际的二级Fuzzy-AHP分析模型，对较多且复杂的河岸边坡稳定性影响因素进行了评判，有效解决了由于影响因素过多而难以量化各指标权重及影响程度的问题。

2）通过工程实例验证了该模型的正确性与合理性，结论可靠，具有一定的优越性。可以为白沙长江大桥后期的运营维护提供一定的参考。

3）本文利用Fuzzy-AHP理论客观有效地评价了河岸边坡的稳定性。但是，由于河岸边坡本身的复杂性，其边坡稳定性评价指标体系还需在实际应用中逐步完善。