弹性支承上简支约束长矩形薄板面内剪切作用下屈曲行为分析
李君谊,莫时旭,郑艳
(1.桂林理工大学土木与建筑工程学院,广西 桂林541004;2.广西建筑新能源与节能重点实验室,广西 桂林541004)
1 引言
在国家大力推行下,钢-混组合结构在工程中得到广泛应用。矩形钢管混凝土在工程应用中,薄壁钢板受弯矩和剪力同时作用,易发生局部屈曲;薄壁钢-混凝土组合墙在抵抗水平作用时,钢板受剪切作用,也会发生屈曲。弹性支承上矩形板面内受压作用下的屈曲问题已有相关文献,而弹性支承上矩形板面内剪切受力条件下的屈曲问题国内相关研究较少。实际工程中已知薄板剪切屈曲的临界强度,可以避免其发生剪切屈曲,具有工程应用意义。
近年来,国内外学者对矩形薄板的屈曲问题进行了大量分析研究。国外学者Timshenko等[1]在能量法的基础上提出了不同情况下矩形薄板的弹性屈曲理论计算模型;国内学者边宇虹[2]用变分法对四边简支的矩形板的稳定问题进行了研究;莫时旭等[3]用Ritz能量变分法对方形钢管混凝土局部屈曲问题进行了试验研究;毛佳等[4]采用Ritz能量变分法对弹性支承上薄板屈曲进行了研究;童根树等[5]采用有限元法对四边简支矩形板在各联合作用下的弹性屈曲问题进行了研究分析;本文采用Rayleigh-Ritz法(瑞利-里兹法)推导了基于弹性基底的周边简支约束矩形板面内剪切受力条件下的屈曲理论计算公式,具有理论指导意义。
2 理论计算
Rayleigh-Ritz法,是应用势能驻值原理求解稳定问题的一种很重要的近似方法,此法采用具有几个广义坐标的位移函数近似地代替真实的位移曲线,将原来为无限个变量的泛函变分问题变为有限个变量的函数极值问题来处理。根据势能驻值原理的极值条件,用导数求极值问题的方法,可以将求解微分方程的问题变为求解代数方程的问题。
假设屈曲薄板的挠度曲面为下列级数形式:

式中,ai为待定参变数,称为广义坐标,i=1,2,3,…,n;φi(z)为满足几何边界条件的已知函数,z为自变量,φi为对应函数,这些函数任意选择且线性无关。
将公式(1)代入总势能∏=U+V的表达式,从而使总势能变为具有n个参变数ai的函数。这样,总势能的∏变分δ∏,δ∏=δ(U+V)就可以用与各参变数变分ai相对应的增量之和来表达:

式中,∏为总势能;U为弹性体应变能;V为外力势能。
若弹性体系的变形处于平衡状态,则应满足势能驻值条件,将公式(2)带入δ∏=0,得:

因为参变数ai变分是微小的任意数值,欲满足式(3),只有:

从而得到下列方程组:

此方程组有非零解的条件为系数行列式等于零,从而得到稳定方程式。解此稳定方程,即可求得平衡状态的荷载。
本文简支边界计算模型见图1,矩形薄板受剪屈曲后纵向为连续n个半波,即为n阶屈曲模态。

图1 简支边界计算简图
取一阶屈曲模态及二阶屈曲模态研究具有代表性,因此取位移函数为:

式中,A为位移函数中波长的振幅;a为矩形薄板长度;b为矩形薄板宽度;α为节线斜率;x、y分别为X方向和Y方向的分位移。
位移函数满足上下边界:

位移函数满足节线边界上:

式中,位移函数上下边界满足y=0,y=b时,位移函数ω(x,y)=0;节线边界满足ω对x求偏导数为0。
板弯曲应变能U、弹性支承势能Uk和轴向载荷Nxy及轴向荷载做功V分别为:
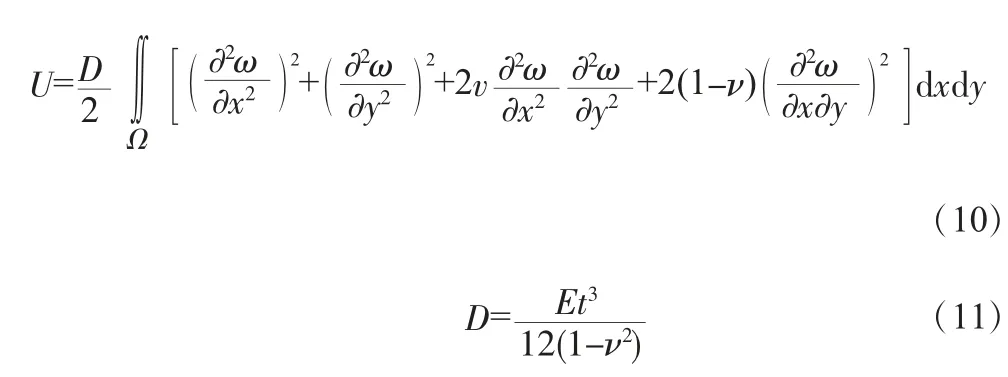
式中,U为板弯曲应变能;D为矩形薄板单宽抗弯刚度;E为钢材弹性模量;t为薄板厚度;ν为钢材泊松比。
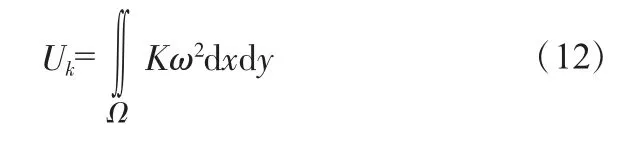
式中,Uk为弹性支承势能;K为弹性支承刚度;ω为矩形薄板受剪屈曲后的位移函数ω(x,y)。
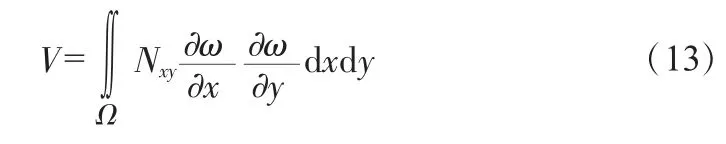
式中,V为轴向荷载做功;Nxy为轴向荷载。
根据最小势能原理,可求得临界状态的轴向荷载:

式中,κ为屈曲系数;b为矩形薄板宽度。
3 参数影响分析
3.1 长宽比影响分析
假设弹性支承刚度K=0,取不同的长宽比γ(γ≥1.5),然后对节线斜率α求导,求出使屈曲系数κ取最小值的节线斜率α,最后带入α得出临界屈曲系数(见表1),临界屈曲系数与不同长宽比的关系,如图2所示。

图2 本文与文献[1]简支边界κ-γ曲线
由表1可以得出:对于长矩形薄板(γ≥1.5),本文理论计算值与文献[1]的计算值平均偏差为9.16%;对于长矩形薄板(γ≥2),偏差小于1.67%。在工程实际应用中长矩形薄板(γ≥2)的情况更多。

表1 简支边界下不同长宽比的临界屈曲系数
3.2 支承刚度影响分析
假设矩形薄板长为2 m,宽为1 m(γ=2),即方形薄板;板厚为0.03 m;钢材弹性模量为2.1×1011Pa;取不同的K,得出相应的临界屈曲系数(见表2),临界屈曲系数与支承刚度的关系如图3所示。

图3 本文简支边界κ-K曲线

表2 简支边界下不同支承刚度的临界屈曲系数
由图3可以得出:临界屈曲系数随着支承刚度的单调递增,即支承刚度越大,对长矩形薄板的侧向约束越强,临界屈曲系数越大。
4 结论
1)本文采用Rayleigh-Rite法计算弹性支承上简支约束长矩形薄板面内剪切作用下临界屈曲系数,计算所得的临界屈曲系数与文献[1]计算所得数据略有偏差,证明此理论方法可行。
2)弹性支承的刚度越大,对长矩形薄板的侧向边界约束越强,长矩形薄板屈曲越困难。
3)对于高阶屈曲形态的长矩形薄板,如纵向屈曲为n个斜向半波,可假设函数为来求解,从而得出在不同长宽比下完整的临界屈曲系数曲线。
——《势能》

