Outage Performance and Optimal Design of MIMO-NOMA Enhanced Small Cell Networks with Imperfect Channel-State Information

Zheng Shi,Hong Wang,Yaru Fu,Guanghua Yang,Shaodan Ma,Xinrong Ye

1 School of Intelligent Systems Science and Engineering,Jinan University,Zhuhai 519070,China

2 State Key Laboratory of Internet of Things for Smart City and the Department of Electrical and Computer Engineering,University of Macau,Macao 999078,China

3 School of Communication and Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

4 School of Science and Technology,Hong Kong Metropolitan University,Hong Kong SAR,China

5 School of Physics and Electronic Information,Anhui Normal University,Wuhu 241002,China

Abstract:This paper focuses on boosting the performance of small cell networks(SCNs)by integrating multiple-input multiple-output(MIMO)and nonorthogonal multiple access(NOMA)in consideration of imperfect channel-state information(CSI).The estimation error and the spatial randomness of base stations(BSs)are characterized by using Kronecker model and Poisson point process(PPP),respectively.The outage probabilities of MIMO-NOMA enhanced SCNs are first derived in closed-form by taking into account two grouping policies,including random grouping and distance-based grouping.It is revealed that the average outage probabilities are irrelevant to the intensity of BSs in the interference-limited regime,while the outage performance deteriorates if the intensity is sufficiently low.Besides,as the channel uncertainty lessens,the asymptotic analyses manifest that the target rates must be restricted up to a bound to achieve an arbitrarily low outage probability in the absence of the inter-cell interference.Moreover,highly correlated estimation error ameliorates the outage performance under a low quality of CSI,otherwise it behaves oppositely.Afterwards,the goodput is maximized by choosing appropriate precoding matrix,receiver filters and transmission rates.In the end,the numerical results verify our analysis and corroborate the superiority of our proposed algorithm.

Keywords:imperfect channel-state information(CSI);multiple-input multiple-output(MIMO);non-orthogonal multiple access(NOMA);small cell networks(SCNs)

I.INTRODUCTION

With the surge of wireless data traffic and number of mobile devices,it has become increasingly imperative for 5G cellular networks to offer an improved spectrum efficiency as well as massive connectivity[1,2].As per Cisco visual networking index(VNI)[3],5G speeds are estimated to be 13 times higher than the average mobile connection by 2023,and the number of mobile devices is forecasted to grow from 8.8 billion in 2018 to 13.1 billion by 2023.To confront these unprecedented challenges,small cell has been recognized as one of the promising solutions for 5G to deliver ever-increasing network capacity and fulfill the accommodation of a large number of users[4].However,aggressive frequency reuse will incur severe interference for ultra-dense small cell deployment[5].To remedy this issue,the fusion of small cell networks(SCNs)and other key enabling 5G technologies has received enormous interest[5—7].Specifically,the combination of multiple-input multiple-output(MIMO)and non-orthogonal multiple access(NOMA)is anticipated to considerably improve spectral efficiency and support more concurrent connections for interference-infested SCNs[8—12].

1.1 Related Works and Motivations

Since MIMO attains additional spatial diversity gain by deploying multiple antennas and NOMA exploits extra multi-user diversity gain by taking advantage of the channel discrepancy,it has been vastly reported that MIMO-NOMA achieves superior performance over its orthogonal counterpart,i.e.,MIMOorthogonal multiple access(OMA),in terms of both the reliability and the spectral efficiency[13—16].Nevertheless,the application of MIMO-NOMA to SCNs still remains in its infancy.Notwithstanding,a wide range of investigations on single-input single-out(SISO)-NOMA enhanced SCNs have been conducted in the literature[5,17,18].To mention only a few,by assuming single antenna at both small cell base stations(BSs)and users,the coverage probability and achievable rate of non-uniform SCNs were examined in[5].By considering large-scale networks,it was studied in[17]that the coverage probability of small cells depends heavily on the prescribed transmit rates and power sharing coefficients.In addition,a novel energy-efficient algorithm was proposed for NOMA aided heterogeneous SCNs with energy harvesting by assuming perfect channel-state information(CSI)in[18].Unfortunately,prior works seldom touched MIMO-NOMA enhanced SCNs except for[8,9].In particular,the authors in[8]substantiated the superior performance of MIMO-NOMA over MIMO-OMA in multi-cell systems in terms of the ergodic sum-rate.Besides,a new interference mitigation and power allocation scheme was invented for downlink MIMONOMA assisted heterogeneous SCNs[9].However,the existing literature commonly assume perfect CSI at the receivers without the practical consideration of imperfect CSI in MIMO-NOMA enhanced SCNs.

Unfortunately,there are only few available methodologies that can be leveraged to undertake the performance investigations into MIMO-NOMA enhanced SCNs with imperfect CSI.To be specific,K.Heet al.developed a novel compressed sensing-aided MIMONOMA scheme by allowing for imperfect CSI in[19],where an upper bound for the performance of the proposed scheme was presented by using restricted isometry property.In[20],the worst-case Gaussian approximation was employed to derive the total sum rate,with which the significant spectral and energy efficiency gains over the existing multi-way relay network were demonstrated.A semi-closed expression was provided for the outage performance evaluation of multiple-input single-output(MISO)-NOMA in view of imperfect CSI in[21],in which the assumption of correlated CSI was made.In[22],Gaussian approximation was used to derive the outage probability of MIMO-NOMA systems under imperfect CSI.For the sake of analytical tractability,the uncorrelated estimation errors were assumed and only power allocation was involved into precoding without accounting for beamforming design in[22].However,the developed methodologies in[19—22]are based on either approximations or simulations,and they cannot be directly applied into the scenario of large-scale SCNs as well.Moreover,although a large-scale dense network was considered in[23],the proposed analytical approach is specific to the multiple-input single-output(MISO)-NOMA system.In contrast,the performance analysis of the MIMO-NOMA system will introduce the difficulty of handling random matrix variate.

This motivates us to trigger the performance investigations of MIMO-NOMA enhanced large-scale SCNs with imperfect CSI at both the transmit and receive sides.More specifically,Poisson point process(PPP)and Kronecker model are utilized to capture the randomness of small cell BSs’positions and the impact of estimation error correlation,respectively.By employing stochastic geometry and integral transform,the exact outage probabilities are derived in closed-form and insightful results are extracted by conducting asymptotic outage analyses.With the analytical results,the optimal design of MIMO-NOMA enhanced SCNs is empowered.To the best of our knowledge,this is the first work that copes with MIMO-NOMA enhanced SCNs under imperfect CSI.Additionally,in contrast to[13,14,22],a more flexible MIMO-NOMA transmission framework with variable number of clusters/groups is established in this paper.Furthermore,it is worth noting that the Gaussian approximation used in[22]cannot be applied in this paper because of the nonexistence of mean and variance of the aggregated inter-cell interference.

1.2 Contributions

To recapitulate,five main contributions of this paper are enumerated below.

1.Exact compact expressions are derived for the outage probabilities of MIMO-NOMA enhanced SCNs,where two NOMA grouping policies are considered,namely random NOMA grouping and distanced-based NOMA grouping.

2.The exact outage analyses show that the average outage probability is irrespective of the intensity of BSs in the interference-limited regime.Whereas,a counterintuitive behavior that the intensity of BSs below a threshold is harmful to the average outage performance is observed.

3.As the channel uncertainty vanishes,the target transmission rates should be upper bounded to guarantee an arbitrarily low outage probability in the absence of the inter-cell interference.

4.The correlation coefficient has a positive effect on the outage probability under the high quality of CSI.Conversely,the correlation coefficient impairs the outage performance if the quality of CSI is low.

5.The goodput maximization of the MIMO-NOMA system is considered by jointly devising the precoding matrix,receiver filters and transmission rates.Numerical results exhibit that the proposed scheme outperforms other benchmarking schemes especially under significant difference between channel gains,including MIMO-OMA with precoding,MIMO-OMA without precoding and MIMO-NOMA without precoding.

1.3 Paper Organization and Notation

The remaining of the paper is organized as follows.Section II delineates the model of MIMO-NOMA enhanced SCNs.The exact and asymptotic outage analyses are carried out in Sections III and IV,respectively.Section V devotes itself to the optimal system design.Numerical results are then presented for validations in Section VI.Section VII finally concludes this paper.

II.SYSTEM MODEL

This paper considers a MIMO-NOMA enhanced SCNs with imperfect CSI.We assume that the positions of the small cell BSs obey a homogeneous PPP Φbof intensityλband the users are also distributed according to a homogenous PPP Φuof intensityλu.Each user is associated with its closest BS[24,25].The BSs and the users are equipped withMandNantennas,respectively.By considering heavily loaded networks,i.e.,λu ≫λb,it is reasonable to assume that there are at least 2Kusers in a typical Voronoi cell andK ≤min{M,N}[26,27].To accommodateKpairs of NOMA users over MIMO channels within the coverage of each cell,2Kusers can be randomly chosen in the Voronoi cell.Accordingly,the NOMA users are uniformly distributed within the Voronoi cell[24].In[26,28,29],the distance between a user and its serving BS approximately follows a Rayleigh distribution with probability density function(PDF)

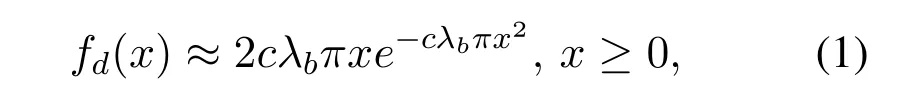
wherec= 5/4.Hereinafter,the system model is introduced by splitting into three subsections,including transmission model,imperfect CSI and received SINR.

2.1 Transmission Model

In this paper,the NOMA scheme is implemented in the power-domain.By following the similar MIMONOMA framework to[14],theK ×1 informationbearing vector s sent by a typical BSzis expressed as

2.2 Imperfect CSI

2.3 Received SINR

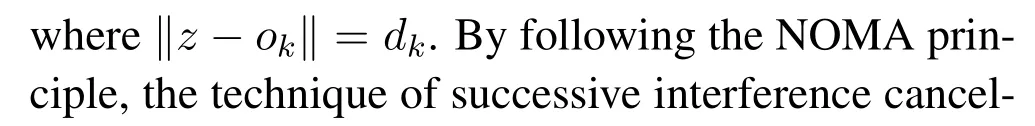
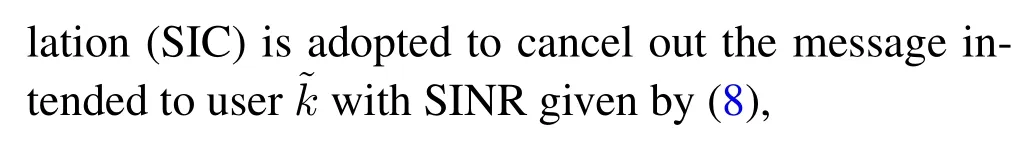
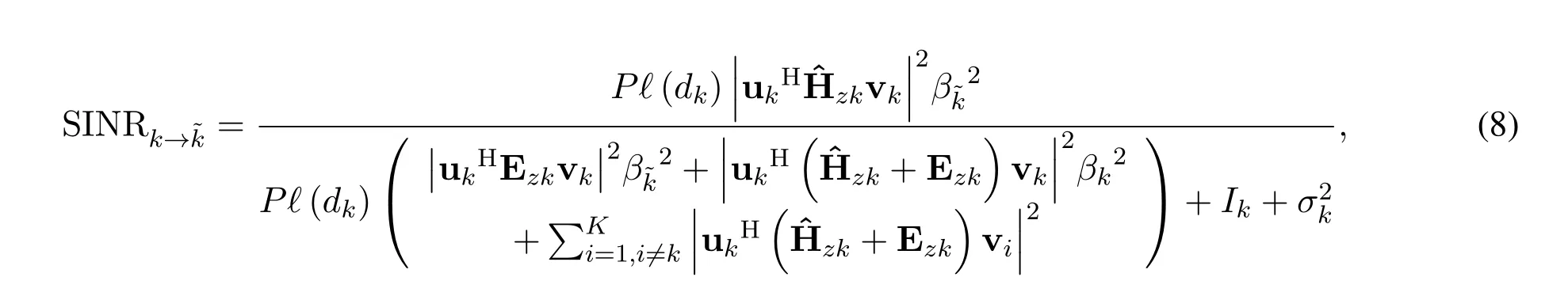
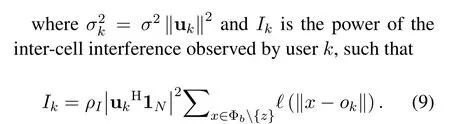
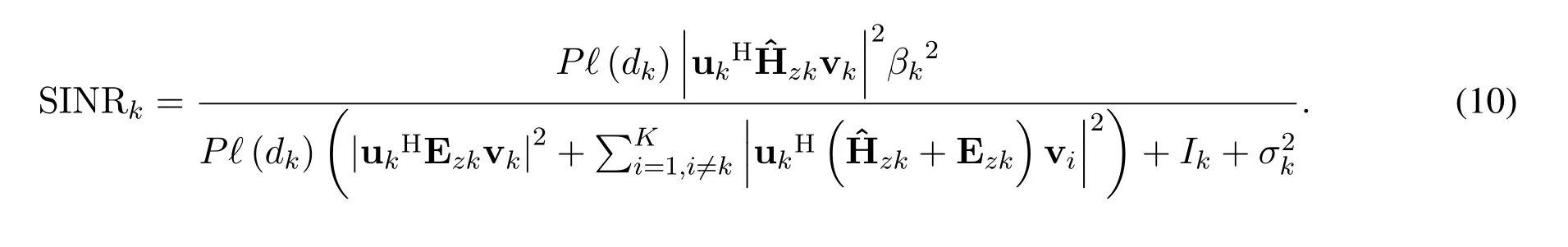
In an analogous way,the far userdecodes its ownmessage with SINR given by(11),

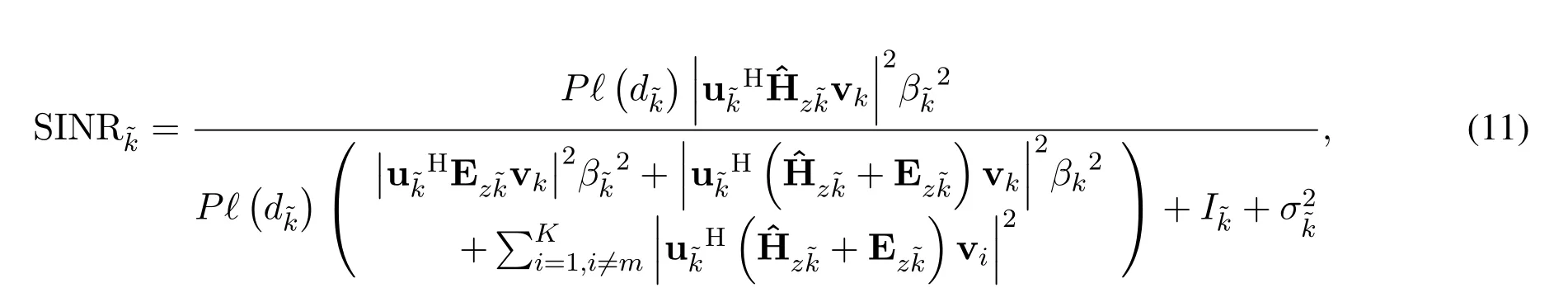
III.OUTAGE PROBABILITY

Since the outage probability is the key performance metric,this section is dedicated to conducting the outage analysis for MIMO-NOMA enhanced SCNs with imperfect CSI.The outage probabilities of users~kandkare separately derived as follows.

3.1 Outage Probability of the Far User ~k

3.1.1 Conditional Outage Probability

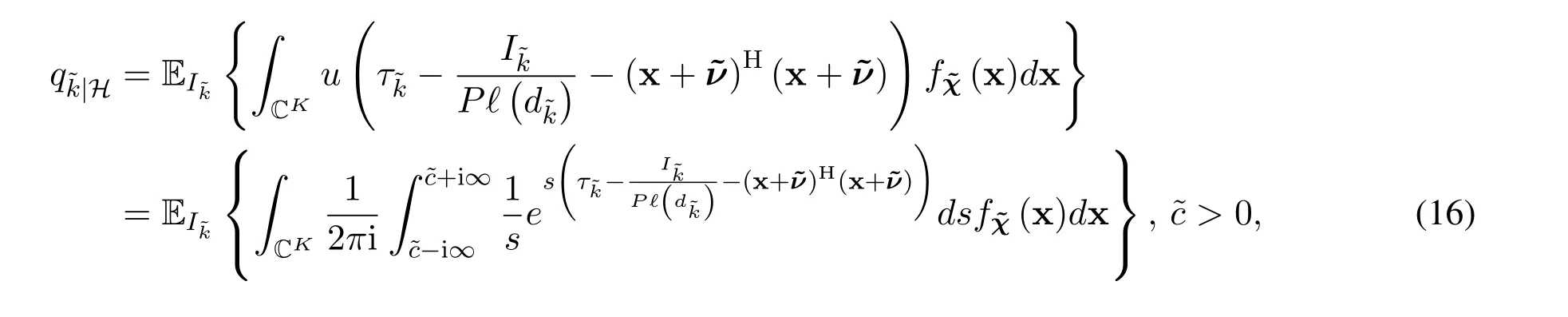
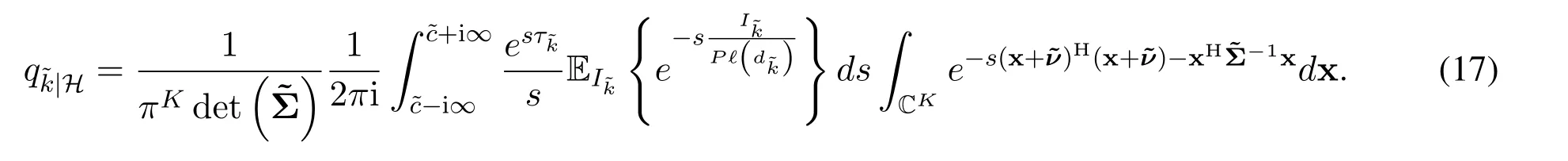
By using the sum of two quadratic forms[31,eq.8.1.7]and the important integration[30,eq.22],the inner integral in(17)can be computed as

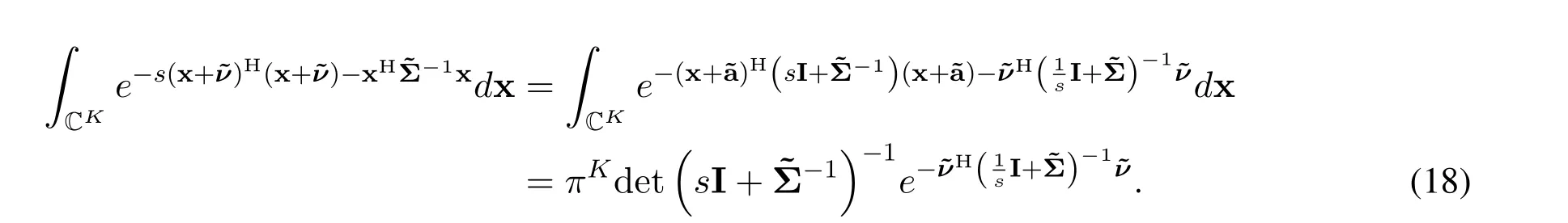
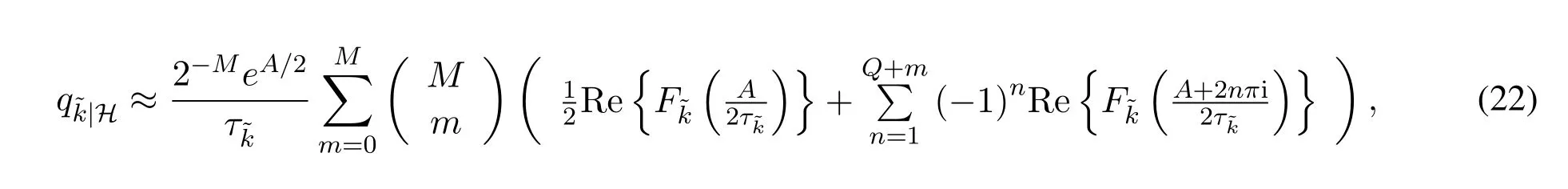
whereMrefers to the number of Euler summation terms,Qrefers to the truncation order,the discretization error is bounded by|ϵ|≤e－A/(1-e－A)and the truncation error is manageable by properly choosingMandQ.To have a discretization error up to 10－10,Ais set toA ≈23.As suggested by[33],M= 11 andQ=15 are typically chosen.

By putting(22)into(13),we can get the final expression of the conditional outage probabilitypk|H.

3.1.2 Average Outage Probability

Furthermore,the average outage probability by taking the expectation over the distancecan be expressed as

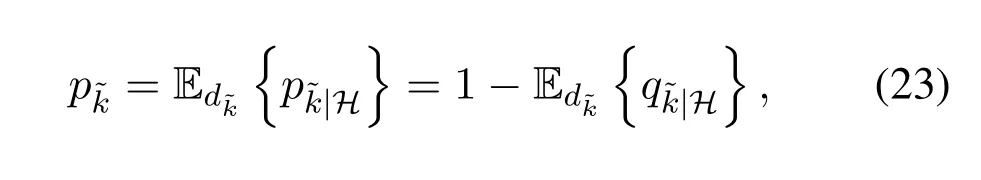
where

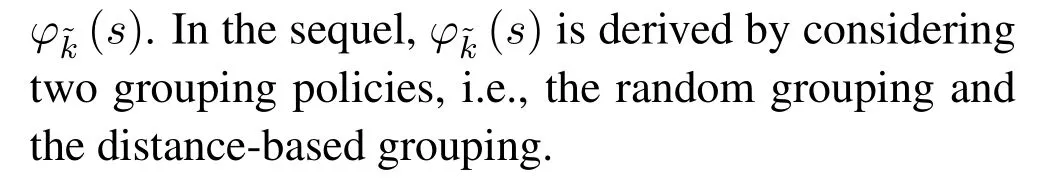
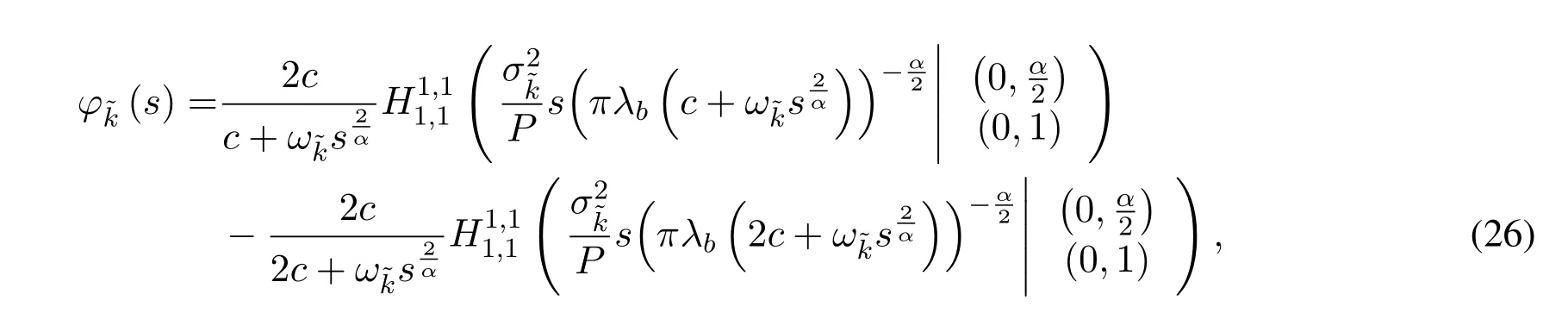
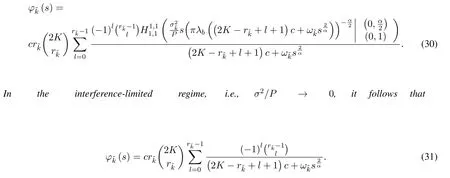
3.2 Outage Probability of the Near User k

3.2.1 Conditional Outage Probability

By conducting the SIC at the near user,the near user has to subtract the far user’s signal prior to decoding its own signal.Hence,the conditional outage probability of userkgivenHis given by(33).

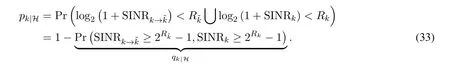
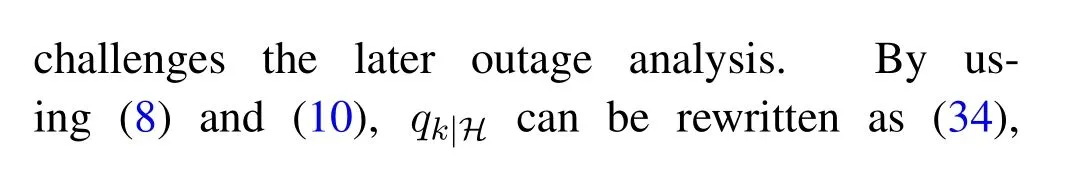
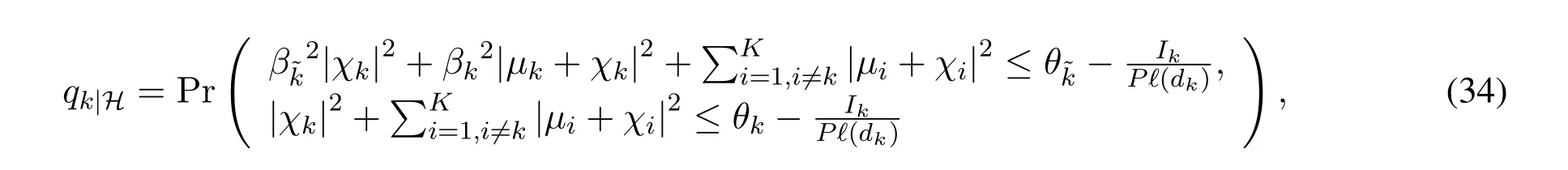
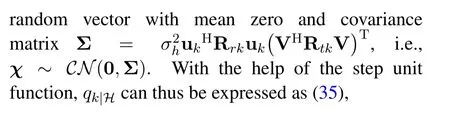
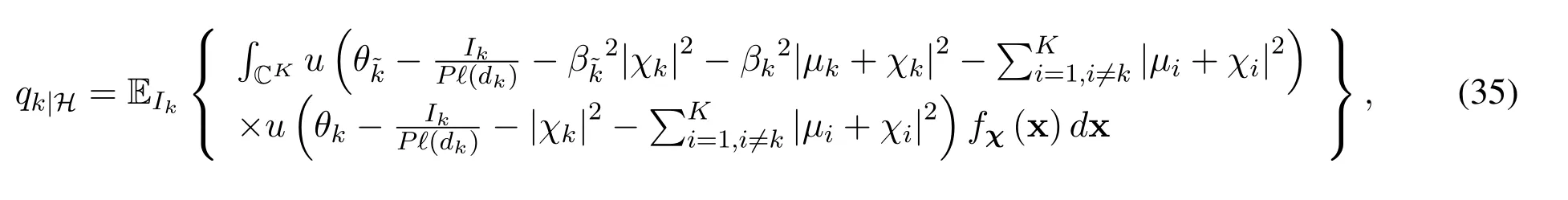
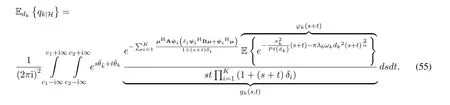
wherefχ(x)stands for the joint PDF ofχandfχ(x)= exp(-xHΣ－1x)/(πKdet(Σ)).In analogous to(16),by using the inverse Laplace transform of the step unit function along with some rearrangements,qk|Hcan be obtained as(36),

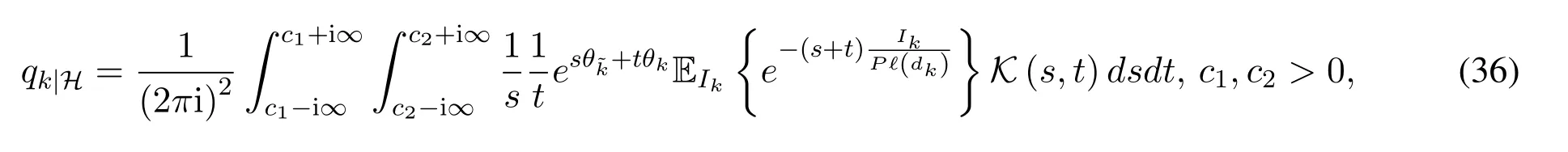
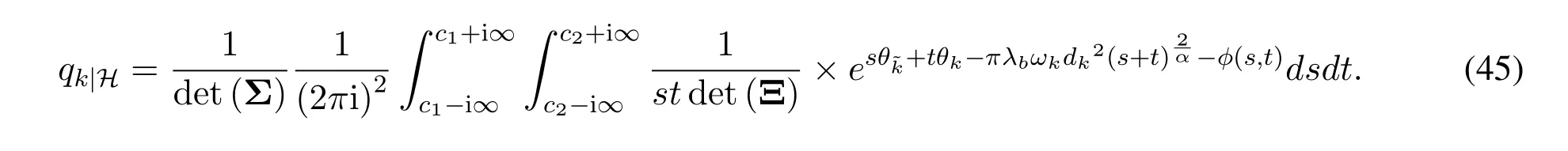
Moreover,by capitalizing on eigenvalue decomposition Σ=ΨΔΨH,defining Ψ=(ψ1,···,ψK)and Δ = diag(δ1,···,δK),φ(s,t)in(45)can be simplified as

As a consequence,qk|His derived as(47).

The above two-dimensional inverse Laplace transform can be obtained by means of the Moorthy algorithm[36].More specifically,is approximated by adopting a trapezoidal rule of integration as(48),

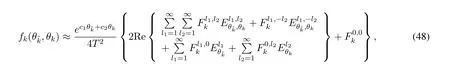
where the parameterTdetermines the sampling period,Lis the truncation order,

3.2.2 Approximate Expression ofpk|H

Unfortunately,the two-dimensional numerical inversion of Laplace transform entails considerable computation burden,which precludes to the real-time optimal system design.In what follows,an approximate expression ofpk|His derived to combat this dilemma.By overlooking the dependence between SINRk→~kand SINRk,pk|His approximated by using(33)as

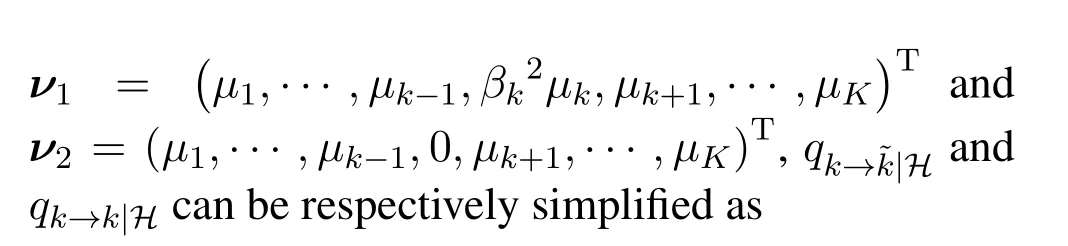
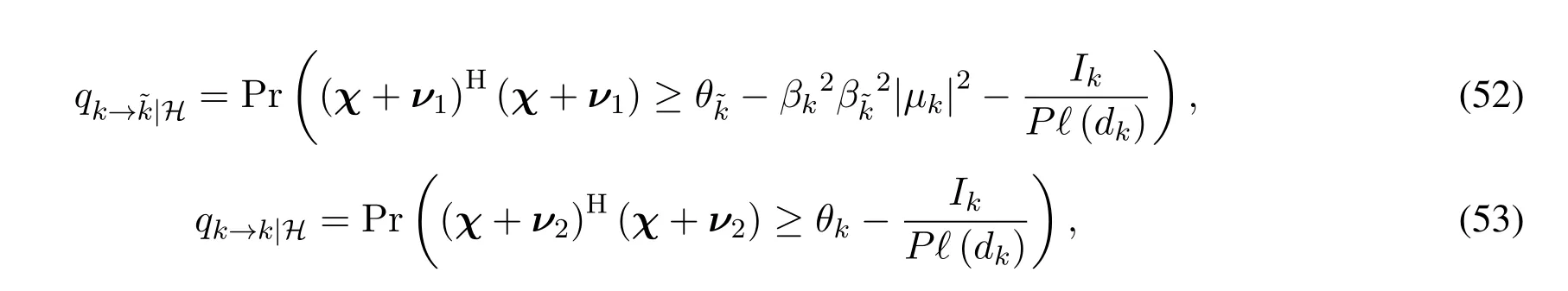
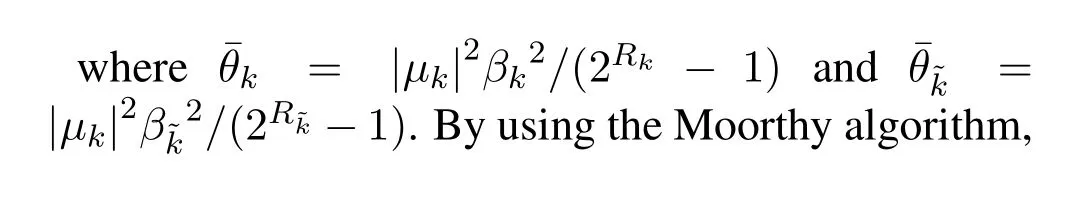
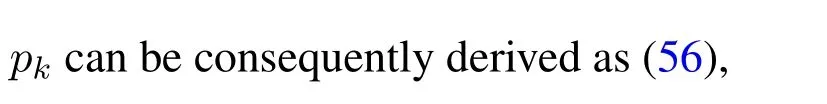
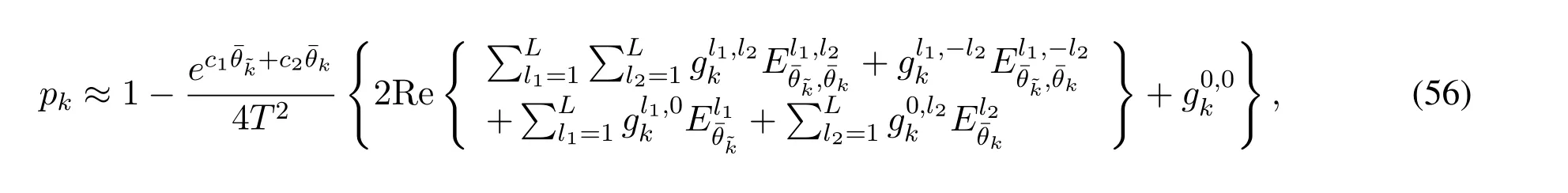
IV.ASYMPTOTIC OUTAGE ANALYSI S

Unfortunately,the exact outage expressions are too cumbersome to gain extra helpful insights.To address this issue,this section seeks to investigate the asymptotic behavior of the outage probability as the quality of CSI improves,i.e.,Kzk →∞or.For simplicity and tractability,we specialize our analysis to the case of no inter-cell interference,i.e.,λb= 0.Similarly to[25],the tool of Chernoff bound is resorted to offer upper bounds for the outage probabilities.The asymptotic outage probabilities of the far and near users are individually discussed by splitting into two subsections.

4.1 Asymptotic Outage Probability of the Far User ~k

It should be highlighted that Theorem 5 differs from the results in[25],where only a single data stream is considered.Besides,a loose upper bound ofis provided in[25].Particularly,the simulation results in Section VI justify the correctness of Theorem 5.However,it is worth mentioning that the same property does not carry over to the case ofλb /= 0,that is,an arbitrary low outage target cannot be warranted for any nonzero target rates.

4.2 Asymptotic Outage Probability of the Near User k

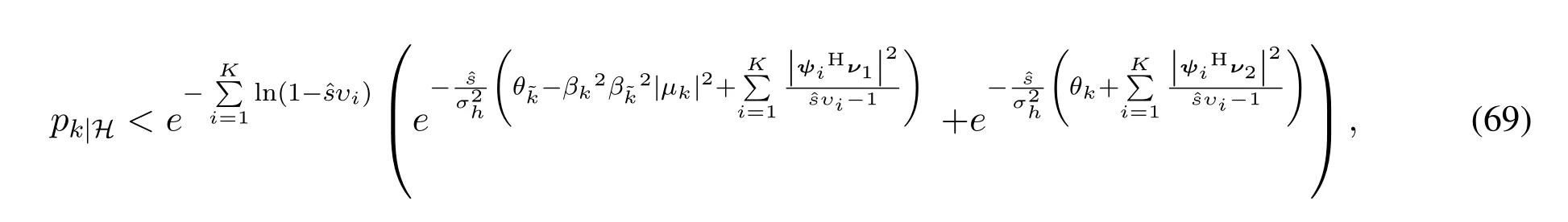
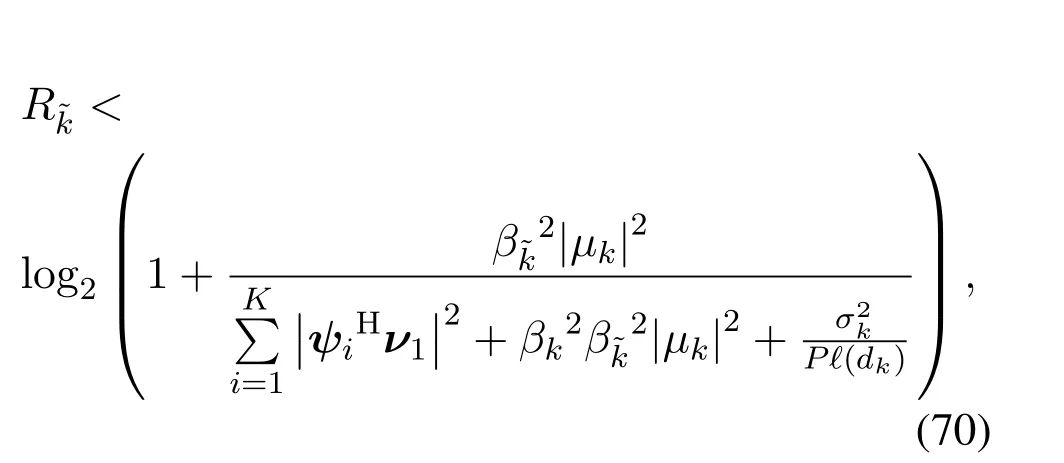
V.OPTIMAL SYSTEM DESIGN

By making use of the foregoing analytical results,the parameters of MIMO-NOMA enhanced SCNs can be properly configured to adapt to the imperfect fading channels while ensuring the quality of service,including the precoding matrix(i.e.,V),receiver filters(i.e.,power allocation coefficients(i.e.,and the transmission rates(i.e.,To exemplify this,we confine our attention to maximize the long-term goodput that measures the number of successfully conveyed information bits per transmission[39—41].Given the known channel informationH,the conditional goodput of the MIMO-NOMA system is expressed as

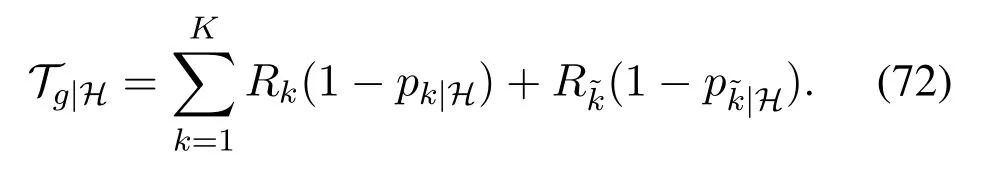
Thereon,the maximization of goodput while guaranteeing low outage constraints is posed by(73),

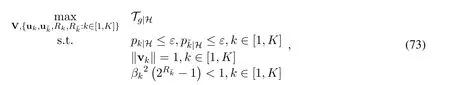
whereεdenotes the maximum endurable outage probability.In general,the power allocation coefficientsβkand transmission ratescannot be jointly optimized in(73)in order to not violate the intention of NOMA principle.This is because as disclosed by[42],the joint optimization ofβkandwould behave like waterfilling algorithm if the user fairness is disregarded,that is,all the power would be allocated to the users under benign channel conditions and no information bits would be delivered to the users experienced bad channel conditions.In light of this observation,we fix the power allocation coefficient to maintain the user fairness in the sequel.

Unfortunately,due to the complex outage expressions,it is virtually impossible to get the globally optimal solution to(73).To tackle this difficulty,the concept of the signal/interference alignment proposed by[14]is applied to choose an appropriate V,ukandwith low implementation overhead1.In particular,in order to substantially suppress the inter-pair interference,it is necessary to impose the constraints onThis leads to

Algorithm 1.The selection of the precoding matrix V.1:for i=1 to M!/(M -K)!do 2:L ←Yi,Yi is a matrix of size M ×K that contains exactly one entry of 1 in each column,at most one entry of 1 in each row and 0s elsewhere;3:Find uk,u~k by using[14,Algorithm 1];4:Construct G =(g1,···,gK)H,where gkH =ukH ˆHzkL and k ∈[1,K];5:Get the effective channel gain for each user pair,γk =1/(G－1G－H)k,k;6:Find the smallest effective channel gain,i.e.,γmin,i =min{γ1,···,γK};7:end for 8:Find the index i that maximizes the smallest effective channel gain,i.e.,i* =arg max γmin,i;9:V ←LG－HD,where L=Yi*.i∈[1,M!/(M－K)!]

VI.NUMERICAL ANALYSIS

6.1 Verifications

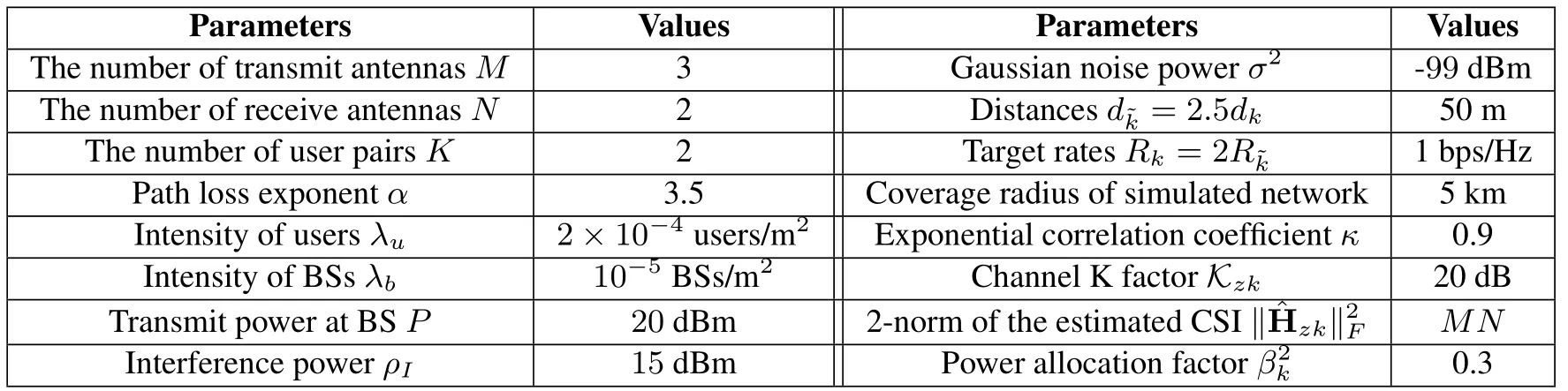
Table 1.Simulation parameters.

Figure 2 plots the conditional outage probabilitypk|Hagainst the channel K factorKzk.As expected,the analytical results coincide with the simulation ones.Moreover,asKzkincreases,the outage probability decays to an outage floor.It is no doubt that the outage floor is determined by the co-channel interference from surrounding BSs.

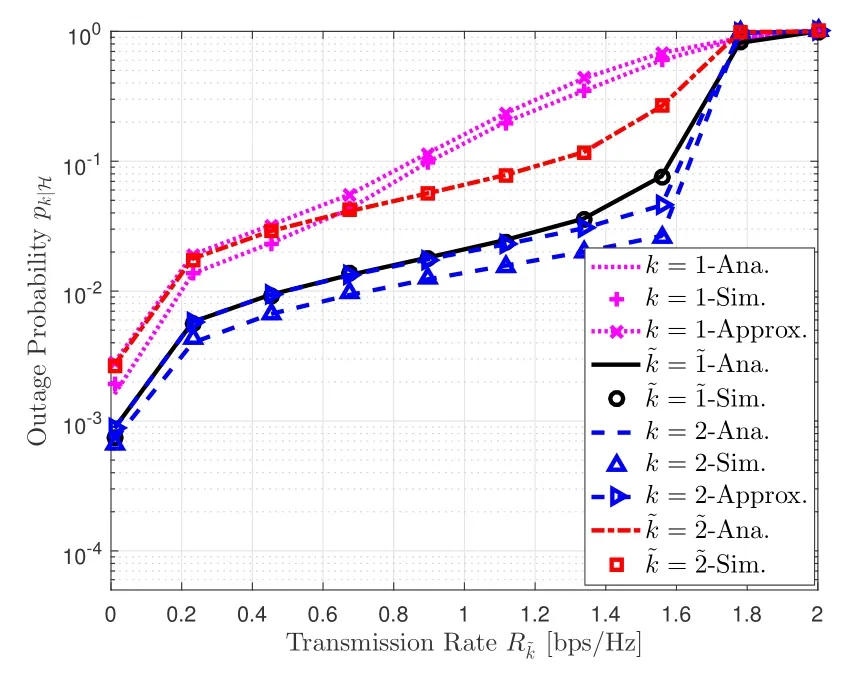
Figure 1.The conditional outage probability pk|H versus the transmission rate by setting parameters as.

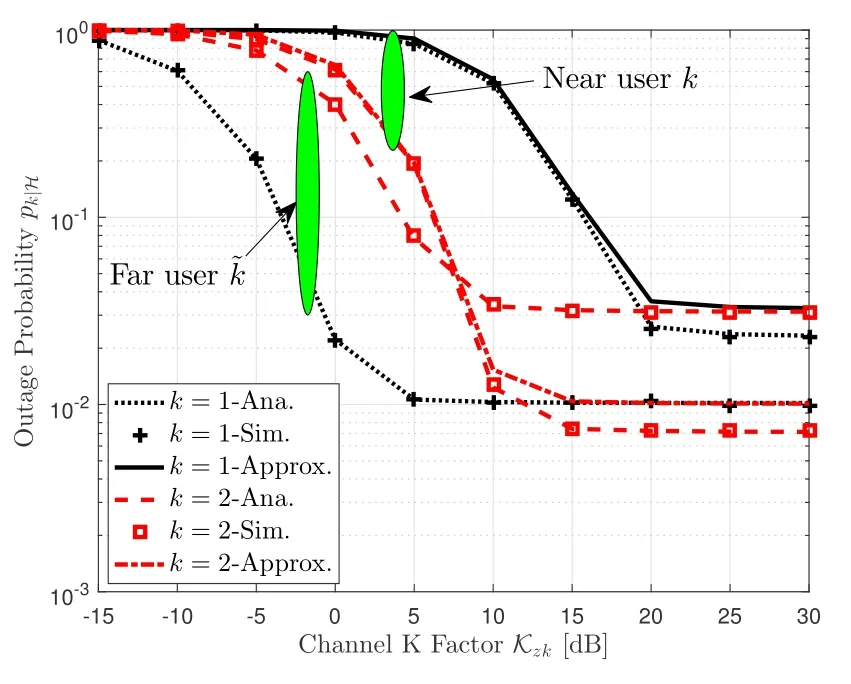
Figure 2.The conditional outage probability pk|H versus the channel K factor Kzk by setting bps/Hz.

Figure 3 investigates the average outage probabilitypkagainst the transmission rate.In both Figs.3 and 4,the exact and approximate outage probabilities of the random grouping policy(labeled as“Random-Exact”and“Random-Approx.”)for far(or near)NOMA user are calculated by using(26)(or(57))and(27)(or(58)),respectively.Moreover,the simulated outage probability(labeled as“Random-Sim.”)is plotted for verification.Similarly,the numerical results for the distance-based grouping policy can be obtained according to Theorems 2 and 4,and the corresponding exact,approximate and simulated outage probabilities are labeled as“Distance-Exact”,“Distance-Approx.”and“Distance-Sim.”,respectively.From Figure 3,we observe a perfect match between the analytical and simulation results,which corroborates the validity of our analysis.It can also be seen that the distance-based grouping policy performs better than the random grouping policy in terms of the outage probability of the near user,while the impact on the outage probability of the far user behaves differently.This is due to the fact that the near/far user under the distance-based grouping policy is closer to/-farther away from its associated BS than that under random grouping policy.Nevertheless,it is noteworthy that the random grouping policy is frequently used for benchmarking purpose,because it has been intensively investigated in[44]and[45]that the random grouping policy provides the lowest sum rate gain.

Figure 4 depicts the average outage probabilitypkagainst the intensity of BSsλb.Aside from the similar findings as Figure 3,it is evident that the average outage probability is irrelevant to the intensity of BSs under highλb,i.e.,interference-limited regime.This is consistent with our analytical results.Nonetheless,the average outage performance declines ifλbfalls below a threshold(e.g.,10－6BSs/m2).Indeed,such observations seem to be counterintuitive since the inter-cell interference is alleviated asλbdecreases.However,the decrease ofλbalso signifies the expansion of the size of Voronoi cell,on average,this dominant effect engenders severe path loss.

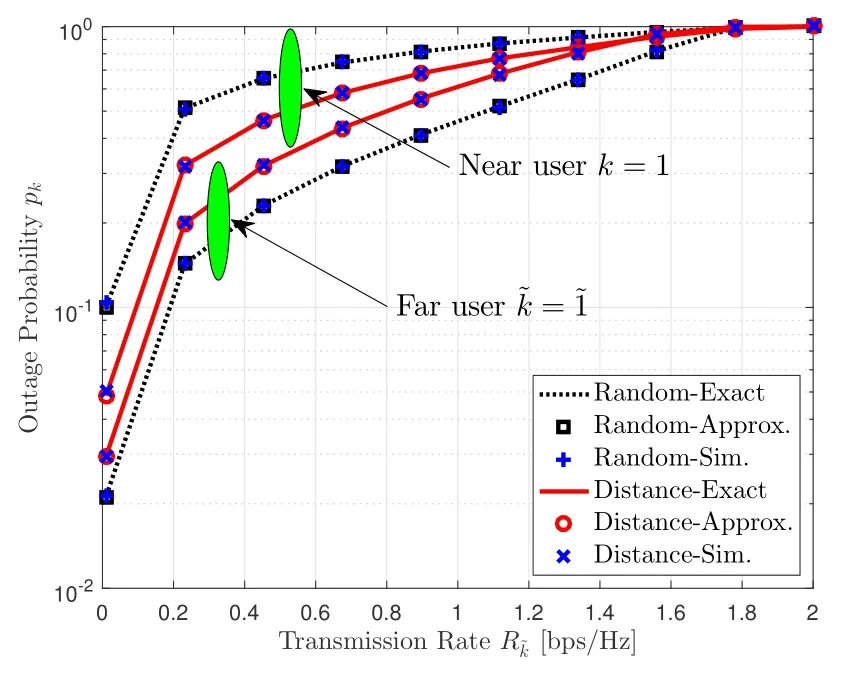
Figure 3.The average outage probability pk versus the transmission rate by setting.

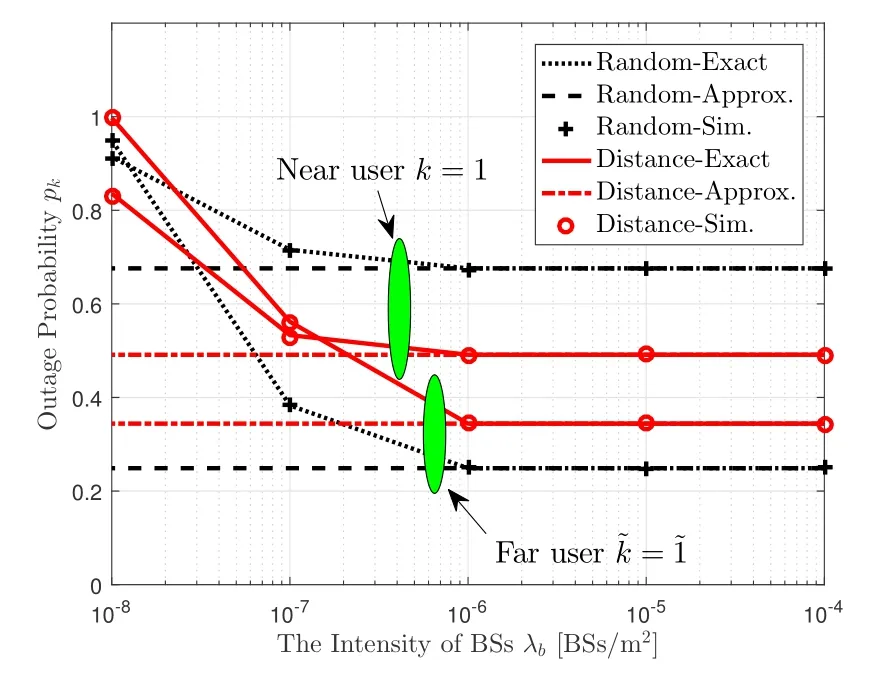
Figure 4.The average outage probability pk versus the transmission rate by settingbps/Hz.

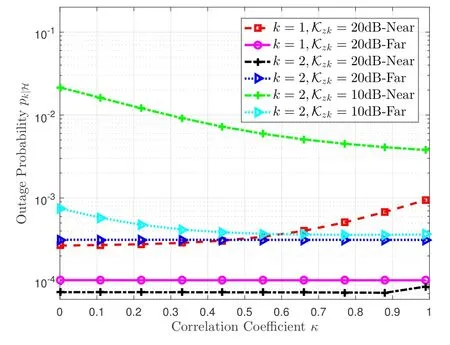
Figure 5.The conditional outage probability pk|H versus the exponential correlation coefficient κ with parameters and λb =10-7BSs/m2.

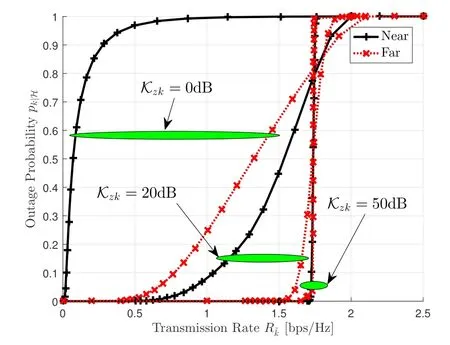
Figure 6.The conditional outage probability pk|H versus the transmission rate by settingand λb =0 BSs/m2.

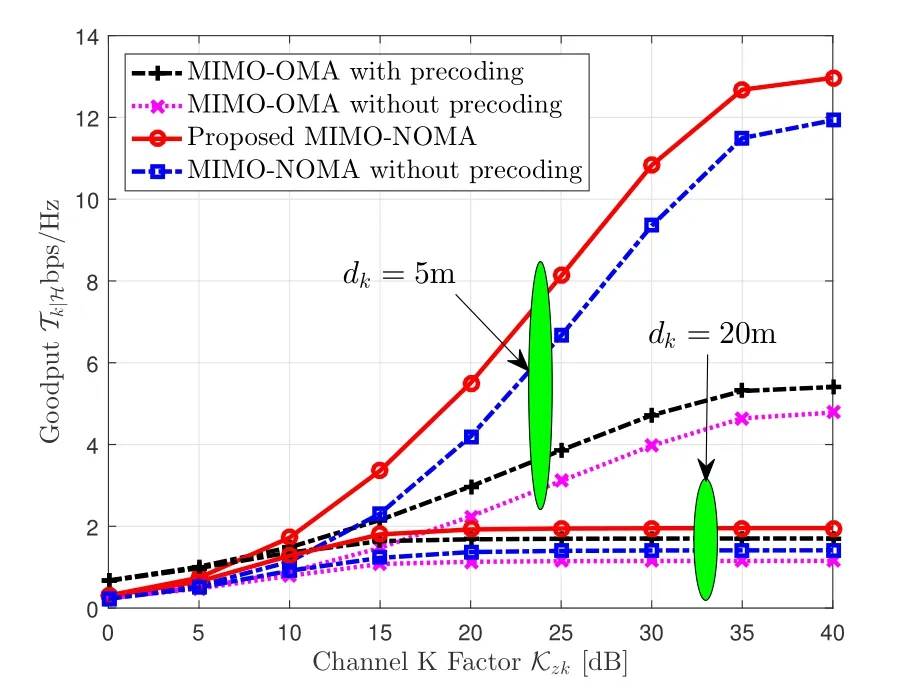
Figure 7.Performance comparison with the three baseline schemes in terms of the goodput Tk|H versus the channel K factor Kzk with ε=10-2.

6.2 Impacts of System Parameters

6.3 Optimal System Design

VII.CONCLUSION

The performance of MIMO-NOMA enhanced SCNs has been thoroughly investigated by taking into account the assumption of imperfect CSI.The channel estimation error and the spatial randomness of BSs have been characterized by capitalizing on Kronecker correlation model and homogeneous PPP,respectively.The outage probabilities of MIMO-NOMA systems have been derived in compact form by considering two distinct NOMA grouping policies,including the random grouping and the distance-based grouping.It has been proved that the average outage probabilities are independent of the intensity of BSs in the interferencelimited regime.Interestingly,it has been found that the outage performance is degraded under a sufficiently low intensity of BSs.Besides,the asymptotic analyses have been carried out to gain more insights into the outage behavior under high quality of CSI.Specifically,it has been shown that the target rates must be limited up to a bound to achieve an arbitrarily low outage probability in the absence of inter-cell interference.The outage expressions have empowered the maximization of the goodput by properly designing the precoding matrix,receiver filters and transmission rates.At last,the numerical results have also revealed that the estimation error correlation contributes to improve the outage performance under low quality of CSI.Whereas,opposite observations have been made under high quality of CSI.Furthermore,for intelligent resource allocation of NOMA enhanced SCNs,we plan to extend the machine-learning based approaches as in[46]and[47]to our future work.

ACKNOWLEDGEMENT

This work was supported in part by the National Key Research and Development Program of China under Grant 2017YFE0120600,in part by National Natural Science Foundation of China under Grants 61801192,62171200,and 61801246,in part by Guangdong Basic and Applied Basic Research Foundation under Grant 2019A1515012136,in part by Natural Science Foundation of Anhui Province under Grant 1808085MF164,in part by the Science and Technology Planning Project of Guangdong Province under Grants 2018B010114002 and 2019B010137006,in part by the Science and Technology Development Fund,Macau SAR(File no.0036/2019/A1 and File no.SKL-IOTSC2021-2023),in part by the Hong Kong Presidents Advisory Committee on Research and Development(PACRD)under Project No.2020/1.6,in part by Qinglan Project of University of Jiangsu Province,and in part by the Research Committee of University of Macau under Grant MYRG2018-00156-FST,in part by 2018 Guangzhou Leading Innovation Team Program(China)under Grant 201909010006.

NOTES