Multi-Task Deep Learning Based Hybrid Precoding for mmWave Massive MIMO System

Zhongjie Li,Wei Gao,Min Zhang,Jiyuan Xiong

School of Electronics and Information Engineering,South Central University for Nationalities,Wuhan 430074,China

Abstract:Due to the different signal-to-noise ratio(SNR)of each subchannel,the bit error rate(BER)of hybrid precoding based on singular value decomposition(SVD)decreases.In this paper,we propose a multi-task learning based precoding network(PN)model to solve the BER loss problem caused by SVD based hybrid precoding under imperfect channel state information(CSI).Specifically,we firstly generate a dataset including imcomplete CSI input channel matrix and corresponding output labels to train the PN model.The output labels are designed based on uniform channel decomposition(UCD)which decomposes the channel into multiple subchannels with same gain,while the vertical-bell layered space-time structure(V-BLAST)signal processing technology is combined to eliminate the inner interference of the subchannels.Then,the PN model is trained to design the analog and digital precoding/combining matrix simultaneous.Simulation results show that the proposed scheme has only negligible gap in spectrum efficiency compared with the fully digital precoding,while achieves better BER performance than SVD based hybrid precoding.

Keywords:millimeter wave;massive MIMO;hybrid precoding;uniform channel decomposition;multitask learning

I.INTRODUCTION

Millimeter wave massive multi-input multi-output(MIMO)systems have become a promising technology for 5G communication thanks to their high data rate,low latency and high bandwidth at high frequencies.In massive MIMO communication systems,each antenna equipped with a radio-frequency(RF)chain to realize fully digital signal processing results in significant energy consumption and hardware complexity.Hybrid precoding structure decomposes the design of precoding into baseband precoding and analog precoding,which not only effectively reduce the number of RF chains but also provide sufficient performance.

In recent years,several hybrid precoding algorithms have been proposed.The author in[1]proposes spatial sparse hybrid precoding algorithm,which transforms the hybrid precoding design problem into sparse signal reconstruction.In[2],an alternate hybrid beamforming method is presented to optimize the achievable rate of the system.An iterative algorithm is proposed in[3]to optimize the system’s energy consumption.Existing research aims to design analog and digital precoder to minimize the approximation error between fully digital and hybrid solutions.In MIMO systems,the optimal capacity can be achieved by combining the water filling algorithm with SVD-based hybrid precoding.However,the singular value of the channel matrix will be significantly different due to the limited scattering properties of mmWave,resulting in a large gap between the signal-to-noise ratio(SNR)of each subchannel.

To address the aforementioned issues,an geometric mean decomposition(GMD)based hybrid precoding scheme is proposed in[4]to improve the BER performance by decomposing the MIMO channel into parallel subchannels with the same gain after eliminating the inner interference.Furthermore,a GMD based uniform channel decomposition(UCD)algorithm is proposed to solve the capacity loss problem and exploit diversity gain[5,6].More specifically,it has been show that the UCD algorithm can achieve high data rate transmission by decomposing MIMO channel into an arbitrary number of independent subchannels.

Deep learning(DL)emerged as a novel technology with the ability to effectively capture target features while reducing computational complexity has been successfully implemented in MIMO systems[7—11].Therefore,it is of great significance to apply deep learning to design the mmWave massive MIMO hybrid precoding.

Several deep learning based method bave been proposed for hybrid precoding design in the literature[12,13].The author in[12]proposed a Deep Neural Network(DNN)based hybrid precoding scheme for mmWave massive MIMO systems,where the activation functions create mapping relations and use gradient descend method to optimize the network.In[13],a Deep learning based hybrid precoding model is proposed for single user massive MIMO systems.But the model only considers the transmitter.In addition,most of the existing work has developed a two-step hybrid precoding scheme based on deep learning[14—16].The author in[14]proposed a hybrid precoding algorithm to jointly sense the channel and design the hybrid precoding.More specifically,the analog precoder design is transformed into selecting the best candidates in the array responses vector codebook,which is generated from the feasible set of array responses vectors.To generated the training labels,the author in[15]use the exhaustive search algorithm to calculate the hybrid precoding matrix which is used to training the deep learning model.Thus,the above work needs to obtain the hybrid precoding matrix through an existing algorithm for model training.In this setting,the performance of the two-step deep learning scheme is limited by the algorithms used to make corresponding label.

In this paper,we aim to reduce the performance constraints caused by labels making algorithms and minimize the approximation error between fully digital and hybrid solutions by simultaneously designing the analog and baseband precoding/combining matrix.To this end,a popular DL based multi-task learning(MTL)framework[17]is used,which leverages common information between related tasks to effectively improve the generalization performance.The main contributions of this paper are as follow:

1.A multi-task learning based scheme is proposed for hybrid precoding/combining design.In the scheme,we use the fully digital precoding matrix as corresponding label,and train the model by designing the analog and baseband precoder/combiner simultaneously,so as to reduce the performance limitation.Furthermore,the complex convolution neural network[18]is used for the reason that the transmitting signal and channel matrix belongs to the complex domain.

2.A very large training dataset is generated to train the PN model.More specifically,we use the UCD algorithm to calculate the full digital precoding/-combining matrix used as the corresponding labels in order to minimize the approximation error between fully digital and hybrid solution.Since the channel matrix of perfect CSI is difficult to obtain in reality,we use the channel matrix with noise as the input of the model and training the model to designs the hybrid precoding and combining matrix in the case of imperfect CSI.

3.In order to prevent the generation of the zero gradient in uniform quantization,each element in the RF matrix is quantized with an approximation quantization layer in the model.We also adopt a normalization layer to satisfy the power constraint and customize loss function to minimize the Frobenius distance between the label and the estimation matrix,while forcing the orthogonality of the estimation matrix.

4.We provide the computational complexity analysis for the proposed algorithm and compare their computational complexity with the conventional SVD and UCD algorithm.The simulation results show that the proposed method achieved better performance in terms of bit error rate and spectral efficiency in the case of imperfect CSI.

II.SYSTEMS MODEL

III.DATA GENERATION PROCESS

In order to train the model,the channel matrices and corresponding labels are needed to construct the training dataset.To complete the precoding and combining matrices design and eliminate interference,we combine the UCD algorithm with the ZF-VLAST scheme and use it as labels.In this section,we first review the ZF-VBLAST scheme and UCD algorithm.Then,introduce the dataset generation process.

3.1 ZF-VBLAST

3.2 UCD-VBLAST

3.3 TRAINING DATASET GENERATION

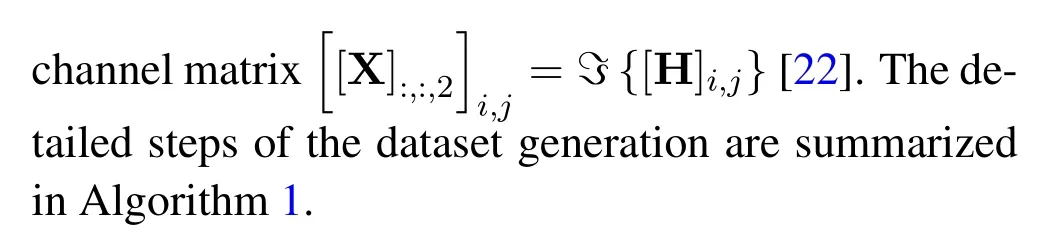
Algorithm 1.Dataset generation for PN.Input: SNR,Nt,Nr,NRFt ,NRFr Output:Dataset D 1:Initialize with t=1 and the dataset length is T =NS 2:for 1 ≤n ≤N do 3:Generate channel matrices Hn according to(4)4:Calculate Φ using(11)5:Construction Virtual Channel G using(12)6:Construction matrix J 7:Calculate ΩH =P using(15)8:~Q=images/BZ_107_432_1032_456_1078.pngINRFr0images/BZ_107_637_1032_661_1078.png0Ω QJ 9:Fn =VΦ1 2 PJ 10:Wn = ~Qimages/BZ_107_517_1215_538_1260.png1:NRF r ,:images/BZ_107_728_1215_749_1260.png11:for 1 ≤s ≤S do 12:σ2 = 10τs 20 13:~H(n,s) ～CNimages/BZ_107_628_1401_649_1447.pngH(n,s),σ2images/BZ_107_831_1401_852_1447.pngH images/BZ_107_604_1460_625_1506.png 14:images/BZ_107_373_1460_395_1506.pngimages/BZ_107_395_1474_414_1519.pngX(n,s)images/BZ_107_528_1474_547_1519.png:,:,1images/BZ_107_971_1474_998_1519.pngimages/BZ_107_373_1555_395_1600.pngimages/BZ_107_395_1568_414_1614.pngX(n,s)images/BZ_107_528_1568_547_1614.png:,:,2 images/BZ_107_604_1555_625_1600.png i,j =ℜimages/BZ_107_765_1474_792_1519.png[H(n,s)]i,j 15:i,j =ℑimages/BZ_107_765_1568_792_1614.png[H(n,s)]i,jimages/BZ_107_971_1568_998_1614.png16:Construct the data pair D(Xt,Ft,Wt)17:t ←t+1 18:end for 19:end for

IV.MTL FOR HYBRID PRECODING DESIGN

In this section,we present our DL framework for hybrid precoding design,which takes into account the power constraints and practical hardware constraints of phase shifter.Then,we analyze the computational complexity of the proposed method.

4.1 PRECODING NETWORK DESIGN

A multi-task learning based hybrid precoding network(PN)is proposed in this section to solve the hybrid precoding and combiner design problem.The proposed network architecture is shown in Figure 2.The first layer is the input layer used for receiving the dataset with dimensionNr×Nt×2.In addition,the real part of the channel matrix is the first channel and the imaginary part is the second one.The input layer is followed by two convolutional layers to reduce the risk of overfitting,which are called the parameter sharing layers.In this structure,the model needs to find a representation that capturing all the tasks while minimizing the risk of overfitting in a single task and learn implicit relationships between various tasks.Each layer contains 32 filters with size 2×2,which can be learned automatically from the network.

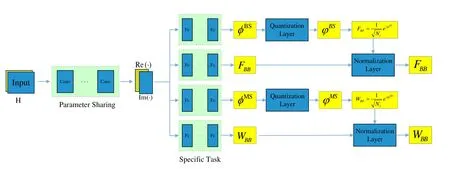
Figure 2.MTL based PN network.

The transmitting signals at the base station belong to the complex domain,we adopt the complex neural network that has a richer representational capacity.All of the fully connect and convolution operations are calculated in complex domain.Specifically,the complex filter matrix h = x+iy is convolved with the complex vector W = A+iB,where A and B are real matrices and x and y represent the real vector.Convolution operations in complex domains can be described as follows:

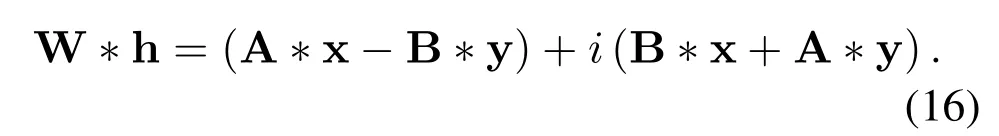
The description of complex convolution operations is illustrate in Figure 3.If we use matrix notation to represent real and imaginary part of the complex number,then the operations can be expressed as follows:

Figure 3.Complex convolution operations.

Figure 4.Illustration of the uniform quantization and Sigmoid quantization with B =3.

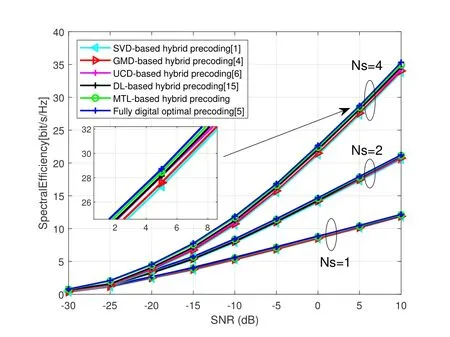
Figure 5.Spectrum efficiency of four precoding scheme versus the SNR .

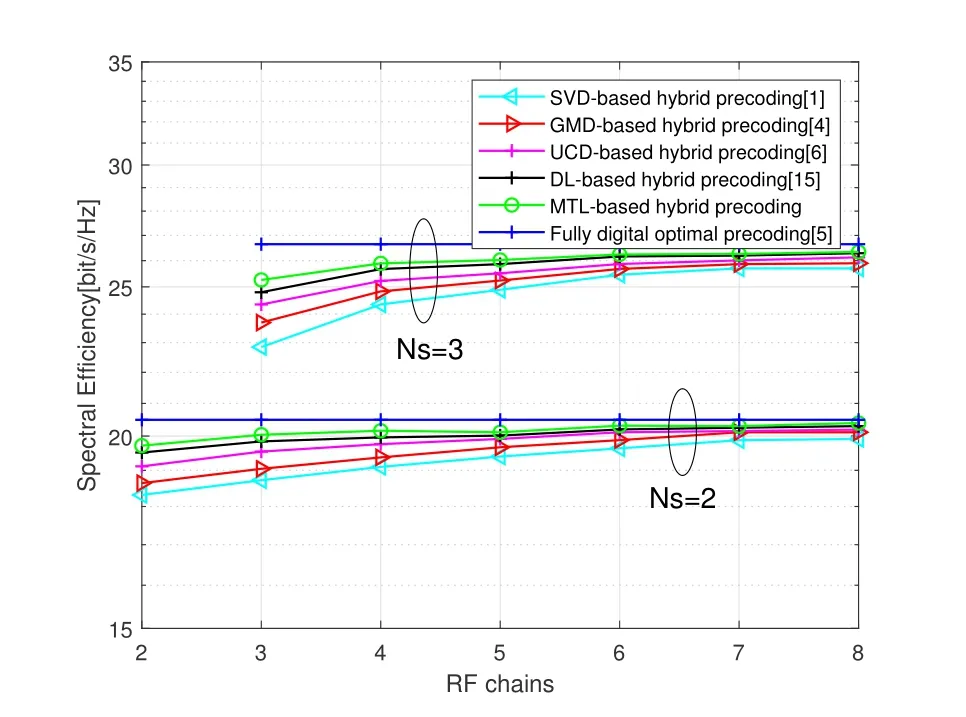
Figure 6.Spectrum efficiency versus the number of chains(Nt =256,Nr =8).

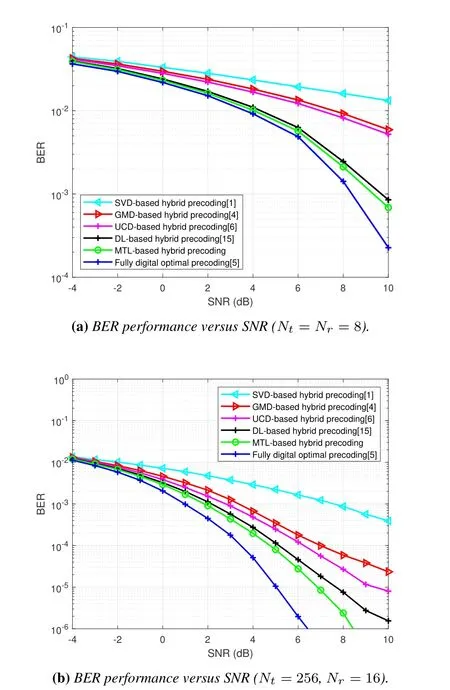
Figure 7.BER performance of four precoding scheme .

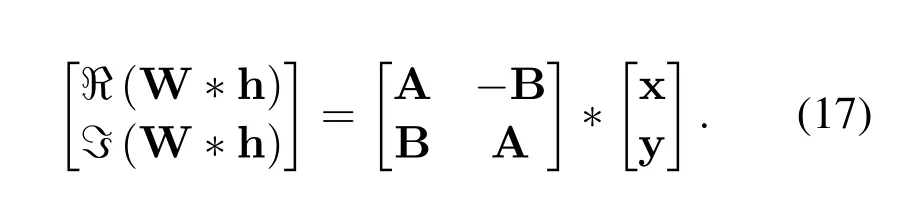
Then,four specific tasks are adopted to simultaneously design the hybrid precoding and combiner matrices.To avoid overfitting the model,several fully connected layers are used in each task,followed by a dropout layer with a probability of 0.5 random samplings.We use Leaky Rectified Linear Unit(Leaky ReLU)as the activation function,which can be described as follows:

wherebstand for constant,and we setb=100 in this paper.The number of units in each fully connected layer for each specific task is identical to the number of elements in the corresponding design matrix.And the number of units in each fully connected layer is

we customize the loss function to evaluate the prediction performance:

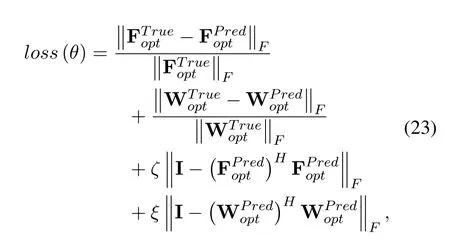
whereζandξrepresent the penalty coefficient.The purpose of the first two-term is to minimize the distance between the current output and the corresponding label,and the orthogonal features of Foptand Woptare satisfied by the last two.θis the parameters of the model and updated with the Adam optimizer[23].It should be noted that the analog precoder/combiner matrix and baseband precoder/combiner matrix are the outputs of the four specific tasks.We do not perform multiplication operations during the testing phase since the model does not perform back propogation during the testing phase.

In this paper,we set the number of convolutional layers and fully connected layers are both set to 3,ξ=ζ= 0.001.Training and test datasets contain 100,000,and 2,000 channel matrices,respectively.The level of noise that was added into channel matrix defined asSNR ∈{2,4,6,8,10}dB.During the training stage,the end-to-end training is used and the epoch number is 1000,the batch size is 64 and the learning rate is 0.0001.

4.2 COMPLEXITY ANALYSIS

V.NUMERICAL RESULT

Figure 6 shows the spectrum efficiency versus the number of RF chains whenSNR= 8dB.The figure illustrates that spectral efficiency improved when the number of RF chains increase.Meanwhile,the MTL based hybrid precoding scheme has only a negligible gap between the fully digital optimal precoding,while significant improvement than the other four hybrid precoding schemes.It is worth noting that the performance of the proposed method are still relatively robust to RF chains while the performance of the hybrid UCD improves with the amount of RF chains and the figure shows that the MTL-baed hybrid precoding algorithm is much more suitable in less RF chains than the hybrid precoding algorithm based on UCD.

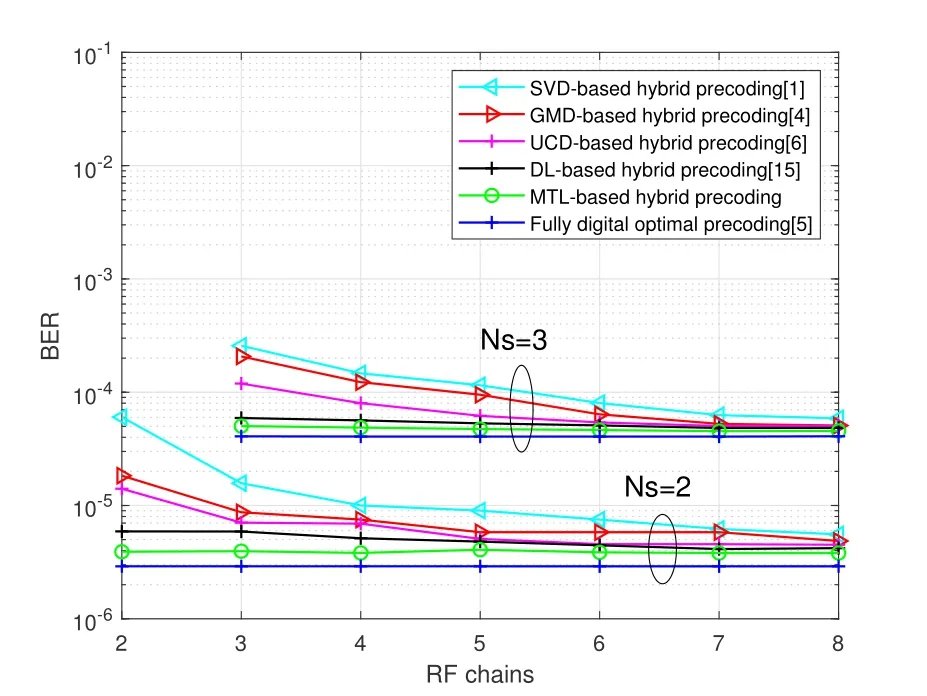
Figure 8.BER performance versus the number of chains(Nt =256,Nr =144).

Figure 7 shows the BER versus SNR plots under different antenna array sizes withNs= 2.Figure 7(a)shows that the BER of the MTL based precoding scheme outperforms the UCD and GMD based precoding algorithm in 8×8 massive mmWave system.At lower SNR,the performance of each scheme is similar while the gap between the MTL based hybrid precoding and GMD based hybrid precoding is obvious with increase of SNR.WhenBER= 10－2,the proposed MTL-based algorithm improve0.3dB,3dB,and 3.5dBcompared to DL-based algorithm,UCD-based algorithm and GMD-based algorithm respectively.To explore BER in larger antennas arrays,Figure 7(b)shows the BER performance in 256×16 mmWave systems withchains.With the antenna array size increase,the gap between MTL based hybrid precoding and DL-based hybrid precoding is getting large,which indicates that the MTL based hybrid precoding successfully eliminates the residual inter-stream interference.Although the performance of MTL based hybrid precoding inNr=Nt=8 is similar with fully digital optimal precoding,the performance gap is still obvious in largescale antenna arrays.

In Figure 8,the BER performance versus the number of chains is evaluated in a 256×144 mmWave systems withSNR=0dBandNs=2 or 3.It can be seen that with the increase of the number of RF chains,the BER of UCD based hybrid precoding decreases while the MTL-based hybrid precoding method remains unchanged.This indicating that the stability of the MTL-based method is relatively strong.Therefore,the proposed method is still optimal in terms of system configuration with fewer RF chains,and is more stable than the DL and UCD methods

VI.CONCLUSION

In this paper,we proposed a multi-task learning based precoding network model to jointly design hybrid precoding and combiner in mmWave massive MIMO systems.The computational complexity of the hybrid precoding algorithm based on multi-task learning is reduction.And the proposed method is compared with the SVD and GMD based hybrid precoding scheme.The simulation results show that in the case of imperfect CSI,better performance can be achieved in terms of bit error rate and spectral efficiency.

ACKNOWLEDGEMENT

This work was supported by the National Natural Science Foundation of China under grant No.61379028 and No.61671483;The Natural Science Foundation of Hubei province under grant No.2016CFA089;The Fundamental Research Funds for the Central Universities,South-central University for Nationalities under grant NO.CZY19003