Gridless Variational Bayesian Inference of Line Spectral from Quantized Samples

Jiang Zhu,Qi Zhang,Xiangming Meng

1 The Engineering Research Center of Oceanic Sensing Technology and Equipment,Ministry of Education,Zhoushan 316021,China

2 Ocean College,Zhejiang University,Zhoushan 316021,China

3 Institute for Physics of Intelligence,Graduate School of Science,The University of Tokyo,7-3-1,Hongo,Tokyo 113-0033,Japan

Abstract:Efficient estimation of line spectral from quantized samples is of significant importance in information theory and signal processing,e.g.,channel estimation in energy efficient massive MIMO systems and direction of arrival estimation.The goal of this paper is to recover the line spectral as well as its corresponding parameters including the model order,frequencies and amplitudes from heavily quantized samples.To this end,we propose an efficient gridless Bayesian algorithm named VALSE-EP,which is a combination of the high resolution and low complexity gridless variational line spectral estimation(VALSE)and expectation propagation(EP).The basic idea of VALSE-EP is to iteratively approximate the challenging quantized model of line spectral estimation as a sequence of simple pseudo unquantized models,where VALSE is applied.Moreover,to obtain a benchmark of the performance of the proposed algorithm,the Cram´er Rao bound(CRB)is derived.Finally,numerical experiments on both synthetic and real data are performed,demonstrating the near CRB performance of the proposed VALSE-EP for line spectral estimation from quantized samples.

Keywords:variational Bayesian inference;expectation propagation;quantization;line spectral estimation;mmse;gridless

I.INTRODUCTION

Line spectral estimation(LSE)is a fundamental problem in information theory and statistical signal processing which has widespread applications,e.g.,channel estimation,direction of arrival(DOA)estimation.To address this problem,on one hand,many classical methods have been proposed,such as the fast Fourier transform(FFT)based periodogram,subspace based MUSIC and ESPRIT[1].On the other hand,to exploit the frequency sparsity of the line spectral signal,compressed sensing(CS)based methods have been proposed to estimate frequencies for multiple sinusoids.Depending on the model adopted,CS based methods for LSE can be classified into three categories,namely,on-grid,off-grid and gridless,which also correspond to the chronological order in which they have been developed[2].At first,on-grid methods where the continuous frequency is discretized into a finite set of grid points are proposed.Grid based methods will incur basis mismatch when the true frequencies do not lie exactly on the grid[3].Then,off-grid compressed sensing methods have been proposed.In[4],a Newtonalized orthogonal matching pursuit(NOMP)method is proposed,where a Newton step and feedback are utilized to refine the frequency estimates.Compared to the incremental step in updating the frequencies in NOMP,the iterative reweighted approach(IRA)[5]estimates the frequencies in parallel,which improves the estimation accuracy at the cost of increasing complexity.In[6],a sparse Bayesian learning method is proposed,where the Newton method is applied to refine the frequency estimates.To completely overcome the grid mismatch problem,gridless based methods have been proposed[7].The atomic norm-based methods involve solving a semidefinite programming(SDP)problem,whose computation complexity is prohibitively high for large problem size.In[8],a gridless variational line spectral estimation(VALSE)algorithm is proposed,where posterior probability density function(PDF)of the frequency is provided.Later,multisnapshot VALSE(MVALSE)is developed for the multiple measurement vectors(MMVs)setting[9].

In practice,the measurements might be obtained in a nonlinear way,either preferably or inevitably.For example,in the mmWave multiple input multiple output(MIMO)system,since the mmWave accompanies large bandwidths,the cost and power consumption are huge due to high precision(e.g.,10-12 bits)analogto-digital converters(ADCs)[10].Consequently,low precision ADCs(often 1-3 bits)are adopted to alleviate the ADC bottleneck.Another motivation is wideband spectrum sensing in bandwidth-constrained wireless networks[11].In order to reduce the communication overhead,the sensors quantize their measurements into a single bit,and the spectrum is estimated from the heavily quantized measurements at the fusion center(FC).There are also various scenarios where measurements are inevitably obtained nonlinearly such as phase retrieval.As a result,it is of great significance in designing efficient nonlinear LSE algorithms.This paper will consider in particular LSE from low precision quantized observations but extension to general nonlinear scenarios could easily fit into our proposed framework without much difficulty.

1.1 Related Work

Many classical methods have been extended to solve the LSE from quantized samples.In[12],the spectrum of the one-bit data is analyzed,which consists of plentiful harmonics.It shows that under low signal to noise ratio(SNR)scenario,the amplitudes of the higher order harmonics are much smaller than that of the fundamental frequency,thus the classical FFT based method still works well for the SAR imaging experiment.However,the FFT based method can overestimate the model order(number of spectrums)in the high SNR scenario.As a consequence,the quantization effects must be taken into consideration.The CS based methods have been proposed to solve the LSE from quantized samples,which can also be classified into on-grid,off-grid and gridless methods.

·on-grid methods:The on-grid methods can be classified intol1minimization based approach[13,14]and generalized sparse Bayesian learning(Gr-SBL)[15]algorithm.Forl1minimization approach,the regularization parameter is hard to determine the tradeoff between the fitting error and the sparsity.While the reconstruction accuracy of the Gr-SBL is high,its computation complexity is high since it involves a matrix inversion in each iteration.

·off-grid methods:The SVM based[16]and 1bRelax algorithm[17]are two typical approaches.For the SVM based approach,the model order needs to be knowna priori,while the 1bRelax algorithm[18]gets rid of such need by using the consistent Bayesian information criterion(BIC)to determine the model order.

·gridless methods:The gridless approach can completely overcome the grid mismatch problem and the atomic norm minimization approach has been proposed[19,20].However,its computational complexity is high as it involves solving a SDP.

From the point of view of CS,many Bayesian algorithms have been developed,such as sparse Bayesian learning(SBL)[21],approximate message passing(AMP)[22]and vector AMP(VAMP)[23].Though LSE in essence is one nonlinear problem,by discretizing the range[-π,π)into a finite set(grid)of samples,it can be approximated as a linear inverse problem and thus the Bayesian techniques for compressed sensing can be applied,even for the quantized data case[24—26].The gridless variational Bayesian methods that work directly with continuously parameterized dictionaries to alleviate the model mismatch issues are also proposed,e.g.,[27].However,similar to classical ML frequency estimation methods,these variational Bayesian approaches[27]only compute point estimates of the frequencies in each iteration[27].In[8],the VALSE was proposed as a fully Bayesian approach which treats the frequencies as random variables and estimates their PDFs instead of point estimates.It has been shown that accounting for the uncertainty of frequency estimates benefits the model order estimation.Compared to the traditional techniques,this paper adopts the VALSE approach by treating the frequencies as random variables and estimating their PDFs from heavily quantized data.

In[28],a unified Bayesian inference framework for the generalized linear models(GLM)inference is proposed,which shows that GLM could be iteratively approximated as a(pseudo)standard linear model(SLM)using expectation propagation(EP)[29].This unified framework provides new insights into some existing algorithms,as elucidated by a concise derivation of generalized AMP(GAMP)in[28],and motivates the design of new algorithms such as the generalized SBL(Gr-SBL)algorithm[28,15].This paper extends the idea further and utilize EP to solve LSE from quantized samples.

1.2 Main Contributions

This work studies the LSE problem from quantized measurements and our goal is to design a lowcomplexity and high-resolution gridless algorithm to accurately estimate the line spectrum even in the case of coarsely quantized samples.The main contribution is to propose an efficient high-resolution gridless algorithm termed as VALSE-EP to address the LSE problem from coarsely quantized measurements.Compared to the unquantized case,the quantized samples consist of plentiful harmonics espically at high SNRs,which hinders the use of unquantized algorithms such as VALSE[8]since they will overestimate the model order.To suppress the harmonics and estimate the model order correctly,the proposed VALSE-EP takes into account the quantization effect by combining VALSE with EP[29]such that the quantized observation model is iteratively decoupled into a pseudo linear model.Numerical experiments on both synthetic and real data demonstrate the excellent performance of VALSE-EP.Furthermore,the relation between VALSE-EP and VALSE in the unquantized scenario is revealed.Given that VALSE-EP estimates the noise variance in the pseudo unquantized module,VALSE-EP is consistent with VALSE.

1.3 Paper Organization and Notation

The rest of this paper is organized as below.Section II describes the system model and introduces the probabilistic formulation.Section III derives the Cram´er Rao bound(CRB).The VALSE-EP algorithm and the details of the updating expressions are presented in Section IV.Substantial numerical experiments are provided in Section V and Section VI concludes the paper.

II.PROBLEM SETUP

The problem of LSE from quantized samples is formulated as follows.Letdenote a line spectra consisting ofKcomplex sinusoids

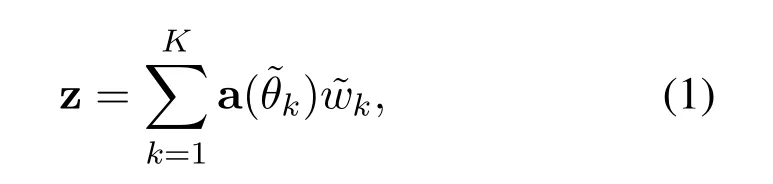
III.CRAM´ER RAO BOUND

IV.VALSE-EP ALGORITHM

In this section,the VALSE-EP algorithm is developed based on EP[29].According to EP and the factor

Figure 1.Factor graph of the joint PDF(10),the module of the VALSE-EP algorithm and the factor graph of the joint PDF(41).Here the circle denotes the variable node,the square denotes the factor node,and the dashed square denotes the pseudo factor node..According to the dashed block diagram in figure 1(a),the problem can be decomposed as two modules in figure 1(b),where module A corresponds to the standard linear model with factor graph shown in figure 1(c),and module B corresponds to the componentwise MMSE estimation.Intuitively,the problem can be solved by iterating between the two modules,where module A performs a variant of VALSE algorithm,and module B performs the componentwise MMSE estimation.

4.1 Componentwise MMSE Module

4.2 VALSE Module

4.2.3 Estimating the Model Parameters

4.3 From VALSE Module to MMSE Module

and we input them to module B.The algorithm iterates until convergence or the maximum number of iterations is reached.The VALSE-EP algorithm is summarized as Algorithm 1.

4.4 Initialization

Algorithm 1.VALSE-EP algorithm.1:Set the number of iterations T and implement the initialization in Subsection 4.4.2:for t=1,···,T do 3:Update J(54a)and h(54b)using ~y(t)and~σ2(t).4:Update ˆs, ˆwˆS and ˆCˆS(Section 4.2.2).5:Update ˆρ,ˆτ(60)(Section 4.2.3).6:Update ηi and ˆai for all i ∈ˆS(Section 4.2.1).7:Calculate the posterior means zpostA(t)(63)and variances vpost A(t)(64).8:Compute the extrinsic mean and variance of z as vext A(t)(67),zextA(t)(68).9:Compute the post mean and variance of z as zpost B(t)(27),vpostB(t)(28).10:Compute the extrinsic mean and variance of z as zext B(t)(31b)and vextB(t)(31a),and set ~σ2(t+1)=vext B(t)and~y(t+1)=zextB(t).Implement EM to estimate the noise variance as σ2(t+1)(37).11:end for 12:Return ˆθ,ˆw,ˆz and ˆK.

4.5 Computation Complexity

From Algorithm 1,it can be seen that VALSEEP involves the componentwise MMSE operation and VALSE.LetTdenote the number of whole iterations.For the componentwise MMSE operation,the computation complexity isO(NˆK).As for the VALSE,the complexity per iteration is dominated by the two steps:the maximization of lnZ(s)and the approximations of the posterior PDFq(θi|y)by mixtures of von Mises PDFs.This work approximates the posterior PDFq(θi|y)by Heuristic 2 in[8,Algorithm 2].Thus the complexity of the two steps areO(NˆK3)andO(N2)[8].Therefore,the complexity of VALSE-EP isO((NˆK3+N2+NˆK)T),comparable to that of VALSE with computation complexityO((NˆK3+N2)T)if ˆKare the same for the two algorithms.We have found that VALSE can be implemented more efficiently.Note that the approximations of the posterior PDFq(θi|y)by mixtures of von Mises PDFs has been implemented in the initializations.During iteration,the approximations of the posterior PDFq(θi|y)by von Mises PDFs is implemented only through refinements of the previous estimates.As a result,the complexities of VALSE-EP and VALSE areO(N2+(NˆK3+NˆK)T)andO(N2+NˆK3T),respectively.

4.6 Relationship Between VALSE-EP and VALSE Under Unquantized Setting

Proposition 1 reveals that the noise variance estimates of both VALSE-EP and VALSE can be derived via the EM step.For the VALSE algorithm,the noise variance estimate of the EM step is performed in module A,while for VALSE-EP,the noise variance estimate of the EM step is performed in module B.Thus in general,VALSE-EP is not exactly equivalent to VALSE even in the unquantized setting.However,if the noise variance estimation step in VALSE-EP is performed in module A,then VALSE-EP and VALSE can be shown to be equivalent in the unquantized setting.Empirically we find that when the noise variance is estimated in module B instead of module A,VALSE-EP performs better in quantized setting,while for unquantized setting,VALSE-EP performs similarly.

V.NUMERICAL SIMULATION

In this section,numerical experiments are conducted to evaluate the performance of the proposed VALSEEP algorithm.In addition,for performance comparison in the quantized setting,the AQNM is adopted and yq(69)is directly input to the VALSE to perform estimation.Furthermore,VALSE-EP is also compared with VALSE in unquantized setting.

5.1 Simulation Setup

At first,an experiment is conducted to show the effectiveness of the proposed design,by comparing with the conventional fast Fourier transform(FFT)and generalized parse Bayesian learning(Gr-SBL),and VALSE schemes.The parameters are set as follows:N= 100,K= 2 and the true frequencies are.The results are shown in figure 2 for SNR = 0 dB and SNR = 40 dB.Note that both FFT and Gr-SBL are on-grid approaches and thus they suffer from grid mismatch.The number of grids is set asNg= 100 and the grid spacing is 2π/Ng= 0.0628.The frequencies that are closest toare[-1.0053,2.0106]T.The maximum number of iterations are set as 300 for Gr-SBL,VALSE and VALSE-EP.To make the results clear,only the normalized reconstructed amplitudes above 10 dB are plotted.For low SNR(SNR = 0dB)scenario in figure 2a,the number of frequencies estimated by FFT and Gr-SBL are 6 and 4,respectively.While both VALSE and VALSE-EP estimate the model order successfully,demonstrating the high resolution of VALSE based approaches.For high SNR(SNR = 40 dB)scenario in figure 2b,the number of frequencies estimated by FFT,Gr-SBL,VALSE are 3,4 and 4,respectively.While VALSE-EP estimate the model order successfully,which validates the proposed VALSE-EP algorithm.

In addition,the computational complexities of the approaches are compared as shown in Table 1.The running time averaged over 50 MC trials on a desktop computer with an Intel(R)Core(TM)i7-4790 3.60GHz CPU of the algorithms are evaluated.For both low and high SNR scenarios,FFT is the fastest.Besides,the running time of the proposed VALSE-EP is comparable to that of VALSE,and is lower than that of Gr-SBL.

For the ensuing subsections,three numerical experiments with synthetic data and one with real data are conducted to demonstrate the excellent performance of VALSE-EP under quantized setting,compared to VALSE.

5.2 Estimation Versus SNR

The performance of the VALSE-EP versus SNR is investigated and the results are plotted in figure 3.For the signal reconstruction and model order estimation probability,figure 3a and 3b show that for 1 bit and 2 bit quantization,as SNR increases,the performances of VALSE first improve,and then degrade,while the performances of VALSE-EP always improve and are better than VALSE.A surprising phenomenon is that VALSE-EP under 2 bit quantization achieves the highest success rate of model order estimation and approaches to the CRB firstly.As the SNR continuous to increase,VALSE-EP deviates a little away from CRB under 1 bit and 2 bit quantization,while in the unquantized setting,both VALSE and VALSE-EP approach to the CRB asymptotically.

5.3 Estimation versus Number of Spectral K

The performance of VALSE-EP is investigated with respect to the number of spectralK,and results are presented in figure 4.For the signal reconstruction error and success rate of model order estimation,the performances of all algorithms degrade asKincreases,except that VALSE under 1 bit quantization,which first improves and then degrades.For the frequency estimation error,asKincreases,VALSE degrades quickly and deviates far way from CRB whenK ≥4 under 1 bit quantization.WhenK ≤6,VALSE-EP is always close to the CRB under 1 bit quantization.AsKcontinues to increase,the frequency estimation error of VALSE-EP begin to deviate far way from CRB.

5.4 Real Data

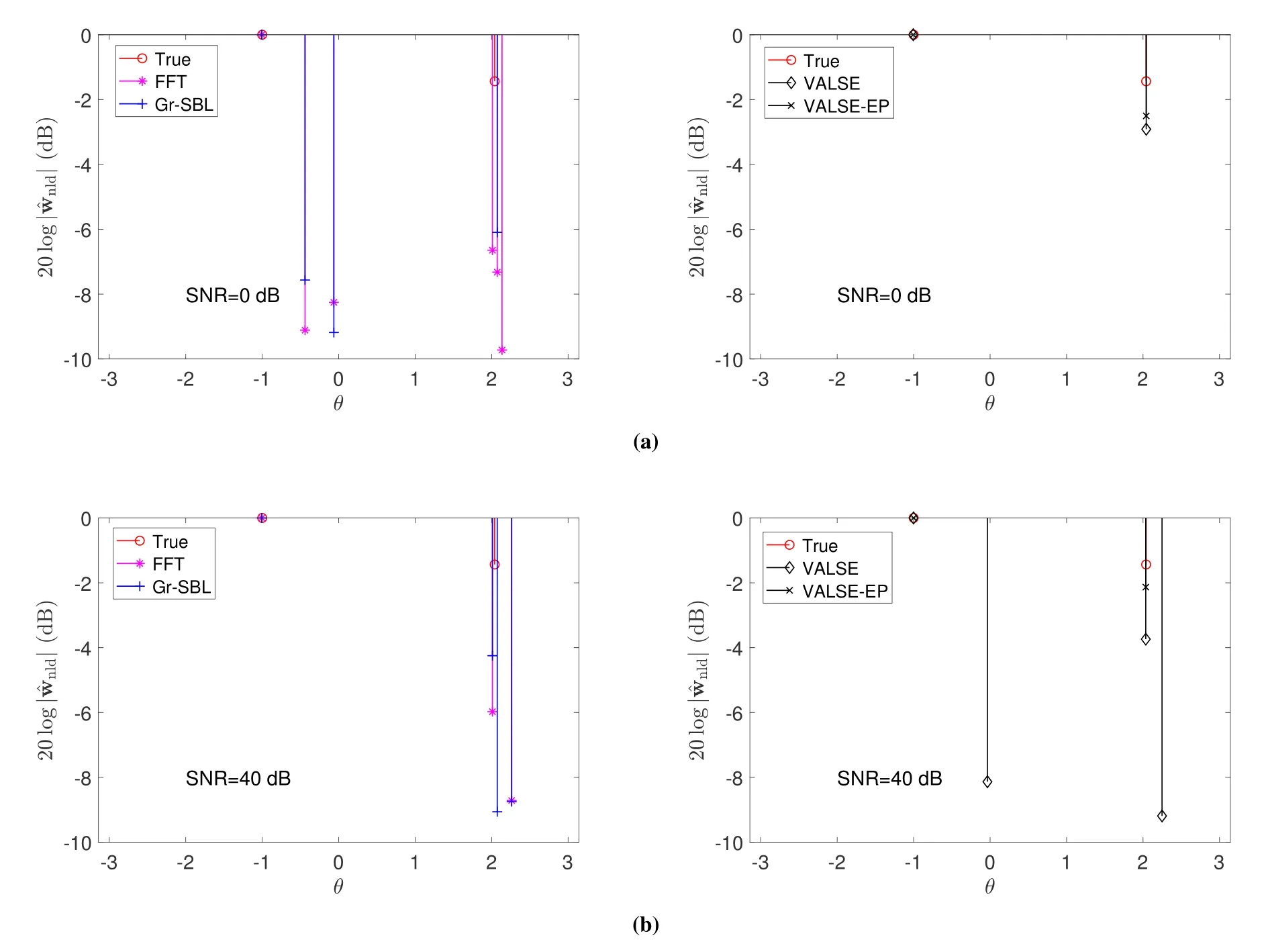
Figure 2.Typical reconstruction results of FFT,Gr-SBL,VALSE-EP and VALSE under 1 bit quantization at SNR = 0 dB and SNR=40 dB.The normalized amplitudes are plotted.

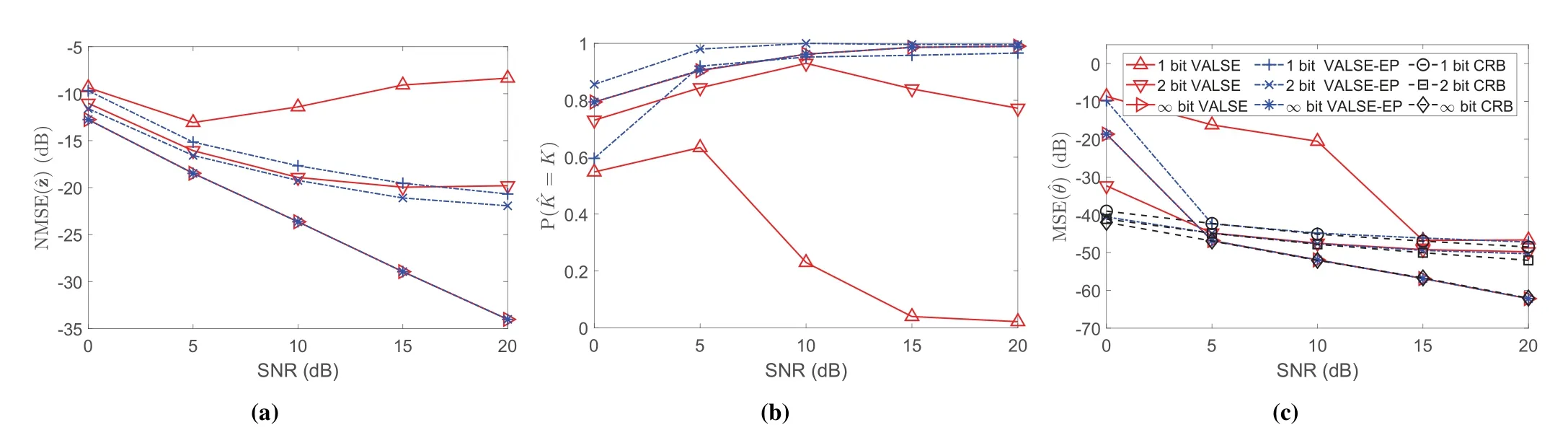
Figure 3.Performance versus SNR for N = 100 and K = 3:(a)NMSE of the reconstructed signal;(b)success rate of model order estimation;(3)MSE of frequency estimation.

VI.CONCLUSION

Figure 4.The performance of VALSE-EP versus the number of spectrum K for N =160 and SNR=10 dB.

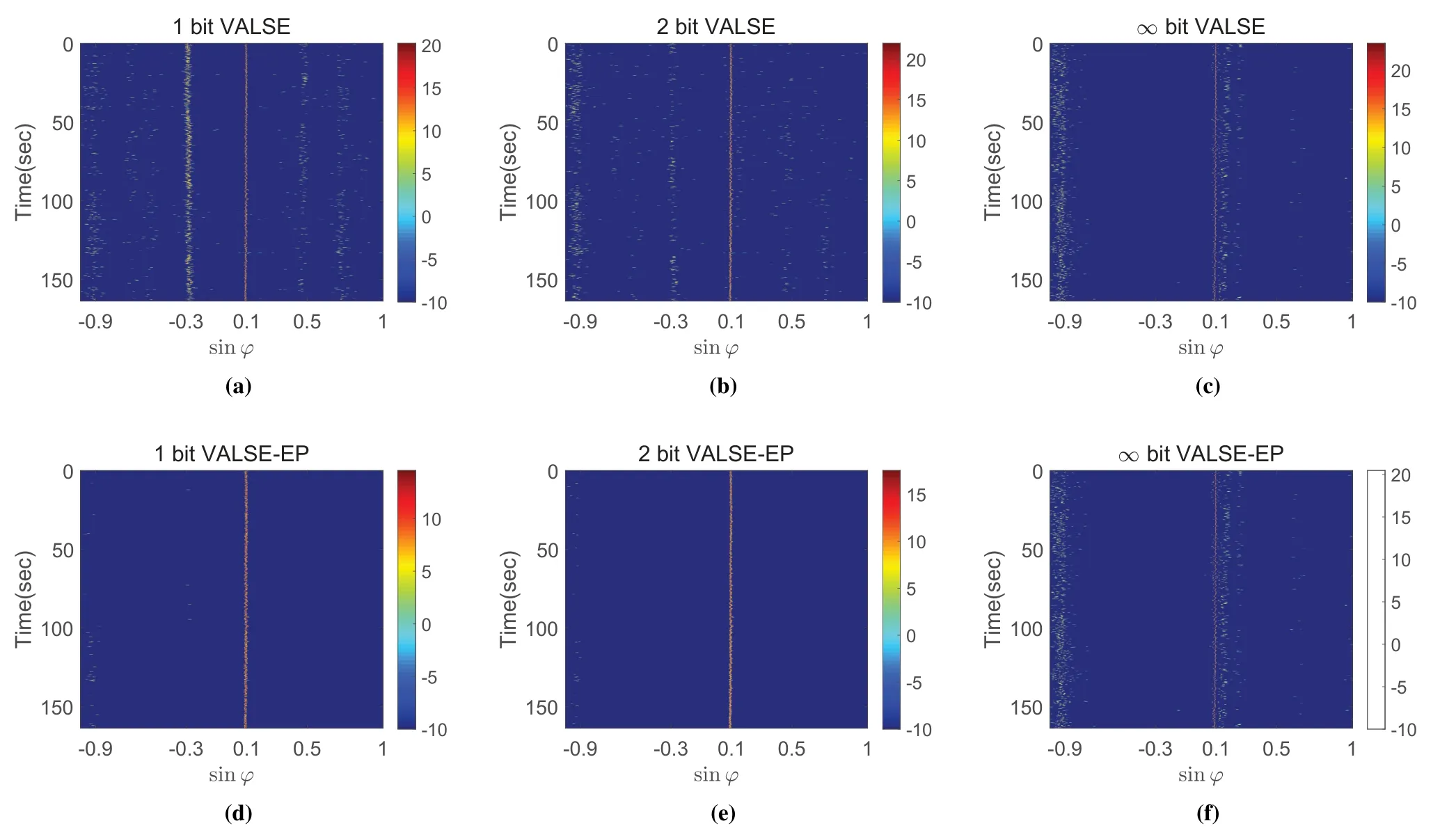
Figure 5.The synthesized posterior PDF of sin φ for real data.

In this paper,a VALSE-EP algorithm is proposed to deal with the fundamental LSE problem from quantized samples.The VALSE-EP is one kind of lowcomplexity gridless algorithm which iteratively refines the frequency estimates,automatically estimates the model order,and learns the parameters of the prior distribution and noise variance.Besides,VALSE-EP provides the uncertain degrees of the frequency estimates from quantized samples.Substantial numerical experiments are conducted to show the excellent performance of the VALSE-EP,including on a real data set.

ACKNOWLEDGEMENT

This work was supported by National Natural Science Foundation of China(No.61901415).

APPENDIX

Finding the Local Maximum of ln Z(s)

A greedy iterative search strategy similar to[8]is adopted to find a local maximum of lnZ(s).We proceed as follows:In thepth iteration,thekth test se-

Calculating the Post Variance (64)