Evolution and Effectiveness of Loss Functions in Generative Adversarial Networks

Ali Syed Saqlain,Fang Fang,*,Tanvir Ahmad,Liyun Wang,Zain-ul Abidin

1 School of Control and Computer Engineering,North China Electric Power University,Beijing 102206,China

2 Department of Computer Science,Portland State University,Portland 97207,U.S.

3 School of Information and Communication Engineering,South West Jiaotong University,Chengdu 610031,China

Abstract:Recently,the evolution of Generative Adversarial Networks(GANs)has embarked on a journey of revolutionizing the field of artificial and computational intelligence.To improve the generating ability of GANs,various loss functions are introduced to measure the degree of similarity between the samples generated by the generator and the real data samples,and the effectiveness of the loss functions in improving the generating ability of GANs.In this paper,we present a detailed survey for the loss functions used in GANs,and provide a critical analysis on the pros and cons of these loss functions.First,the basic theory of GANs along with the training mechanism are introduced.Then,the most commonly used loss functions in GANs are introduced and analyzed.Third,the experimental analyses and comparison of these loss functions are presented in different GAN architectures.Finally,several suggestions on choosing suitable loss functions for image synthesis tasks are given.

Keywords:loss functions;deep learning;machine learning;unsupervised learning;generative adversarial networks(GANs);image synthesis

I.INTRODUCTION

Generative Adversarial Networks(GANs)[1]recently proposed are a class of deep generative models that aim to learn the true data distribution by playing an adversarial zero-sum game between two players.A generator and a discriminator.As a data generator,the generator generates synthesized data signals to fool the discriminator by generating even more realistic data samples during training.While discriminator is trained to distinguish among real and generated data samples,the goal of a discriminator network is to,assign high probability values to the real data samples from the real data distribution.Meanwhile,it assigns low probability values to the generated fake data samples from the generator network.In a conventional generative adversarial model,both generator and discriminator networks play an adversarial role against each other until Nash equilibrium is achieved,that is,a generator network successfully learns to generate realistic samples which,a discriminator is unable to classify as fake.

Compared with other existing literature on generative modeling,such as,Variational Autoencoders[2],GANs layout a compact and efficient foundation for learning generative models.Since the introduction of GANs framework,GANs have been used in applications such as image editing[3—6],image translation[7—12],image super resolution[13—16],video prediction[17—19],and many other tasks[20—24].

Training GANs,however,is a challenging problem,it poses problems such as mode-collapse and vanishing gradient.Mode-collapse emerges when a generator network is unable to learn the multi modes of data and focuses only on learning a single data mode while ignoring all others,In that case a generator has failed to produce plausible samples which,represent the multi modes of the training data[25—29].Meanwhile,the vanishing gradient problem occurs when a generated data distribution generated by a generator and the target true data distribution do not coincide(normally at the beginning of training),which further explains,the discriminator network is too successful at rejecting generated samples with high confidence,providing no subtle gradient updates to the generator during training which results in,vanishing gradient and the generator learns nothing[30].

In addition,to alleviate the problems of modecollapse and vanishing gradient,recent research suggests both generator and discriminator networks to be deeper and larger.However,considering the weak nature of adversarial framework,it is hard to balance and optimize such deep networks to attain fast convergence and optimal solution.Thus,it is equally important to choose appropriate configurations for the network(e.g.,network learning rate,updating steps and network architecture).These settings play a crucial role in improving or reducing GANs performance.Inappropriate configurations may result in network failure or produce undesirable results.

A huge amount of recent research have been devoted to tackle the aforementioned problems by introducing different adversarial objective functions for training GANs.Assuming,the optimal discriminator network is learned for a given generator as in original GANs[1],since then various adversarial objective functions are proposed for a generator network that aim to measure distinct distributional distances between the generated data distribution and the target data distribution.The original GAN aims to measure Jensen-Shannon divergence between the generated and the target data distributions while,other such approaches include least-squares GANs[31],DCGANs[32](aim to measure Jensen-Shannon divergence in deep convolutional architecture),Earth-mover distance[33]and absolute deviation[34].The purpose of recent studies and introduction of different methods to improve GAN performance is to,minimize the distance between the generated and the target distributions.However,minimizing each distance comes with its own pros and cons.For example,minimizing Jensen-Shannon divergence is hard,which may result in vanishing gradient problem due to the network’s minimax nature.while minimizing KL divergence annihilates the vanishing gradient issue,but it fails to deal with modecollapse[32,25].Wasserstein distance WGAN[33]on the other hand,successfully eliminates the modecollapse issue by seeking to increase the gap between the scores of the real and the generated data.

However,through extensive experiments we find that GANs performance heavily depends on a careful selection of objective function,network architecture and its hyper parameters.Since the training strategy for GANs is particularly fixed,it is hard to maintain the equilibrium between a generator and a discriminator network during training while choosing a loss function that is less sensitive to the model architecture and its hyper-parameter configurations.

In this paper,we study the effects of loss function in GANs,its variants,and the evolution of different GAN models.We also study the performance of GANs in a single and multiple generator(multigenerator)discriminator architectures by performing a survey on different single and multi-generator networks in Sections III and IV.Despite the tremendous success of GANs in generative modeling which leads to generating high quality plausible samples.however as mentioned earlier GANs suffer from the major problem such as mode-collapse[26,27].In this paper,we mainly focus on the problem of mode collapse,and the appropriate loss functions.To address this issue many variants of GAN have been proposed which can be divided into two main categories:training either a network with a single generator or with multiple generators.the first method emphasises on modifying discriminator’s objective function[26,28],for generator’s objective function modification[35],and using more than one discriminator[36,37]to provide more stable gradients updates to a generator network.The second method includes multiple generators against a single or more than one discriminator[38,39]to cover all data modes.However,sequentially adding multiple generators to the network can be computationally expensive as Tolstikhinet al.[40]adds multiple generators by applying boosting techniques to train the mixture of generators.Moreover,this method implies that a single generator is able to generate plausible data samples of some data modes,so reassessing the training data and continue adding new generators will lead to a mixture of their distribution that covers all the data modes.This presumption is not true,since single-generator GANs trained on diverse image datasets such as ImageNet tends to generate poor results of unrecognizable objects.Training multiplegenerator GANs requires explicit mechanism to force multiple generators to learn different data modes simultaneously while,enforcing divergence among generators to generate plausible data samples of different data modes nonetheless,ensuring the high quality of generated samples.More recently,Goshet al.[38]and Hoanget al.[39]propose multi-generator GANs.The former approach trains multiple generators against a single multi-class discriminator that in addition,besides predicting whether a generated data sample is real or fake also classifies which generator generates the sample.However,this model directly penalizes generators for generating fake samples but it fails to encourage generators to cover different modes of data space.while the latter approach,trains many generators against a discriminator and a classifier,while maximizes the Jensen-Shannon(JSD)divergence among generators and minimizes the JSD between the mixture of distributions induced by generators and the true data distribution.However,this method partly solves the problem of mode collapse by employing JSD as objective function among generators and true data distribution but it struggles to generate high quality data samples on real world datasets since minimizing JSD between the mixture of generated distribution and the true data distribution is hard which in addition,causes vanishing gradient problem and compromises the quality of generated samples.

Meanwhile,in this paper we study the effects of different loss function in GANs,firstly in two-player GAN frameworks,where a single generator and discriminator networks play an adversarial game againt each other,and secondly in multi-generator discriminator networks where,multiple generators play an adversarial game against one or more than one discriminator.we also provide concrete analyses on the architectural evolution of GANs by providing a comprehensive overview of different GAN approaches,and the qualitative comparison of the generated samples on various datasets.The importance of our research is different than many other survey papers,in a sense our research studies the effects of different loss functions in GANs along with their pros and cons,and provides the comparison of two-player to multi-generator discriminator GANs.Besides analyzing different GAN models,we give an in detail introduction of some common problems posed by GANs,and the possible solutions to avoid these problems.At present there are many surveys on GANs[41—45],and these works have introduced and explained GANs in details in terms of recent algorithms,model structure of GANs,applications of different GAN approaches,and the limitations of GANs.However,considering the vast amount of recent research on GANs,some of the most frequent and common problems are partially unexplained and lack the intuition for such problems.Unlike these surveys,in this paper we explain such GAN related problems in depth,providing a strong intuition for both the novice and expert researchers in the field of GANs.

In summary,we make following contributions in this survey paper:

·We present in depth understanding of GANs,its theoretical background and training mechanism comprehensively.

·We discuss the most common problems posed by training GANs such as,mode-collapse and vanishing gradient in depth.

·We discuss various different GAN architectures from two player GANs to multi-generator discriminator networks along with their loss functions in detail.

·Not only we discuss pros and cons of these loss functions in different GAN frameworks,but we also perform qualitative and quantitative comparison of these loss functions on three large-scale image datasets.

·We provide suggestions on choosing a suitable loss function based on extensive study of existing literature and our own experimental analysis on different loss functions.

·Last but not least,we discuss the applications and future of GANs in various other promising fields besides vision-related tasks.

The rest of the paper is as follows.In Section II.we present the related work and comparative study of our survey with other existing surveys on GANs.Section III.presents the basic theory and background of GANs with its training mechanism.Section IV.presents various different adversarial loss functions in existing GAN approaches,and discusses pros and cons of these loss functions.Section V.presents the architectural evolution of GANs along with their loss functions in detail.In Section VI.we present the evaluation results of different loss functions in GANs based on evaluation metrics,and we provide various suggestions on selection of a loss function,also we discuss the applications and future of GANs in computer vision and various other promising fields.Finally,in Section VII.we draw conclusions for this survey paper.

II.RELATED WORK

In this section,we provide the comparative study between our survey paper and other existing surveys on generative adversarial networks.

2.1 Comparative Study

Recently,Wanget al.[41]provided an extensive study on the taxonomy of generative adversarial networks,and discussed the cause of most common problems in GANs such as,mode-collapse and vanishing gradient in detail.However,the authors do not discuss each loss function related to different GAN frameworks in detail,also their survey is based on the architectures,where a single generator and a discriminator play an adversarial role against each other while ignoring more than two or multi-generator and discriminator frameworks.The authors discuss the applications of GANs mostly related to vision related tasks and do not discuss their applications in promising fields such as,Blockchain,Big Data,and other IoT systems.

Panet al.[42]presented recent progress on generative adversarial networks and briefly discussed different GAN architectures,while the authors do not provide in-depth insights for the root cause of the problems faced by GANs.Their study lacks the sufficient literature on different loss functions in various GAN frameworks,and they do not provide comparative analyses on different GAN frameworks either qualitatively or quantitatively.

Wuet al.[43]presented a survey on image synthesis and editing tasks using generative adversarial networks.Similar to[42],the authors do not discuss the importance of loss functions in different GAN architectures,nor do they provide experimental details either qualitatively or quantitatively.Meanwhile,their study also excludes important discussion on the most common issues in GANs such as,mode-collapse and vanishing gradient.

Wanget al.[44]presented a general introduction of generative adversarial networks.Similar to the recent surveys on GANs[42,43],the authors do not include a detailed background for different loss functions and their importance in GANs,moreover,abstract discussion on different task-oriented GAN architectures is carried out without any experimental proof or analyses.

Hitawalaet al.[45]presented a brief survey on generative adversarial networks.The authors only focused on discussing few GAN variants related to the conditional-GANs(cGAN)[46]while disregarding important aspects of various loss functions and optimization techniques in generative adversarial networks.

All these existing surveys on GANs[41—45]either fail to discuss loss functions of GANs and different GAN architectures in depth,or do not provide experimental results to support the theoretical understanding of GANs,and the problems posed by the adversarial nature of GANs.However,among all these existing surveys,we consider[41]to be more detailed in content related to different GAN frameworks and their loss functions yet the authors of the survey do not consider including multi-generator and discriminator GAN frameworks in the literature,nor do they introduce emerging optimization methods for stabilizing the GANs training process such as utilizing evolutionary computation(E-GAN)[47]for solving modecollapse and vanishing gradient problem.While,we present a detailed survey that not only discusses loss functions of GANs in two-player architectures but we also extend our study to multi-generator and discriminator networks.Besides that,we also discuss emerging optimization methods such as,evolutionary algorithms(E-GAN)[47]for vanishing gradient and mode-collapse issues.Meanwhile,we discuss the applications of GANs in promising fields such as,Blockchain,Big Data,and other IoT systems.We do not claim our survey on GANs to be perfect,since our goal is not directed towards achieving perfection.However,we aim to provide a more generalized and in-depth overview of different GAN architectures and their loss functions with enough experimental support both qualitatively and quantitatively.In Section III we discuss the theoretical understanding behind GANs and the training procedure.

III.GENERATIVE ADVERSARIAL NETWORKS

In this section we present the theoretical background of Generative adversarial networks and its training mechanism.

3.1 Theory Behind GANs

Generative Adversarial Networks(GANs)follow the idea of game theory by defining a zero-sum between two competing neural networks.The generator network takes an input noise vector and generates fake data to fool the discriminator.The discriminator network receives the real data along with the fake batch of data generated by generator and calculates the loss between fake and real data samples which is then back propagated to the generator network.

Conventionally,the objective function for the generator and the discriminator is defined as the minimax objective,

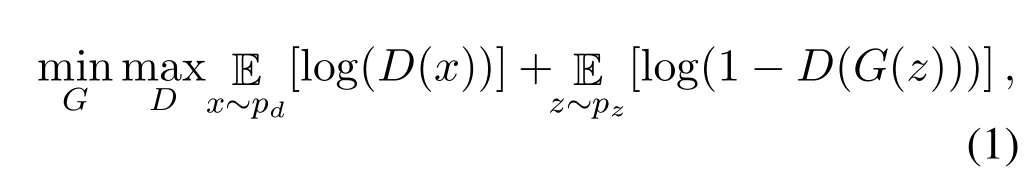
wherexrepresents the real data sample from the real data distributionpd,zrepresents the random uniform noise vector as an input to the generatorGwhilepzrepresents the generated data distribution generated by the generatorG.D(x)is the probability that the samplexcame from the real data distribution,D(G(z))represents the probability of generated data distribution by the generatorG.For the generatorG,in order to to fool the discriminatorD,the probabilityD(G(z))needs to be maximized for the generated data,so that log(1-D(G(z)))is minimized.For the discriminator networkD,binary cross entropy function is utilized to distinguish between the generatedsampleG(z)and the real data samplex,the goal for the discriminator in Equation.(1)is to maximize the probability of a generated sample to be discriminated as fake.Figure 1 represents the architecture of conventional GANs with an input latent vactorzto generator network,and the output of the generator is classified as fake or real by the discriminator network.While Table 1 represents the most commonly used symbols and notations,which we will use in following sections describing different loss functions of GANs.

Table 1.Most commonly used symbols and notations.

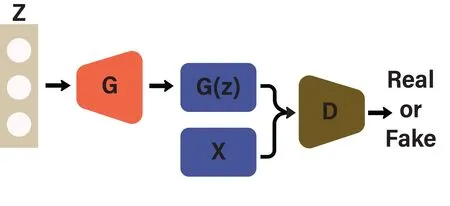
Figure 1.The architecture of generative adversarial networks.

Table 2.Classification of adversarial loss functions in GANs.

3.2 Training Procedure

Simultaneously training generatorGand discriminatorDcan be a difficult task for the training network,so in practiceGis held fixed firstly,and the parameters ofDare updated over some certain number of training iterations to improve the performance and the accuracy of discriminatorD.After the optimization ofD,the training parameters of generatorGare optimized whileDis held fixed[1].The discriminatorDcan only be optimal for a given generator only if.After several training steps,ifGandDhave enough capacity,both adversaries will be optimized in such a fashion that they will reach Nash equilibrium.At this point bothGandDcannot improve any further because the generated distributionpz=pd(x).The discriminator can no longer differentiate between the generated distribution and the real data distribution,i.e..The nature of objective function used in conventional GANs is equivalent to minimizing Jensen-Shannon divergence(JSD)as mentioned earlier.However JSD as a loss function for regular GANs poses major problems for the network optimization,it suffers from mode-collapse which is,still an active research area while optimizing the performance of GANs.

To summarize this section,we discussed the theoretical background for GANs and we also discussed the basic training procedure in GAN framework.In the next section,we present the effectiveness of different loss functions in generative adversarial networks in detail.

IV.LOSS EFFECTIVENESS IN GENERATIVE ADVERSARIAL NETWORKS

In the previous section,we discussed the idea behind GANs and its training procedure.We also mentioned that the original GANs objective is equivalent to minimizing JSD between generated distributionpz(x)and real data distributionpd(x).However,considering the fact that there are number of generative adversarial networks,that aim to improve the loss function performance in GANs by proposing new loss functions and loss optimization techniques.In this section we discuss some notable loss functions recently proposed for GANs,their problems and optimization techniques in detail.

4.1 Recent Adversarial-based Loss Functions in GANs

Regular GANs[1]have some common number of failure modes,such as mode-collapse and vanishing gradient caused by minimizing JSD between the generated and the true data distributions.While none of these problems have been completely resolved,they are still an active research area.To solve these problems,we divide loss functions into the categories such as:divergence-based loss functions,divergence to Wasserstein loss,and from Wassserstein to other loss optimization methods.Table 2 presents the classification of different adversarial loss functions used in GANs among which,the most commonly used loss functions are the divergence-bases loss functions,and the family of Wasserstein loss functions.

4.2 Divergence-based Loss Functions

The divergence-based loss functions[52,53]is a common term for all types of well known divergences including JSD that are used to address the most commonfailure modes in GANs,the most commonly used divergence for GANs are given in Table 3.The functionDf(P ‖Q)is basically used to measure the difference between two probability distributionsPandQ.For a convex functionf,if the two probability distributionsPandQare absolutely continuous over a space Ω then the divergence between two probability distributions can be defined as,

Table 3.Some commonly used divergence-based objective functions in GAN.

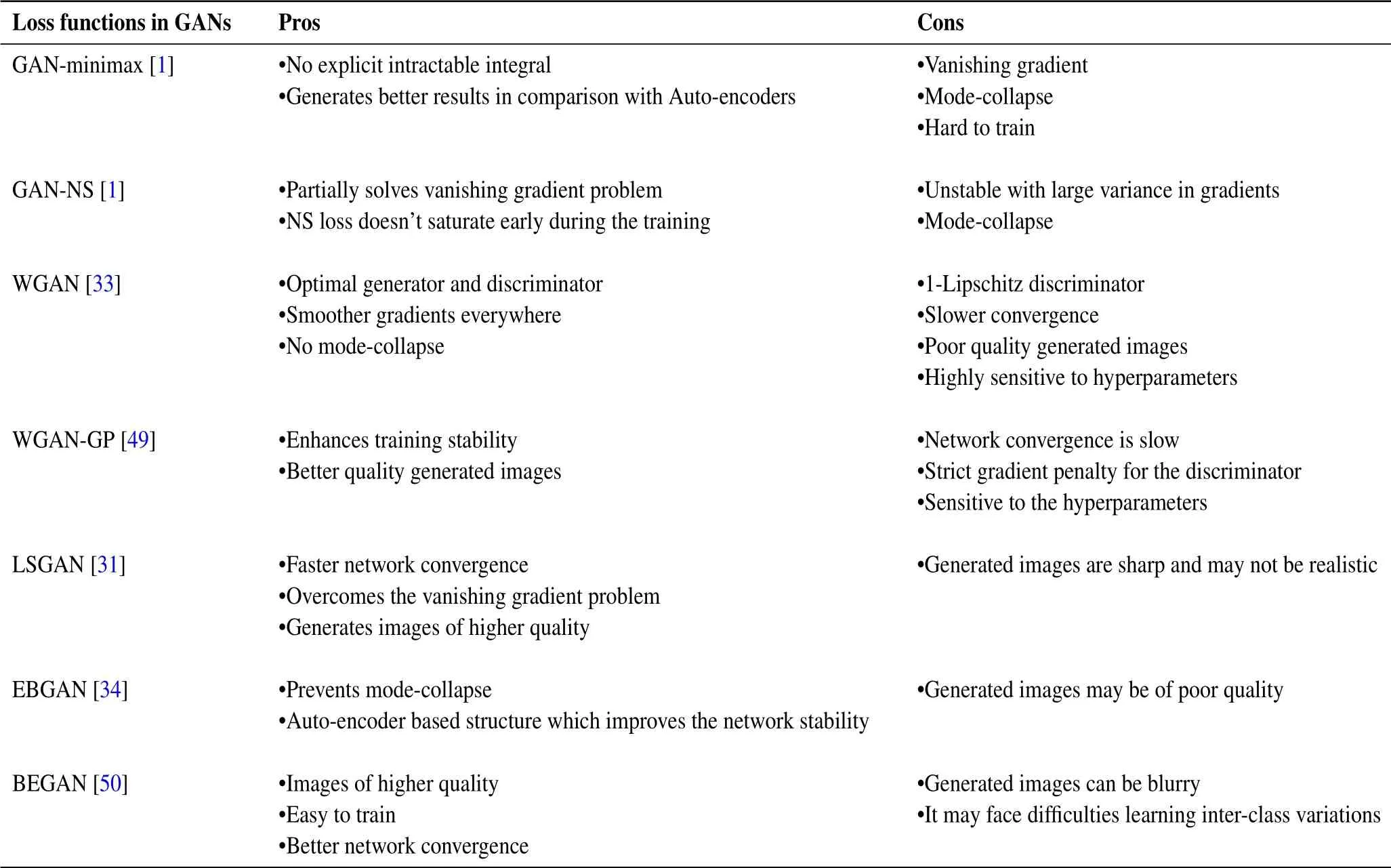
Table 4.Pros and cons of different GAN approaches.

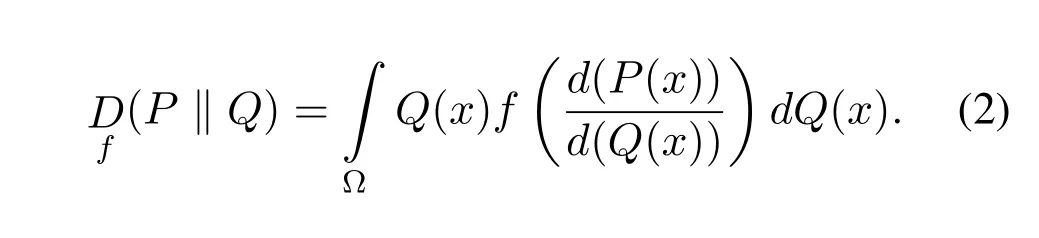
In a case,whereP(x)=Q(x)for∀x,the divergence between the two probability distributions will approach to 0.At this moment in time,there is no difference between the probability distributionsPandQ,which can be defined as,

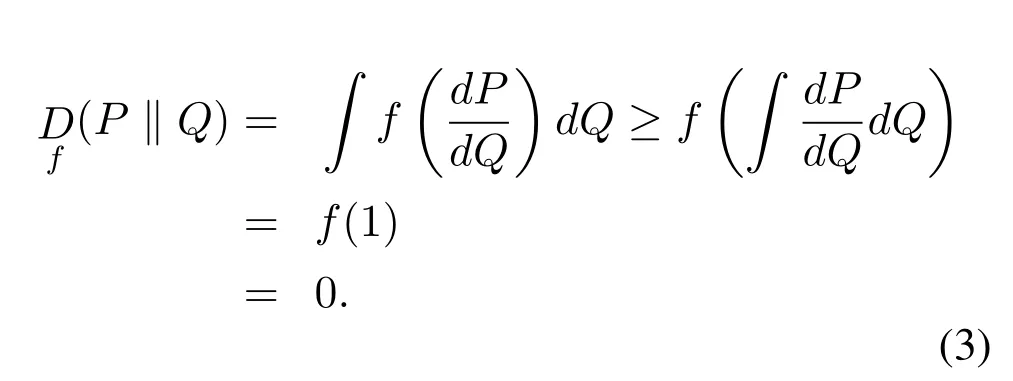
Equation(3)can also be expressed as Jenseninequality.Given the condition that the divergence between two absolutely continuous probability distributions can approach 0 only ifP(x)=Q(x),we can define the general form of divergence-based loss as,

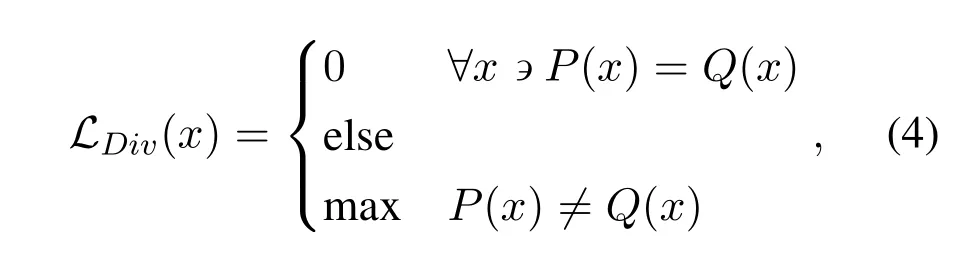
whereLDiv(x)in Equation(4)is a general form of divergence-based loss function.It is 0 when two probability distributions coincide and there is no difference between the two distributions,otherwise it is maximum when the two distributions are not similar.

Least-square GAN.Sigmoid cross entropy loss was proposed for the discriminator network in the original GANs and introduced two distinct loss functions for the generator network,the first one is known as the minimax loss function while the second is the non-saturating loss function.However due to the saturating properties of minimax loss in the early stages of the learning process,it is recommended to use nonsaturating loss function in practice.

Maoet al.(LSGANs)[31]argued that optimizing both the non-saturating loss-log(D(G(z))and minimax loss in Eq.(1)lead to the problem of vanishing gradients during the generator updates.To alleviate the problem of vanishing gradients,Maoet al.[31]proposed a least-square loss function based on Pearsonχ2divergence for both the generator and discriminator.The proposed least-square loss provides two advantages over using non-saturating loss(NS)and the minimax loss.First,LSGANs generate the images of higher quality.Second,LSGANs have proven to be more stable during training.The least-square GAN objective functions for the discriminator and the generator are the squared error,defined in Equations(5)and(6).

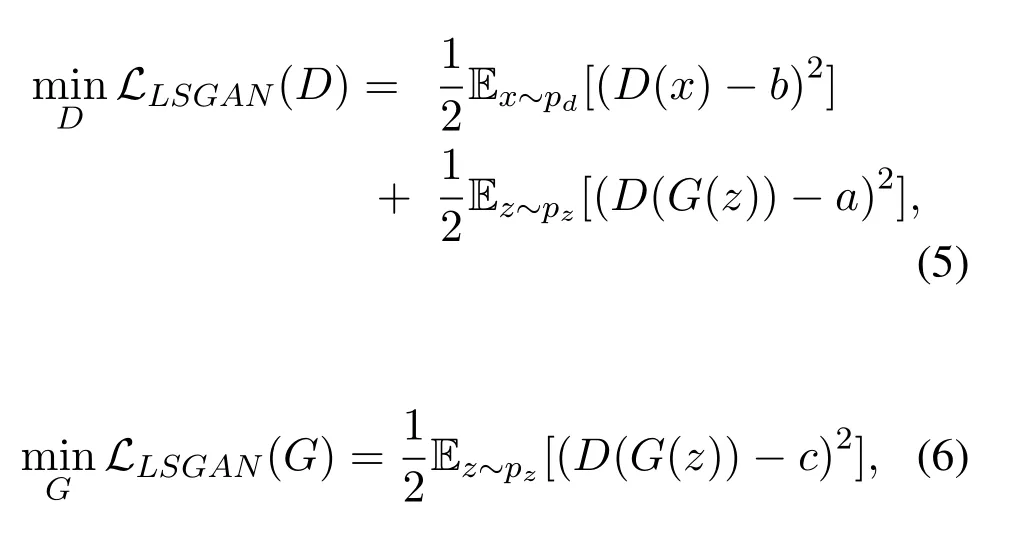
whereaandbrepresent the labels of generated and real data,respectively.For a given generatorG,thegoal of discriminatorDis to minimize the objective function in LSGANs.Whereas,cindicates the value for whichDis fooled to believe that the fake sample generated byGis real.

Unlike the non-saturating loss(NS)and the minimax loss,the loss function of LSGANs penalizes the fake samples that are far from the decision boundary,even though if the discriminatorDis successful at classifying the fake samples correctly,the reason behind penalizing the fake samples that are correctly classified is to tackle the problem of vanishing gradients which causes no gradient updates for the generatorG,pros and cons of different GANs and their loss functions are explained in Table 4.Another advantage of penalizing the fake samples encouragesGto generate more realistic looking samples toward the decision boundary,thus pushing the generatorGto learn to generate samples as close to as real data manifold.LSGANs prove the fact that minimizing Pearsonχ2divergence as compared to JSD,leads to the network training stability during training,and prevents the objective function from getting saturated.

KL and Reverse KL divergence.Kullback-Leibler(KL)divergence measures the difference of divergence between two probability distributionsPandQdefined as,

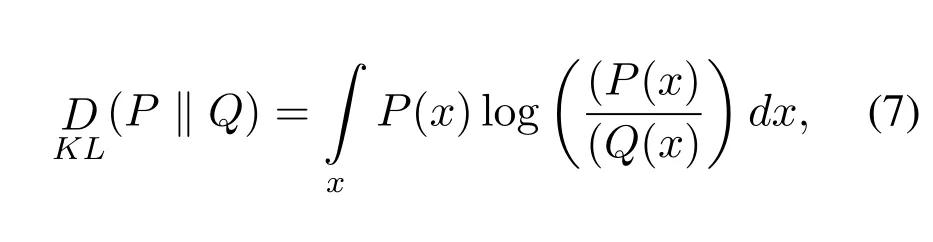
it is important to notice from Equation(7)that KL divergence is asymmetric sinceDKL(P ‖ Q)/=DKL(Q ‖ P).KL divergenceDKLdrops to 0 whenP(x)approaches 0 whenx ＞2.The KL divergenceDKL(P ‖ Q)in Equation(7)penalizes the generatorG,if it misses some data modes of images,the penalty is maximum whenP(x)＞0 butQ(x)→0.The implications of using KL divergence as an objective function forGis,it produces the samples of poorer quality butDKL(P ‖Q)pushes the generator to cover the multiple modes of data manifold,hence it partially solves the problem of mode-collapse in GANs.The symmetric form of KL-divergence is JSD which we have discussed thoroughly in the previous section.

While the forward KL-divergenceDKL(P ‖ Q)pushes the generator to learn more diverse data modes,the reverse KL-divergenceDKL(Q ‖ P)penalizesGfor not generating high quality images while leaving the mode-collapse problem unsolved.Fake images generated using reverse KL-divergence as a loss function show better quality than forward KLdivergence but the reverse KL-divergence based generator is prone to mode-collapse.

D2GAN.Since both the forward KL-divergence and reverse KL-divergence separately solve the problems such as,mode-collapse and image quality,combining both versions of KL-divergence lead to a better adversarial objective function that,not only pushes the generator to cover the multi modes of data but also to generate images of higher quality.Nguyenet al.(D2GAN)[36]proposed a novel approach to address the issues posed by training regular GANs,D2GAN merges both the forward KL-divergence and reverse KL-divergence as a unified loss function to tackle the problem of mode collapse and generated image quality by introducing a three-player minimax game.Unlike the regular GANs[1],that aims to play the minimax game between two playersGandD,D2GAN introduced another discriminator into a two-player minimax game.The objective function of D2GAN for a three-player minimax game is defined as,

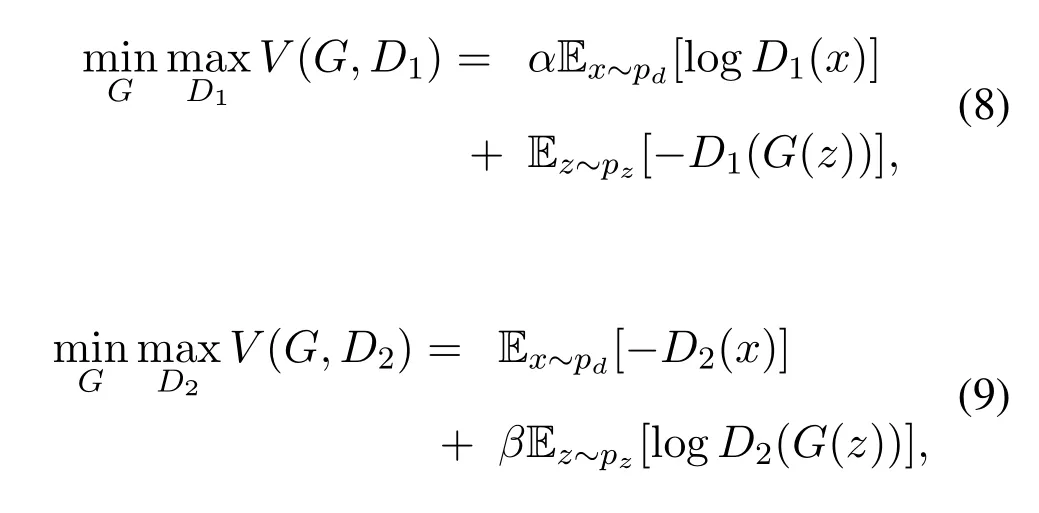
combining Equations(8)and(9)the objective function for D2GAN can be written as,

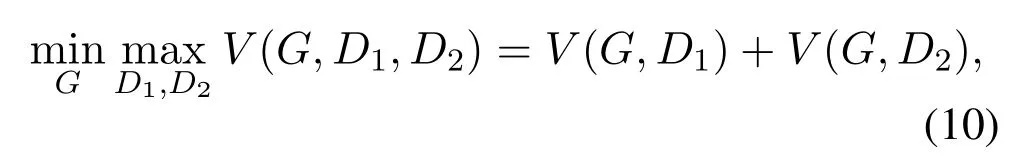
whereD1andD2are the first and the second discriminators,and a single generatorG.D1(x)in Equation(8)assigns a high score if a given samplexis drawn from the real data distributionpd,and assigns a low score if the given sample is from the generated distributionpz.Meanwhile,D2(x)in Equation(9)assigns a high score if the given sample comes from the generated distributionpz,while assigning a low score to the sample from the real data distributionpd.

The scores assigned by the discriminators of D2GAN are the positive real values R+unlike the discriminator of regular GANs that outputs the values as probabilities in the range[0,1].Hyperparameters,αandβrange between 0＜α,β ≤1,normally the hyperparameter configuration values forαandβare varied in{0.01,0.05,0.1,0.2}during the learning process while serving two important purposes.The first goal is toward stabilizing the learning process of the model,since the assigned scores of the respective discriminators are positive and unbounded values,D1(G(z))in Equation(8)andD2(x)in Equation(9)can grow exponentially large during the learning process and have a huge impact on loss optimization thanD1(x)andD2(G(z))in Equations(8)and(9)respectively.To overcome the issue of network instability,D2GAN suggests decreasing the size of the hyperparametersαandβin order to penalize the exponential growth of the probability functionsD1(G(z))andD2(x).The second goal of the hyperparametersαandβis to control the effect of both versions of KLdivergence regarding the optimization problem.

f-GAN.The term f-divergences are a general explanation for all the family of divergences in the probability theory[53]defined in the Equation(2)previously in detail.Based on the idea that the distance between the probability distributions can be calculated in various ways by using f-divergence,Nowozinet al.(f-GAN)[48]proposed that family of f-divergences can be used in GANs as different objective functions.[52]originally proposed a general method for the estimation of f-divergences given the samples from the probability distributionsPandQ,while the estimated divergence is bounded by the fixed model.f-GAN[48]further extended the method originally proposed in[52]from measuring divergence bounded by a fixed model to estimating model parameters.They called this new approach as,variational divergence minimization(VDM)and proved that the generativeadversarial modeling is in-fact a special category of more generalized VDM framework.

According to Hiriaret.al[54]every convex functionfgiven in Equation(2)has a correlated conjugate functionf*also called as Fenchel conjugate of the functionf,defined as,

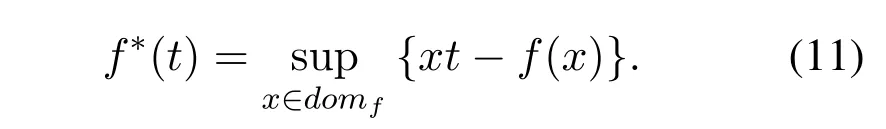
f-GAN proposed a modified version of the above function,considering the fact that the pair(f,f*)is convex and dual so that,f**=f.Thus,the proposed modified version in f-GAN is defined as,

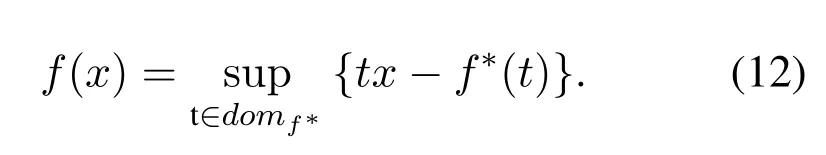
The modified f-GAN function in term of two probability distributionsPandQis formulated as,

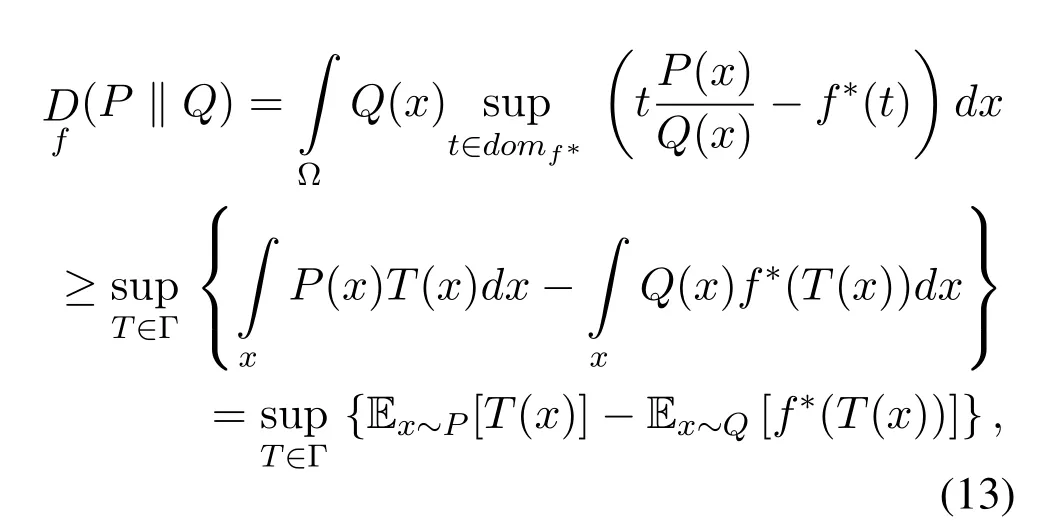
where Γ belongs to a class of arbitrary functions that is,T:Ω→,andis the expectation whileTis a function withxas an input andtas an output.Probability distributionPrepresents the real probability distributionpdof data,and probability distributionQrepresents the generated probability distributionpzof fake samples.f-GAN aims to minimize the divergence betweenpdandpzby minimizing the generator lossf,and by maximizing the lower of bound in Equation(13).Hence,f-divergence is the generalized form of generative adversarial networks.

Among the family of all f-divergence and divergence-based loss functions,we have already discussed some types of f-divergence in the previous paragraphs including JSD,KL,reverse KL,Pearsonχ2,and pros and cons of using different divergences as loss functions for GANs.The most popular and commonly used loss function for GANs based on Pearsonχ2divergence was proposed by LSGANs,which we already have discussed in detail in previous paragraphs.In the next section we discuss the wasserstein loss in GANs and its variants in detail.

4.3 Divergence to Wasserstein Loss

In the previous section we discussed some of the significant divergence-based loss functions in GANs.Wasserstein distance,also known as integral probability metrics(IPMs)[55]is a measurement of distance between two probability distributions over some given metric spaceM.Wasserstein distance can also be expressed as the minimum loss value of turning one probability distributionQinto another probability distributionPon a metric spaceM.

WGAN.In conventional GANs objective function,when the discriminatorDbecomes optimal at discriminating generated distributionpzfrom the real data distributionpd,then the generator of GANs will suffer from serious vanishing gradient problem that is,if two probability distributions have low dimensional data supports,and if they are not a perfect align then the discriminator will be too good at discriminating and the GAN objective function will have zero gradient almost everywhere[33].If the latent noise vectorzthat is used to generate the imageG(z)is of lower dimension than the original imagex,then the discriminatorDlearning accuracy will be maximum at discriminating fake data samples from the real data samples,and the gradient∇D*(x)= 0 almost everywhere,if the expected probability values of generated and real data distributions in JSD,KL and reverse KL-divergence don’t overlap given below,

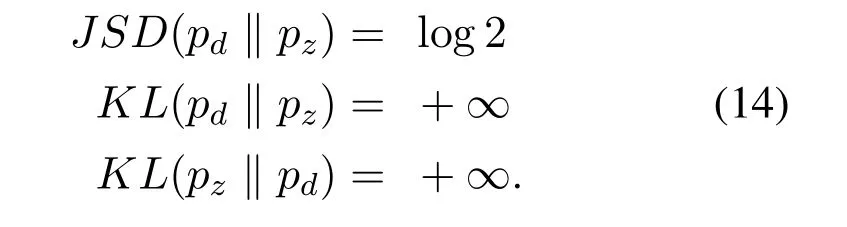
To deal with the problem of vanishing gradients posed by divergences mostly commonly used in regular GANs in Equation(14),Arjovskyet al.(WGAN)[33]proposed Wasserstein loss function to measure the distance between probability distributions,and introduced an alternated solution toward solving vanishing gradient problem.Wasserstein distance between probability distributions is defined as,

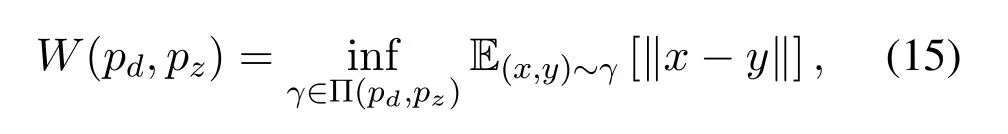
where Π(pd,pz)is the set of all possible joint distributions of probability distributionspdandpz.The joint distribution functionγ(x,y),determines the cost of transferring mass density fromxtoy,so that,the generated probabilitypzbe as close as to the real data distributionpd.Whilexandyrepresent the real and generated data samples,and the difference between them is the expected distance E between the samples of joint distribution.Wasserstein distance is also known as the Earth-Mover distance(EM),the lower bound of the expectation E in all the joint probability distributions can be measured as Wasserstein distance.

The reason why Wasserstein distance is better than both KL-divergence and JSD is,even when two probability distributions are located in lower dimensional manifolds and don’t overlap,unlike KL and JSD,Wasserstein distance still can provide meaningful gradient updates to the generator network that helps the overall GAN network to converge and solves the problem of generator falling into mode-collapse.However enforcing the Wasserstein distance directly in GAN is quite a difficult task.Since it is intractable to dissipate all the possible joint probability distributions Π(pd,pz)to calculateWGAN proposed an alternate method to compute the least upper bound of the Equation(15)based on the Kantorovich-Rubinstein duality,that is defined as,

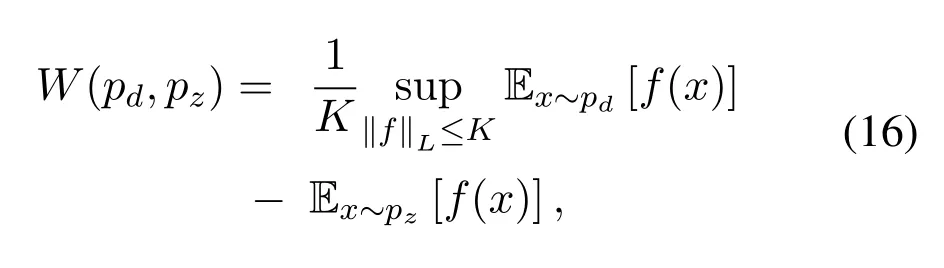
where sup is the opposite of inf,that represents measuring the least upper bound,the functionfis the new Wasserstein metric which is bounded to satisfy the condition of K-Lipschitz continuity,‖f‖L ≤KandKis a Lipschitz constant for the functionf.Any realvalued functionfis K-lipschitz continuous only if there is a constantK ≥0 such that,for allx1,x2∈R,then the K-Lipschitz condition for the Wasserstein distance can be defined as,

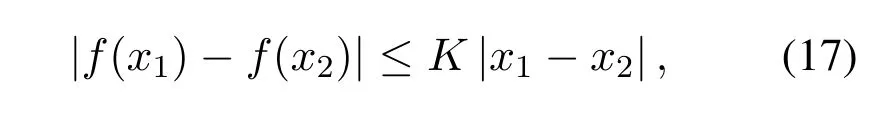
normally the value of Lipschitz constant is set to 1.However it is important to notice that functionsf(.)that are continuously differentiable are Lipschitz continuous but a Lipschitz continuous function may not be differentiable everywhere.If the funtionfbelongs to the family of K-Lipschitz continuous functions,{fw}w∈W,parameterized by the weightswof neural networks,while the discriminator also known as a critic networkCin WGAN is used to learn the weightswto find suitablefw,then the modified WGAN loss in Equation(16)can be simplified to,

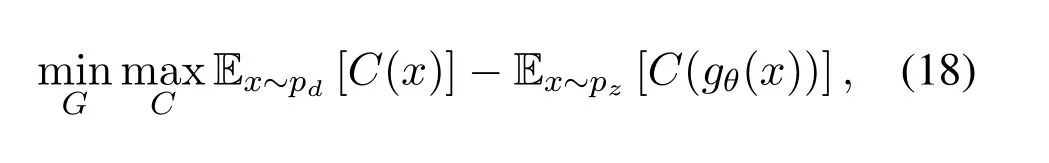
whereCdenotes the critic network in WGAN,unlike regular GANs,where the discriminator is responsible for discriminating fake samples from the real ones directly,the criticCof WGAN instead is trained to learn K-lipschitz continuous function to compute Wasserstein distance.As the loss function decreases during training,the Wasserstein distance becomes minimum,meanwhile the gap between the generated and the real distributions grows smaller.

The problem with WGAN is,during the training the functionfhas to be K-Lipschitz continuous all the time.Since the computation of the Wasserstein distance requires functionfto be strictly K-Lipschitz continuous,the authors of the paper present a simple trick,after every gradient update the weightsware clamped to a small window,such as[-0.01,0.01]so that,functionfmaintains K-Lipchitz continuity.However,Gulrajaniet al.[49]suggested that even weight clamping for the critic network in WGAN does not ensure the convergence of the network,and the quality of the generated samples depletes.

WGAN-GP.In the previous paragraph we discussed about WGAN and how it deals with the problems such as,network instability,mode-collapse and vanishing gradient.However,despite WGAN tremendous success against solving the problems posed by original GANs,the network convergence is still hard to achieve since the weight clipping method proposed in WGAN to improve GANs performance and network convergence,still suffers from unstable training,and convergence is slow after weight clipping when clipping window is too large and if the window size is too small,the generator suffers from vanishing gradients.

To solve such problems in WGAN,Gulrajaniet al.(WGAN-GP)[49]proposed a gradient penalty term to improve network convergence and stability by limiting the gradient of critic network not to exceedK.The orginal Wasserstein loss with added gradient penalty term is defined as,

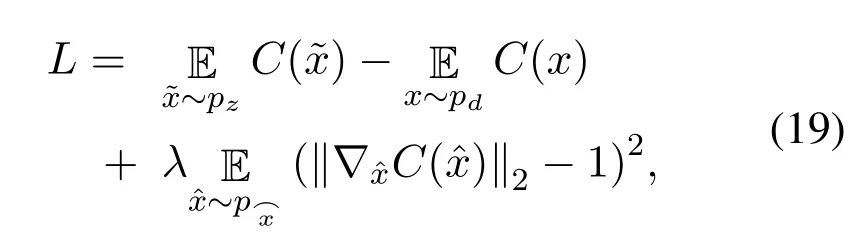
WGAN and its variants have improved the performance of GAN framework by introducing different tricks to stabilize the learning of the network,its convergence,and produced samples of higher quality than original GANs.Another variant of WGAN which does not require the strict K-Lipschitz constraint to be imposed on the loss function of WGAN is called,the Wasserstein divergence for GANs(WGAN-div)[56].WGAN-div proposed a Wasserstein divergence loss based on Wasserstein distance,in their paper they proved that the proposed Wasserstein divergence is symmetric in nature,and the proposed loss function can accurately approximate the Wasserstein divergence(W-div)through optimization.The Wasserstein divergence is defined as,

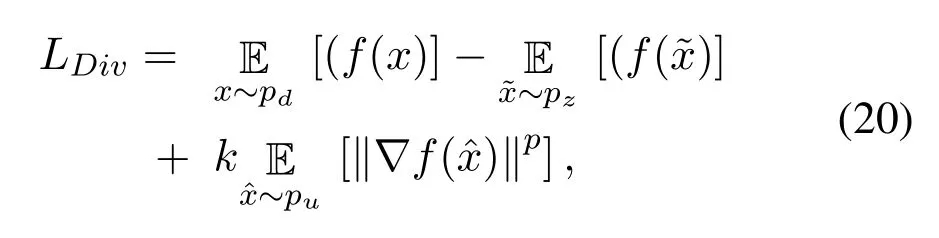
wherepurepresents the measurement of Randon probability,kandpare the hyperparameters to be tuned during the training,usuallyk= 2 andp= 6 are the recommended settings to obtain the optimal FID score,unlike WGAN where the value ofpis fixed to 2.The Wasserstein divergence in Equation(20)can be defined in a GAN framework as,

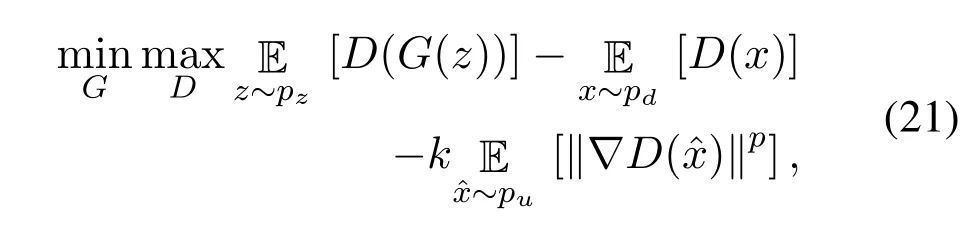
wherezis the random noise sample as an input to the generatorG,andG(z)is the output generated sample,xis the real data sample from the real data distributionpd,D(x)is the probability distribution function of the discriminator network,is the expectation of the Wasserstein divergence between the generated distribution and the data distribution,andkandpare the hyperparameters.The authors of WGAN-div proved that the proposed method achieves minimum values of FID compared to the original WGAN framework.In the next subsection,we discuss some other loss functions besides the family of the Wasserstein loss functions,proposed to slove the problems of mode-collapse,vanishing gradients,and network instability in GANs.

4.4 From Wasserstein Loss to Other Loss Functions

Besides the family of Wasserstein loss,to deal with the problem of unsatisfactory results in GAN modeling,Qiet al.(loss-sensitive GAN)[51]proposed the loss function based on Lipschitz densities.The losssensitive GAN and WGAN are both similar in a way that both of these loss functions are derived from Lipchitz densities but they serve different purposes.In conventional two-player GAN framework,a discriminator and a generator play minimax game,whereas a generator learns to generate realistic looking samples while discriminator learns to discriminate the fake data samples generated by the generator and the real data samples from the real data distribution.

In the conventional GAN framework a generator is supposed to generate the samples of higher quality that can fool the discriminator.However,generating realistic samples from arbitrary data distribution without imposing any prior on data distribution leads to the samples of poor quality and vanishing gradients for the generator network.The loss-sensitive GAN proposed a loss function based on regularization theory to assess the quality of generated samples by imposing a constraint on the data distribution such that,the loss of real samples should be minimum than the loss of generated samples.The loss-sensitive GAN(LSGAN)defines the margins between the losses of generated samples and the real data samples so that,an optimal generator is trained to generate realistic looking samples with minimum losses.The LS-GAN seeks to learn a loss functionLθ(x)parameterized withθby considering that the loss of real sample should be smaller than the generated sample by a preferred margin.The loss-sensitive objective function in a GAN framework is defined in Equations(22)and(23)

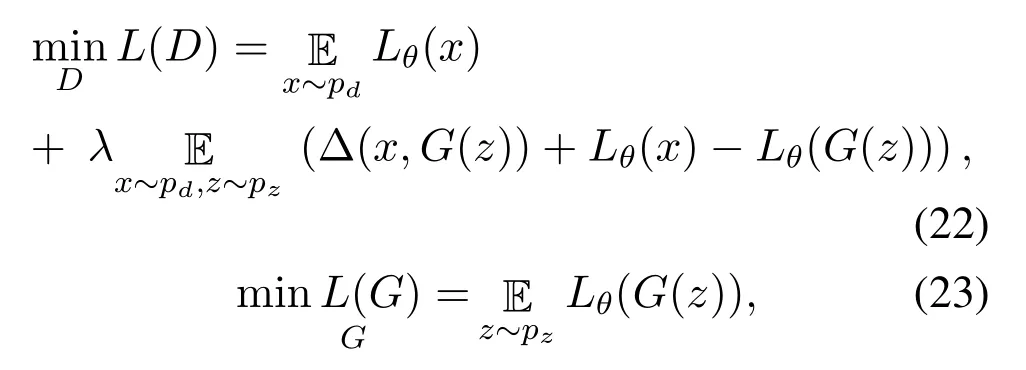
where Δ(x,G(z))is the preferred margin that measures the difference betweenxandG(z)in terms of their respective losses,andλrepresents the positive balancing parameter.It is important to note that the margin in LS-GAN is not a constant term,it is indeed a measurement of similarity based on p-Norm.When the generated data sample is close to the real data sample in a distance metric space,the margin between the generated sample and the real sample vanishes.

Additionally,there are non-probability based methods used in GANs to measure the distributions instead of using Lipschitz density as a constraint on the sample distribution.Zhaoet al.(EBGAN)[34]assumes the discriminator as an energy measurement function that classifies the data regions into lower and higher energy regions.The energy regions near the real data manifold are classified as low energy regions and higher energy regions are considered further away from the real data manifold.Similar to regular GANs,the generator of EBGAN is trained to generate samples that belong to the low energy regions of data manifold,while the discriminator as an energy measurement function is trained to assign high energy values to the samples generated by the generator.Unlike the discriminator of regular GANs,the discriminator of EBGAN is an auto-encoder with the measurement of energy as the reconstruction errorD(x)=‖Decoder(Encoder(x))-x‖.EBGAN argues that in place of logistic discriminator of regular GANs,the proposed energy measurement function shows more stable behaviour during training than the discriminator of regular GANs.The objective function of EBGAN is defined in Equations(24)and(25),

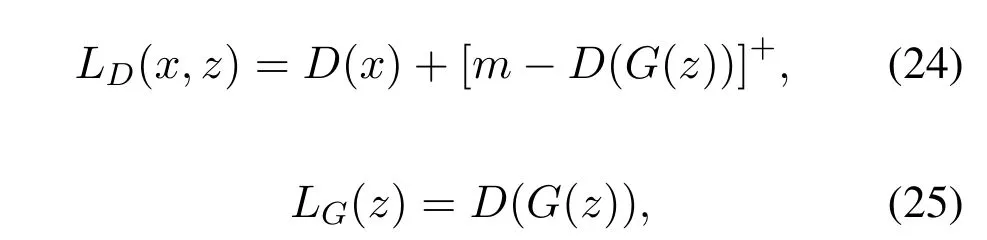
where[·]+= max(0,·),andmindicates a predefined positive margin that controls the ability of the energy function to allow the generator to converge continually.In order to enable the generator to generate diverse samples,the EBGAN proposed a repelling regularizer method in the generator loss that pushes the generator to learn the different modalities of the data.However,implementation of repelling regularizer method requires a Pulling-away term(PT)which is defined in Equation(26),

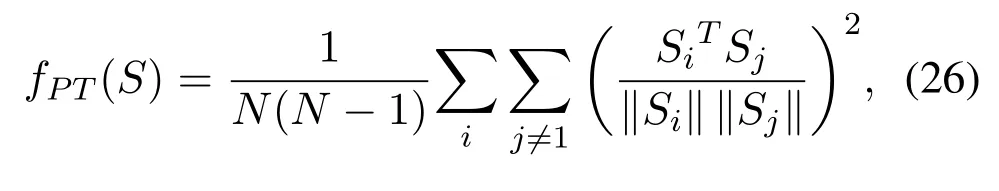
where the coding layer of the discriminator is represented byS.When the value of PT increases the diversity of generated samples increases.

Energy-based estimation in GAN framework has proven to be more stable during training,and enabled the generator to generate more diverse samples by learning multi-modes of the data manifold.Boundary equilibrium GAN(BEGAN)[50]is another example of the energy-based estimation in GAN modeling that combines the loss effective properties of the WGAN and EBGAN to assess the generative ability of generator.Berthelotet al.[50]proposed an equilibrium enforcing method that balances the generator and discriminator during training by employing a simple auto-encoder based network architecture.In addition to equilibrium enforcing method,the proposed BEGAN seeks a way of limiting the trade-off between the image diversity and the image quality of the generated samples.

Unlike regular GANs that tries to measure the difference of probability distributions directly,the BEGAN on the other hand seeks to measure the difference of auto-encoder loss in probability distributions using a loss function based on the Wasserstein distance.The BEGAN analyzes the effects of comparing the distribution of errors between the generated and the real data samples,by computing the lower bound to the Wasserstein distance.The objective function of BEGAN is defined as,

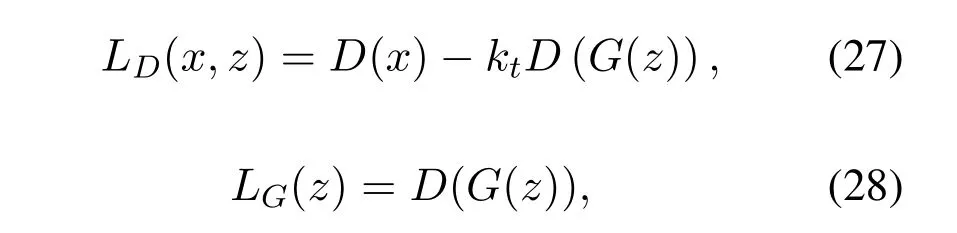
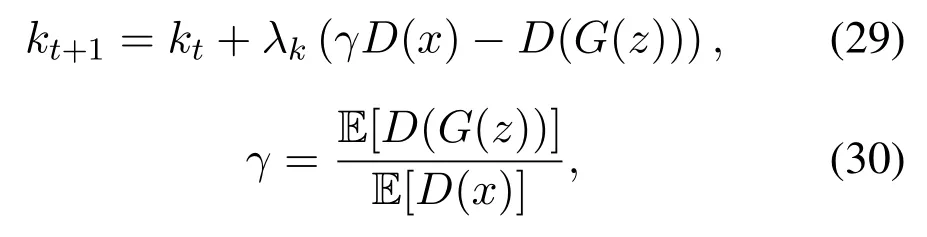
whereγis the diversity parameterγ ∈[0,1](image diversity depends on the value of the parameterγ,the lower value ofγrepresents the lower diversity in the generated images).kis the variable from Proportional Control Theory to maintain the equilibrium between the generator and the discriminator,initially it is set to 0 in the early stages of the training,so that the autoencoder function can be learnt properly.The learning rateλkfor the variablekis set to 0.001 during the training.

To summarize Section(IV),we have discussed about the recent adversarial-based loss functions,and the adversarial game between the generator and the discriminator in GAN framework.The generator in GAN implicitly maps a probability distribution,and on the basis of this generated probability distribution,the generator generates fake data samples.The discriminator on the other hand,measures the difference between the generated samples and the real data samples,and the calculated loss is back-propagated to the generator.Therefore,the goal behind this adversarial game is to enable the generator to generate samples as close as to the real data distribution of datasets while maintaining the equilibrium between the two competing networks.The divergence-based loss functions we discussed earlier in this section,heavily rely on the real data distribution.However,the disadvantage of using divergence-based loss functions(also known as f-divergences)is,when the support of the generated probability distribution and the real data distribution is a low dimensional manifold that lies in a high dimensional space,the two probability distributions do not overlap,or the overlap is minimum[25].At this stage of training,the problem of vanishing gradient occurs,and the generator is unable to learn the data manifold,which further increases the training difficulty.To deal with the problems posed by divergencebased loss functions,the Wasserstein loss function and other integral probability metrics(IPMs)stabilize the training of the network,and show better ability of network convergence because of the continuous nature of the IPMs almost everywhere,even when the two distributions have no supports.

Additionally,other proposed loss functions such as,the EBGAN and BEGAN are both energy-estimation networks.The discriminator in both of these methods is an energy function defined as an auto-encoder.The EBGAN fails to address the problem of model convergence and its dependency on data distribution.BEGAN on the other hand,used Wasserstein distance to match the distribution of errors instead directly matching the generated distribution and real data distribution,therefore,BEGAN is shows better training stability,and effectively addresses the problem of modecollapse.We also discussed the pros and cons of these loss functions in detail.All these loss functions in GANs either try to solve mode-collapse or vanishing gradient problem,and propose non-trivial solution space for the problems faced by GANs.However,the proposed loss functions cannot completely suppress either mode-collapse or vanishing gradient,which still poses many challenges to the training of GANs and network stabilization,yet it opens up new opportunities for the research in GANs that can provide solutions to the problems faced by GANs.In the next section,we discuss the architectural evolution in GANs and the impact of loss functions.

V.ARCHITECTURAL EVOLUTION IN GAN AND THE IMPACT OF LOSS FUNCTIONS

In this section,we study the methods that scale up the GAN model from two-player to more than two-player game,and the impact of loss functions in these models.In recent years,almost all the GAN architectures are deep convolutional in nature,Radfordet al.(DCGAN)[32]proposed a deep convolutional architecture for both the generator and the discriminator of GAN,the architecture of a deep convolutional generator in given in Figure 2.

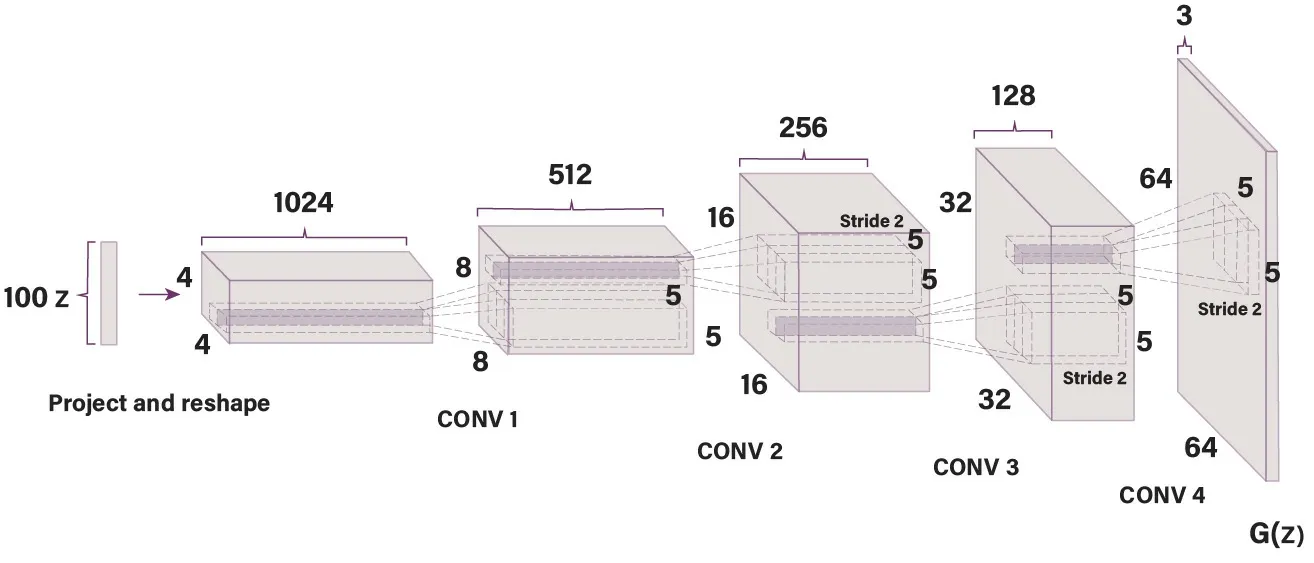
Figure 2.The architecture of a deep convolutional generative network.A random noise vector z of dimension 100 as input to first layer of the generator model.A sequence of four stirded convolutional layers and the final output is a 64×64 generated image.

5.1 Multi-generator Discriminator Networks

MAD-GAN.Integrating the multi-agent algorithm[57]with the coupled-GAN[58],Goshet al.(MADGAN)[38]proposed a GAN model with multiple generators,and a single discriminator network.The goal of each generator is to generate realistic looking samples so that,the common discriminator can be fooled.MAD-GAN multiple generator model acts as a mixture model with individual generators focusing on one mode each.However MAD-GAN argues that using multiple generators in a GAN framework can cause trivial solution,where all the multiple generators focus on learning on only a single mode of data while generating similar samples.To solve this issue,and to make generators capable of generating plausible generated samples,the authors of the paper propose to modify the objective function of the discriminator.The modified discriminator function not only discriminates the fake samples from the real data samples but also correctly recognizes the generator to which a generated sample belongs.

Besides modifying the objective function of the discriminator,MAD-GAN also introduces a diversity enforcing method that maximizes the diversity among the samples generated by multiple generators.The proposed modified discriminator enables the multiple generators to learn the real data distribution as a mixture of distributions.when the overall model converges,the global optimum-(k+ 1)log(k+ 1)+klogkis achieved,wherekrepresents the total number of generators.The objective function of MADGAN is defined as,

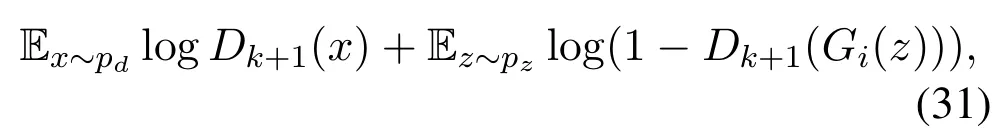
whereDk+1represents the probability that the sample is from the real data distribution,unlike the discriminator of regular GANs that outputs a binary value,the modified discriminator of MAD-GAN outputsk+1 soft-max scores,andGiis thei-th generator.To further explain the diversity enforcing method in a group ofkmultiple generators for which the discriminator provides soft-max probability distribution givenk+1 set of classes,and the score atj-th index wherej ∈{1,....,k}indicates the probability of a generated sample that belongs to thej-th generator.While training the discriminator,the goal is to optimize the crossentropy between the soft-max scores of the discriminator and the Dirac delta distributionδ ∈{0,1}k+1,whereδ(j)= 1 if the generated sample is generated by thej-th generator,otherwiseδ(k+1)=1.The loss function for the discriminator function while holding the generator fixed is defined as,

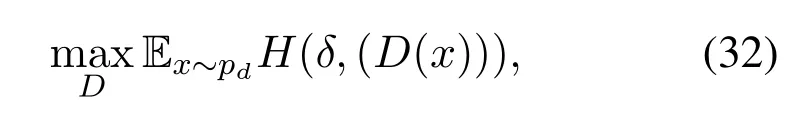
whereHrepresents the optimization of cross-entropy between the Dirac delta distributionδand the soft-max scores of the discriminator.The collective loss function to be minimized for the all the multiple generator is defined in Equation(33).

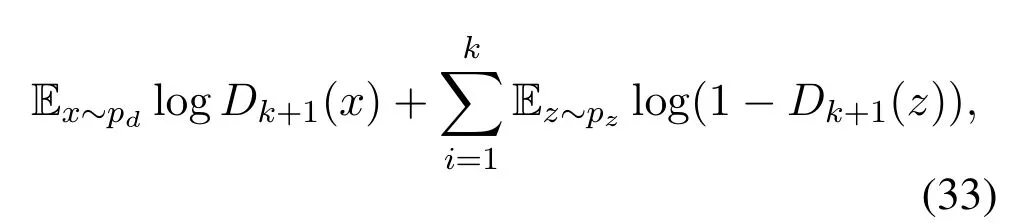
the collective loss function of generators in Equation(33)is equivalent to minimizing the KL-divergence between the mixture of generated distributions and the real data distribution.

MGAN.Training GANs with multiple generators,Hoanget al.(MGAN)[39]proposed a method of training multiple generators simultaneously,in a spirit that the mixture of their combined distributions would approach the real data distribution.The adversarial game in MGAN is played among three players:a set of multiple generators,a discriminator function,and a multi-class classifier.The set of multiple generators learn to generate plausible samples by focusing on the problem of mode-collapse.The discriminator function similar to regular GANs distinguishes fake sample from the real data sample,and the classifier classifies the generated sample according to the generator that generated the sample.To further explain the minimax game among three players,the JSD is used as a measurement of difference between the mixture of combined generated distributions and the real data distribution.

To deal with the problem of mode-collapse the JSD among the set of multiple generators is maximum,while the JSD between the mixture of combined generated distributions and the real data distribution is optimized to its minimum.The proposed MGAN model shares the parameters among multiple generators,and between the discriminator and the multi-class classifier.Sharing the parameters among generators improves model’s learning efficiency,and maximizing JSD among the generated distributions of generators solves the problem of mode-collapse,so that,different generators learn different modes of the data.The objective function for MGAN is defined as,

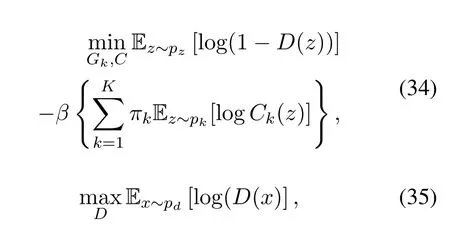
whereCk(z)represents the probability that the generated samplezis generated byk-th generator,βis diversity parameter that varies inβ={0.25,0.5,0.75,1.0},andπ=[π1,π2,...,πK]represents coefficients of the combined distributions drawn from a multinomial distribution,the coefficientπis a constant parameter which is fixed to{1,....,K}.Unlike(MADGAN)[38]that trains multiple generators and utilizes the discriminator as a classifier,the MGAN model proposed two methods to deal with the problem of mode-collapse:(1)encouraging multiple generators to produce diverse samples by maximizing the JSD among them,and(2)pushing generators towards different data modes by using an additional multi-class classifier network that distinguishes samples generated by each generator.

5.2 Evolutionary Computation for GANs

E-GAN.Evolutionary generative adversarial networks,Wanget al.(E-GAN)[47]proposed evolutionary computation mechanism for training GANs.Evolutionary algorithms have been used in a variety of tasks and they have attained substantial success in modeling,design and optimization[59—62].In comparison with regular GANs,where a generator and discriminator take turns to be updated,E-GAN proposed a network with population of evolving generators and a shared environment among evolving generators(i.e the discriminator network).This idea is based on evolutionary algorithm,where a population of generators provide a set of possible solutions to a problem,each individual generator is evolved to provide a better solution in the space of generative parameters.During the process of evolving generators from a given set of generative networks,it is expected that the population of evolved generators approximates the environment,which further indicates that the evolved generators learn to generate realistic samples by learning the real data distribution.

The evolutionary process in generative network is carried out in three stages:(a)Variation,(b)Evaluation,and(c)Selection.

·Variation:Variation is the process in which offspring of a given generatorGθare created,and each offspring in{Gθ1,Gθ2,...,Gθk}is modified through different mutations.Each mutated offspring represents a single child.Three different types of loss mutations are provided,starting from the minimax mutation,heuristic mutation,and the least-square mutation.The minimax mutation represents the minimax objective function in the regular GANs,defined as,

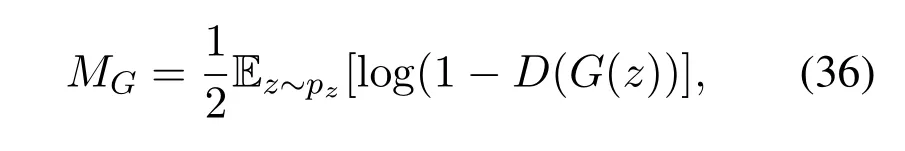
the goal of minimax mutationMGlike GANs is to minimize the JSD between the generated distribution and the real data distribution by providing effective gradients to the evolving generators.Heuristic mutation on the other hand maximizes the log probability of the discriminator being fooled by the generated sample.it is defined as,

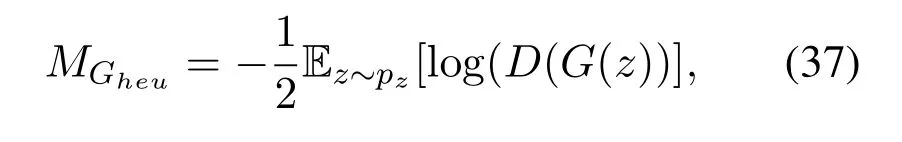
the heuristic mutationMGheudeals with the problem of vanishing gradient by providing useful gradient updates to the generator.Finally,the least-square mutation doesn’t saturate when the discriminator can correctly classify the generated sample from the real data sample,and can avoid mode-collapse problem.Least-square mutation is defined as,

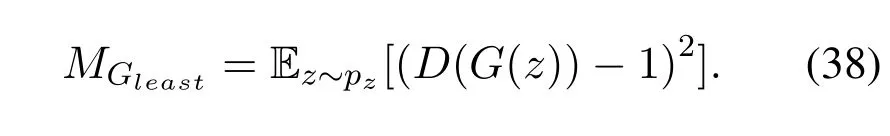
·Evaluation:E-GAN proposed a method of measuring the quality and the diversity of generated samples through a fitness function.The quality of generated samples depends on the learning process of the generators,and how well a generator is able to fool the discriminator with generated sample.The diversity of generated samples refers to the different modes of the data manifold which is,whether a generator network has learnt all the modes of the data or it has only learnt few modes of the data.For the measuring the quality of generated samples the fitness function is defined as,

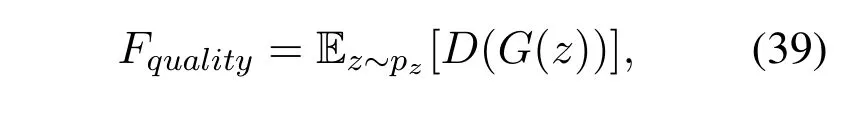
where the fitness quality functionFqualityis the expected average value of all the generated samples.The diversity fitness function which encourages each individual generator of the population to generate diverse samples is defined as,

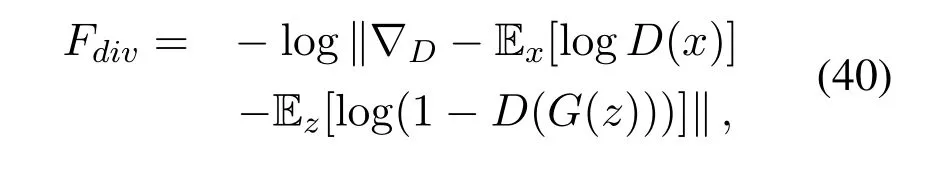
where-log in Equation(40)represents the gradient-norm for optimizing the discriminator network and measures the diversity of generated images.Combining the two fitness functions in Equations(39)and(40),the final evaluation function can be described as,

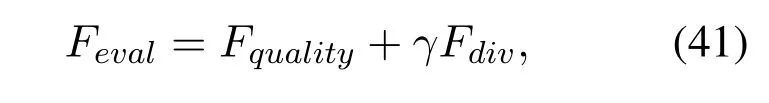
whereγ ≥0 is a balancing parameter between the generated image quality and the generated image diversity.The higher values of evaluation functionFevaltends to improve the training efficiency and generating ability of generators.

·Selection:Based on the factors such as,quality of the generated images and the diversity of generated images,a selection strategy is devised to select the next generation of evolved generators based on the fitness function of each individual generator.The best individual generators are selected to produce new offspring by sorting out the fitness score values of each individual generator and then,selecting the best set of generators.

However,it is important to notice that adding multiple generators through the evolutionary process adds further complexity to the network with the exponential increase in the training time of the overall network.Optimizing different loss functions as different mutations to the generators solves the problem of modecollapse up to some extent but on the cost of training efficiency.

5.3 Other GAN Architectures

Stacked-GAN.Stacked generative adversarial networks,Huanget al.(SGAN)[63]proposed a model to train a top-down stack of GANs against a bottomup discriminator network,each stack of GAN learns to produce lower-level data representations based on higher level data representations.Unlike the regular GANs,each generatorGiin the stack of GANs is conditionally connected with an encoder and receives a conditional input in a separate training process,and the input from the predecessor generators in the stack of generators in a combined training process.The goal of the top-down hierarchy of generators is to learn to produce plausible features for which the respective representation discriminatorDican be fooled.Meanwhile,Table 5.presents the reported inception and FID scores of different GAN approaches on two largescale datasets,CIFAR-10 and LSUN.It is important to notice that,higher values of inception score(IS)rep-resent better performance while lower values for FID are better.

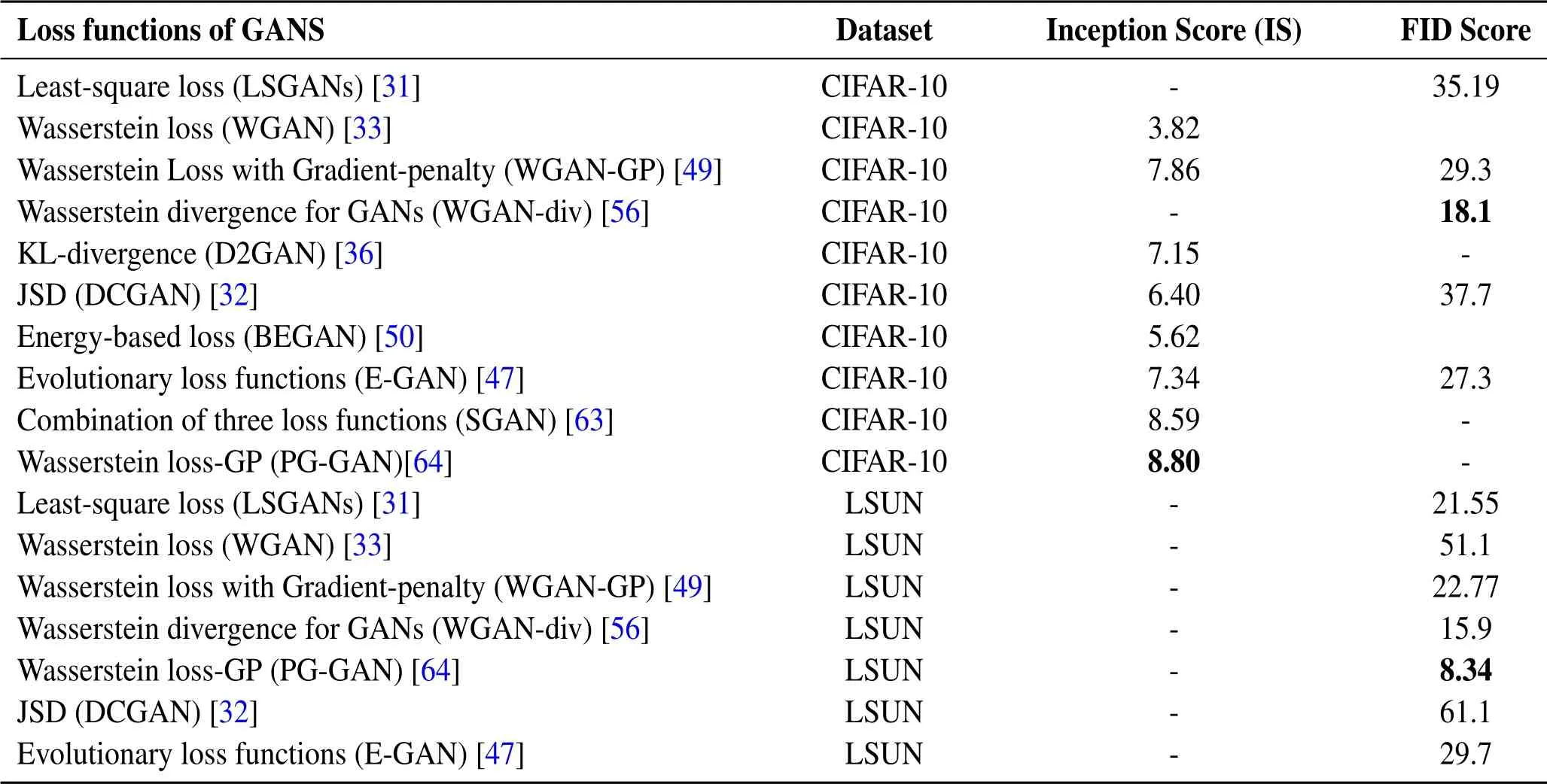
Table 5.Comparison of different loss functions based on Inception and FID scores.

The generators of the SGAN are trained to transpose the input representations of a bottom-up encoderEi.Each individual generator operates on two data inputs,the higher level feature and the random noise vector,and produces the low feature ˆhi.

SGAN model is trained in an encoder-decoder fashion,where an encoder is a pretrained model that takes an imagexand predicts its associated labely,and a decoder takes in labelyand the random noise vectorz.The learning of the encoding-decoding in SGAN is performed in a sense of a stack.To understand a single level encoder-decoder method,firstly a real data imagexis fed into the encoderE1to predict the labely,then the labelyalong with the noise vectorzare fed into the generatorG1to generate a fake image ˆx.The generated image is forwarded back to encoderE1to predict the label again.Since there are two predicted labels one for the real data image and the other for the generated image,hence the loss function to train the generator consists of three different loss functions defined as,

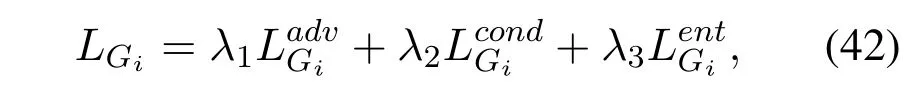
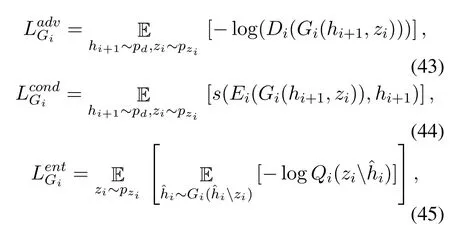
There are several other approaches that improve the generative performance of GAN in terms of,image quality,image diversity,and model convergence either by adding more generators and discriminators in the network architecture or by proposing the new optimization methods,and loss functions in a two-player GAN framework[65—67].One such example of growing a generative network by proposing a new training method for GAN,that progressively increases the resolution of generated images by adding new layers during the training process is called progressive growing of GANs for improved quality,stability and variation(PG-GAN)[64].Generating high-resolution fake images from low-resolution images as an input to the generator is somehow a difficult task,the reason behind generating high-resolution from a low-resolution input is,high-resolution images can be easily be classified as fake or real[68],thus effectively dealing with the vanishing gradient problem.However,generation of high-resolution images requires smaller minibatches for the training data due to the limited memory issues,while PG-GAN grows generator and discriminator progressively from low-resolution images to high-resolution images by adding new layers of high-resolution details,meanwhile as the training process progresses all the preexisting layers in both the generator and discriminator remain trainable.The progressive growing GAN(PG-GAN)utilizes the loss functions of WGAN-GP and LSGAN.

To summarize Section V,we reviewed some of the notable GAN architectures,loss functions,and the evolution from a conventional two-player GAN to multiplayer generators and discriminators networks.Addition of extra players into the adversarial game between the generator and the discriminator specially,tackles the problem of mode collapse when there are more than one generator in a generative network,which indicates that multiple generators will be able to learn the diversity and the variation of the training data by covering different data modes.Adding multiple discriminators on the other hand tries to solve the problem of vanishing gradient by providing sufficient gradient updates to the generator so that,the network can show convergence.Meanwhile generative networks such as,PG-GAN add new high-resolution layers on top of low-resolution layers in both the networks to generate high-resolution images from low-resolution inputs,and shows faster network convergence,better training stability,and high quality results than other GAN approaches.However adding more players into the generative framework increase the training time,and adds further complexity,specially when the generated images belong the class of high-resolution images.

In this section,we also discussed architectural evolution in GANs by providing different variants of GAN frameworks and their loss functions.Multigenerator discriminator networks as we discussed in this section thoroughly,provide solutions for tackling mode-collapse problem by defining more than two players in an adversarial game,so that,each additional player focuses on covering different modes of data and generating a blended mixture of all the generated distributions that can approximate the real or true data distribution.However,adding additional deep networks can increase the overall training time for the network,also adding more players to the network does not guarantee the optimal performance of the network when the training dataset contains large inter-class variations or redundant data in the intraclass.In contrast with simply adding multiple players into the network,evolutionary computation proposes selection of the fittest criterion for the optimization of GAN framework.However,similar multi-generator discriminator networks training GANs based on evolutionary selection scheme increases training time exponentially and presents its own challenges.In the next section,we provide experimental results on different GAN framworks.

VI.RESULTS

In this section,we show the results of some generative adversarial networks and the performance of different adversarial loss functions.Furthermore,we show the quantitative evaluation of the adversarial loss functions,and the visual comparison of these results is presented based on the pros and cons of the loss functions used in different GAN frameworks.

6.1 Evaluation Metrics

The evaluation of generative models is still an active research area,different evaluation metrics have been proposed to precisely evaluate the performance of different GAN frameworks,but two evaluation metrics(Inception Score(IS)[28]and Fr´echet Inception distance(FID)[69]have been used more often to evaluate the generating ability of GANs.Generative adversarial networks have shown remarkable performance in generating both high-quality and large synthetic images in range of different problem domains.However,GANs lack an objective function,that measures the generating ability of a generator network,and to compare the performance of different GANs[28].While several metrics have been proposed to best capture the strengths and the limitations of GANs,yet there is no single best metric measurement that highlights the performance of an overall GANs,and provides a fair model comparison[70].

Inception Score(IS).The inception score was first proposed by Salimanset al.[28].To calculate the inception score of a generative network,a pre-trained deep learning neural network has been used to classify the generated images based on the similarity between a generated image and the real image data class,more specifically,the Inception v3 model is used as a pretrained classifier[71].The generated images are classified by calculating the probability of generated images belonging to each class.The predicted probabilities are then converted into the scores to measure the degree of similarity between a generated image and a known class it belong to,and the diversity of generated images across the known class.A higher inception score refers to better quality in generated images,inception score is defined as,

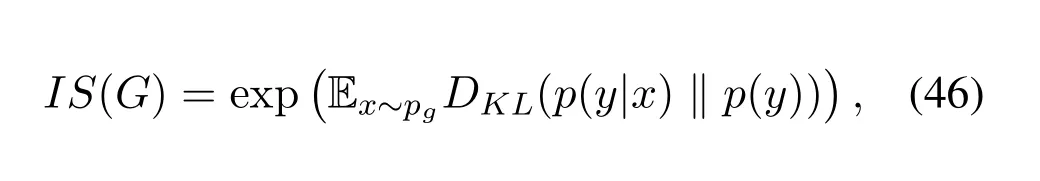
wherex ～pgrepresents a generated imagexfrom a generated probability distributionpg,DKLrepresents the KL-divergence between the probability distributionspandq,p(y|x)represents the conditional class distribution,andp(y)is the marginal distribution.However,Barrattet al.[72]described several issues related to the inception score such as,suboptimalities of IS,sensitivity to weights,and score exponentiation.

Fr´echet Inception distance(FID).To solve the issues posed by the inception score(IS),Heuselet al.[69]proposed a distance metric also known as the Wasserstein-2 distance[73],to calculate the similarity between a generated sample and a real data sample.Like the inception score,FID utilizes the inception v3 model to classify the data.Specifically,the last pooling layer in the inception v3 model is used to capture vision related features of an input image.These activation functions are then calculated for a set of generated and real data samples.The activation functions for each generated and real sample are defined as multivariate Gaussian distribution,and the distance between these two distributions is calculated as FID score.The lower score obtained from FID represents more realistic images that align well with the properties of real image dataset.The FID score is defined as,

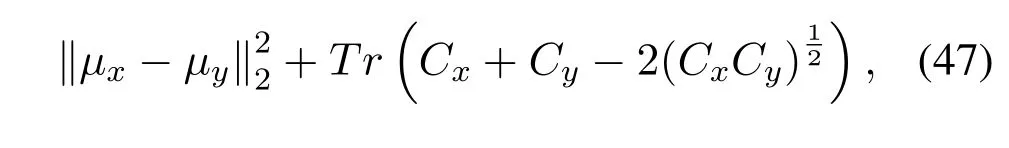
where(μ,C)represent the feature-wise mean and the covariance of the real data samplexand the generated data sampley,andTris the sum of all the diagonal values.

6.2 Image Datasets

MNIST Dataset.The MNIST dataset[74]is the most widely used dataset for image generation tasks.The MNIST dataset consists of 70,000 grayscale images of digits,from 0 to 9,of which 60,000 images are the training images and 10,000 images are the test images.Each image is of size 28×28 in height and width,and 784 pixels in total.

CIFAR-10 Dataset.The CIFAR-10 dataset[75]consists of 60,000 images of real objects,divided into 10 different mutually exclusive classes with 6000 images each class.The images are of dimension 32×32 in height and width,and 50,000 images as the training dataset while 10,000 images are reserved for testing.

CelebA Dataset.The celebA dataset[76]consists of more than 200K diverse images of celebrity faces with 10,177 number of identities,202,599 images celebrity faces,5 landmark locations,and 40 binary annotation attributes per image.The celebA dataset plays an important for training and testing the performance of generative adversarial networks,specially generating facial attributes such as,eyes,nose,lips and other facial features.

LSUN-bedroom Dataset.The LSUN-bedroom dataset[77]contains more than 303K diverse images of bedrooms,however the original LSUN dataset contains around a million images divided into 10 scenes and 20 different object categories.All the images are resized so that,the smaller dimension is set to 256.

STL-10 Dataset.The STL-10 dataset[78]is basically used for unsupervised feature learning of images.The STL-10 dataset is similar to CIFAR-10 dataset but with some additional modifications,specially,each class in STL-10 contains fewer labeled data than CIFAR-10,but a quite large unlabeled dataset of 100,000 images is provided for unsupervised learning tasks.The images in the STL-10 dataset are divided into 10 different classes with the image dimension of 96×96,500 training,and 800 test images per class.The STL-10 dataset is most commonly used as a substitute for ImageNet dataset,because of the enormous size of the ImageNet dataset it is difficult to train a large dataset considering the limited computational resources.

6.3 Generated Results of Two-player GANs

In this section we show the experimental results of two-player GANs,in which both the generator and the discriminator networks play an adversarial minimax game against each other.Our experimental results are carried out on different image datasets such as,MNIST,CIFAR-10,and CelebA datasets.We also report the generated results of existing GAN frameworks on these datasets.For MNIST dataset the results are shown in Figure 3,we have trained the different GAN frameworks on 25 to 50 training epochs by keeping the network architecture of WGAN[33]and the deep convolutional generator of DCGAN[32]as described in Figure 2.In Figure 4 we show the quantitative comparison of different GAN frameworks on MNIST dataset based on the inception score(IS)and Fr´echet Inception distance(FID).The higher values for the IS show the better performance of GANs while for the FID,the lower the values the better is the performance of GANs.Least-square GAN[31]in our experiments achieves the highest Inception score of 5.58 and the lowest FID score of 4.34,WGAN-GP[49]achieves IS of 5.30 and FID of 10.57 quantitatively in Figure 4.

Figure 3.MNIST generated results from different GAN loss functions on training epoch 01,epoch 25 and epoch 50 for each generative model.

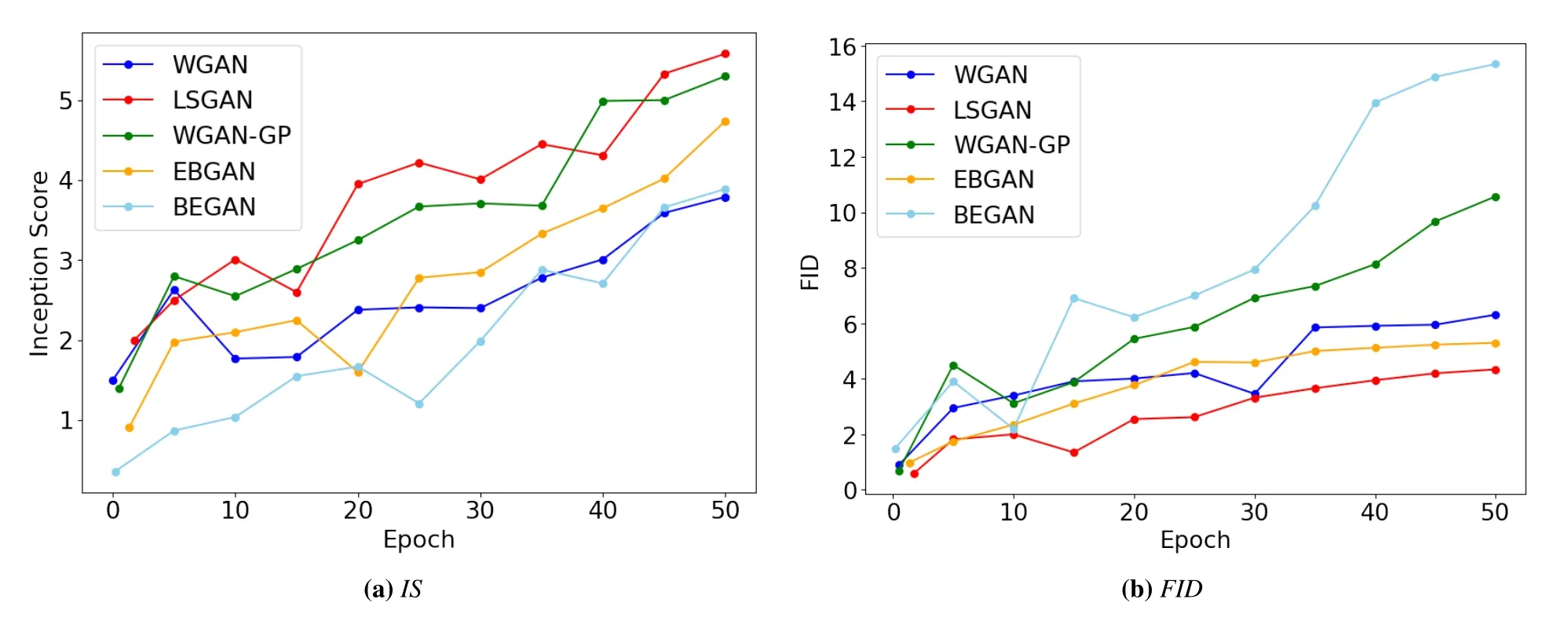
Figure 4.Inception and FID scores on MNIST dataset,higher score values of inception score(IS)indicate better performance while lower values of FID show better performance.

Figure 5.CIFAR-10 generated images of size 32×32 from different GAN loss functions.

However GANs are sensitive to the changes such as,network architecture,tuning of the hyper parameters,and selection of loss functions.Since GANs lack an objective function,and the generator network relies on the gradient updates from the discriminator network,it can cause vanishing gradient in some cases when a weak discriminator is unable to provide enough gradient updates back to the generator,which further decreases the quality of generated images.While on the other hand,when the generator is unable to learn all the data modes and produces data samples for few data modes,it causes the problem of mode-collapse.Therefore,a careful selection of a GAN model is required along with the tuning of its hyper-parameters.We have thoroughly discussed the problem of vanishing gradient and mode-collapse in previous sections,but to further elaborate on the solutions to avoid these problems in a two-player GAN framework,we summarize some techniques to improve the performance of GAN.In an adversarial game a generator tries to generate realistic samples to fool the discriminator,but the generated images keep changing during the adversarial process.However,the optimization process can become too greedy and fall into a never-ending game in which,none of the adversaries wins.This is one of the worst case scenarios where a GAN model doesn’t converge and collapses.To reduce the possibility of non-convergence and mode-collapse in GAN models,feature matching was proposed[28]that changes the loss function of the generator to minimizing the difference between the features of real images and the generated images.Therefore,feature matching plays an important role in the adversarial game between the generator and the discriminator for matching the features of real and the generated images.However,feature matching alone doesn’t guarantee either the network convergence or solving the problem of modecollapse.Many image datasets come with class labels,one such example of conditional labeling in GAN is proposed by Mirzaet al.[46],in which,additional class labels are provided along with the latent vectorzto stabilize the training process of GAN.

Another method that uses the gradient penalty to avoid the local equilibria presented by the discriminator is proposed by Kodaliet al.[79],and the training process of GAN is hypothesized as regret minimization between two players,the generator and the discriminator.To evaluate the qualitative and quantitative performance of different GAN loss functions,we performed the experiments on MNIST dataset in Figure 3 and on CIFAR-10 dataset in Figure 5 and the quantitative comparison on CIFAR-10 in Figure 6.Least-sqaure GANs(LSGAN)[31]in Figure 4 outperforms all the other GAN approaches by achieving the highest inception score,and the lowest FID score on MNIST digit dataset.While BEGAN[50]struggles to generate realistic samples,and exhibits modecollapse on few data modes along with the highest FID score of 15.34 on MNIST.The qualitative and quantitative comparison of different GAN methods on CIFAR-10 dataset is shown in Figures 5 and 6,however,during the training process we observe that LSGAN shows better training stability than other GAN methods,and achieves the lowest FID score of 9.90 on CIFAR-10,and WGAN-GP achieves the highest Inception score of 6.22 on CIFAR-10.The generated samples from BEGAN Inception score of 4.45 and FID of 15.7 are blurry and of unrecognizable objects.WGAN achieves IS of 5.0 and FID of 11.21 and EBGAN IS of 5.30 and FID 12.10,and WGAN-GP on the other hand,performs well in terms of stabilizing the learning of the network,but are slower to converge.

In Figure 7 the generated results on CelebA dataset are shown by training the model for maximum 50Ktraining iterations,and each epoch consists of about 1.58Ktraining iterations for the batch size of 128.WGAN in Figure 7(a)is trained using DCGAN architecture for 50Ktraining iterations,However the generated results from WGAN on CelebA dataset show low visual quality.WGAN-GP in Figures 7(b)and 7(c)is trained using ResNet architecture[80].However,when WGAN-GP is trained using DCGAN architecture,we observe that the quality of generated samples doesn’t improve and produces unrecognizable faces,while WGAN-GP when trained using ResNet architecture generates the best quality images in the very early stage of training for 7Ktraining iterations shown in Figure 7(b),but as the training progresses the quality of the generated images keeps degrading for 50Ktraining iterations as shown in Figure 7(c).For LSGAN in Fig.7(d)we use the DCGAN architecture for 50Ktraining iterations,and with the latent vectorzof dimension 100 generates good quality images.Unlike in Figure 7(e)when the dimension of latent vectorzis increased from 100 to 1024,the quality of generated images drops,while LSGAN in Figure 9 achieves the highest Inception score of 8.90 and the lowest FID score of 9.98 on CelebA dataset in comparsion with other GANs in our experiments,WGAN-GP[49]achieves IS of 8.40 and FID of 10.90 and rest of the GAN methods perform poorly.EBGAN in Figure 7(f)is trained using DCGAN architecture with Pulling-away Term(PT)as described in the original paper[34].The PT in our experiments prevents the generator of EBGAN from collapsing,and generates images of slightly better quality than the EBGAN model without the pulling-away term(PT).The best visual quality results on CelebA in our experiments are achieved by BEGAN in Figure 7(g).However,the generated results of BEGAN are slightly blurry,this is because of the auto-encoder structure in BEGAN model.Therefore,when selecting and training the different GAN models,it is important to choose the stable network architecture and tuning of the hyperparameters.GANs are sensitive to changes and may produce best or worst generated results depending on the optimization of the GAN model,the loss functions,and the architecture of the network.In Figure 8,the reported results of BEGAN[50]with the generated image dimension of 128×128 for 200K training iterations are shown.It is notable from the Figure 8 that,when the dimension of generated images increases,the generator of BEGAN generates high quality samples.However,BEGAN tends to generate the faces of females more often than the male faces.

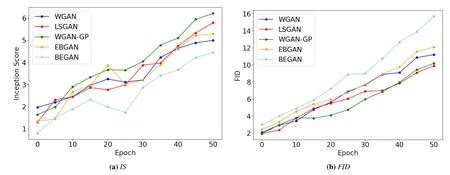
Figure 6.Inception and FID scores on CIFAR-10,WGAN-GP achieves the highest Inception score and LSGAN achieves the lowest FID score on CIFAR-10 respectively.

Figure 7.CelebA 64×64 generated results from different GAN loss functions.

Figure 8.BEGAN[50]generated results of dimension 128×128 on CelebA dataset.

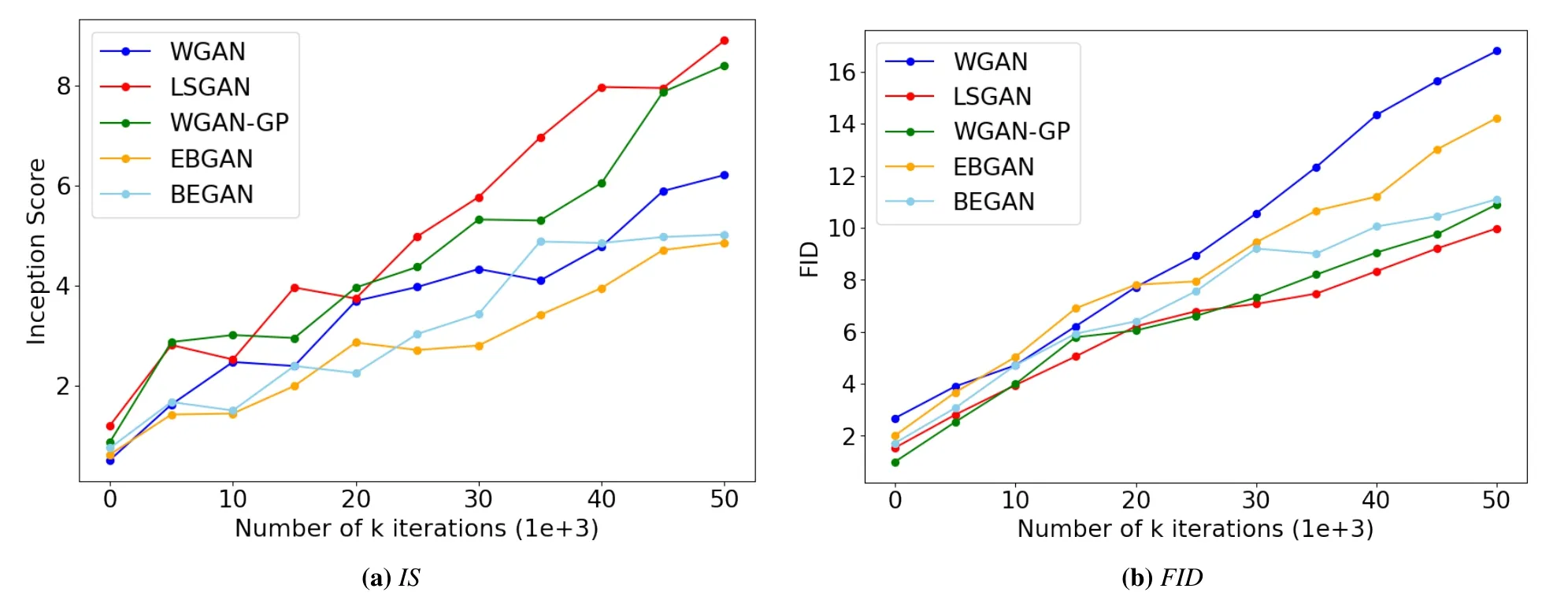
Figure 9.Inception and FID scores on CelebA dataset,LSGAN achieves the highest Inception and the lowest FID score on CelebA dataset.

Figure 10.MAD-GAN[38]generated 64×64 images on CelebA dataset from three different generators.

6.4 Generated Results of Multi-generator Networks

In Figure 10,the reported results of MAD-GAN using three generators[38]on CelebA dataset are shown.Figure 10(a)shows the generated 64×64 results by the first generator,Figure 10(b)shows the generated 64×64 results by the second generator,and Figure 10(c)shows the generated results by the third generator.It is notable in Figure 10 that the first generator generates images with dark background,the second generator generates images of female faces with light background,and the third generator generates images with colored background.In comparison with Figure 7 where WGAN,WGAN-GP,LSGAN,and EBGAN generate images of poor quality,the MAD-GAN generates images of high quality.However,similar to BEGAN in Figures 7(g)and 8 the generators of MADGAN generate images belonging to the female class more often than the images from the male class in CelebA dataset,hence the generators are unable to learn the inter-class variations of the real data distribution while focusing on intra-class variations of the real data distribution in CelebA dataset.We suggest the possible solution to this problem could be provided by combining the method of InfoGAN[27]with multiple generators of MAD-GAN,and feeding the latent code information along with the latent vectorzto the generators of the network.Some other multigenerator networks such as,MGAN[39]doesn’t provide qualitative comparison on CelebA dataset,however MGAN achieves the highet inception score on diverse dataset such as CIFAR-10,and large-scale datasets such as STL-10,and ImageNet[81],while E-GAN[47]show better diversity in generated images from CelebA dataset but show poorer quality than MAD-GAN[38].SGAN[63]achieves the highest inception score on CIFAR-10 dataset but the authors of SGAN exclude the qualitative and quantitative comparison on large-scale datasets.Therefore,there is no single GAN model that can generalize well on all the different datasets,specially in an unsupervised manner.However,despite the failure modes in generative modeling,GANs have achieved tremendous success and fame in different vision related tasks.Multi-generator and discriminator networks have been widely used to solve the problem of mode-collapse as discussed earlier in detail.In most cases,more than 2 generators,and up to 10 generators have also been used to generate fake samples.The idea behind using multiple generators in a single GAN model emphasises that the generated distributions of multiple generators would approximate the real data distribution,which somehow avoids the problem of mode-collapse by covering all the data modes.To achieve the diversity in the generated samples from multiple generators,the divergence between any two generators should be maximum,and the divergence between the mixture of all the generated distributions and the real data distribution should be minimum.However,adding multiple generators or discriminators in a single GAN model increases the complexity,computational cost,and increases the overall training process of the network.We observe that,in most of the multi-generator and discriminator networks,the quality of generated samples rarely improves on diverse large-scale datasets,and show little or no improvement in the quality of generated samples than a two-player generator discriminator network.

6.5 Suggestions on Choosing a Loss Function

Since considering the number of experiments we performed on GANs using different loss functions both qualitatively and quantitatively on three main image datasets,MNIST,CIFAR-10,and CelebA.We show that least square loss function(LSGANs)[31]outperforms all the other loss functions on evaluation metrics(IS and FID)except WGAN-GP in Figure 6,which achieves the highest inception score on CIFAR-10 dataset.However,analyzing the reported results by the authors of different GAN approaches in Table 5 we see that,all the variants of wasserstein loss and wasserstein loss with gradient penalty achieve the highest inception score and the lowest FID score on reported large-scale datasets such as,CIFAR-10 and LSUN,hence,it creates a room for uncertainty for the selection of a GAN loss function either for a general purpose or a particular task.To solve such uncertainty,we have to consider few points before choosing a particular loss function or a GAN architecture.First and most important,the architecture of a GAN framework.Second,the goal of the designed GAN framework and the nature of the task.Last but not least,the computational budget for the optimization of the designed GAN architecture.

So far,we have two best choices of loss functions for training GANs for both general purpose and specific tasks,the least square loss and wasserstein loss with gradient penalty.Least-square loss strictly penalizes the samples that are far from being real,which in turn solves the vanishing gradient problem in GANs.However,least square loss might generate some artifacts and extra-sharped images in vision specific task.Wasserstein loss on the other hand,not only provides useful gradients almost everywhere,but also improves the generating ability of a generator dramatically.However,Lucicet al.[82]argued that,if the computational budget and GAN model configuration for each loss function are kept same,then all the loss functions perform approximately the same and show network convergence.However,to reach such proximity of different loss functions towards network convergence,a huge amount of computational budget is required and model configurations to be the same,which is not an ideal situation considering limited resources and variety of different model configurations for different tasks.We suggest using wasserstein loss and its variants with gradient penalty,since wasserstein loss not only solves the vanishing gradient problem but also encourages the generator network to learn real data distribution,while stabilizing the training of the network and achieving optimal convergence.

Machine configurations.All the experiments were performed on Nvidia GTX 1080ti with 11G GPU memory on PyTorch and Python version 3.6,we use the deep convolutional DCGAN architecture[32]for training both the generator and discriminator networks.For training both the generator and discriminator networks according to different GAN approaches,we follow the official implementations provided by the authors of,WGAN[33],LSGAN[31],WGAN-GP[49],EBGAN[34]and BEGAN[50].For a fair comparison,we trained all the GAN methods on MNIST dataset in Figure 3 for 50 epochs each,and presented the corresponding evaluation scores in Figure 4.Similarly for CIFAR-10 dataset,we trained all the GAN methods for 50 epochs each in Figure 5 and presented the corresponding evaluation scores in Figure 6.Finally,on CelebA dataset,we trained all the GAN methods for 50Ktraining iterations each in Figure 7 and presented the evaluation scores in Figure 9.All the experiments on these three large-scale datasets took 72 hours in total to complete.

6.6 Applications and Future of GANs

GANs have been used in different tasks such as,generating photo-realistic photographs[83],generating faces of anime characters[84],image to image translation[3,5],text to image translation[85,86],semantic image to photo translation[6],face frontal view generation[87],generate new human poses[88],unsupervised cross-domain image generation[89],photograph editing[90,91],image de-raining[92],face aging[93],photo blending[94],photo inpainting[95—97],clothing translation[98],video prediction[99],and 3D object generation[100,101],image super resolution using Laplacian pyramid[102],overview of GAN-based image super resolution[103],face sketch to RGB image with edge optimization[104],detecting climate anamolies using GANs[105],traffic flow prediction using GANs[106].GANs have achieved significant progress in vision related tasks,however the common problems in GANs such as mode-collapse and vanishing gradient aren’t completely solved which makes a GAN model vulnerable during the training.Another problem is the computational cost,as a GAN model gets bigger the computational cost increases exponentially,unlike some smaller deep convolutional models that can be trained by using GPU with limited memory,the training of GANs,and specially the bigger GAN models require huge memory to train and that even doesn’t guarantee the stability of a GAN model.However GANs can be used in the field of medicine and its potential for drug discovery.Considering the vast applications of GANs,they can be utilized in different challenging fields such as,Blockchain[107],Big Data[108]and IoT systems[109,110].

6.6.1 Applications of GANs in other areas

Generative adversarial networks(GANs)can be successfully used in other promising fields besides visionrelated tasks,one such example is BitCoin(BTC).BitCoin is a digital currency and often described as crypto-currency,which is based on the shared peer-topeer technology of blockchain[107].Sample classification in Bitcoin is a challenging task,since the data entity classification in a supervised learning method heavily relies on the ground-truth dataset,and most ground-truth datasets contain class imbalance which may result in poor performance of a prediction model.However,GANs can be used to generate synthetic data to remedy class imbalance for Bitcoin-based data classification models[111].While,on the other hand,rapid development in the field of information presents challenges and interesting scenarios for information handling,data sharing,data analysis and data mining.All these data-related fields either from an industrial point of view or economical and social point of views can be handled using big data technology[108],one such application that combines both the generative adversarial networks and big data into a single deep learning based model for traffic flow prediction is GACNet[106],other such approaches that combine GANs and big data are,GANs for parallel transportation systems[112],generative adversarial networks for automated data generation[113],and GANs for missing view imputation in data analysis[114]etc.Generative adversarial networks can be used in IoT applications such as GAN-based slicing method for prediction and allocation of resources in IoT applications[115],and quantum technology and computation[116].

In summary,GANs can be successfully used for several tasks starting from vision-related tasks to big data,blockchain,IoT systems and many more.However,GANs aren’t a possible and a suitable fit to every problem,and the adversarial nature of GANs is quite sensitive to training data and selection of the suitable architecture.

To summarize Section VI,we presented the qualitative and quantitative analysis of different GAN approaches on three large-scale image datasets.We provided suggestions on choosing a suitable loss function for a GAN framework,we also provided the machine configurations or training details for GAN models.Furthermore,we discussed the vast applications and future directions of GANs in various promising fields yet not only limited to computer vision.

VII.CONCLUSION

In this paper,we have presented a survey of different GAN models and their corresponding loss functions in great detail.We have discussed the most common problems posed by GANs during network training such as,mode-collapse and vanishing gradient,and presented various solutions to avoid such issues.Not only we have discussed the loss functions of different GANs thoroughly,but we also presented pros and cons of these loss functions and suggestions on choosing a loss function for training GANs based on experimental evaluation.Despite the tremendous success of GANs,they still suffer from serious problems,the core idea behind this survey paper is to shed some light on such problems by reviewing existing solutions that are proposed to solve the problems faced by GANs.We have discussed applications and future of GANs in various fields starting from computer vision to other promising fields such as,blockchain,big data,and IoT systems.However,the problems posed by GANs such as mode-collapse,vanishing gradient and network instability are still far from being completely resolved.New loss functions,network optimization techniques and Network architectures are required to provide a wider range of solutions to solve these problems.Therefore,we encourage the future researchers to propose novel methods that address the problems in GANs by providing unique solutions,which can be extended to various other interesting and promising fields besides image processing and computer vision.