Code Design and Latency Analysis of Distributed Matrix Multiplication with Straggling Servers in Fading Channels

Ning Liu,Kuikui Li,Meixia Tao

1 School of Electronics,Information and Electrical Engineering,Shanghai Jiao Tong University,Shanghai 200240,China(email:ningliu@sjtu.edu.cn)

2 Huawei Technologies Co.,Ltd.,Shanghai 201206,China(email:likuikui1@Huawei.com)

3 Department of Electronic Engineering,Shanghai Jiao Tong University,Shanghai 200240,China

Abstract:This paper exploits coding to speed up computation offloading in a multi-server mobile edge computing(MEC)network with straggling servers and channel fading.The specific task we consider is to compute the product between a user-generated input data matrix and a large-scale model matrix that is stored distributively across the multiple edge nodes.The key idea of coding is to introduce computation redundancy to improve robustness against straggling servers and to create communication redundancy to improve reliability against channel fading.We utilize the hybrid design of maximum distance separable(MDS)coding and repetition coding.Based on the hybrid coding scheme,we conduct theoretical analysis on the average task uploading time,average edge computing time,and average output downloading time,respectively and then obtain the end-to-end task execution time.Numerical results demonstrate that when the task uploading phase or the edge computing phase is the performance bottleneck,the hybrid coding reduces to MDS coding;when the downlink transmission is the bottleneck,the hybrid coding reduces to repetition coding.The hybrid coding also outperforms the entangled polynomial coding that causes higher uplink and downlink communication loads.

Keywords:mobile edge computing;distributed matrix multiplication;coded computing;cooperative transmission

I.INTRODUCTION

1.1 Motivation

With the rapid growth of Internet of Things and artificial intelligence,massive new mobile applications are developed,such as online gaming,recommendation systems,virtual reality and augmented reality[1].These applications are in general computationintensive and delay-sensitive and expected to run at mobile users,whose computing and storage capabilities are restricted.To enable this,mobile edge computing(MEC)is deemed to be a promising network architecture that provides cloud-computing services at the edge nodes(ENs)of mobile networks[2—4].With MEC,these applications can be offloaded and executed on edge servers in close proximity to each user.

To complete a task offloading,the user needs to upload its local data to the ENs through the uplink channel.Then,the ENs carry out the computation on their servers,and return the computed results back to the user via downlink transmission.During this process,two performance bottlenecks may arise:first,the data delivery between the user and ENs may experience deep channel fading,which incurs low transmission rate and consequently causes long communication times in uploading the inputs or downloading the outputs;second,due to the existence of straggling edge servers[5],the time in waiting for the slowest ENs(i.e.,stragglers)to complete tasks is unpredictable.These factors will greatly increase the endto-end execution time for completing task offloading.It is thus highly necessary to alleviate the effects of deep fading and stragglers to speed up task offloading in MEC networks.

We consider a specific computation task,which is to compute the product between a user-generatedm×ninput data matrix X and a network-storedn×tmodel matrix A.Matrix multiplication is an essential operation in many machine learning and data analytic applications,e.g.,linear model-based inference operations[6].For instance,in collaborative filteringbased recommender systems[7],input X represents user profile vectors,model A is the profile vectors of the items,and the product results represent the ratings of the user to these items.Matrix A in general is of large scale,so it is stored distributedly across the ENs.This paper aims to exploit coding to introduce computation and communication redundancy to overcome straggling servers and channel fading,thereby speeding up distributed matrix multiplication in wireless environments.

1.2 Related Work

The idea of coding has shown significant benefits in distributed computing systems.It has been utilized in MapReduce frameworks to enable multicast opportunities in data shuffling to reduce the communication load[8—11].It is also leveraged to deal with the problem of straggling nodes in distributed systems.Compared to conventional approaches using task replication to tolerate stragglers[12,13],the coding approach provides better robustness to stragglers since it needs less number of non-stragglers to recover the output.Specifically,the maximum distance separable(MDS)code is applied in[14]for distributed matrix multiplication in master-slave systems.By assigning the MDS-encoded row vectors to each worker for computation,the original matrix product results can be recovered from the coded outputs computed on the nonstraggling nodes.The works[15—17]extend the MDS coding approach to MapReduce frameworks to solve the straggler problem.

In the aforementioned literature[14—17],coding is only applied to one matrix,while the other matrix in the multiplication is assumed to be small enough to store on all workers.The works[18—20]consider the scenario in which both multiplication matrices are large and each worker is only able to store part of each matrix.Improved coding schemes are then proposed to encode both matrices.In specific,the work[18]proposes the product coding scheme that encodes the two matrices by using two-dimensional MDS codes.Nevertheless,this scheme still needs a large number of nodes to finish tasks in order to recover all outputs.To reduce the recovery threshold,the polynomial coding scheme is proposed in[19],which splits both multiplication matrices into submatrices either along the row side or along the column side,and then encodes the submatrices by using the polynomial code.Furthermore,the authors in[20]improve this scheme and propose the entangled polynomial coding scheme,which allows the two multiplication matrices to be split along both row and column sides.By this scheme,the original matrix multiplication can be represented as the sum of the products of the split submatrices,which can be recovered from less number of coded outputs.So the recovery threshold is further reduced.However,in this coding scheme,since each worker is assigned distinct coded submatrices,the traffic load caused by task assignment grows linearly with the number of workers.Moreover,the dimension of the product of two coded submatrices may be as large as that of the uncoded scheme,leading to a large communication overhead for returning outputs to the master.

Nevertheless,these works[14—20]on coded computing only focus on distributed computing where the data exchange among different nodes is assumed to be error-free.In MEC networks,task offloading is also affected significantly by the severe channel fading and interference in wireless environment.Recently,there have been extensive works on task offloading strategies and resource allocation to optimize the performance of MEC in wireless environment,such as[21—27].These works,however,are often limited to the scenario where a user task is computed once on a single EN only.As such,no communication or computation redundancy can be exploited to mitigate channel fading(or interference)and straggling nodes.There are also works on coded computing in MEC networks to speed up both task computation and data transmission processes,such as[28,29].In particular,the work[28]utilizes coded computing to overcome the straggling servers in MEC networks.It is shown that the computation redundancy injected by coding also allows multiple ENs to cooperatively transmit their common output data to the user by using zero-forcing(ZF)precoding,as in[30—34]for coded caching and computing in wireless interference networks.Note that[28]assumes that the input data of all users is available at all ENs in advance with task uploading cost ignored.The work[29]develops a more comprehensive coding approach by jointly optimizing the task uploading,edge computing,and output downloading phases,and characterizes the fundamental tradeoffs among uploading,computing,and downloading times.It is shown that a hybrid MDS and repetition coding can deal with the straggling servers and also enable cooperative interference management.Note that the latency-oriented performance analysis in[28,29]is conducted from the informationtheoretically asymptotic perspective in the high signalto-noise ratio(SNR)regime,and the EN cooperation is mainly to eliminate the co-channel interference and hence maximize the multiplexing gain.As a result,no direct conclusion is given to the exact communication and computation latency.

1.3 Contribution

We consider the code design and end-to-end latency analysis for distributed matrix multiplication in a single-user multi-server MEC system.Coding is used to generate computation and communication redundancy at the ENs so as to provide robustness against stragglers and overcome the deep fading.More specifically,by applying linear coding to encode the network-stored model matrix A and uploading the associated user input submatrices to their corresponding subsets of ENs,the ENs compute linearly encoded vector products,from which the original product result can be recovered due to the linearity of matrix multiplication.Moreover,the communication redundancy allows multiple ENs with the same outputs to cooperatively transmit the common data to the user.Unlike[28,29],we consider the exact end-to-end task execution time as the performance metric,and our considered EN cooperation is to mitigate the channel fading and thus achieve the diversity gain[35,36].

We adopt the similar hybrid MDS-repetition coding scheme as in[29]for the considered wireless distributed matrix multiplication.More specifically,the input matrix X generated by the user is partitioned into multiple submatrices,and each is assigned to a subset of ENs for computation;the model matrix A is encoded by a cascade of MDS code and repetition code,and then stored distributively across the ENs.Each EN computes the coded submatrix product results.The MDS code ensures that the desired output can be recovered from a give number of completing ENs,so as to increase robustness against stragglers.The repetition coding,on the other hand,enables multiple ENs to transmit cooperatively in the downlink to mitigate the channel fading.The code rates in the hybrid MDSrepetition coding approach are design variables to be optimized.

Based on the above task assignment,edge computing,and result downloading scheme,we provide a rigorous analysis on the average end-to-end execution time.We show that using the proposed scheme,the uplink is formed as a multicast channel while the downlink is a MISO channel.We analyze their ergodic rates,and derive the task uploading,computing,and downloading times,respectively.The analytical expression of the end-to-end execution time is then obtained.For comparison,we also derive the endto-end execution time for three benchmark schemes based on MDS coding,repetition coding,and entangled polynomial coding,respectively.In particular,the MDS coding and the repetition coding are the special cases of the hybrid MDS-repetition code,and the entangled polynomial coding is a generation of the coding scheme from[20].

We carry out simulation to validate the theoretical latency analysis.Numerical results show that the hybrid coding always outperforms the benchmark schemes.The hybrid coding scheme can utilize both the robustness of MDS coding to overcome stragglers and the duplication brought by repetition coding to enable transmitter cooperation to mitigate channel fading.In contrast,the entangled polynomial coding causes the large total time due to the needed higher uplink and downlink communication loads.

The remainder of this paper is organized as follows.Section II presents the MEC network model and performance metric definition.The coding schemes and latency analysis are detailed in Section III.Section IV provides numerical results.Conclusion is given in Section V.

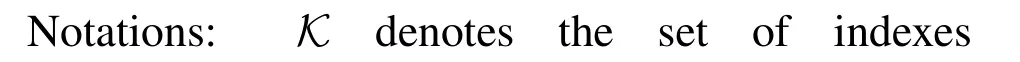
Table 1.List of important notations.

II.SYSTEM DESCRIPTION

2.1 MEC Network Model

We consider an MEC network,as shown in Figure 1,where a single-antenna user has an input data to be offloaded toKsingle-antenna ENs for distributed com-

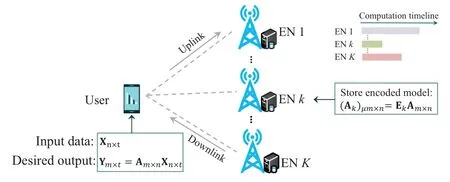
Figure 1.A K-server MEC network where the user offloads the distributed matrix-multiplication task through input uploading,edge computation,and output downloading.

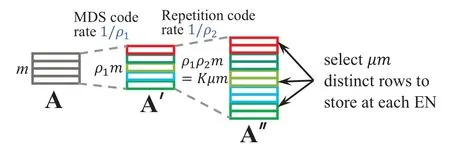
Figure 2.Illustration of hybrid MDS-repetition coding[29].

2.2 Performance Metric

To carry out a task computation,the user first makes a task assignment policy to decide which input vectors are assigned to each EN.Then,it uploads the input vectors to the corresponding ENs via the uplink channel.After waiting for a certain number of ENs to finish their tasks,the user downloads the computation results from these ENs through downlink channels.Note that the received coded outputs must contain enough information to recover all the outputs.Then,the user employs the corresponding decoding function to decode the desired outputs[39].

We characterize the network performance by the average end-to-end execution timeT,which is defined as the sum of the average input uploading timeTu,average edge computing timeTc,and average output downloading timeTd,i.e.,

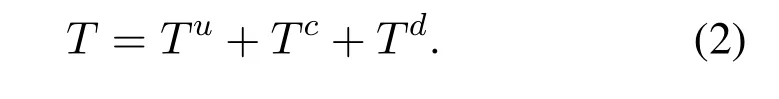
Here,for simplicity,the encoding and decoding time is omitted in this paper,as in[15,16,28,29].In the next section,we present the detailed coding and task offloading schemes,and derive their average end-toend execution time.

III.CODING SCHEME AND PERFORMANCE ANALYSIS

In this section,we first utilize the hybrid MDSrepetition coding for distributed matrix multiplication in MEC networks.Then,we consider three benchmark schemes based on the MDS coding,repetition coding,and entangled polynomial coding,respectively.We consider the general SNR regime and analyze the average uploading time,computing time,downloading time,as well as end-to-end execution time,of these schemes.

The common idea of different coding schemes is to introduce computation redundancy to reduce the number of ENs that need to finish their tasks for output recovery and also enable transmission redundancy to overcome channel fading for result downloading.

3.1 Hybrid MDS-repetition Coding Scheme

In this scheme,we integrate the hybrid MDS and repetition coding strategy with the transmitter cooperation technique,as detailed below.Note that the similar coding scheme has been applied in[29]but the difference is that the EN cooperation in[29]enabled by coded computing is to achieve the multiplexing gain rather than the transmit diversity gain considered in our work.Moreover,the latency analysis in[29]is carried out from the information-theoretically asymptotic perspective in the high SNR regime,while this work analyzes the exact transmission and computation times in the general SNR regime.

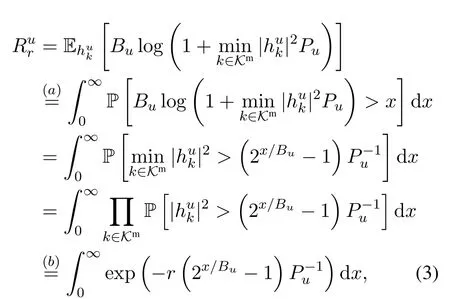
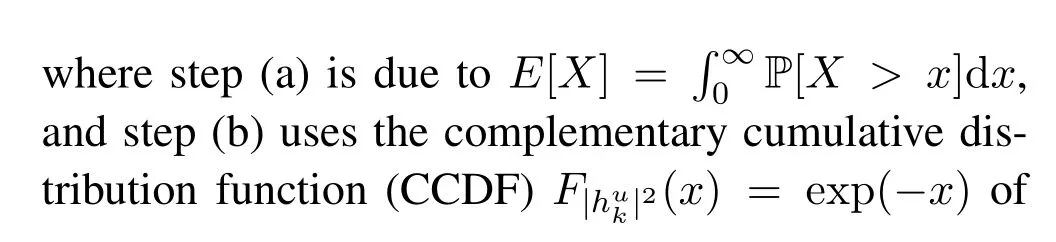
Due tor-(K-q)≤p1≤min{r,q}andlp1－1≤p2≤min{p1,ρ2},whenrandqincrease,both the lower and upper limits of the interval ofp2increase.Namely,the number of ENs for cooperative transmission increases.Thus,the downloading timeTd(r,q)will decrease.Recall thatTu(r)andTc(r,q)increases withrandq.As such,there exist tradeoffs among uploading,computing,and downloading times.

We use the example in Figure 3 to explain the output downloading scheme.Consider input x1assigned top1= 2 non-stragglers,its outputs{a25x1,a26x1,...,a30x1}in the red dashed rectangle is computed repeatedly onp2=2 non-stragglers.Thus,the downlink is a MISO channel,and these outputs can be returned by using transmit diversity technique.For the rest outputs in the blue rectangle,each is computed onp2= 1 non-stragglers,the resulting downlink is a point-to-point channel,and these outputs is returned via TDMA.Similarly,for input xi,i ∈[2 :5],their outputs can be divided into multiple groups to be transmitted,each group with the same degrees of replication.

Figure 4.Example of entangled polynomial coding in task offloading:K=4,μ=1/2,and dc2+d-1=3.

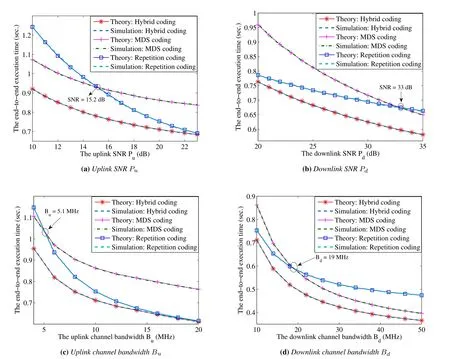
Figure 5.The impacts of the uplink and downlink channel SNRs and bandwidths on the end-to-end execution time.

End-to-end time:By summing up(4),(6),and(10),the average end-to-end execution time at given repetition orderrand recovery orderqis obtained.Based on the recovery condition discussed above,a feasible set of(r,q)is given as

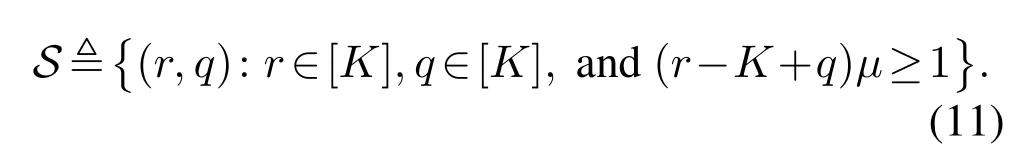
By optimizing(r,q),the minimum average end-to-end execution time is given as

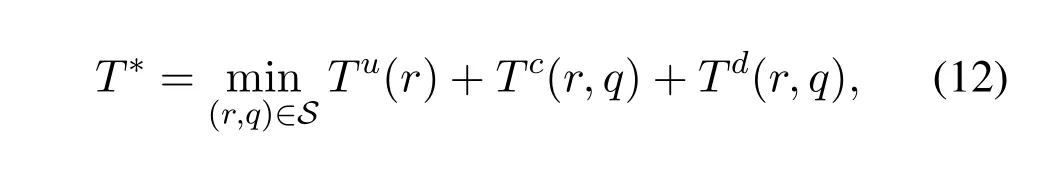
whereS,Tu(r),Tc(r,q),andTd(r,q)are given in(11),(4),(6),and(10),respectively.According to the impact of(r,q)on the three latency components,we have the following remark.

Remark 1.The large repetition order r and recovery order q will cause more uploading time Tu(r)and computing time Tc(r,q).This is because in uploading phases,more data traffic is uploaded to ENs,and in computing phases,the system will wait for more ENs to finish tasks.Nevertheless,this in turn can decrease the downloading time Td(r,q)since there are more transmission cooperation opportunities to be utilized.Therefore,by optimizing the parameters r and q,we can balance the three latencies to achieve the minimum end-to-end execution time.

3.2 MDS Coding Scheme

This scheme only uses MDS code to encode matrix A,which is the special case of the hybrid scheme whenρ1=Kμandρ2=1.Given(r,q)∈S,for the MDS coding scheme,the average uploading timeTu(r)and computing timeTc(r,q)are still given in(4)and(6),respectively,which are not affected by coding rates.For output downloading scheme,due toρ2= 1,we havep2=1,so each product of submatrices is computed on one EN only,and no cooperation gain can be utilized in downlink transmission.The average downloading time in(10)reduces to

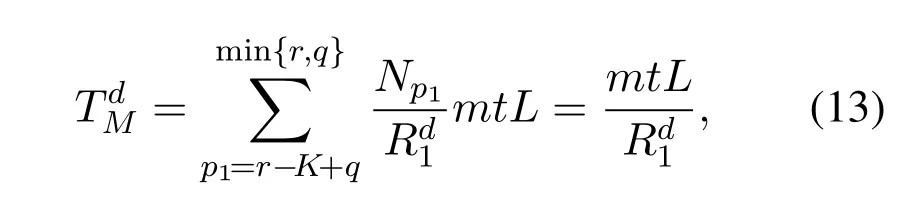
which is independent ofrandq.The minimum endto-end execution time is given as

Remark 2.As a special case of the hybrid coding,the MDS coding causes larger downloading times since it cannot utilize transmitter cooperation,while it can reduce uploading and computing times by improving the robustness against stragglers.

3.3 Repetition Coding Scheme

Remark 3.The repetition coding,as another special case of the hybrid coding,causes larger uploading and computing times since it cannot provide the same robustness against stragglers as the MDS coding;while it can reduce the downloading time by improving the transmission cooperation.

3.4 Entangled Polynomial Coding Scheme

Remark 4.Observing(22),(23),and(24),we see that the advantage of the entangled polynomial coding is to reduce the number of needed outputs to recover the product results.However,since each worker is assigned distinct coded submatrices,the uplink traffic load grows linearly with the EN number;moreover,the dimension of the product of 2 encoded submatrices may be as large as that ofAX,causing a large downloading time for returning outputs.

IV.NUMERICAL RESULTS

In this section,we provide numerical examples to evaluate the performances of the proposed task offloading policies based on hybrid MDS-repetition coding,MDS coding,repetition coding,and entangled polynomial coding,respectively,in terms of the end-to-end execution time.

We consider a 10-server MEC network,where each EN can storeμ=3/5 fractional rows of dataset matrix A.A hasm=5000 rows andn=1000 columns,and the user’s input matrix X hasn=1000 rows andt=1000 columns.The size of each element isL=8 bits.Consider the normalized noise power,the uplink and downlink channel SNRs equal toPu=20 dB andPd=23 dB,respectively.The uplink and downlink channel bandwidths areBu=Bd=10 MHz.The mean of the random time for each EN to compute a product of two elements is 1/η=10－9seconds.ηalso indicates the average number of element products that each EN can compute per unit time,i.e.,the average computing speed of each EN.The simulations are averaged over 50000 independent channel realizations.

We first illustrate the performance of hybrid MDSrepetition coding in comparison with its two special cases,namely,pure MDS coding and pure repetition coding.Figure 5 illustrates the impacts of the communication parameters including the uplink and downlink channel SNRs and bandwidths on the end-to-end execution time.It is seen that the simulation results are well consistent with the theoretical results.The hybrid coding scheme always outperforms MDS coding and repetition coding schemes,no matter how the parameters change.This is because the hybrid coding scheme can not only utilize the robustness of MDS coding to overcome stragglers in computing phases but also use repetition coding to create more duplicated outputs for transmitter cooperation in downlink.Thus,it reduces the total time significantly.

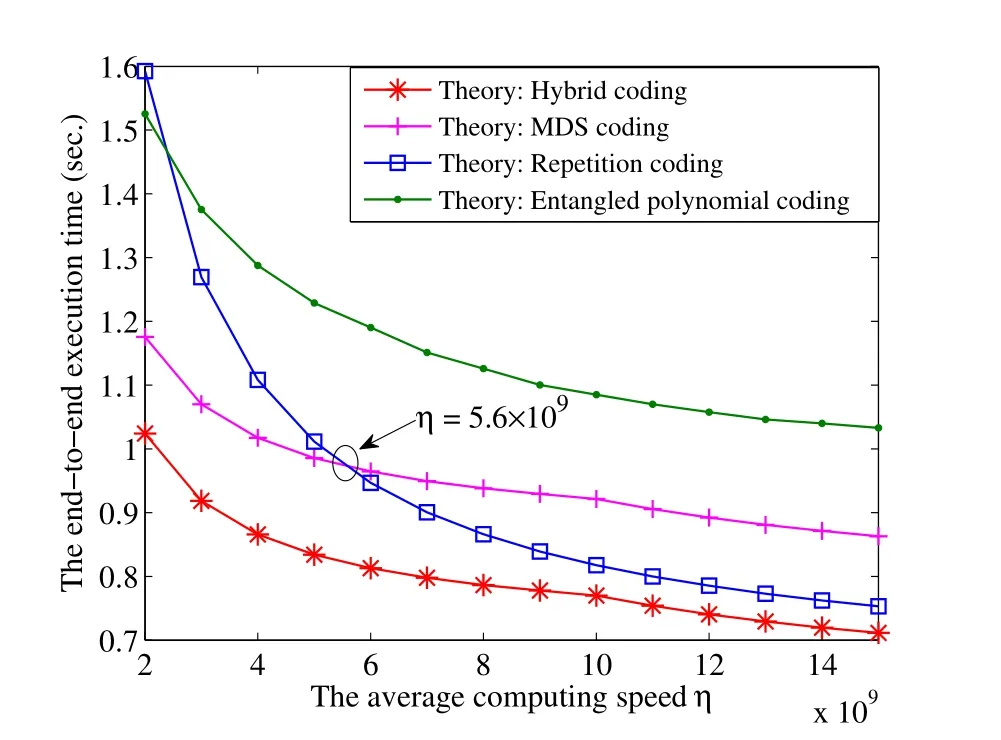
Figure 6.The end-to-end execution time versus the mean of the EN computing speed η.

In Figure 5(a),it can be observed that as the uplink SNR increases,the task offloading time of repetition coding scheme decreases faster than other schemes,since the higher SNR reduces the uplink communication overhead and thus highlights the advantage of repetition coding in realizing downlink cooperation to decrease downloading times.WhenPu ＞15.2 dB,repetition coding performs better than MDS coding,and it gradually approaches the hybrid coding scheme.In contrast,in Figure 5(b),the time achieved by repetition coding decreases very slowly when the downlink SNR increases.In this case,the task offloading process is gradually not limited by the downlink communication,so the gain of repetition coding is limited,and its robustness against stragglers is weaker than the MDS coding.WhenPd ＞33 dB,the gain of MDS coding exceed that of repetition coding.AsPdincreases,the downlink transmission rate is high enough,so the bottleneck is from the input uploading and edge computing phases;the hybrid scheme gradually reduces to the MDS coding,since MDS coding needs less number of ENs to recover all outputs,which relaxes the constraints for input uploading and EN computing.

The impact of uplink and downlink channel bandwidths on the end-to-end execution time is shown in Figure 5(c)and Figure 5(d),which are similar to that of uplink and downlink SNRs.As the uplink bandwidthBuincreases,the offloading time of repetition coding scheme decreases rapidly;while,as the downlink bandwidthBdincreases,the time decreases very slowly.We also see that whenBu ＞5.1 MHz orBd ＜19 MHz,repetition coding can exploit more transmitter cooperation gain in downlink since the total time is limited by the downloading time;whenBu ＜5.1 MHz orBd ＞19 MHz,the offloading process is limited by uplink communications,so the MDS coding gradually approaches the best scheme.

Now we illustrate the performance of hybrid MDSrepetition coding in comparison with all the benchmarks,including the entangled polynomial coding.Figure 6 and Figure 7 demonstrate the impacts of the computation parameters including the average computing speed of each EN and the output data size on the end-to-end execution time.It is seen that the hybrid coding outperforms the entangled polynomial coding;and in most cases,the entangled polynomial coding achieves the largest end-to-end time among the three benchmark schemes.As stated in Remark 4,this is because for the entangled polynomial coding,the data traffic to be uploaded grows linearly with the number of participating ENs,and the dimension of the product of two coded submatrices may be very large,resulting in large upload and download times.

In Figure 6,whenη＜5.6×109,i.e.,the average EN computing speed is slow,the repetition coding scheme causes larger computation times since it needs more non-stragglers to finish tasks,while the MDS coding can significantly decrease the computing time due to the required less number of non-straggling ENs.Whenη ＞5.6×109,the EN computing speed is no long the bottleneck,so the gain of repetition coding in downlink communications increases,and its performance is close to the hybrid scheme whenηis sufficiently large.

In Figure 7,we see that compared to other parameters,the output data size has a stronger impact on the system performance,and the end-to-end execution time grows almost linearly with it.Similar to the impact of downlink SNR and bandwidth,when the output data size is small,e.g.,mtL＜2.05×107bits,the output downloading is not the bottleneck that causes more times,so the gain of repetition coding is limited;whenmtL ＞2.05×107bits,the proportion of downloading times in the total time is large,so repetition coding brings more cooperation gains in downlink,and hence it approaches the hybrid coding scheme for very large output data size.

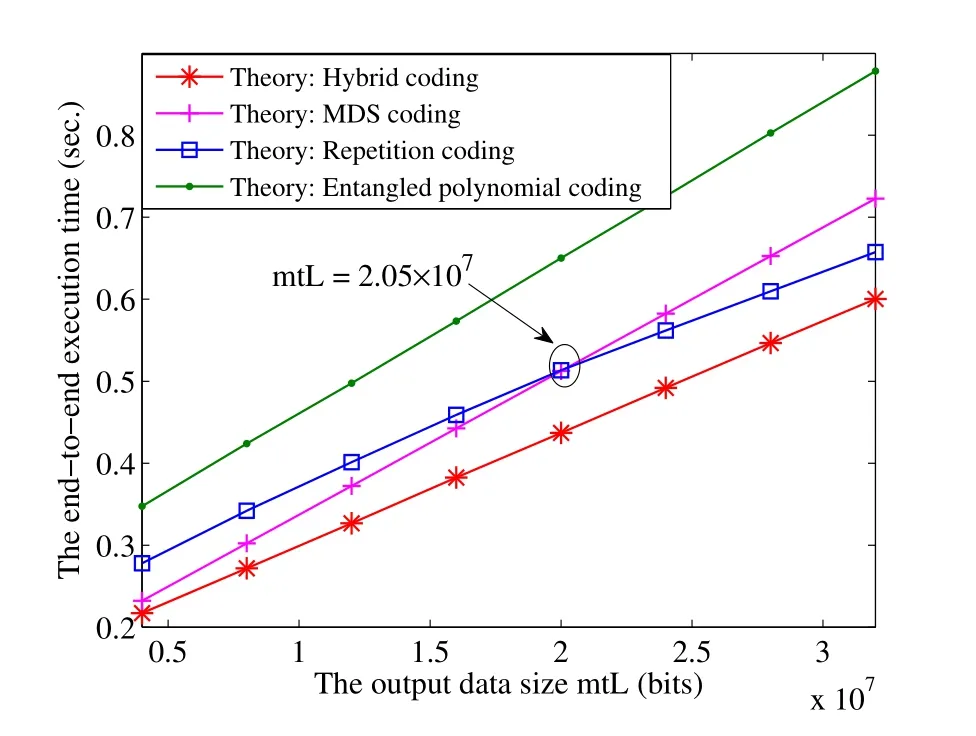
Figure 7.The end-to-end execution time versus the output data size mtL.

V.CONCLUSION

This paper exploits coding for the distributed matrixmultiplication task in the MEC network with stragglers and channel fading.We utilize the hybrid MDS-repetition coding and cooperative transmission in task offloading.By introducing hybrid coding to the network-side model matrix,the computation redundancy is created on the ENs,which can be leveraged to overcome the random stragglers and realize transmitter cooperation for mitigating the channel fading.Then,the average end-to-end execution time is derived.We also consider three benchmark schemes by applying MDS coding,repetition coding,and entangled polynomial coding,respectively.Numerical results show that when the downlink transmission is the bottleneck of the offloading process,the hybrid coding reduces to repetition coding to bring more diversity gain in downlink;when the offloading process is limited by the uplink transmission or edge computation phase,the hybrid coding reduces to MDS coding to reduce input uploading time and provide better robustness to stragglers.The hybrid coding also outperforms the entangled polynomial coding.

Note that this work has focused on matrix multiplication,which is a specific computation task but also serves as a building block for many machine learning and data analytics tasks.Code design and performance analysis for more complex computation tasks in MEC networks with both stragglers and channel fading can be investigated in the future work.

ACKNOWLEDGEMENT

This work is supported by NSF of China under grant U1908210 and by National Key R&D Project of China under grant 2019YFB1802702.

APPENDIX