考虑砂岩残余强度的二元结构深挖路堑边坡稳定性分析

叶帅华, 樊黎明, 时轶磊

(1. 兰州理工大学 甘肃省土木工程防灾减灾重点实验室, 甘肃 兰州 730050; 2. 兰州理工大学 西部土木工程防灾减灾教育部工程研究中心, 甘肃 兰州 730050)

在中国西部地区高等级公路的建设过程中出现了大量的边坡工程，这类边坡工程往往具有纵断面长、横断面宽、坡高极高、工程量巨大的特点，因此在施工及后期运营过程中常常会发生失稳现象，对国家财产和人民生命安全带来严重威胁.许多学者针对我国西部地区边坡工程中出现的问题进行了研究，谢永利等[1]通过离心机试验与有限元软件模拟全面分析了黄土公路阶梯状高路堑边坡的变形发展过程、破坏特征及其稳定性.王玉峰等[2]以观音堂隧道进口明洞段黄土高边坡为实例，利用离心机试验对黄土高边坡在无支护、全断面土钉支护、上部土钉下部预加固桩复合支护模式下的稳定性展开研究，并分析了各类支护形式对黄土边坡的加固效果.朱彦鹏等[3]采用FLAC 3D有限差分程序对黄土地区隧道进口段进行三维动态施工分析，研究了不同开挖方式对洞口未支护及已支护边坡的的影响.王邓峮等[4]针对黄土地区常见的土钉复合锚杆支护结构建立附加应力作用下边坡的稳定性分析模型从而区分了土钉与预应力锚杆的作用.谷天峰[5]则通过不排水动三轴试验模拟了列车荷载对黄土边坡的变形过程和稳定性的影响.叶帅华等[6]采用集中质量法并考虑预应力锚杆动力特性建立了框架-预应力锚杆-土体系统在地震作用下的动力计算模型，并基于此模型分析了格构锚杆支护边坡的地震响应.

虽然对西部地区边坡工程的研究已取得了许多成果，然而这些研究多数是针对西部地区黄土边坡的研究.随着西部经济建设的发展和需要，公路向山区纵深发展，使得路堑边坡开挖深度越来越大，在公路修建过程中出现大量黄土-砂岩二元结构边坡 ，这在甘肃省的公路建设工程中体现得尤为明显.目前，对红层边坡工程所展开的研究多集中于我国南方，对甘肃地区公路工程中出现的砂岩边坡工程研究较少，其研究内容也仅限于对红层边坡的变形监测[7].但是近年来在甘肃地区由砂岩引起的工程病害却相当严重，以G316线甘肃省境内稍子坡段为例，该标段全长为6 km，公路路基全为第三系红砂层软岩，路基完工后发生7处大型滑坡[8].因此，对甘肃省境内涉及砂岩层的公路而言，其关于边坡稳定性的研究就显得尤为迫切.

目前，在公路路堑边坡支护设计及其稳定性分析中，对于岩土体材料是应该采用残余强度还是峰值强度并没有明确的结论.大多数学者认为采用材料的残余强度进行支护和稳定性分析过于保守，然而，王骑虎[8]在对甘肃红层力学性质全面研究的基础上，认为应采用岩体残余强度对覆盖型红层边坡进行稳定性分析.文献[9，10]在对砂岩力学性质进行深入研究后指出砂岩的力学性质与其应力水平、围压的加卸载速度密切相关.王瑞红等[11]在研究卸荷对砂岩力学参数的影响及卸荷过程中岩体力学参数的变化规律时指出，与加载破坏相比，卸荷破坏时岩样强度对围压更为敏感.陈晓平[12]通过对一实际软岩边坡的稳定性分析，指出此类边坡的设计与分析必须考虑卸荷松弛所导致的土体强度的衰减.由此可见对于深挖砂岩路堑边坡，其岩土材料强度参数的选取仍是一个值得探讨的问题.本文将以兰永一级公路K35+000～150标段失稳黄土-砂岩二元结构高边坡为背景，基于边坡的极限平衡状态采用GeoStudio岩土有限元软件分别采用峰值强度及残余强度对该边坡的稳定性进行分析，并在残余强度的基础上对采用框架预应力锚杆加固后该边坡的稳定性进行分析，以便为今后甘肃红层地区的公路建设提供参考.

1 边坡工程概况

1.1 地形地貌特征

兰永一级公路项目地处陇西黄土高原的西北部，是黄土高原与青藏高原的过渡地带，区内沟谷纵横，地形起伏较大，大部分地区为黄土覆盖，山区一般为基岩出露.其中K35+000～150标段所处区域地貌形态为黄土丘陵，属雾宿山余脉，山体陡峭，植被稀少，侵蚀强烈，沟谷相间，沟壁较陡、谷底狭窄.基底为白垩系红色粘土岩、砂岩和砂砾岩；局部受断层影响，出露前震旦系片岩、中上奥陶统变质安山岩、千枚岩及变质砂岩以及侵入石英闪长岩，上覆黄土.

1.2 工程地质条件

根据地质调查，K35+000～150标段右侧深挖路堑边坡为砂岩上覆黄土边坡，开挖坡体地层可分为四层，自上而下分别为：1) 上更新统风积黄土，可塑—硬塑状，土质均匀，孔隙多见，具强湿陷性；2) 下伏为冲积黄土，黄褐色，干燥，硬塑状，土质均匀；3) 冲积砾石层，青灰色，稍密—中密，砂土填充，厚3～6 m；4) 下白垩统河口群砂岩，紫红色，泥质胶结，成岩性较好.

1.3 气候与水文条件

该公路项目所经地区为永靖和兰州.永靖位于内陆中纬地带，大陆性气候显著，属温带半干旱偏旱气候类型，降雨主要集中在7～9三个月，季节变化大，局部山地降水较大.兰州地处我国内陆腹地，距海洋较远，属大陆性季风、半干旱气候区，降水主要集中在7～9三个月内，约占全年降水量的60%以上，且多以暴雨形式降落.兰永线沿线河流属黄河流域，主要河流为黄河、湟水河、庄浪河和咸水河.

1.4 边坡破坏过程及其特征

失稳的开挖边坡为砂岩、黄土二元结构边坡，岩土交界面夹6 m卵石层，采用2 m宽碎落台，2 m宽挖方平台；该边坡第一级坡率0.5，10 m高(采用锚索框格梁防护)，第二级坡率0.5，8 m高(采用锚杆框格梁防护)，二级坡坡顶有6 m宽平台(岩土交界面)；第三、四级坡率0.75，三级边坡采用孔窗式护面墙防护卵石夹层，四级坡顶平台宽4 m；第五级坡率1，挖方平台设平台排水沟.截至2013年9月路堑开挖基本成形，路槽达到设计标高，原设计边坡防护未施作.2013年9月中旬，K35+000～150段山体开始出现裂缝，经过观察，裂缝在进一步发展.9月25日，截水沟上部裂缝最宽处已经达到18 cm，开裂长度约50 m，并且已经施工完毕的路基边坡平台、孔窗式护面墙都出现了开裂；2013年9月28日下午4时，山体突然出现较大面积滑塌，黄土路堑坡口处下错6～10 m，黄土坡体整体变形，底部砂岩压溃，开挖路床中线位置有明显破坏剪出痕迹.最外缘裂缝出现于原有开挖坡口位置，坡体后缘无张拉裂缝.

2 边坡失稳机制分析及参数选取

2.1 边坡失稳原因分析

该路堑边坡下部出露地层为下白垩统河口群砂岩夹泥岩，抗风化能力差，遇水易崩解.当其处于深埋状态时，裂隙发育不充分，成岩性较好，但由于基岩上覆土层竖向节理发育，开挖时段又恰逢该地区多雨时节，基岩在顶部雨水浸泡下逐步软化，而在开挖过程中，由于未作任何护坡措施，卸荷松弛和岩层风化进一步造成边坡底部砂岩强度衰减，此外，在对底部岩层进行削坡时，临空面扩大，坡体底部失去支撑，加之岩层上覆黄土层厚度及土压力大，最终使得坡底软岩被压溃，基岩上部覆盖黄土层也随之产生滑塌，导致整个边坡发生失稳破坏.由此可见，环境影响以及开挖卸荷导致的应力释放均会削弱砂岩强度，使二元结构边坡向极限状态缓慢过度，最终发生破坏，因此有必要对砂岩二元结构深挖路堑边坡稳定性分析中所采用的基岩强度参数进行合理的探讨.

2.2 边坡数值模型

基于K35+000～150段的边坡工程地质条件，考虑现场边坡完工时的开挖形态，采用GeoStudio岩土有限元软件中的SLOPE模块建立图1所示的数值模型.该平面模型以该标段中的 K35+054为典型断面(如图2所示)，该断面高度38.45 m,其中一级坡高10 m，二级坡高8m，三～五级每级坡高6 m，一、二级坡率为1∶0.5，三、四级坡率为1∶0.75，五级坡率为1∶1.

图1 边坡数值模型图

图2 边坡地形剖面(mm)

数值模型右侧边界取至自然斜坡坡顶，左侧边界取该标段公路中心线处，模型两侧均采用竖向滑动支座进行约束，底边界采用固定支座.整个模型开挖按实际工况分15个步骤，阶段1为生成初始应力步，阶段2～阶段15对应实际开挖步，每级开挖高度在2～3 m之间.

2.3 岩土力学参数选取

1937年，Tiedeman首次提出残余强度的概念[13].在边坡发生滑动时，常常发现滑动面上的平均剪应力比它们的抗剪强度小的多[14].Skempton等[15]在对黏性斜坡的长期稳定性进行研究时将这一强度定义为残余强度,并强调残余强度对滑坡的稳定性起控制作用.对于边坡工程而言，在其设计过程中通常按极限平衡状态分析边坡稳定性，此状态下，坡体内已基本形成贯通边坡的滑移带，剪切破坏面之间已产生相对滑动的趋势或已经出现相对滑动.此时，边坡的稳定性通过剪切破坏面之间岩土体残余强度来决定，但由于相关规范并没有明确边坡设计过程中究竟采用何种材料强度，因此设计人员也极少按岩土材料残余强度参数进行极限状态设计.此外，实际工程中，边坡受环境及卸荷松弛的影响，岩体强度参数已经有所衰减，而路堑边坡工作环境恶劣且为永久性边坡，在自然环境下其强度会进一步降低，此时若继续依据峰值强度进行稳定性分析则可能使设计的边坡在开挖完成一定时间后发生滑塌.因此从稳定性分析概念以及实际工程安全性角度出发，采用残余强度进行边坡稳定性分析应该更符合实际.

张芳枝[16]在浸水软化后对东深供水工程沿线边坡砂岩土样进行反复直剪试验确定砂岩残余强度约为峰值强度的70%.王骑虎[8]采用反复剪切试验对兰永一级公路及十天公路沿线14组扰动砂岩土样浸水后的残余强度进行研究，其研究结果与文献[16]基本一致.因此，本文在研究不同强度条件下的边坡整体稳定性时，采用有限元极限平衡法分别对下述2种工况进行分析和比较.工况 1：采用边坡各岩土层的天然峰值强度指标；工况 2：根据地质条件相似性以及兰永线红砂岩反复剪切试验结果[8]，将砂岩峰值强度折减70%.工况1岩土层主要力学参数见表1.

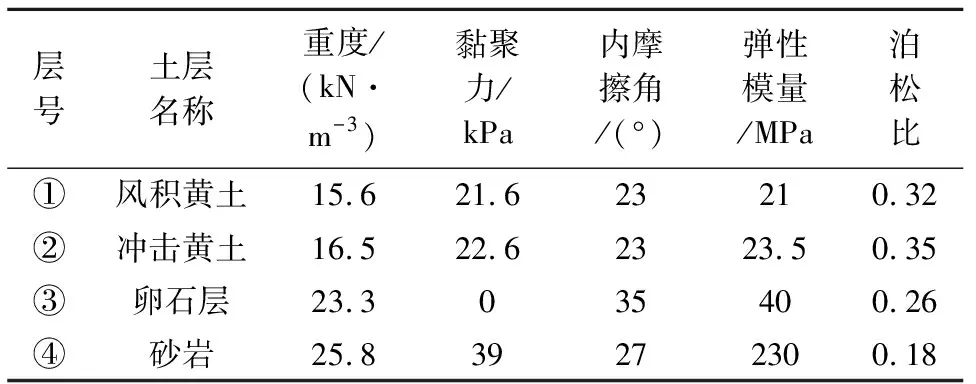
表1 工况1岩土层力学参数Tab.1 Soil parameter table of working condition one

3 边坡模拟分析

3.1 边坡稳定性分析及其稳态变化

边坡有限元极限平衡法是指在弹塑性有限元分析结果的基础上，以极限平衡条件作为判别准则对边坡进行稳定性分析的方法，其优势在于分析过程中的滑动面是基于有限元分析中的真实应力场所得到的，因而不需要对条间力作任何假设[17].本文通过将有限元分析软件GeoStudio中SIGMA模块与SLOPE模块进行耦合，在峰值强度与残余强度的基础上分别对该边坡的安全性系数进行了模拟分析，模拟结果分别如图3～5所示.

图3 工况1边坡安全系数云图Fig.3 Safety factor nephogram of slope under working condition one

两种不同强度指标计算的结果显示，无论边坡岩体处于何种强度下，边坡安全系数较小值都集中在距离坡面较近的深度范围内，呈带状分布，并逐渐由该条带向两侧增大.但对比不同强度下的边坡开挖完成后的最小安全系数可以看到，当采用岩体峰值强度进行计算时，该边坡最小安全系数为1.271，按相关规范[18]判定该边坡处于基本稳定状态，与边坡实际发生破坏的状况不符，而当采用残余强度指标进行计算时，边坡最小安全系数骤减至0.901，处于不稳定状态.对图3、图4的安全系数云图进一步的对比分析可以看到当边坡底部砂岩处于残余强度阶段时，安全系数在1.001～1.201范围内的土体滑动面从坡顶后缘处一直延伸至坡脚前缘，说明在该强度下，边坡还有可能会因砂岩强度不足而发生较大范围的整体失稳并造成道路路面的破坏，这与现场勘查的实际状况相一致.由此可见采用残余强度对边坡进行极限状态下的稳定性分析更贴合实际工程.

农业生产过程中，由于农民群众连续在一个地块种植同一种农作物，施肥不注重有机肥施入，化肥尤其是氮肥施入过多，导致土壤理化性质发生严重变化，耕作层逐渐变浅，犁底层变厚。耕作层变浅导致农作物在生长中后期根系不能向纵深方向生长，很容易出现倒伏，同时耕地不耐涝，不抗旱。传统农业生产模式下，耕地土壤中腐熟质含量逐年下降，耕地后劲严重不足。而通过积极应用机械化深松技术可以疏松深层土壤，打破犁底层，同时还不会破坏土壤结构和地表植被，提高土壤蓄水能力。

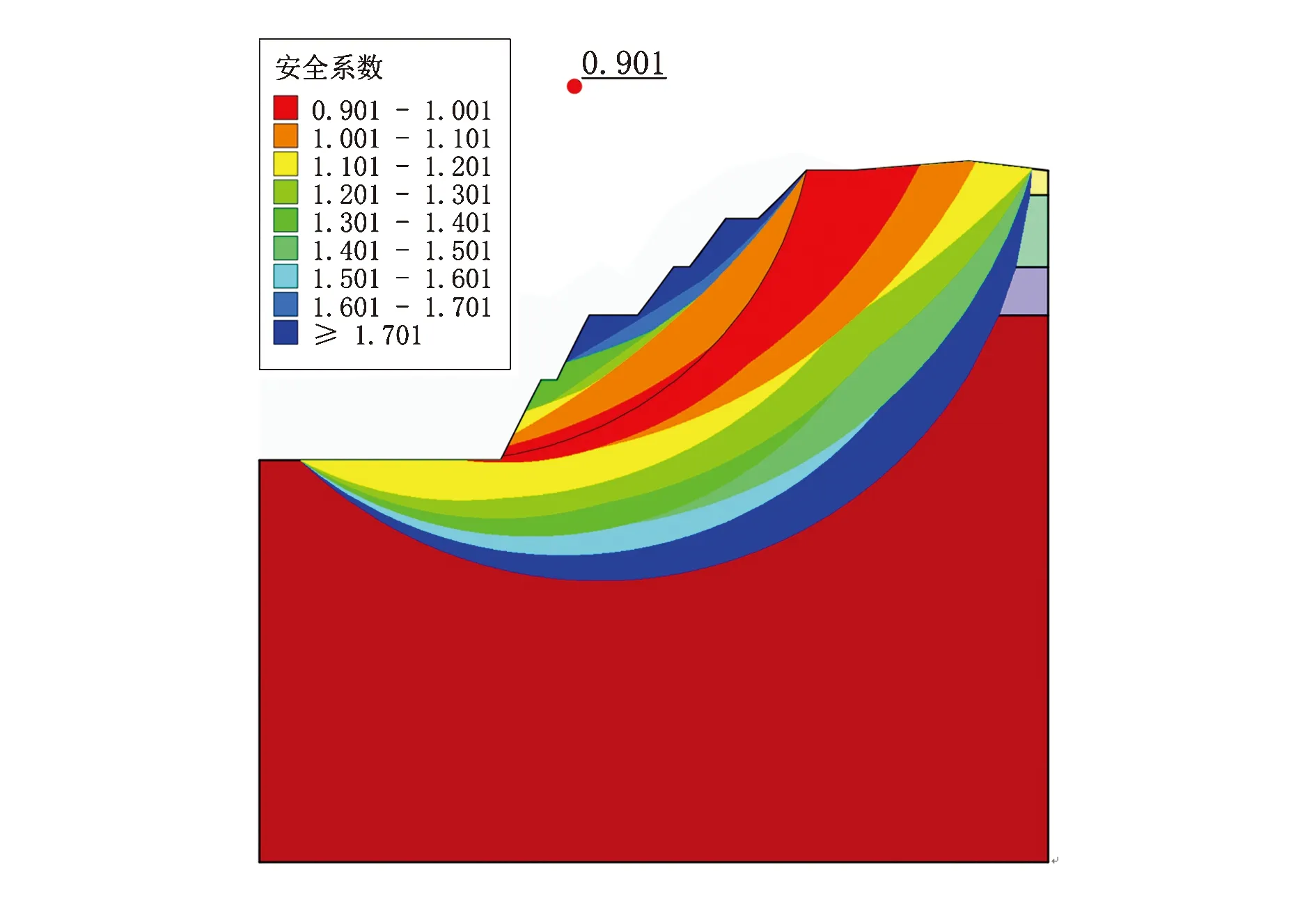
图4 工况2边坡安全系数云图Fig.4 Safety factor nephogram of slope under working condition two

图5为两种强度指标下最小安全系数随边坡开挖深度的变化图，可以看到，在对边坡进行开挖的过程中，受地形影响最小安全系数略有增大的迹象，但随着卸荷作用增强，边坡稳定性开始降低，由于在实际的削坡过程中，在卸荷作用下，边坡底部的岩体会产生应力释放现象使得岩体质量级别降低，从而使边坡稳定性也随之进一步降低，因此当边坡开挖至砂岩层时，两种强度指标下的边坡安全系数差异逐渐明显，随卸荷深度的增大，岩体强度由峰值向残余值过度，滑移面上的剪力将开始由衰减后的残余黏聚力与残余摩擦角承担，此时采用残余强度计算的边坡安全系数降低速率明显增大，最终导致该边坡破坏，而采用峰值强度的边坡由于其没有充分考虑卸荷作用对边坡岩体造成的损伤，因此该状态下的边坡依然处于稳定状态，从而背离边坡的实际工况.两种不同强度指标最终计算结果显示，采用残余强度的边坡最小安全系数较峰值强度计算结果减小28%，砂岩强度衰减对边坡稳定性影响明显.

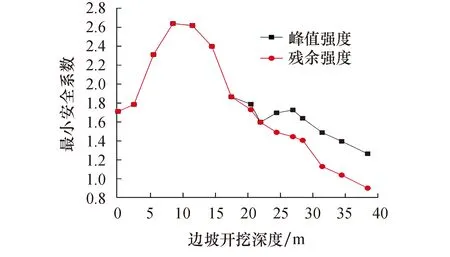
图5 边坡最小安全系数与开挖深度关系

3.2 边坡变形特征分析

一般情况下，边坡的位移变化可以更直观地反应其稳定性变化的规律，因此进一步对两种强度指标下的边坡位移有限元计算结果进行分析，所得边坡位移云图如图6、图7所示.

通过图6、图7中位移矢量箭头的指向可以看到在强烈的卸荷作用下，两种不同强度状态下的边坡均发生剧烈的回弹变形，竖直向上方向的位移分量在边坡变形中占主导地位，只有在顶部垂直卸荷作用较小的部位，指向坡体临空侧的水平位移才成为位移矢量构成中的主要部分，因此该边坡在实际发生失稳时产生的裂缝多为剪出破坏裂缝.此外，对边坡位移场的进一步分析可以看到，卸荷回弹产生的变形较大值集中分布于边坡浅层表面，并有向边坡坡体内部方向逐渐衰减，向边坡坡脚及坡脚前缘方向逐步增强的趋势.在此基础上进一步分析对比两种不同强度下的边坡总位移.由于在该边坡的开挖过程中，卸荷作用会降低围压，破坏岩体原有的应力平衡状态，促使边坡岩体产生变形和破裂，此时边坡底部砂岩强度指标衰减为残余值，边坡整体抵抗变形的能力降低，因此在图7的图例中表现为以残余强度为基础计算的开挖后的位移水平总体高于峰值强度下的边坡.此外，由于岩体碎裂导致的边坡底部变形将进一步地影响岩层上覆土体的变形，因此如图7所示，坡体中下部有滑动趋势的区域将进一步向坡体上部延伸，最终与坡顶有滑动趋势的区域联通后使坡体发生破坏，这与边坡实际所产生的砂岩层压溃黄土层整体滑塌的破坏形式基本一致.

图6 工况1位移矢量云图Fig.6 Displacement nephogram of working condition one

综上所述，该深挖路堑边坡的破坏过程可以描述为：坡体的卸荷作用使得边坡发生较强的回弹变形，该变形进一步发展使底部岩体碎裂，坡底岩层强度衰减至残余值，进而在底部软弱面上产生滑移趋势，且在削坡过程中滑移趋势进一步发展，并与上覆土层的不稳定区域联通形成滑移面，滑移面底部岩体在蠕滑过程中被上覆土层压溃，而上覆土层也因失去底部岩体支撑加速下滑,最终发生大范围的坡体破坏.所以此类边坡稳定性受底部岩体力学性质影响较大.为进一步探究两种岩体强度下的坡体深层位移变化规律，按图8所示对边坡H1系进行测点布置.取部分关键施工过程进行模拟得到两种不同强度下坡体内部深层总位移变化情况，如图9所示.

图8 测点布置图Fig.8 Arrangement of measure-point

由图9可以看出，两种不同强度下的边坡位移值均对边坡卸荷作用变化敏感，在初期开挖过程中由于卸荷区域较为接近边坡顶层中部，因此测点曲线在50～60 m的区域内位移值较大，而在该区域两边的位移值则相对较小.随着开挖逐渐接近坡脚位置，边坡的卸荷作用引起坡脚浅层区域剧烈的回弹变形，此时的变形大体上遵循了沿边坡内部方向逐渐减小的规律.进一步分析边坡在削坡过程中的位移增量变化可以看到，各测点所测得的总位移增量呈先增大后减小的趋势，这是因为初期的卸荷作用使顶部土体对岩体的变形约束能力降低，卸荷土层下方的岩体开始产生回弹变形.随着卸荷作用的增强，坡体表面出现更加剧烈的卸荷回弹，坡体位移随之增大.当边坡开挖接近坡底时，此时的岩层上方卸荷量逐渐减小，因此测点处整体位移增量也随之减小.

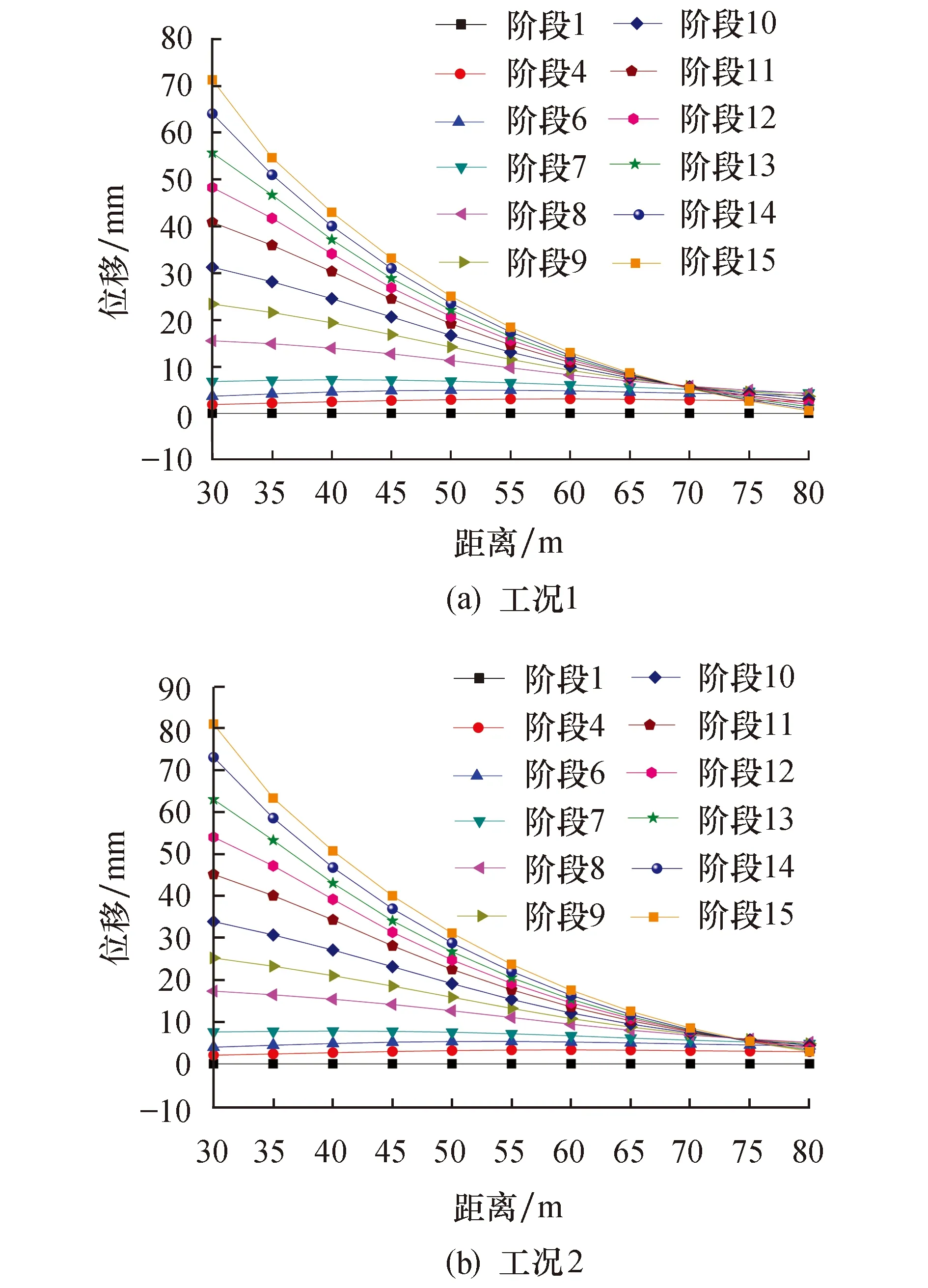
图9 坡内H1系位移变化规律

对图9a的进一步分析可以看出，在距离边坡坡脚40～50 m处的测点测得的总位移值在坡体开挖后期减小现象明显，至最后一步开挖时，部分测点所测得结果表现出一定的下滑趋势，这是因为削坡过程中剧烈的不均匀变形使岩层中的部分岩体抗剪强度达到极限值并产生破坏，其承担的荷载将由周围的岩体继续承载，在荷载传递过程中，周围的岩体也随之发生强度衰减或者破坏， 最终将形成一条贯穿坡体的有滑动趋势的滑带，滑带内的岩土体将沿滑面产生曲线滑动的趋势，从而使得靠近该滑面上的测点出现位移减小的现象.若将图9a中70 m处定义为该边坡的滑移面参考边界点，通过将其与图9b的模拟结果对比可以直观地发现，以残余强度计算的边坡其参考边界点距离坡角更远，这意味着该强度下处于不稳定状态的坡体范围更大，此判断与前文中以边坡安全系数云图为基础所做出的分析一致.此外，增大的不稳定坡体将引起更为剧烈的破坏，因此选取一种合理的加固方式对边坡进行有效支护就成为了当务之急.

4 预应力锚杆加固效果分析

4.1 预应力锚杆锚固机制

预应力锚杆作为一种主动支护技术，在边坡工程中得到了大量的应用.其加固原理可概括为：由于预应力的使用，使锚固地层产生压应力区并对加固地层起加筋作用；可以增强地层的强度，改善地层的力学性能：可以使结构与地层连接在一起，形成一种共同工作的复合体，使其能有效地承受拉力和剪力，并能提高潜在滑移面上的抗剪强度，有效地阻止坡体滑移[19].在深挖路堑边坡工程中，坡底软岩往往在卸荷作用引起的应力释放过程中发生破裂致使岩体强度参数衰减，而预应力锚杆则通过对岩土体施加压应力场将破碎的岩体缝缀在一起，改善了锚杆加固区的岩体力学参数，强化了边坡底部岩体破裂后的强度，从而达到保持边坡稳定的目的.为进一步探讨预应力锚杆对深挖路堑边坡的加固效果，本文假定该二元结构边坡在开挖过程中沿砂岩层自上而下共设置五道锚杆，每道锚杆与水平面的夹角为15°，第一、三道锚杆坡顶埋深均为2 m，锚杆竖向间距均为3 m，其余锚杆计算参数见表2，并根据前文总结，采用岩体强度衰减后的残余强度对预应力锚杆加固边坡的效果进行分析.锚杆支护边坡有限元模型图如图10所示.

表2 锚杆设计参数Tab.2 Designed parameters of structure

图10 锚索支护边坡数值模型图Fig.10 Numerical model of slope supported by anchor

4.2 边坡变形对比分析

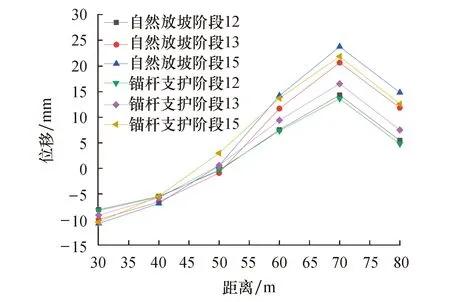
图11 边坡水平位移对比Fig.11 Comparison of horizontal displacement of slope

图12、图13分别为坡内H2系测点测得的预应力锚杆支护前后坡体内部x方向应变及剪应变对比图.通过图12、图13可以看到边坡在开挖过程中施加锚杆支护后，坡体深部应变场发生了一定的变化.由图12可知，边坡开挖过程中坡体正应变会逐步增大，但相对于无支护边坡，带支护边坡由于锚杆轴向预应力场提高了坡内压应力水平，因此支护后的坡体深部x方向应变水平始终保持较高的数值，且支护后边坡受应力扩散影响，x方向的应变沿锚杆长度方向由坡面向坡内逐步减小，说明锚杆预应力确实参与了控制边坡变形的工作.由图13可知边坡在支护后，加固后的边坡剪应变水平有所减小，在锚杆预压应力场作用下，卸荷作用造成的临空面围压损失得到补偿，且在围压作用下，岩体原本减弱的抗剪强度进一步提升，从而使坡体剪应变水平降低.对比图12、图13可以看到坡体剪应变水平数值始终高出正应变水平数值一个量级，这表明此类深挖路堑边坡在施工的动态变化过程中，造成其变形的主要原因依然是岩土体强度衰减导致的剪切变形.

图12 边坡x方向应变对比Fig.12 Comparison of positive strain of slope

图13 边坡剪应变对比

4.3 边坡稳定性对比分析

图14、图15分别为支护前后的剪应力云图，可以看到削坡过程结束后将在砂岩层坡脚处发生应力集中现象，坡体内的剪应力由坡脚处向周边土体扩散衰减，坡体内剪应力的较大值基本集中于砂岩层，一旦砂岩层因抗剪强度达到极限值出现破坏势必将引起边坡发生牵引式破坏，由此可见砂岩层的稳定性对边坡整体稳定性有着至关重要的作用.在对边坡砂岩层采用预应力锚杆加固后，坡体上覆土层的剪应力值分布变化程度较小，但在锚杆与土体之间相互作用的扰动下，边坡内部剪应力场在锚杆锚固段周围发生明显的扭曲，而锚杆的预应力场与坡体卸荷后的应力场相互叠加也使砂岩层坡面下部部分区域的剪应力场分布形式发生改变，坡脚处应力集中现象得到改善.

图14 支护前边坡剪应力云图Fig.14 Shear stress nephogram of the slope without anchor

图15 支护后边坡剪应力云图

进一步从边坡安全系数角度分析锚杆加固对边坡稳定性影响.由图16可以看到在卸荷过程中，由于锚杆对土体施加的压应力场改善了因开挖卸荷而导致强度衰减的底部岩体的力学性质，增强了破裂岩体之间的相互作用，因此随着锚杆的介入，边坡在开挖过程中的稳定性趋于恒定，且在进一步的卸荷过程中，因预应力锚杆数目增多，边坡安全系数有所增长，最终安全系数将维持在1.5以上.反之，在自然放坡的条件下，当削坡至坡底砂岩层时，由于开挖卸荷造成的岩体损伤得不到有效控制，岩层内的塑性区进一步发展，坡体稳定性加速下降，最终随着坡底至坡顶的塑性区贯通，边坡发生失稳破坏.

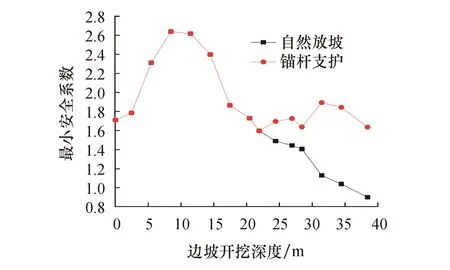
图16 边坡安全系数变化对比Fig.16 Comparison of minimum safety factor

综上分析可以看到黄土-砂岩二元结构边坡的稳定性与底层基岩强度关系紧密，若该边坡在施工阶段能及时采用预应力锚杆对底层软岩进行加固将能避免此类滑塌的发生.

5 结论

通过在对兰永线K35+000～150标段黄土-砂岩二元结构高边坡失稳破坏机制分析的基础上采用峰值强度和残余强度对边坡进行模拟结果的对比分析，得出如下结论：

1) 在深挖路堑施工过程中，砂岩受卸荷作用产生应力释放现象，该现象将驱使砂岩破裂从而使砂岩层整体强度发生衰减进而影响边坡的稳定性.以残余强度为基础对边坡稳定性分析可更贴近边坡实际状态，若以峰值强度计算和分析此类边坡，所得的结论可能偏于危险.

2) 深挖路堑边坡会在削坡过程中产生剧烈的卸荷回弹，其中竖直方向的回弹变形占主导地位，而此类边坡的水平位移则主要集中于边坡卸荷作用较弱的坡顶局部区域.

3) 深挖路堑边坡支护前后坡内的剪应变水平均保持较高的数值，但预应力锚杆通过对边坡施加压应力场将补偿坡体在开挖过程中的围压损失，在约束边坡向临空侧变形的同时提高边坡岩土体的抗剪强度，从而在一定程度上降低边坡的剪应变水平.

4) 深挖路堑边坡剪应力分布规律与剪应变分布规律类似，均表现出由各级边坡坡面向边坡深部方向逐步减小的趋势，其中边坡坡体剪应力的较大值基本集中于砂岩层，因此砂岩层的应力状态对边坡稳定性有较大的影响.

5) 采用预应力锚杆加固二元结构边坡底层基岩可以改变坡体内部应力分布形式，其产生的压应力场可以增强破裂岩体间的相互作用，改善岩体力学性质，从而有效提高残余强度下的边坡稳定性，进而避免边坡破坏的发生.