面向能量天平同步测量的磁链差测量方法研究

钱璐帅, 李正坤, 白 洋, 许金鑫, 赵 伟, 张钟华

(1. 清华大学 电机工程与应用电子技术系, 北京 100084；2. 中国计量科学研究院, 北京 100029； 3. 国家市场监管总局电学量子重点实验室, 北京 100029；4. 中国计量大学, 浙江 杭州 310018)

1 引 言

质量单位千克是国际单位制中7个基本单位之一,于2019年5月20日启用了基于普朗克常数的量子化新定义[1, 2]。此后,千克将通过硅球法[3, 4]、功率天平法[5]、能量天平法[6]等进行复现和量传。其中,能量天平法是张钟华等提出的千克量子化定义复现方法,其由2个测量模式组成,分别为：称重模式和磁链差测量模式[7]。按传统方法实施测量时,上述2个测量模式是交替执行的,因此悬挂线圈在不同测量模式下所交链的磁通量差异,将引入测量不确定度[8]。针对上述问题,本文作者提出了一种能量天平同步测量方法[9],具体是将原分时测量的称重模式和磁链差测量模式合二为一,以保证悬挂线圈在不同测量模式下所交链的磁通量完全一致,从而抑制上述提及的测量不确定度影响。与传统测量方法相比,单次磁链差测量在同步测量过程中消耗的时间会显著增长。磁链差测量的核心,是对线圈感应电压的时间积分进行测量。原有的磁链差测量方法是基于数字积分原理的,具体是利用美国NI公司生产的PXI-5922型数据采集卡测得瞬时感应电压,然后乘以积分时间,以得到近似的磁链差值[10]。研究发现,PXI-5922的核心工作器件是Σ-Δ型模数转换器(analog to digital converter, ADC),其应用于磁链差测量时存在如下2方面问题：

1)Σ-Δ型ADC的电平保持采样过程和数字量化过程,共同导致一个与采样频率呈反比的磁链差测量偏差；

2)PXI-5922内部电路中存在的时变噪声,引入与积分时长正相关的磁链差测量不确定度。

受上述2方面问题制约,原磁链差测量方法在同步测量过程中无法实现10-8量级的相对标准不确定度。因此,本文利用双积分型ADC的模拟积分测量特性,提出了一种无测量死区,并且支持时变噪声分时清零的磁链差测量方法。在此基础上,本文将详细评估改进后的磁链差测量系统的相对标准不确定度。

2 磁链差测量原理及原方法的局限性

根据法拉第电磁感应定律,当能量天平中的磁体系统沿竖直方向相对于静止的悬挂线圈运动时,悬挂线圈中将产生感应电压。在同步测量过程中,磁体系统在40 mm的垂向运动区间内,被锁定在6个不同位置,配合悬挂线圈进行称重测量。因此,磁体运动包含5次加速、匀速以及减速过程,与之对应的感应电压波形示意图如图1所示。其中,磁体匀速运动过程对应的感应电压幅值约为1.1 V。

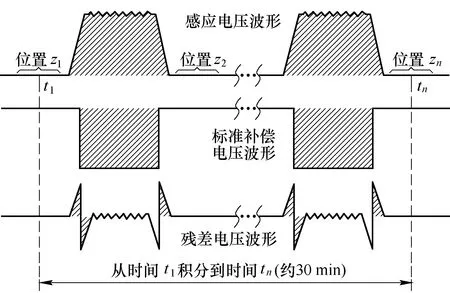
图1 磁链差测量基本原理示意图Fig.1 The basic principle of flux linkage difference measurement

在磁链差测量过程中,若伏特量级的感应电压直接送入电压采集设备,则测量结果将受到电压采集设备自身零位偏置和增益误差的影响,难以实现高准确度测量[10]。为此,能量天平中采用了如下2种误差抑制措施：

第一,为抑制零位偏置的影响,采用磁体换向运动方式进行磁链差测量。具体地,磁体系统首先由相对位置z1运动至位置zn,对应测得磁链差值 [ψ(zn)-ψ(z1)]；随后,令磁体反向运动,则测得磁链差值[ψ(z1)-ψ(zn)]。取上述两次测量结果的差值,便可以抑制零位偏置的影响。

第二,为抑制增益误差的影响,事先利用可编程约瑟夫森量子电压标准系统(programmable Josephson voltage standard,PJVS)对电压采集设备的增益系数进行校准[11]。如此,感应电压测量过程中,便可根据校准结果对测得数据进行比例修正。然而,受电子元件稳定性影响,电压采集设备的增益系数会缓慢变化。由于能量天平需要连续运行多日,因此增益系数缓变有可能引入10-8量级及以上的磁链差测量相对标准不确定度,具体影响程度与所使用的电压采集设备有关。针对该问题,可利用PJVS系统产生图1所示的标准电压波形,用以对感应电压波形进行补偿[10]。随即,电压采集设备便更改为测量两者的残差。虽然残差电压测量结果仍将受到增益系数波动的影响,但该条件下的测量误差相对于原被测感应电压已属于小量。因此,由增益误差引入的磁链差测量相对标准不确定度便可以优化至少1个数量级。

之前实现磁链差测量时,是选用PXI-5922型数据采集卡作为残差电压测量设备,其中的核心器件是Σ-Δ型ADC。Σ-Δ型ADC工作时,需要电平保持电路参与,以保证其模数转换过程中被转换的电平恒定不变[12]。因此,基于Σ-Δ型ADC的磁链差测量方法是以数字积分原理为基础的,其具体机理如图2所示。在图2中,单实线曲线表示被采样的残差电压波形；粗圆点代表实际采样点；斜线阴影区域表征模数转换阶段,在该阶段中电平持续保持不变；反斜线阴影区域则为数据量化阶段,由于该阶段停止电压采样并准备输出数据,因此被称为测量死区。按照图2所示的测量方法,是以实际采样点的瞬时电压值作为整个采样周期dt内的平均电压值进行输出。如此,即以图2中矩形框包围的面积替代了真实残差电压曲线包围的面积。当采样频率设定未能满足采样定律,又或者是残差电压信号中所有的频率分量未能被整周期地采样时,基于上述方法测得的磁链差值将偏离其真值。在保证同等采样分辨率及采样准确性前提下,采样频率越高,上述偏差越小。

图2 基于Σ-Δ型ADC的磁链差测量机理Fig.2 Flux linkage difference measurement mechanism based on the Σ-Δ type ADC

因上述保持采样过程与测量死区引入的磁链差测量相对标准不确定度,可以采用如下实验方法进行评估。首先,在同步测量过程中屏蔽称重测量功能,以提高磁链差测量效率；然后,依次提取PXI-5922测得的残差电压波形中相邻2个采样点之间的电压差值。将所有差值累加求和后,乘以采样周期的二分之一。如此,便近似得到了图2中残差电压曲线包围面积和矩形框包围面积之间的差值。取所述面积差重复测量的平均值,除以主磁链差值,便得到了磁链差测量相对标准不确定度的估计值。实验结果表明,当PXI-5922的采样频率大于10 kHz时,上述磁链差测量相对标准不确定度可以达到10-9量级。然而,较高的采样频率意味着需要大容量的原始数据存储空间,同时也为数据处理系统带来较大负担,这在实施同步测量时的表现尤为显著。

综上所述,原磁链差测量方法无法满足10-8量级的同步测量准确性需求。

3 基于双积分型ADC的磁链差测量方法

在电测技术领域,ADC是构建电压积分测量系统的核心器件。根据工作原理不同,目前已成熟应用的ADC可分类为：逐次逼近型、双积分型、并行比较型、压频变换型、Σ-Δ型以及流水线性等[14]。其中,双积分型ADC采样时不存在电平保持过程,而是直接对被采样的电压信号进行模拟积分测量,这与磁链差测量的需求高度吻合。因此,本文基于双积分型ADC展开磁链差测量方法研究。

双积分型ADC的工作过程,区分为定时积分与定值积分2个阶段。在这2个阶段中,ADC内部的积分器分别对待测的电压信号和ADC内部的参考电压信号进行积分。通过将固定积分时间内被测电压信号的平均值转换为与之成正比的时间间隔,结合时钟脉冲与计数器完成对所述电压平均值的数字量化。如此,基于单一双积分型ADC的磁链差测量机理如图3所示。在图3中,单实线曲线代表被采样的残差电压波形；斜线阴影区域表示定时积分阶段,相应的加粗线段代表实际被积分的波形；水平线阴影区域代表定值积分阶段；而反斜线阴影区域则对应于数据量化阶段。在定值积分和数据量化阶段,ADC并未对残差电压波形进行积分,因此均视为测量死区。按照图3所示的测量方法,是以定时积分阶段的平均电压值作为采样周期dt内的平均电压值进行输出。相应地,就是以阴影区域面积替代了残差电压曲线包围的面积。因此,基于单一双积分型ADC测得的磁链差值中,同样包含了由测量死区引入的测量不确定度。

图3 基于单一双积分型ADC的磁链差测量机理Fig.3 Flux linkage difference measurement mechanism with the single dual-slop integration based ADC

总结PXI-5922的应用经验,测量死区的影响可以通过增大采样频率的方式加以抑制。再者,为了减轻数据处理与存储系统的负担,本文提出了一种基于并联ADC接续触发的电压分时采样方法。如图4所示,优化的残差电压测量单元由多个支持外部触发的双积分型ADC组成,它们的输入端并联后,共同连接被采样的残差电压信号。磁链差测量初始,ADC_1在外部触发信号的作用下开始定时积分,此时,其余ADC均处于待机状态；待ADC_1定时积分完毕,其立即输出触发脉冲至ADC_2,则ADC_2开始定时积分,此时,ADC_1处于定值积分与数据量化阶段。若ADC_2定时积分结束前,能够确保ADC_1已处于待机状态；那么,ADC_2在定时积分完毕时,将立即输出触发脉冲至ADC_1,则ADC_1再次开始定时积分。如此反复,能够保证待采样的残差电压波形都能被ADC积分。若ADC_2定时积分结束时,ADC_1仍处于定值积分或数据量化阶段,则ADC_2输出的脉冲将触发ADC_3开始测量,以便为ADC_1留出足够的时间完成其首次积分测量。这样,ADC_1、ADC_2和ADC_3便构成了一个闭合测量环,从而能够消除测量死区。待测量结束时,累加所有ADC的测量结果,并与设定的定时积分时间相乘,便可得到所需的磁链差值。

上述测量方法,可以消除由测量死区引入的磁链差测量不确定度；然而,由设备时变噪声引入的不确定度分量还未被消除。针对这一问题,本文在分时采样的基础上提出了一种时变噪声分时清零方法。如图4所示,在某一ADC完成数据量化工作后,其并未进入待机状态,而是主动断开其与被采样信号的电气连接,并短路其信号输入端。紧接着,该ADC便对一个定时积分周期内的平均噪声幅值进行测量。待测量完毕,便从之前的残差电压测量结果中减去这一平均噪声幅值。该方法虽然未能直接剔除残差电压信号测量时刻的时变噪声,但是只要相邻2个采样周期内的时变噪声并非急剧变化,则该方法仍然有助于减小时变噪声累积的影响。实现上述时变噪声清零功能,需要消耗额外的采样时间,其影响等效于前述存在的测量死区。但由前文分析可知,附加测量死区的影响可以通过并联适当数量的ADC加以消除。

图4 基于并联双积分型ADC接续触发的磁链差测量机理Fig.4 Flux linkage difference measurement mechanism with multiple alternately triggered dual-slop integration based ADC

在新方法中,残差电压测量单元的整体采样频率,可通过调整ADC的定时积分时间进行控制。由于测量死区的影响已经被消除,因此整体采样频率可以设置在Hz量级。如此,就可以大幅度减小原始数据存储空间。

4 磁链差测量系统不确定度评定

为了验证本文提出的磁链差测量方法的有效性,需要基于双积分型ADC搭建残差电压测量单元。分析发现,Agilent-3458A型数字多用表的直流电压测量功能,正是基于双积分型ADC原理工作的,并且具备外部触发使能测量、定时积分完毕输出触发脉冲、仪表噪声清零等功能。因此,Agilent-3458A满足重构残差电压测量单元的基本条件。由Agilent-3458A的测量时序可知,需要3台Agilent-3458A进行接续测量,如此才能在实现时变噪声清零功能的基础上,消除测量死区的影响。基于上述分析,改进后的磁链差测量系统如图5所示。其中,悬挂线圈中的感应电压与PJVS系统产生的标准电压,经由一台低热电势扫描开关串接,从而实现电压补偿,并利用现场可编程门阵列(field programmable gate array,FPGA)输出定时触发脉冲,以保证2个电压信号之间的时间同步。重构的残差电压测量单元由3台Agilent-3458A并联组成。为保证测量系统中不同设备的时间/频率一致性,利用FS725型铷原子钟提供10 MHz频率基准,其相对标准不确定度处于10-11量级。FPGA和Agilent-3458A所需的特殊时基,由4台Agilent-33250A任意波形发生器转换得到。

图5 改进后的磁链差测量系统示意图Fig.5 Schematic diagram of the improved flux linkage difference measurement system

如第3节所述,理论上只需要将图5所示系统中的3台Agilent-3458A配置为循环触发形式,便可以消除测量死区的影响。但Agilent-3458A的触发特性并非完全理想,体现在：(1)Agilent-3458A定时积分完毕输出的下降边沿,其下降时间约为50 ns；(2)Agilent-3458A采用低电平阈值为0.4 V的TTL电平逻辑来识别外部输入的下降边沿,因此前一台Agilent-3458A输出的下降边沿需要经过约45 ns的延时才能被后一台Agilent-3458A所识别；(3)Agilent-3458A在识别外部输入的下降边沿后,需要经过一段固定延时才能开始积分测量,并且,待定时积分测量完毕,同样需要经过一段固定延时才能输出触发脉冲,经测量,这两部分固定延时的总和约为650 ns。综上,相邻2次定时积分测量之间共存在约700 ns的测量死区。在与Agilent公司的技术人员交流后得知,该测量死区无法通过参数配置方式进行调整。因此,需要评估其在磁链差测量过程中引入的相对标准不确定度。

一种可行的减小所述测量死区的方法,是利用FPGA产生精确定时的触发脉冲,并按照既定顺序依次触发3台Agilent-3458A进行测量。虽然3台Agilent-3458A均经过固定的延时方能开始积分测量,但是相邻2台Agilent-3458A之间的测量死区,只取决于它们各自固定延时之间的差值。经测量,所述的固定延时差值不超过40 ns。因此,由测量死区引入的磁链差测量相对标准不确定度优化至 3.3×10-9。综上所述,虽然本文提出的电压分时采样方法理论上能够完全消除测量死区的影响,但受所用测量仪器自身触发特性的限制,测量死区仍将继续存在于改进后的磁链差测量系统中,并因此引入10-9量级的相对标准不确定度。

由Agilent-3458A内部时变噪声引入的磁链差测量相对标准不确定度,采用第2节中的磁链差模拟测量实验进行评估。实验过程中,图5所示系统中的3台Agilent-3458A的信号输入端被短路,FPGA同步输出3路周期为3 s的触发脉冲至3台Agilent-3458A,相邻两路触发脉冲之间的时间间隔以及Agilent-3458A单次采样的定时积分时间均设定为1 s,即表明残差电压测量单元的综合采样频率为1 Hz。在应用本文提出的时变噪声分时清零方法的条件下,实验测得的20个磁链差模拟测量结果如图6中的红色圆点所示(对应于左侧垂向坐标轴)。经统计,所有数据的均值标准偏差约为7.5×10-7V·s。相对于46.0 V·s的主磁链差值而言,则时变噪声累积引入的磁链差测量相对标准不确定度约为1.6×10-8。若关闭时变噪声分时清零功能,则同等条件下测得的磁链差模拟测量结果如图6中的蓝色方块所示(对应于右侧垂向坐标轴)。经统计,该条件下因时变噪声累积引入的磁链差测量相对标准不确定度劣化至3.6×10-6。由此可见,本文提出的时变噪声分时清零方法是有效的。

图6 磁链差模拟测量结果Fig.6 Results of flux linkage difference simulation measurement

在磁链差测量的数据处理阶段,是默认PJVS系统输出的补偿电压波形为标准矩形波,并以此来计算其包围的补偿面积的。而事实上,受PJVS系统泄漏阻抗和量子电压暂态特性这两方面因素的影响[15],实际的补偿面积会偏离其理论值。一方面,利用导线引出量子电压的过程中,由于正、负电极的输出引线之间,以及输出引线与大地之间的泄漏阻抗并非无穷大,因而不可避免地存在泄漏电流。如此,实际接入到磁链差测量系统中的补偿电压,将在引线电阻的分压作用下偏离其量子值。前期,本文作者所在课题组已经对能量天平中PJVS系统的泄漏阻抗进行过测量,评估认为其将在磁链差测量中引入约1.2×10-9的相对标准不确定度[16]。另一方面,量子电压芯片属于电流控制型器件。由于PJVS系统需要一定时间来建立稳定的偏置电流输出,因此量子电压变换存在暂态过程。经测试,当PJVS系统输出±1.135 V的标准电压时,其上升和下降边沿的持续时间分别为2.5 μs和1.3 μs。当输出的量子电压的正负号改变时,升降边沿的形状和持续时间均未发生明显变化。测试结果表明,同步测量过程中由5次量子电压暂态过程导致的补偿面积偏差约为1.26×10-6V·s,其相对于46.0 V·s的主磁链差值的相对偏差约为2.7×10-8。考虑到量子电压暂态过程导致的补偿面积差值十分稳定,因此,可以利用测得的补偿面积差值对理论计算值加以修正,并取补偿面积差值重复测量的相对均值标准偏差作为修正不确定度的评定依据,具体约为2.5×10-9。

由磁链差测量原理可知,磁链差测量结果还与积分时间的准确性有关,具体表现为Agilent-3458A定时积分时间的准确性,以及FPGA定时触发脉冲间隔的准确性。利用SR620型时间间隔/频率计数器测量Agilent-3458A和FPGA的输出脉冲发现,两者的定时准确性均优于2.0×10-9,短期稳定性均优于1.0×10-9。测量过程中,SR620的外部时钟参考已锁定至10 MHz铷原子钟。因此,由积分时间误差引入的磁链差测量相对标准不确定度小于 2.0×10-9。

将上述所有的磁链差测量不确定度分量列于表1中。根据合成不确定度评定原则,可以计算得到磁链差测量的相对标准不确定度约为1.7×10-8。因此,本文提出的基于双积分型ADC的磁链差测量方法,可以满足能量天平同步测量过程实现5×10-8的相对标准不确定度的测量需求。

表1 磁链差测量不确定度评估表Tab.1 Uncertainty evaluation form of flux linkage difference measurement ×10-9

5 结 论

本文提出的一种基于并联双积分型ADC分时采样和分时清零的磁链差测量方法,解决了原能量天平磁链差测量系统中,测量死区与时变噪声引入过大测量不确定度的问题。该方法利用双积分型ADC直接积分模拟电压而无保持采样的特点,结合多ADC并联方式实现分时接续测量,有效抑制了测量死区的影响。利用并联ADC分时清零方法,避免时变噪声在积分测量中逐步累积,有效抑制了时变噪声的影响。实验结果表明,上述新方法可将同步测量过程中的磁链差测量相对标准不确定度由原来的10-6量级抑制至1.7×10-8,为能量天平实现不确定度优于5×10-8的测量能力以及建立我国自主研发的质量量子化基准装置提供了重要的技术支撑。