基于粒子群算法和支持向量机的大学英语教学效果评价模型

张菊玲

(西安思源学院 文商学院， 陕西 西安 710061)

0 引言

现阶段，对大学英语教学效果评价是高校教育评价的重要研究问题。教师根据评价结果，实时了解教学效果，及时调整教学方案与进度[1-3]。学校领导层通过评价结果对英语老师综合教学水平实施评价[4]，科学合理的评价模型使评价对象变得更加优秀。相关资料显示，在大学英语教学效果评价中存在许多问题[5]。比如原有评价方式过于依靠评价者的经验。评价主体的主观因素影响评价结果公平。因此在大学英语教学效果评价中，急需定量化的评价方法。

但是以往大学英语教学效果评价方法非常局限，如范岩等[6]研究优化BP神经网络的高校教学质量评价模型，在大学英语教学效果评价过程中，由于该方法忽略了影响教学质量的因素，导致大学英语教学效果评价精度不佳；王红艳等[7]研究基于类别加权灰靶决策的教学评价的方法，在大学英语教学效果评价中，由于该方法计算过程复杂导致大学英语教学效果评价效率低。

粒子群算法是对随机粒子群体，利用个体间信息共享与传递实施全局搜索[8-9]。为了更新下一代迭代的位置及速度，在迭代内，各粒子在种群内搜索全局极值与个体极值。最小二乘支持向量机是支持向量机的拓展，简化了支持向量机的求解过程，其待选参数少[10]。

因此本文研究基于粒子群算法和支持向量机的大学英语教学效果评价模型方法。该方法避免主观思维和随机因素的影响，科学合理地对大学英语教学效果进行评价[11]。

1 基于粒子群算法和支持向量机的大学英语教学效果评价模型

1.1 构建大学英语教学效果评价体系

针对大学英语教学效果评价体系有多种理论。依据相关理论构建以教师和学生为主体的多指标体系。大学英语教学效果评价指标体系，如图1所示。

图1中，大学英语教学效果评价指标体系包括来自学生的英语教学评价指标与英语教师教学评价指标。其中，教师责任心、英语成绩是大学英语教学效果重要的评价指标。将大学英语教学效果评价指标数据作为最小二乘支持向量机的输入样本，实现大学英语教学效果评价。

1.2 最小二乘支持向量机评价原理

最小二乘支持向量机评价原理：设定1组训练样本集用s={xi,yi}描述，其中i=1,2,…,l。最小二乘支持向量机的输入数据用xi描述；训练样本个数用l描述；输出数据用yi描述。在d维空间里的线性回归函数为式(1)。

y=ωTx+b

(1)

其中，偏差量用b描述；权向量用ω描述。

在高维特征空间里的回归函数为式(2)。

f(x)=ωTφ(x)+b

(2)

其中，φ(x)为输入空间到高维特征空间的非线性映射。

最小二乘支持向量机的优化目标函数为式(3)。

(3)

约束条件为式(4)。

s.t.ωTφ(xi)+b+ei=yi,i=1,2,…,l

(4)

其中，c为正则化参数控制表示对误差的惩罚程度；ei为误差变量。

采用引入Lagrange乘子，使约束优化转变为无约束优化问题，实现优化问题的求解，即式(5)。

(5)

其中，Lagrange乘子用λ描述。

最优值的计算是在KKT优化条件下得出。最优值求解为式(6)。

(6)

将式(6)里的ω和e消除，二次优化问题换为求解线性方程组计算问题，计算结果，即式(7)。

(7)

其中，λ=[λ1，λ2，…，λl]T;Q=[1，1，…，1]T;I表示单位矩阵；Ω∈Rl×l,且Ωij=φ(xi)Tφ(xj)=K(xi,xj);K(·)表示函数。用原空间内的核函数，获取最小二乘支持向量机的回归函数，为式(8)。

(8)

为了规避维数灾难的发生[12]，引入最小二乘支持向量机常用的有径向基核函数，代替高维特征空间的内积运算。径向基核函数为式(9)。

(9)

其中，核函数参数宽度为σ。

优化c和σ表示2个参数，增强最小二乘支持向量机的泛化能力。最小二乘支持向量机参数寻优问题采用粒子群算法。最小二乘支持向量机实施大学英语教学效果评价模型的流程如下。

Step 1：输入大学英语教学效果评价数据的样本。

Step 2：最优核函数参数σ与正则化参数c求解，采用粒子群算法实施搜索。

Step 3：选取合适的核函数。

Step 4：计算获取最优化问题，计算出最优解用α描述，如式(10)。

(10)

Step 5：决策函数的构建，构建过程，如式(11)。

(11)

Step 6：通过决策函数实施模型评价。

1.3 粒子群算法搜索最小二乘支持向量机参数

设定由m个粒子构成1个种群，在1个d维的搜索空间里，其中第i个粒子在d维空间内搜索到的最优位置用pi描述；速度用vi描述；第i个粒子在d维空间内的位置用xi描述；定义向量用xi=(xi1，xi2,…，xid),vi=(vi1，vi2,…，vid),pi=(pi1，pi2,…，pid)描述，其中i=1,2,…,m；全部种群搜索到的最优位置用pg=(pg1，pg2,…，pgd)描述；更新粒子群算法粒子位置与速度的计算式，为式(12)、式(13)。

(12)

(13)

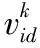
粒子群算法优化支持向量机参数c和σ的流程如下。

Step 1：归一化预处理大学英语教学效果评价数据。

Step 2：设置参数取值(最大迭代次数Tmax、加速常数c1和c2、惯性权重系数ω、种群粒子数m,c,σ的搜索范围、粒子个体的维数n)。

Step 3：对粒子群实施初始化处理。

Step 4：设置个体极值Pibest与全局极值gbest，每个粒子的适应值的计算按照粒子当前位置。计算过程如式(14)。

(14)

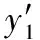
Step 5：为了生成新种群，依据粒子位置和速度更新式(12)、式(13)。

Step 6：求解新种群内每个粒子的适应度值f。

Step 7：对比以往种群最优速度、最优位置，如果优良可转换，反之则不作调整。

Step 8：如果不符合寻优结束条件，则需令迭代次数t=t+1，重返步骤Step 4，需求寻优解。

Step 9：如果寻到最小二乘支持向量机的核函数参数σ与正则化参数c最优解，则完成搜索。

1.4 粒子群算法和支持向量机的大学英语教学效果评价流程

结合大学英语教学效果评价指标体系，基于粒子群算法和支持向量机的大学英语教学效果评价模型，该模型的流程如图2所示。

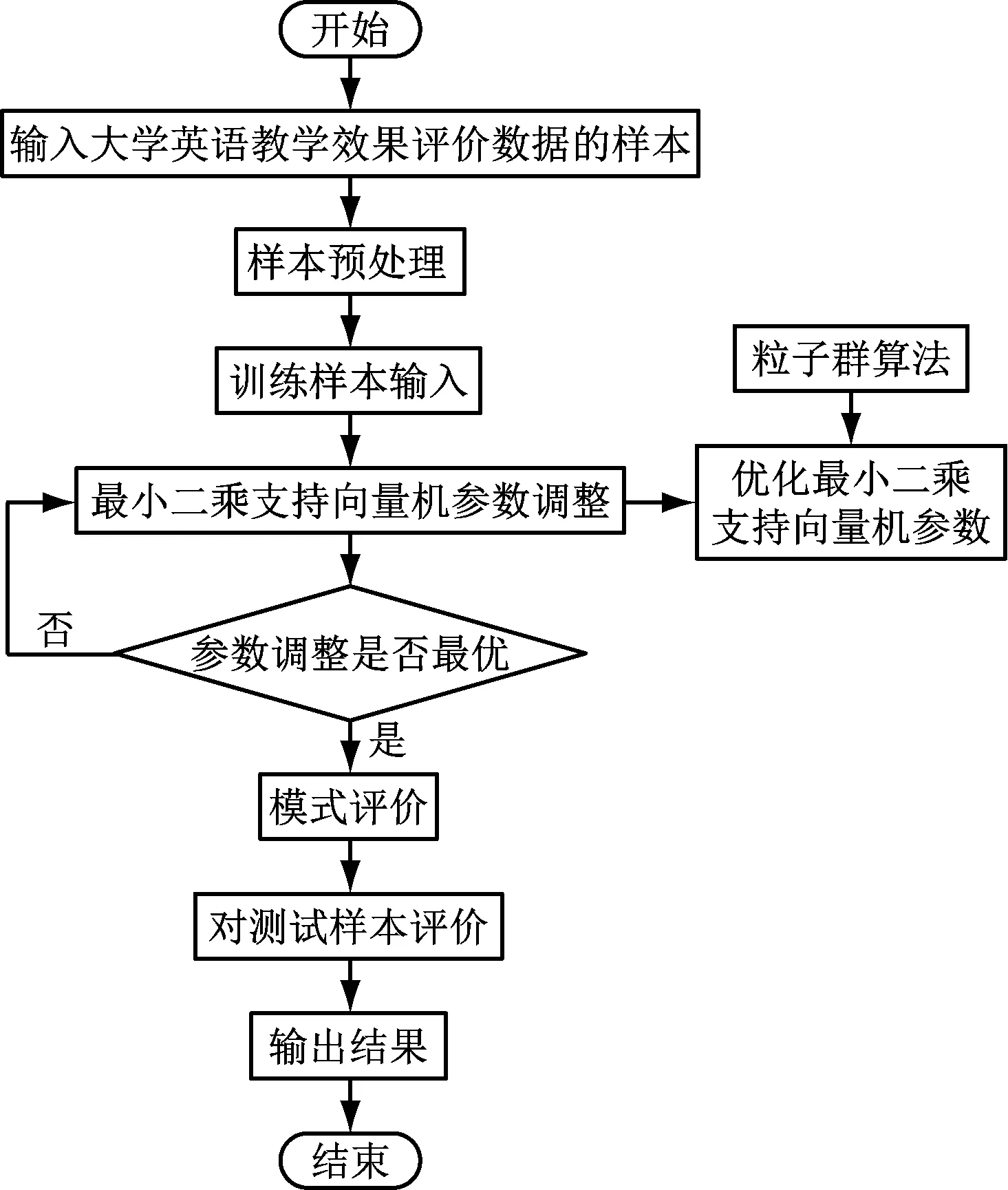
图2 基于粒子群算法和支持向量机的大学英语教学效果评价模型流程图

由图2可知，首先，输入大学英语教学效果评价数据的样本作为最小二乘支持向量机输入样本，实现大学英语教学效果评价。且采用粒子群算法求解最小二乘支持向量机的核函数参数与正则化参数最优解，优化最小二乘支持向量机评价过程。判定得出参数是否是最优解，若否，需利用粒子群算法重新调整参数成最优解，若是，对测试样品实施评价并输出结果。

2 实验结果与分析

选择某大学计算机专业的英语课堂教学效果作为研究对象，按照大学英语教学效果评价指标搜集样本数据，通过大学英语教学实际情况与专家对大学英语教学效果的评价得到大学的英语课堂教学质量等级值，并得出测试的200个数据样本，并分为10组数据集，每组20个数据样本。其中，大学英语教学效果用y描述；英语成绩用x1描述；修改作业及代课次数用x2描述，依次类推，英语课停课次数用x13描述。实验对比方法选用本文方法与文献[6]优化BP神经网络的高校教学质量评价模型方法、文献[7]基于类别加权灰靶决策的教学评价方法实施大学英语课堂教学效果实施对比测试。

采用三种方法对实验数据集实施测试，得到三种方法的准确率计算结果，如表1所示。

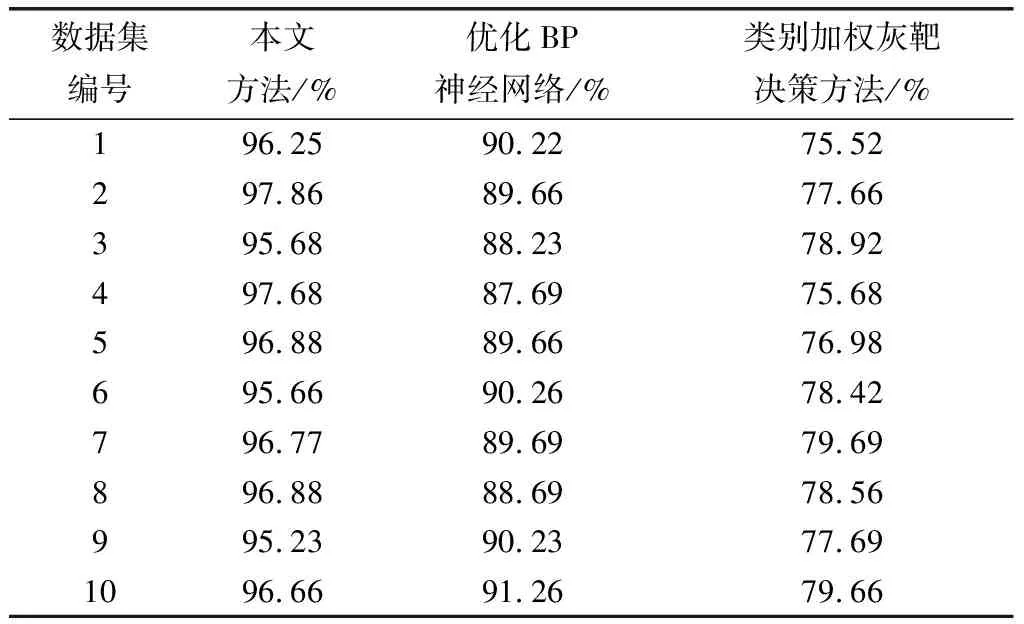
表1 评价准确率结果比较

由表1可知,本文方法平均评价准确率为96.56%，分别比优化BP神经网络的高校教学质量评价模型方法的平均评价准确率、类别加权灰靶决策的教学评价方法的平均评价准确率高出7%、18.68%。因此，本文方法的评价准确率最高。

采用三种方法对10组数据集，实施20次实验，统计实验内这三种方法的所用时间(测试时间、训练时间)，选取平均值。三种方法测试时间对比结果，如图3所示。

图3 训练时间对比结果

三种方法训练时间对比结果，如图4所示。

由图3、图4对比结果可知,本文方法在时间效率上比其他两种方法具有明显的优势，本文方法的训练时间与测试时间耗时最少，其中训练时间低至13 ms、测试时间低至5 ms。比优化BP神经网络的高校教学质量评价模型方法的训练时间最低耗时节省9 ms、测试时间最低耗时节省4 ms；基于类别加权灰靶决策的教学评价方法的训练时间最低耗时节省3 ms、测试时间最低耗时节省4 ms。

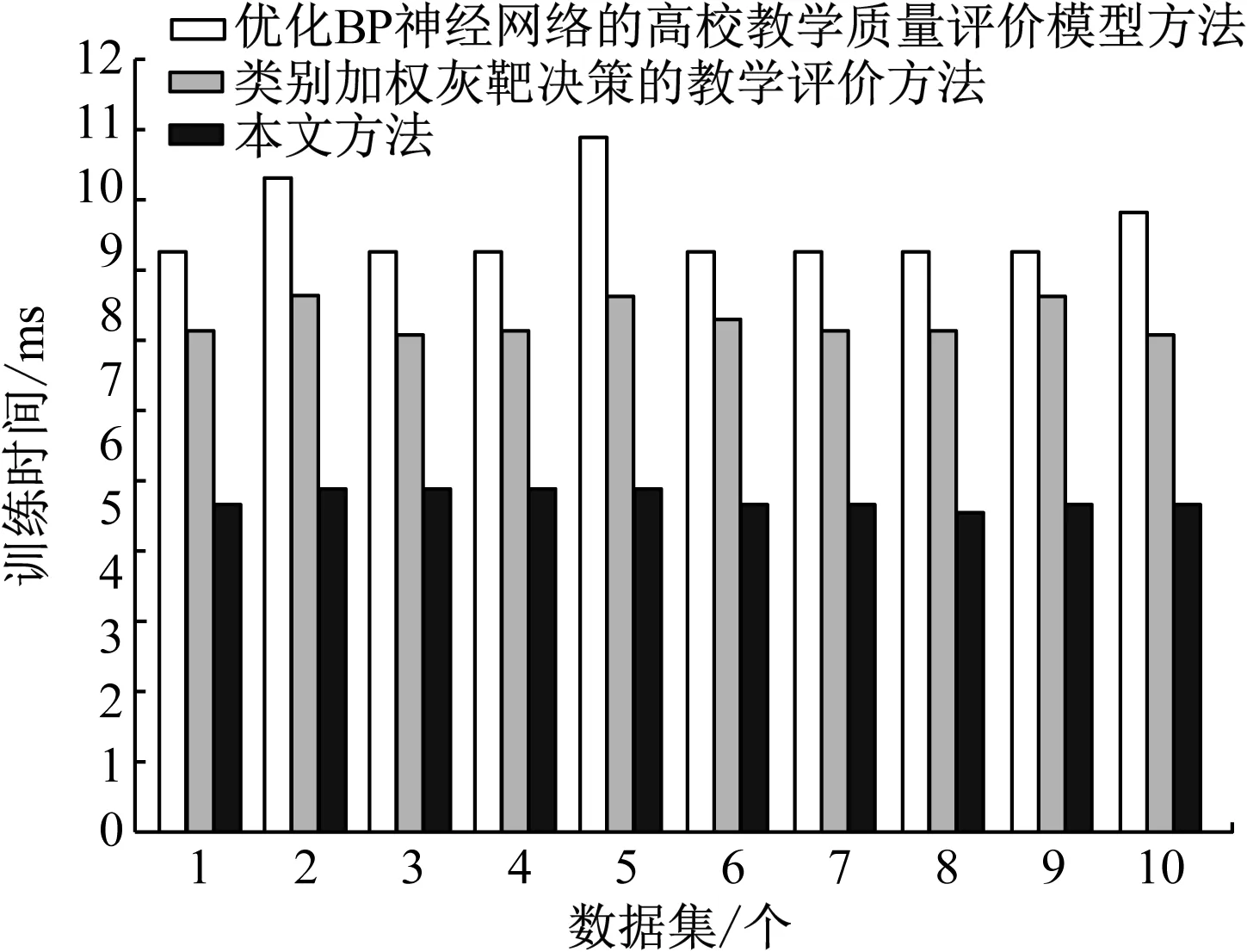
图4 测试时间对比结果

为了进一步验证本文方法的效果，采用三种方法应用在该大学的计算机专业的大学英语课堂教学中，统计该计算机专业10名学生的大学英语月考成绩，如图5所示。

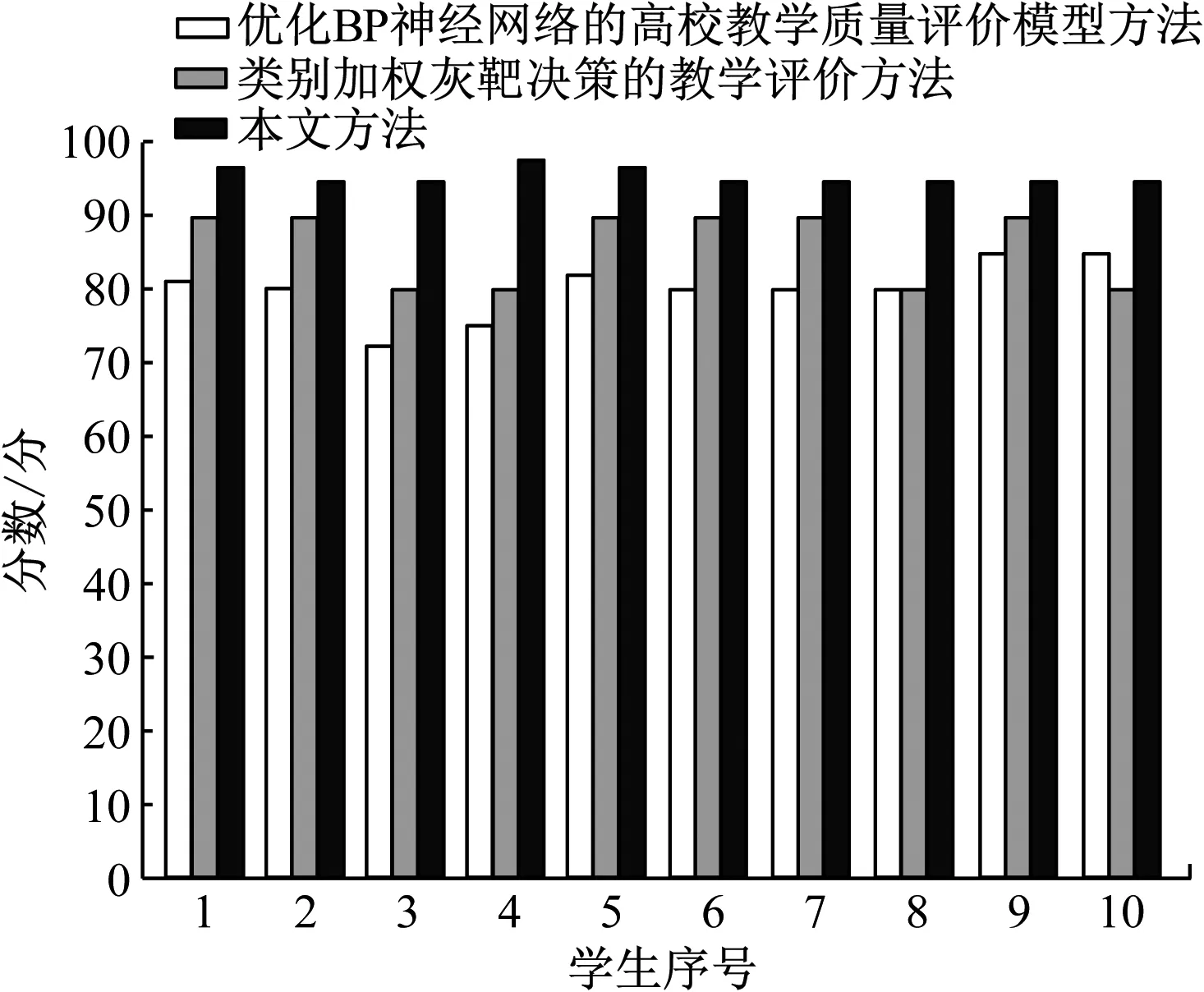
图5 成绩对比结果

由图5可知,采用本文方法的学生大学英语月考成绩比另外两种方法效果好，本文方法学生英语平均成绩为95分，比使用优化BP神经网络的高校教学质量评价模型方法后学生英语平均成绩、类别加权灰靶决策的教学评价方法的后学生英语平均成绩高出16分、9分。使用本文方法评价后学生英语成绩最高，由此可知该大学英语教师的教学效果最好。

3 总结

大学英语教学效果与各评价指标之间定量的非线性函数关系复杂，导致得到评价分值存在主观性，影响了评价的客观公正。为了精准地对大学英语教学效果进行评价，提高大学英语教学的整体水平，本文研究基于粒子群算法和支持向量机的大学英语教学效果评价模型。实验结果表明：本文方法评价准确率最高，评价时间短，评价效果最优。本文方法能提高大学生英语学习成绩，对大学英语教学水平提升具有重要的现实意义。

由于时间与精力的有限，仍然存在一些不足，有待进一步提高和完善。未来继续的研究方向为以下几方面。

(1) 为了提高研究的泛化性，需在以后的研究中，尝试应用更好的方法对大学英语教学评价指标体系深入研究，使其更加完整、科学。

(2) 对本文方法实施更多的实验数据检验，在检验中不断优化。

(3) 希望深入的学习将更好的方法应用于大学英语教学，使评价准确率及效率更好。