一种基于独立电感能量注入的无线电能传输变换器
廖文良,林再法,罗大庆,陈 林,洪剑锋,陈文芗,沈汉鑫
(1.集美大学理学院,福建 厦门 361021;2.厦门大学航空航天学院,福建 厦门 361102;3.厦门理工学院 机械与汽车工程学院,福建 厦门 361024;4.厦门理工学院光电与通信工程学院,福建 厦门 361024)
感应式无线电能传输(inductive power transmission,IPT)系统采用感应耦合技术将能量无线传输到负载,具有安全、环保、方便等优点,近年来已被广泛应用于无线电能量传输[1-4],尤其是电动汽车[5-6]的充电应用.IPT系统在原理上可看作一个松散耦合的变压器系统[7],通过一对线圈构成磁耦合链路,将能量从一次侧传递到二次侧[8].由于松散耦合变压器的磁化电感比漏电感小得多,初次级之间的耦合能力非常弱,导致无功功率高、效率和输出功率低.为了解决这一问题,在一次侧和二次侧回路中采用谐振网络来补偿漏电感所引起的无功功率[9].无功补偿方法已有许多文献进行了详细研究,如串联-串联、串联-并联、并联-串联、并联-并联[10-11]4种基本拓扑,以及电感-电容-电感[12]、电感-电感-电容[13]等混合补偿拓扑.这些工作改善了松散耦合变压器的漏电感问题,使IPT系统能够在稳定的条件下正常工作.
然而,IPT系统的实际应用场景较为复杂,是一个变参数系统,如负载变化、线圈不对准、气隙变化等.参数变化会导致谐振网络频率漂移,造成变换器与谐振网络之间失谐,效率和输出功率下降[14-15].采用锁相环(phase-locked loop,PLL)进行频率跟踪是解决失谐问题的主要方法[16-17].通过PLL,系统可以很好地跟踪频率,但是由于谐振网络与变换器之间存在强耦合,为了保证软开关条件,系统开关状态的变化只能在初级电流过零点处进行,这在很大程度上增加了开关控制策略的难度[18].
输出功率控制是IPT系统中非常重要的一项工作[19],目前主要采用频率控制[20]和移相控制[21]两种控制方法.由于变换器与谐振网络之间的强耦合,这些输出功率控制方法在实际应用场景下可能会导致系统失去软开关条件.因此,这些方法仍然存在诸如高电应力和开关损耗等问题[22-23].
本文提出一种将能量传输过程分为能量注入和自由谐振(independently inductive energy injection and free resonance,IIEIFR)两种工作模式的变换器拓扑结构.在能量注入模式中,将初级电感从谐振网络中隔离出来,并独立地与输入电源连接,输入电源独立地对初级电感注入能量.在自由谐振模式中,电感切断与输入电源的连接,并与初级补偿电容连接,构成初级谐振补偿回路,实现系统自由谐振.基于这种控制策略的变换器拓扑,输入电源与谐振网络之间被完全解耦,具有以下两个优点:1) 输入电源对系统能量注入的节拍不再受谐振频率的约束,可消除无功功率并解决频率跟踪难和系统失谐的问题;2) 在能量注入模式中,能量被独立注入到电感中,采用基于模态时间调节的输出功率控制方法,通过调节能量注入时间对输出功率进行控制,实现输出功率控制不受谐振网络的影响,解决了IPT系统输出功率控制难的问题.
1 拓扑与建模
IIEIFR的IPT系统拓扑结构如图1所示,其中:UDC为输入电源;iB为母线电流;T为初级线圈与次级线圈构成的松散耦合变压器;L1为初级线圈电感,L2为次级线圈电感,初级与次级之间的耦合系数为k;ip和is分别为初级线圈和次级线圈的电流;Cs为次级谐振电容,与L2构成串联谐振补偿回路;R为负载电阻;uo为负载两端电压;S1和S2为金属氧化物半导体场效应晶体管(MOSFET)或绝缘栅双极型晶体管(IGBT),S1、S2不能同时导通;D1和D2分别为S1和S2的体二极管,D0为反回流二极管;Cp为初级谐振电容,但它没有直接与L1组成初级补偿回路,是否与L1连接取决于S2的导通情况;控制器用于控制系统运行,并根据电压传感器的输出信号U与电流传感器的输出信号I产生开关控制信号g1和g2,分别控制S1和S2的导通与截止.

图1 IIEIFR IPT系统拓扑结构Fig.1 System topology structure of IIEIFR IPT
系统工作时分为3个模态:当S1导通时,S2截止,L1被连接到UDC,产生母线电流iB,初级线圈被独立地注入能量,这个模态称为能量注入模态.当S1截止,S2导通时,L1被连接到Cp,与Cp构成并联谐振补偿回路,系统开始自由谐振,这个模态称为自由谐振模态.系统自由谐振时,UDC与谐振回路隔离,母线电流iB=0.当S1与S2都截止时,L1既没有与UDC连接,也没有与Cp连接,初级回路没有电流流过,这个模态称为截止模态.能量注入模态与自由谐振模态中,能量通过松散耦合变压器送往次级,而在截止模态中,没有能量传输.为了提高效率,截止模态可以被取消掉.
将图1中松散耦合变压器T用变压器T型等效模型替换,可得到IIEIFR的IPT系统T型等效模型,如图2所示,其中Lp和LS分别为初级和次级的漏感,Lm为励磁电感.
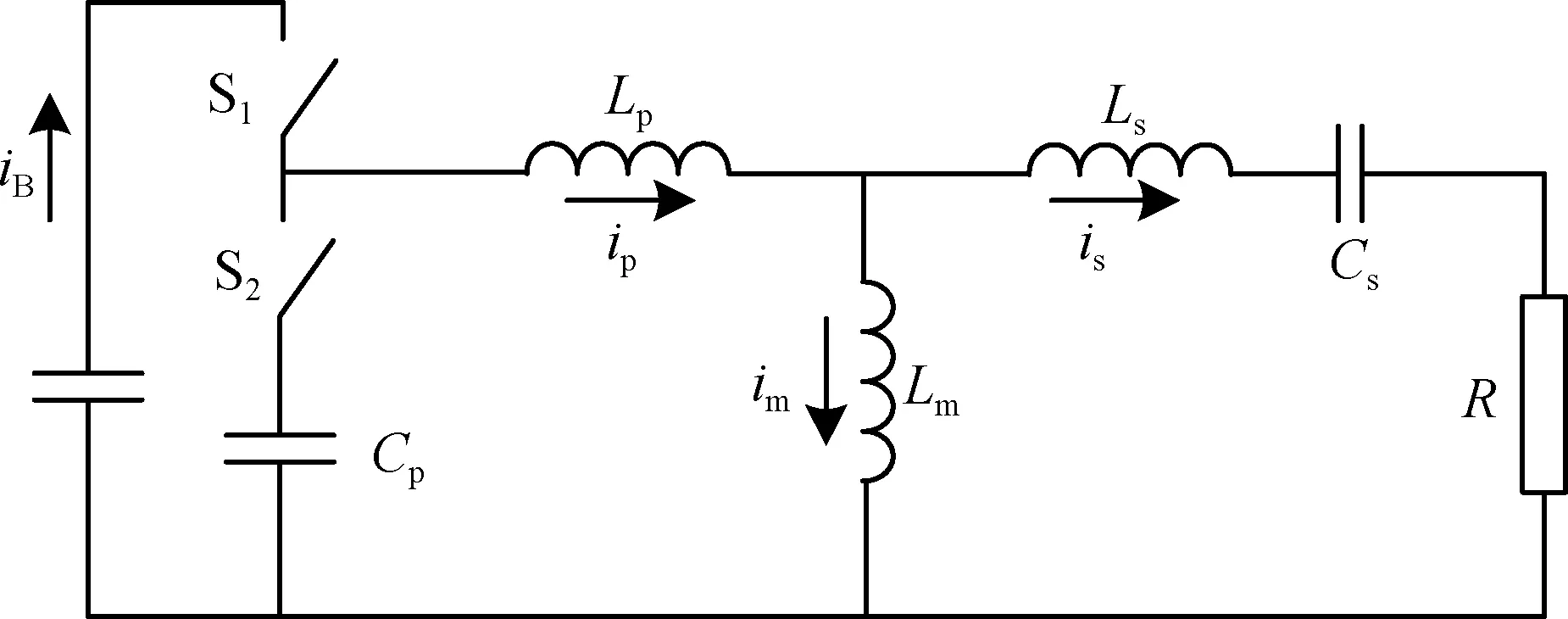
图2 IIEIFR的IPT系统的T型等效模型Fig.2 T type equivalent model of IIEIFR IPT
假设初级线圈与次级线圈匝数相同(n1=n2),电感相同(L1=L2=L),根据松散耦合变压器理论,有如下关系:
(1)
其中,M为耦合电感,k为耦合系数.
当S1截止、S2导通时,UDC断开与L1的连接,停止向系统注入能量,iB为0.此时L1通过S2与初级谐振电容Cp相连,形成谐振网络,系统进入自由谐振模态.由于系统已经谐振,所以图2可进一步用阻抗模型描述,如图3所示.

图3 自由谐振模态系统的等效模型Fig.3 Equivalent model of free resonant modal system
图3中,Zr为次级反射到初级的等效阻抗,Zp为初级回路阻抗,具体计算为:
(2)
整理式(2),可得:
(3)

(4)
2 模态分析
虽然IIEIFR的IPT系统工作过程由3个模态组成,但为了保证模态转换过程中系统处于软开关工作环境,需要在能量注入模态与自由谐振模态之间、自由谐振模态与截止模态之间分别插入一个过渡模态.因此,IIEIFR的IPT系统在工作时可细分为5个工作状态.图 4是系统工作状态转换图,图中每一个工作状态都用带圈的数字标识,状态之间的转换顺序用箭头标识,有流过电流的电路和元件用黑实线标识,无电流流过的电路和元件用虚线标识.

图4 系统工作状态转换图Fig.4 System working state transition diagram
为了更直观地进行分析,将ip、iB、ucp以及S1、S2的驱动电压的波形放在图 5中.作为参照,图 4中的各个状态相应地被标识在图 5中.

图5 S1、S2的驱动电压和ip、iB、ucp的波形Fig.5 Waveform of driving voltage for S1,S2 and ip,iB,ucp
结合图4和5,下面对5个工作状态进行分析:
状态①[t0,t1),这个状态为能量注入模态,此时S1导通、S2截止,UDC与L1相连,Cp与L1隔离.在这个状态中,UDC通过S1独立地向L1注入能量,iB与ip线性地上升,初级电感的磁场能量增加.在该模态中电容处于隔离状态,ucp维持在截止模态时的电压.在状态①中,一部分能量通过耦合被送往次级.根据图2,可列出状态①的回路方程:
(5)
从图5可以看到在t0时刻有ip(t0)=0,为了分析方便,假设t0=0.结合图 2和式(1),可得到方程(5)的初始条件为:
(6)
利用式(6)的初始条件求解式(5),可解得初级回路电流ip为

θ1),
(7)
其中:
(8)
考虑到在大多数使用场合中,如电动汽车充电系统,IPT系统的耦合系数都很低(k<0.3)[24],式(7)中的第2项和第3项可以忽略.因此,式(7)可简化为
(9)
式(9)表明在状态①(能量注入模态)中,L1中的电流从0开始线性上升,其上升斜率取决于UDC与初级电感L1.假设t0=0,t1-t0=τ,则在能量注入模态结束时,初级线圈中的电流为
(10)
根据式(10),在能量注入模态结束时,注入系统的能量为
(11)
式(11)表明,注入系统的能量只与能量注入时间τ有关,因此可以通过调节τ对系统功率进行控制.
状态②[t1,t2),在这个状态中S1、S2均截止,UDC断开与L1的连接,iB下降为0,D2导通为ip续流.D2导通后,初级电容Cp与L1连接在一起形成谐振,为进入自由谐振模态做好了准备.因此,这个状态是系统从能量注入模态转向自由谐振模态中的过渡状态.在这个状态中,因为UDC停止了对初级线圈的能量注入,ip正弦式地下降.
为了让系统进入完整的自由谐振模态,就必须在合适的时候导通S2以保证ip能够双向流动.由图5可知,ip的过零点Tp2是一个关键点.在[t1,Tp2]区间内ip均大于0,D2导通.D2的导通为S2提供了一个软开关导通的条件,因此可以定义Tp2-t1为S2的导通时间裕度Tm1.在Tm1中选择合适的时刻t2导通S2,为ip提供双向流动的通道,就可在软开关条件下将系统由能量注入模态转入到自由谐振模态.
状态③[t2,t3),在这个状态中S2处于导通状态,系统正式进入自由谐振模态.当谐振槽中的能量下降到一定程度后,继续维持谐振的意义已经不大,需要将系统由自由谐振模态转换到截止模态.本文中以Cp两端的电压作为系统退出自由谐振模态的评价参数,当Cp电压ucp下降到UDC后,系统退出自由谐振并转入截止模态.
状态④[t3,Tp4),当ucp幅值达到UDC后,在t3时刻关断S2.S2被关断后,ip反向流动的通道被截断,无法反向流动,为系统进入截止模态做好准备,因此这个状态是系统由自由谐振模态转向截止模态的过渡模态.由于在自由谐振模态中,磁场能量与电场能量相互转换,简单的关断S2可能会产生过大的电应力,因此如何正确的选择t3非常重要.
由图 5可知,在Tp3时刻ucp的幅值接近UDC,系统可以退出自由谐振模态.也就是说t3应该选择在Tp3之后关断S2.Tp3时刻对应ip的过0点,之后ip维持正向流动一直到另一个过0点Tp4.在[Tp3,Tp4]中,D2都处于导通状态.定义Tp4-Tp3为S2的关断时间裕度Tm2,在Tm2内S2满足软开关操作条件.因此,可在Tm2内选择t3关断S2,让系统进入退出自由谐振模态的过渡模态.
S2被关断后,ip依然可以通过D2继续流动.这个过程中电感中的磁场能量减少,电容中的电场能量增加.当时间到达Tp4后,ip下降到0.Tp4之后,ip缺少反向流动的通道,电容中的电场能量无法反向传输,因此ip=0且ucp维持在-UDC上,系统转入截止模态.
状态⑤[Tp4,t4),这个状态就是截止模态,S1和S2都被关断,ip=0;ucp=-UDC.
显然,自由谐振模态是由状态②、③和④组成,可放在一起分析.在区间[t1,t4]内,系统可用图3所示自由谐振模态等效模型表示,根据文献[23,25]所采用的分析方法,ip的解为
ip=Ipme-α tsin(ωt+θ),
(12)
其中,α=2L/R,ω由式(4)确定,而幅值Ipm和相位角θ是两个未知数,需要求解.利用式(12),可得以下方程:
(13)
设t1=0,则在t1时刻有ip(0)=ip(t1)=ip(τ)·ucp(0)=-UDC.将这初值代入式(13),可求解出这两个未知数为:
(14)
3 实验平台
为了验证本文提出的电路拓扑结构和理论分析,根据图1搭建了一个IPT系统,如图6所示.其中,控制器以STM32处理器为核心组成.为了减少对次级补偿网络的影响,负载电阻采用无感电阻.实验平台其他主要元器件参数列在表1中.

图6 系统实验平台Fig.6 System experiment platform

表1 元件参数Tab.1 Component parameters
初级和次级线圈的结构相同,如图7所示.其结构为:线圈基底为环氧树脂板,在基底上放射状地排布铁氧体片(型号PC40)作为磁芯,在磁芯上用利兹线(直径500 mm×0.1 mm)绕成线圈,最后在线圈上面盖上有机玻璃板做防护层,其几何尺寸如表2所述.初级线圈和次级线圈构成一个松散耦合变压器进

图7 初级和次级线圈的结构图Fig.7 Structure of primary and secondary coils

表2 线圈几何尺寸
行无线能量的传递,两者之间的互感耦合系数k随着发射接收线圈之间空隙距离d的变化而发生改变,采用驿生胜利科技的LCR仪VC4091(中国、深圳)对搭建的磁耦合系统进行测量,线圈电感量为640 μH,品质因数值为300.图8为耦合系数与发射接收线圈之间空隙距离的关系曲线,可见当d从5 cm变化到21 cm 时,k从0.52变化到0.08.电动汽车无线充电作业中,k值的变化范围为0.10~0.33[26],本实验所搭建的耦合系统涵盖这一范围,能够正确地反映电动汽车无线充电的实际情况.

图8 耦合系数与气隙间距的关系Fig.8 Coupling coefficient versus air gaps
4 仿真及实验验证
4.1 特性验证
在UDC=100 V,τ=50μs,R=20 Ω,k=0.3的条件下,对图1所示的拓扑进行仿真和实验,其中仿真软件为Saber Sketch,实验中所用示波器为SDS1104CFL(中国,鼎阳);功率分析仪为WT500(日本,YOKOGAWA),元器件的参数值与表1一致, 仿真结果与图5一致.实验结果如图9所示,由于示波器输入端口数有限,只能显示S1和S2驱动电压波形以及ip和iB波形.

图9 实验结果Fig.9 Experiment result
[t0,t1)区间为系统的能量注入模态,ip线性上升,在t1时刻达到峰值.能量注入模态结束后(t1之后),系统进入自由谐振模态.[t1,T4]区间是系统自由谐振模态.S2导通时刻t2处于T2与t1之间,即处于软导通时间裕度Tm1之中.S2关断时刻t3处于T3与T4之间,即处于软关断时间裕度Tm2之中.由图9可知,实验结果与理论波形相吻合.
图10为S2软开关工作条件实验结果.其中iS2为流过S2的电流曲线,US2为S2的压降曲线.由于示波器探头共地的问题,S1压降曲线不能与S2压降曲线同时被采集下来.虽然图 10中没有显示S1的控制信号,但从它对其他波形干扰的波形分析,依然可以看出S1导通和关断的时刻.从图10中可以看到,S2管压降的特点为:在能量注入模态期间[t0,t1)为UDC;在截止模态(S1、S2均截止,[T4,t0))期间,由于寄生参数的作用产生寄生振荡;在自由谐振模态期间为0.进一步可以看到,S2的导通时刻t2、关断时刻t3都处于自由谐振模态中,其压降都为零,因此它的开关时刻都处于零电压软开关调节.

图10 S2软开关条件实验结果Fig.10 Experiment results of S2 soft switching conditions
4.2 功率控制
为了验证所搭建的IPT系统功率控制能力,在不同条件下进行功率测试实验和效率分析,如图11所示.

图11 输出功率与能量注入时间之间的关系Fig.11 The relationship between output power energy and injection time
图11(a)和(b)为UDC=100 V,R=20 Ω时,不同耦合系数k条件下,输出功率和传输效率与能量注入时间之间关系的实验结果.输出功率与能量注入时间之间接近线性关系.当k=0.2时,能量注入时间由30 μs 增加到50 μs时,实际输出功率从21.76 W增加到53.96 W;相同条件下,随着k的增大,实际输出功率基本保持不变,偏差在8%以内,传输效率为83%~89%.通过实验和理论计算表明,输出功率P主要与能量注入时间相关,符合式(11),与耦合系数相关性不大.
图11(c)为UDC=100 V,k=0.5时,不同负载条件下,输出功率与能量注入时间之间关系的实验结果,可见输出功率与能量注入时间接近线性关系.当R=10 Ω时,能量注入时间由30 μs增加到50 μs时,实际输出功率从23.77 W增加到55.86 W;相同条件下,随着负载的增大,实际输出功率基本保持不变,偏差在1%以内,不同负载的实际输出功率曲线接近重合.通过实验和理论计算表明,输出功率主要与能量注入时间相关,符合式(11),与负载相关性小.
图11(d)是在R=20 Ω,k=0.5,不同输入电压条件下输出功率与能量注入时间之间关系的实验结果,输出功率与能量注入时间接近线性关系.当UDC=100 V时,能量注入时间由30 μs增加到50 μs时,实际输出功率从23.84 W增加到56.47 W;相同条件下,随着输入电压的增大,输出功率与能量注入时间基本保持线性关系.通过实验和理论计算表明,输出功率主要与能量注入时间相关,符合式(11).
5 结 论
本文提出了一种应用于IPT系统的变换器,该变换器采用能量独立注入与自由谐振两种模式的控制策略.通过这种策略,能量传输过程可被分为能量注入与自由谐振两个独立的过程,因此由该变换器组成的IPT系统具有以下特点:1) 变换器与谐振网络解耦,在能量注入模态中输入电源可独立地向初级电感注入能量,能量注入过程不受其他因素影响,而且可通过控制能量注入时间控制输出功率.2) 自由谐振模态中可规划出两个对开关进行操作的时间裕度,这两个时间裕度可保证变换器的开关处于软开关操作条件.
仿真和实验结果验证了在能量注入模态中电源独立地向初级电感注入能量、在自由谐振模态中输入电源被隔离、谐振网络独立地进行自由谐振的理论分析;所采用的控制策略能够保证开关管在系统模态转换过程中都处于软开关工作条件.通过不同耦合系数、不同负载、不同输入电压环境下的实验结果证实了理论分析的正确性,输出功率与耦合系数、负载相关性小,可通过控制能量注入时间的长短,独立地对输出功率进行控制.

