基于改进PSO算法的6R机器人逆运动学分析
李西宸,孙 晓,李文杰,曾 成
1 研究背景
工业机器人是现代制造业中一种重要的机电一体化设备,已被广泛地应用于电子、物流、化工等各工业领域中。其中,6R 机器人因具有工作空间大、运动灵活、非冗余等特点,成为机器人应用和研究的首要目标[1]。逆运动学是已知机械臂末端位置,求解每个关节的角度,其解有多个,其方程组具有高维、非线性的特点,求解过程复杂且不易求出正确解[2]。逆解问题是机器人研究的重点问题之一,是机器人轨迹规划与运动控制的基础。很多学者在该领域进行了研究,且提出了许多理论与方法,如解析法[3]、几何法[4]、智能算法[1]等。
机器人逆运动学的多解虽然能够通过解析法和几何法获得,但是前提是其必须满足特殊的结构。随着机器人结构的复杂化和计算机技术发展的突飞猛进,许多学者将智能优化方法应用于机器人逆运动学求解问题中,其主要思路是将机器人运动学方程转化为优化控制问题加以解决[5]。此类智能算法主要包括遗传算法、粒子群优化算法(particle swarm optimization,PSO),以及退火算法等[6]。林阳等[7]针对6R 机器人,提出了一种基于多种群遗传算法的逆运动学求解方法。与封闭解法和数值解法相比,多种群遗传算法结构简单,无需进行矩阵逆运算以及三角函数运算,可以精确地解决任意自由度的一般机器人逆运动学问题。多种群遗传算法虽然解决了传统单种群遗传算法的局部收敛和“早熟”等问题,提高了系统的收敛速度,但是在其他方面,如精度上,仍然存在较大的问题。
国内外已有相关研究中,主要将全局学习因子和局部学习因子联合起来,通过调整比例系数和全局学习因子的比例以获得更快的收敛速度;或以“目标点位姿误差最小”为目标函数,各关节转角极限为约束条件,利用PSO 算法,求解机器人的最优逆解。虽然PSO 算法具有操作简单、参数较少、收敛速度较快等特点,在函数寻优、图像处理、大地测量等众多领域得到了广泛的应用,但是在求解逆向运动学方面,其仿真实验中仍然存在不稳定和局部最优与种群单一的问题[8]。
为解决传统PSO 算法在求解逆向运动学中存在的不稳定问题和易陷入局部最优与种群单一的问题,本文提出一种改进的PSO 算法。该算法中引入动态权重因子,即动态权重调整因子结合CMA-ES(covariance matrix adaptation evolutionary strategies)算法[9]的步长更新方法,以平衡全局搜索能力和局部搜索能力,防止陷入局部最优,并且提高种群多样性;同时,引入收缩学习因子,以提高算法的搜索能力,得到高质量的解,防止在迭代过程中陷入局部最优。并以REBot-V-6R 机器人为例,首先用螺旋理论进行正向运动学建模,将机器人逆运动学求解的问题转换为改进PSO 算法的寻优问题;其次验证改进PSO 算法求逆运动学解的可行性;最后分别对REBot-V-6R 机器人的位置误差、姿态误差进行仿真,以验证所提算法的有效性。
2 正向运动学分析
本研究针对实验室引进的REBot-V-6R 机器人进行仿真验证。图1 所示为REBot-V-6R 机器人的实物图与其结构简图。
图1 中,{S}为惯性坐标系,{T}为工具坐标系,且{T}的原点与关节6 的原点重合。x、y、z为坐标轴,d为杆长,θ为旋转角度。
利用螺旋理论对机器人进行正向运动学建模,表1 为各关节螺旋轴的参数,其中i为杆的序号;ωi为旋转轴的方向矢量;ri为距离;d1~d6为杆长。

表1 REBot-V-6R 的各关节螺旋轴参数Table 1 Spiral axis of each joint of REBOt-V-6R
工具坐标系建立在机器人的第5 关节处,由图1可知,机器人处于0 位时,工具坐标系的初始位姿为
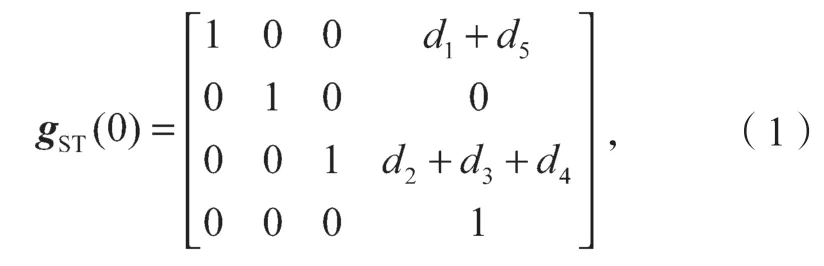
机器人正向运动学方程为
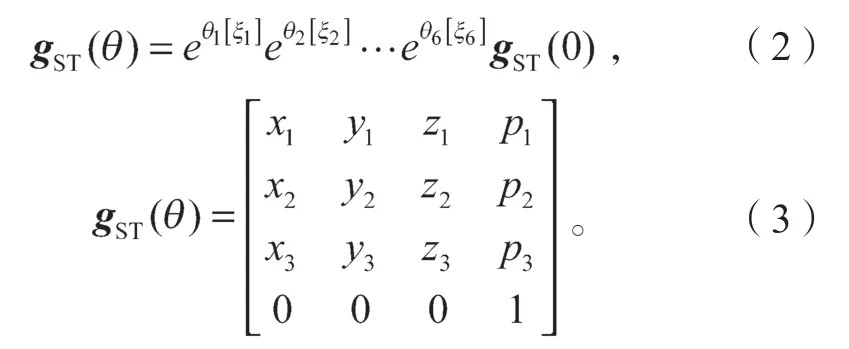
式中:
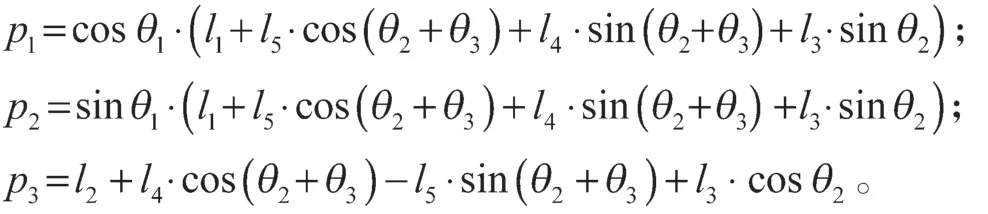
3 改进PSO 算法
3.1 经典PSO 算法
PSO 算法,是通过模拟各种鸟类群体之间的其他鸟类个体进行相互觅食竞争活动的行为而进行设计和研究发现的,一种非常智能的群优化粒子算法分析工具,可以通过它搜索各群体中的鸟类个体之间的相互协作或与其他各群体之间的相互竞争的活动关系,还可以帮助实现在复杂空间内得到最优化的解。
PSO 算法的收敛速度较快,易于实现,并且仅有少量的参数值需要进行调整,其中,具有较好的应用前景的技术领域,主要包括多目标性问题的优化、归纳、模型识别、生物体系建模、信号处理、决策、仿真及模拟等。粒子群优化算法起步于一种由粒子和粒子间形成的社会系统,该社会系统的研究主要侧重于简单的由个体所构建的群落和环境之间的相互作用,以及各类人与个体之间的相互作用和行为。
PSO 的相关技术理论发展史尚短,在其技术理论的一定基础和实际应用推广等方面仍然存在一些亟待解决的问题。如当PSO 被应用于高维复杂问题的优化时,它往往会过早收敛,也就是说,在找到全局最优解之前,种群已经聚集到一个停滞点,这些早熟的收敛点可能是局部极小点,也可能是局部极小点附近的点[10]。因而,对于PSO 算法的早熟收敛行为的深入研究,可以在一定程度上为PSO 算法的进一步完善与发展奠定理论基础。
PSO 算法是随机地产生一个原始的种群,并且给这个种群中每个粒子都提供了一个随机的位置和随机的速度,在粒子的飞行过程中,其位置和运动速度可以通过自身和其他同伴的飞行经验来进行动态调整,最终使得全体种群粒子都飞向目标位置[11]。
设xi=[xi1,xi2,…,xin]为粒子i的当前位置;vi=[vi1,vi2,…,vin]为粒子i的当前飞行速度;pi=[pi1,pi2,…,pin]为粒子i所经历的最好位置,也称个体最好位置;pg=[pg1,pg2,…,pgn]为所有粒子经历的最好位置,也称全局最优位置。
PSO 算法的速度和位置更新公式如下:
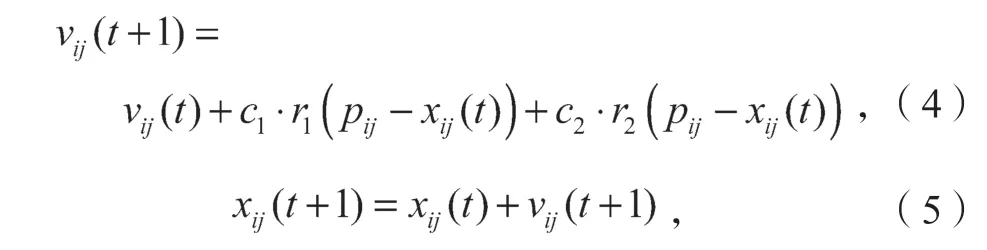
式(4)(5)中:t为当前迭代次数;
c1、c2均为学习因子;
r1、r2为2 个相互独立且均匀分布的(0, 1)间的随机数。
经典PSO 算法主要采用“速度-位置”搜索模型来帮助解决优化问题。每一个粒子都可以被认为是解空间里面的潜在解,并且可以通过对解的适应值进行分析来判断这个解的效果[12]。经典PSO 算法在初期就具有较快的收敛特性,但随着粒子进行了同一化,往往很容易达到局部最优。
3.2 动态权重因子
惯性权重调整策略大多采用线性或者非线性递减模式,这种单调的演变模式存在以下不足:首先,若算法的迭代次数很大,则每次迭代所引起的惯性权重改变量很小,以致惯性权重调节功能的发挥效果不明显;其次,这种单一的调节模式减少了种群多样性。因此,本研究引入如下结合CMA-ES 算法中步长更新方法的动态权重调整因子,对惯性权重进行动态调整:
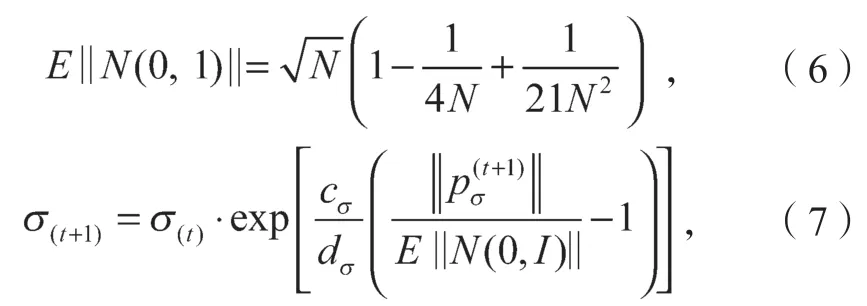
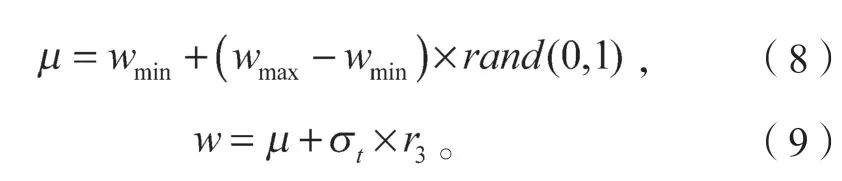
式(6)~(9)中:E||N(0,1)||为归一化进化路径在随机选择下的期望长度,N为正态分布;
σ为步长;
cσ为pσ的更新学习率;
dσ为接近于1 的阻尼系数;
μ为中间变量;
w为惯性权重;
rand为(0, 1)随机数;
r3为服从正态分布的(0, 1)随机数;
通过式(6)~(9)动态更新惯性权重,动态平衡全局搜索和局部搜索能力,有效防止其陷入局部最优,并提高种群多样性。
引入如下惯性权重粒子速度更新公式:

3.3 收缩学习因子
PSO 算法能有效地解决一些简单的和小规模的约束优化问题,但是在面对复杂和多目标的系统优化时,很容易产生“趋同性”问题,从而使得种群多样性损失过快,最终导致算法过早收敛和未能搜寻到最优值。对此,可以通过设定合适的收缩因子,提高算法的搜索能力,加快收敛速度。为了有效搜索不同区域,且防止在迭代过程中陷入局部最优,引入如下收缩学习因子。
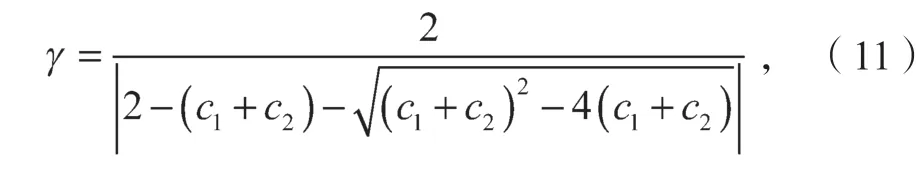
其中,c1+c2>4。
这种改进算法经实验验证后确定,当公式中的参数取c1=2、c2=2.1 时,收缩因子效果较好,能得到优质的解,且能够满足收敛速度与精度。
引入收缩学习因子后,粒子每次迭代按照式(5)(11)(12)来改变自身的位置和速度:
4 逆运动学求解
4.1 适应度函数的建立
机器人手腕的位置可以由前3 个关节确定,其最终姿态由后3 个关节确定,所以采用臂腕分离的方式建立适应度函数[2]:

式(13)(14)中:fitness1为目标位置pdes与实际位置pcur之间的误差;
fitness2为目标姿态xdes与实际姿态xcur之间的误差。
4.2 改进PSO 求解机械臂运动学逆解
在用改进PSO算法求解机械臂逆运动学过程中,粒子i由上述6 个关节角变量构成,即粒子i的位置向量表示为,每个位置向量代表逆运动学问题的一个候选解;粒子i的速度向量用表示。
改进PSO 算法求机械臂运动学逆解流程图如图2 所示。
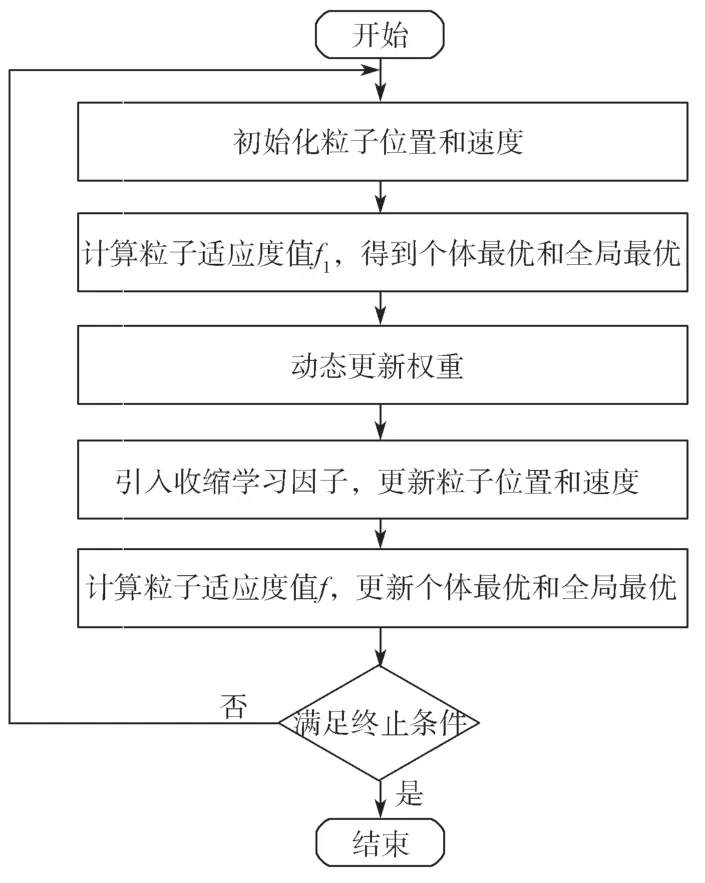
图2 改进PSO 算法求解流程图Fig.2 Flow chart of improved PSO algorithm for a solution
改进的PSO 算法求解机械臂运动学逆解的详细步骤描述如下。
步骤1 初始化粒子的位置和速度,设置粒子位置与飞行速度的范围、种群规模m、最大进化迭代次数。
步骤2 通过适应度值计算,得到个体最优pb和全局最优pg;计算粒子i(i= 1, 2,…,m)的适应度值f,且将粒子的初始位置设置为该粒子i的历史最佳位置,将种群的初始最佳位置设置为种群全局历史最佳位置。
步骤3 进行迭代循环,采用动态权重调整因子结合CMA-ES 算法步长更新方法,通过公式(6)~(9)更新权重w。
步骤4 引入收缩学习因子,以提高算法搜索能力和得到高质量解,防止迭代过程中陷入局部最优;粒子的位置和速度按公式(5)(11)(12)更新。
步骤5 计算粒子的适应度函数值f,更新个体最优pb和全局最优pg。
步骤6 未达到终止条件则执行步骤2,满足终止条件则结束循环。
5 仿真算例
为检验改进PSO 算法在求解REBot-V-6R 机器人逆向运动学解的可行性与有效性,同时采用遗传算法、经典PSO 算法以及改进PSO 算法,分别对求解REBot-V-6R 机器人的位置和姿态逆运动学进行仿真运算与分析。
5.1 参数设置
本实验计算机硬件环境如下:Intel I5 10400F、2.9 GHz、8 GB 内存;软件环境为以Matlab R2018b 进行编程,Windows 10 操作系统。
遗传算法种群大小Size= 500,交叉概率Pc=0.9,自适应变异概率Pm= 0.1-[1:1:Size]×0.01/Size,其中Size为种群大小;两种PSO 算法粒子的种群大小Size=30;wmax=0.9,wmin=0.4;c1=2,c2=2.1;初步步长σ=0.65;各关节角范围为[-π, π];算法终止条件均设为进化代数genmax=100;REBot-V-6R 机器人各杆长d1=100 mm,d2=320 mm,d3=290 mm,d4=121 mm,d5=310 mm,d6=112.5 mm。
5.2 位置误差仿真
对REBot-V-6R 机器人进行仿真比较,设置初始角(rad)Q1=[1; -1.5; 2; 1; 2; 3];Q2=[-1; 1; 2.1;1.5; -2; 3];末端位置为P1=[76.067 83; 118.468 63;298.079 36];P2=[21.247 90; -33.091 64; 342.902 31];将算法独立计算求解100 次,所得位置误差进化曲线见图3。
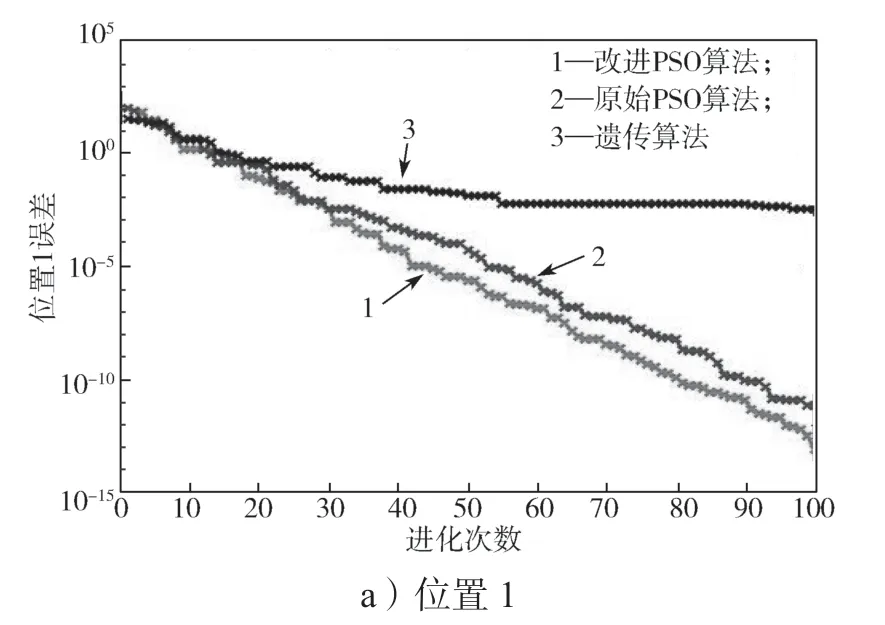
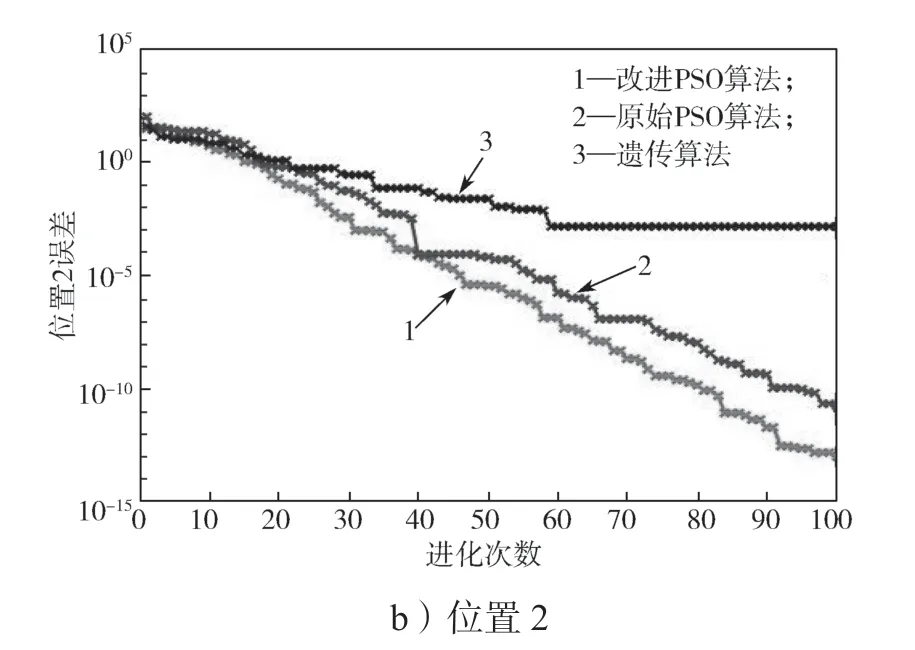
图3 位置误差进化曲线图Fig.3 Evolution curves of position errors
图3 所示3 种算法在两个位置独立运行100 次的f1结果表明,经典PSO 算法和改进PSO 算法的求解精度和速度都优于遗传算法的,且改进PSO 算法比经典PSO 算法的平均收敛精度更高。
将3 种算法在两个位置分别独立进行100 次逆解运算,各算法寻优结果中的最大适应度值、最小适应度值和平均适应度值,即位置误差最大值、最小值与误差平均值的具体数据如表2 所示。
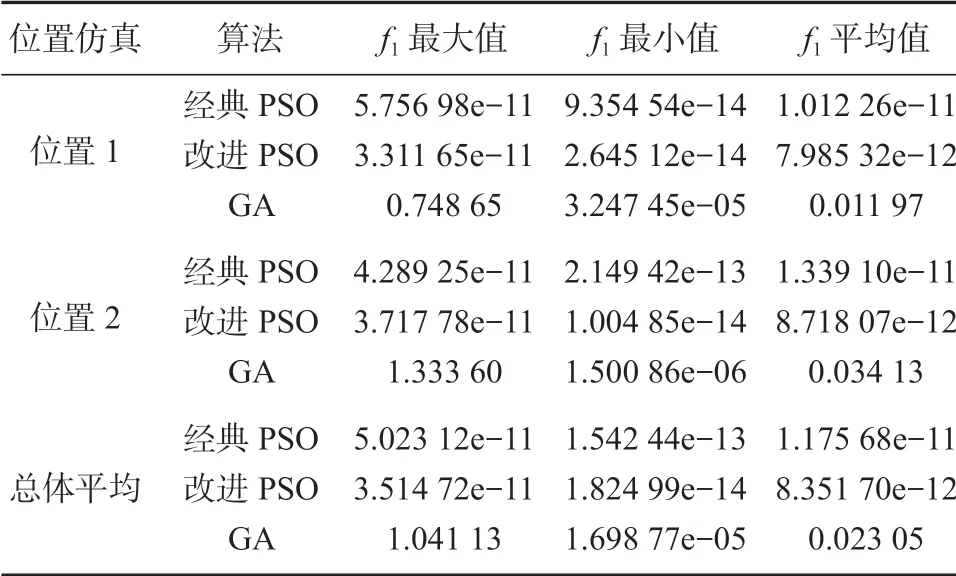
表2 3 种算法在位置1、2 独立运行100 次的结果Table 2 Results of 100 independent runs of position 1 and position 2 under three algorithms
分析表2 所示3 种算法在位置1、2 独立运行100 次的位置误差值,可以得知,改进PSO 算法和经典PSO 算法的总体误差平均值分别为8.351 70e-12与1.175 68e-11,而遗传算法的总体误差平均值为0.023 05。这一结果表明,经典PSO 算法和改进PSO算法的平均求解精度明显优于遗传算法的,且改进PSO 算法比经典PSO 算法的平均收敛精度更高。改进PSO 算法的总体平均最小误差值和平均最大误差值分别为1.824 99e-14 和3.514 72e-11,而经典PSO算法的总体平均最小误差值和平均最大误差值分别为1.542 44e-13 和5.023 12e-11。遗传算法的总体平均最小误差值和平均最大误差值分别为1.698 77e-05和1.041 13。由此可得,利用改进PSO 算法进行机器人逆运动学求解时,改进PSO 算法的稳定性高于经典PSO 算法的,且远高于遗传算法的。以上结果表明:PSO 算法在机器人逆运动学求解时,其求解精度与稳定性上都有很大的优势。改进PSO 算法在寻优稳定性和寻优精度上都比经典PSO 算法的有所提升。
5.3 姿态误差仿真
对REBot-V-6R 机器人进行仿真比较,设置初始角(rad)Q1=[1; -1.5; 2; 1; 2; 3];Q2=[-1; 1; 2.1; 1.5; -2;3];将算法独立计算求解100 次,所得姿态误差进化曲线如图4 所示。

图4 姿态误差进化曲线图Fig.4 Evolution curves of rotation errors
图4 所示3 种算法在两个姿态独立运行100 次的f2结果表明,经典PSO 算法和改进PSO 算法的求解精度和求解速度都优于遗传算法的,且进化曲线表明,改进PSO 算法比经典PSO 算法的全局搜索能力明显增强;收敛速度更快,鲁棒性较高。
将3 种算法分别独立进行100 次逆解运算,各算法寻优结果中的最大适应度值,最小适应度值和平均适应度值,即姿态误差最大值、最小值与平均值的具体数据如表3 所示。
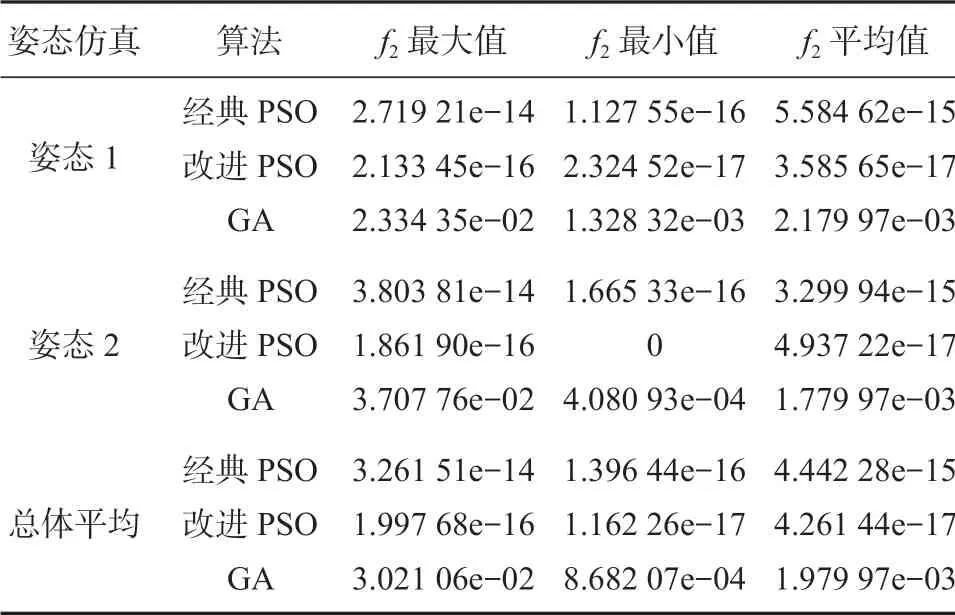
表3 3 种算法以姿态1、2 独立运行100 次的结果Table 3 Results of 100 independent runs of rotation 1 and rotation 2 under three algorithms
由表3 所示的3 种算法运行100 次的姿态误差结果,可知改进PSO 算法和经典PSO 算法的总体平均误差值分别为4.261 44e-17 与4.442 28e-15,而遗传算法的总体平均误差值为1.979 97e-03。这一结果表明,经典PSO 算法和改进PSO 算法的求解精度要优于遗传算法的,且改进PSO 算法的平均收敛精度比经典PSO 算法的更高。改进PSO 算法的总体平均最小误差为1.162 26e-17,经典PSO 算法的总体平均最小误差值为1.396 44e-16,遗传算法的总体平均最小误差值为8.682 07e-04。改进PSO 算法和经典PSO 算法的总体平均最大误差值分别为1.997 68e-16与3.261 51e-14,遗传算法的总体平均最大误差值为3.021 06e-02。由此可得,利用改进PSO 算法进行机器人逆运动学求解时,改进PSO 算法的稳定性高于经典PSO 算法的,且远高于遗传算法的。以上结果表明:改进PSO 算法在寻优精度上有了提升,且最小误差可达到0,比经典PSO 算法的求解精度都有很大优势。改进PSO 算法在寻优稳定性和寻优精度上都比经典PSO 算法有了提升,且与遗传算法对比,求解精度和稳定性上优势明显。同时,也进一步证明了改进PSO 算法的可行性。
6 结语
针对经典PSO 算法多次仿真实验中存在的不稳定问题、局部最优和种群单一的问题,提出了一种改进的PSO 算法。并以REBot-V-6R 机器人为例,首先利用螺旋理论建立了机器人的正运动学模型,将机器人的逆运动学求解问题转换为改进PSO 算法的寻优问题;并对机器人的位置误差、姿态误差分别进行仿真,验证了改进PSO 算法在求逆运动学解中的可行性。仿真实验结果表明,所提出的改进PSO 算法在满足精度要求的前提下,不仅能避免易陷入局部最优解,而且稳定性增强,收敛精度显著提高,系统鲁棒性强。

