车-温度荷载耦合作用下悬索桥钢桥面板疲劳寿命评估

张海萍，刘 扬，罗 媛，陈 斌

0 引言

正交异性板钢箱梁作为大跨度悬索桥和斜拉桥最普遍的一种结构形式[1]，其结构疲劳开裂的问题较为凸显。结构所受疲劳荷载的形式非常复杂，包括车辆荷载、温度荷载、环境介质侵蚀和地震作用等[2]。钢箱梁的喷漆工艺较为成熟，受外界腐蚀介质影响较小，一般内陆地区桥梁可以忽略环境腐蚀介质的影响[3]。地震荷载属于偶然荷载一般也可以不考虑其对结构的疲劳损伤累积。车辆和温度荷载作为结构所受到最具代表性的疲劳荷载形式，两者对结构造成的疲劳损伤不只是简单的“1+1”叠加，而是具有耦合放大的效果[4-5]。

温度对结构疲劳损伤累积作用的影响可细分为对细节点疲劳应力幅值的放大和应力循环次数的增多。我国既大跨度悬索桥的桥面铺装层主要采用沥青混凝土材料。沥青混凝土材料具有温度敏感性特征，其刚度同样具有典型的季节性特征，沥青混凝土铺装层传递扩散车辆轮轴荷载的能力随刚度的改变而发生变化。文献[6]对比了夏季与冬季某悬索桥主梁U 肋-顶板细节损伤值，在车流荷载相当的情形下，钢桥面板细节在夏季的疲劳损伤累计明显大于冬季。环境温度使得数值小的疲劳应力进入疲劳应力“门槛”值内，从而增加了可计入应力幅次数。同时主梁结构温度梯度作用会增加总疲劳应力循环的次数[7]。我国公路桥涵规范没有针对扁平钢箱梁结构形式的温度梯度模型。日照辐射下扁平钢箱梁横桥向和竖向温度梯度同样显著。同时，钢箱梁温度荷载效应与车辆荷载效应水平相当，甚至高于车辆荷载效应。在疲劳寿命分析中须考虑温度效应的叠加[8]。

本文基于南溪长江大桥WIM（weight-in-motion）系统和温度监测系统监测数据，分别建立标准疲劳车辆荷载模型和铺装层温度概率模型。计算钢箱梁温度梯度作用下焊接细节点应力水平。在ANSYS 平台计算车辆-温度荷载耦合作用下正交异性板焊接节点的疲劳应力效应，讨论车辆-温度荷载耦合作用对焊接点的疲劳寿命的影响。

1 工程背景

南溪长江大桥悬索桥作为中国西南地区最大主跨的悬索桥，是宜宾到泸州高速路上跨越长江的控制性工程大桥，其主跨跨径为820 m（见图1）。

图1 南溪长江大桥立面图Fig.1 Nanxi Yangtze River suspension bridge

在桥梁结构泸州岸安置WIM 系统，悬索桥的跨中位置安装了主梁结构、环境和铺装层温度传感器，传感器采样频率为5 Hz。行车道两车轮加载位置所对应的U 肋-顶板焊接点和U 肋-U 肋焊接点分别埋设振弦式应变传感器，采样的频率为50 Hz（见图2，图中单位为cm）。

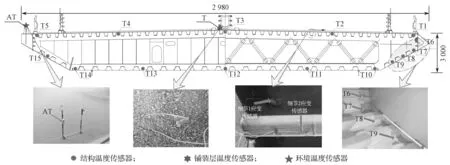
图2 温度与应变传感器布置截面图Fig.2 Layout map of the temperature and strain sensors

2 基于WIM 的标准疲劳车辆模型

2.1 车重概率模型

车辆荷载母样本监测数据包含不同车型和车辆货载率，监测的车辆荷载母样本监测数据中包含有多类子样本点。车辆荷载概率模型可以用高斯混合分布描述[9]，车重荷载的概率表达式为

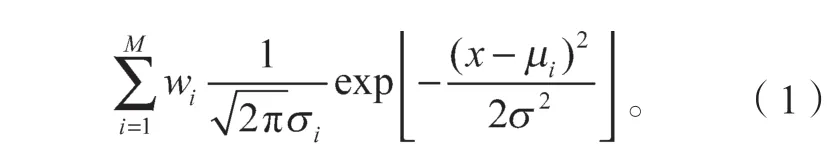
式中：μi为车质量的均值；为方差；wi为权重；矩阵参数θ包含wi、μi和3 类变量；x为车质量统计样本值。

课题组在文献[1]中将车辆按照轮轴数进行车型分类，将采集样本车辆分为C2、C3（1）、C3（2）、C4、C5 和C6 共6 类典型车辆模型，表1 给出了南溪长江大桥典型车辆的多峰概率分布模型参数[2]。

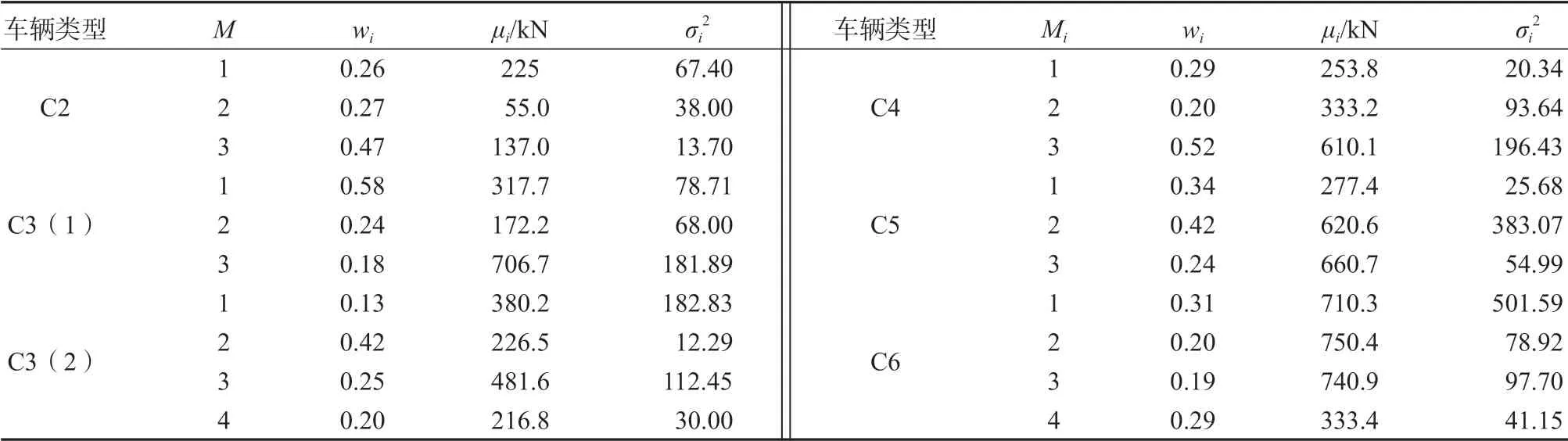
表1 6 类典型车辆的高斯混合模型参数估计值Table 1 GMM parameter evaluation of 6 types of vehicle weight

2.2 标准疲劳车辆模型

根据Miner 等效线性损伤定理[10]，疲劳车辆的等效车重可依据以下表达式得到：

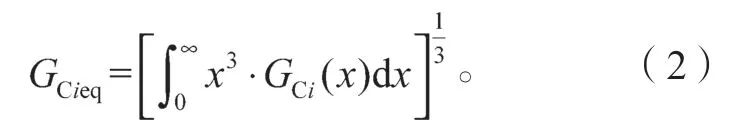
采用式（2）计算得到标准疲劳车辆车重，需依据车重与轴重之间的关系式计算标准疲劳车辆的轴重模型。因同类车型的轴距和重心具有不确定性，难以采用单一力学模型去构建车重与轴重之间的关系式。Wang T.等[11]认为同一类型车重和轴重具有很强的线性相关性。课题组基于WIM 的海量车重与轴重的监测数据，对6 类车型的车重与轴重实测数据进行线性回归，线性回归表达式为

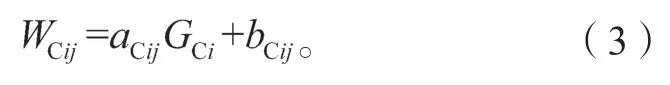
式中：WCij为典型车辆Ci的第j轴轴重；aCij为斜率参数；bCij为位置参数。

对于C3（1）车型，轮轴1 和轮轴2 具有相同的刚度，且轮轴1 和轮轴2 属于连轴，挂车的支点加载位置在连轴的中心，可知轴1 和轴2 的荷载值相等。同理，C3（2）的轴2 和轴3 为连轴；C4 的轴3 和轴4 为连轴；C5 的轴3、轴4 和轴5 为连轴；C6 的轴2 和3 轴为连轴，轴4、轴5 和轴6 为连轴。基于车辆荷载统计数据，采用线性回归的方法得到6典型车型车重与轴重的线性表达式（见图3）。由于WIM 系统很难完成对车辆轴距的监测。本文参照文献[12]中的轴距数据。基于车重、轴重和轴距的统计数据，计算得到6 类标准车辆疲劳荷载模型（见附表1）。

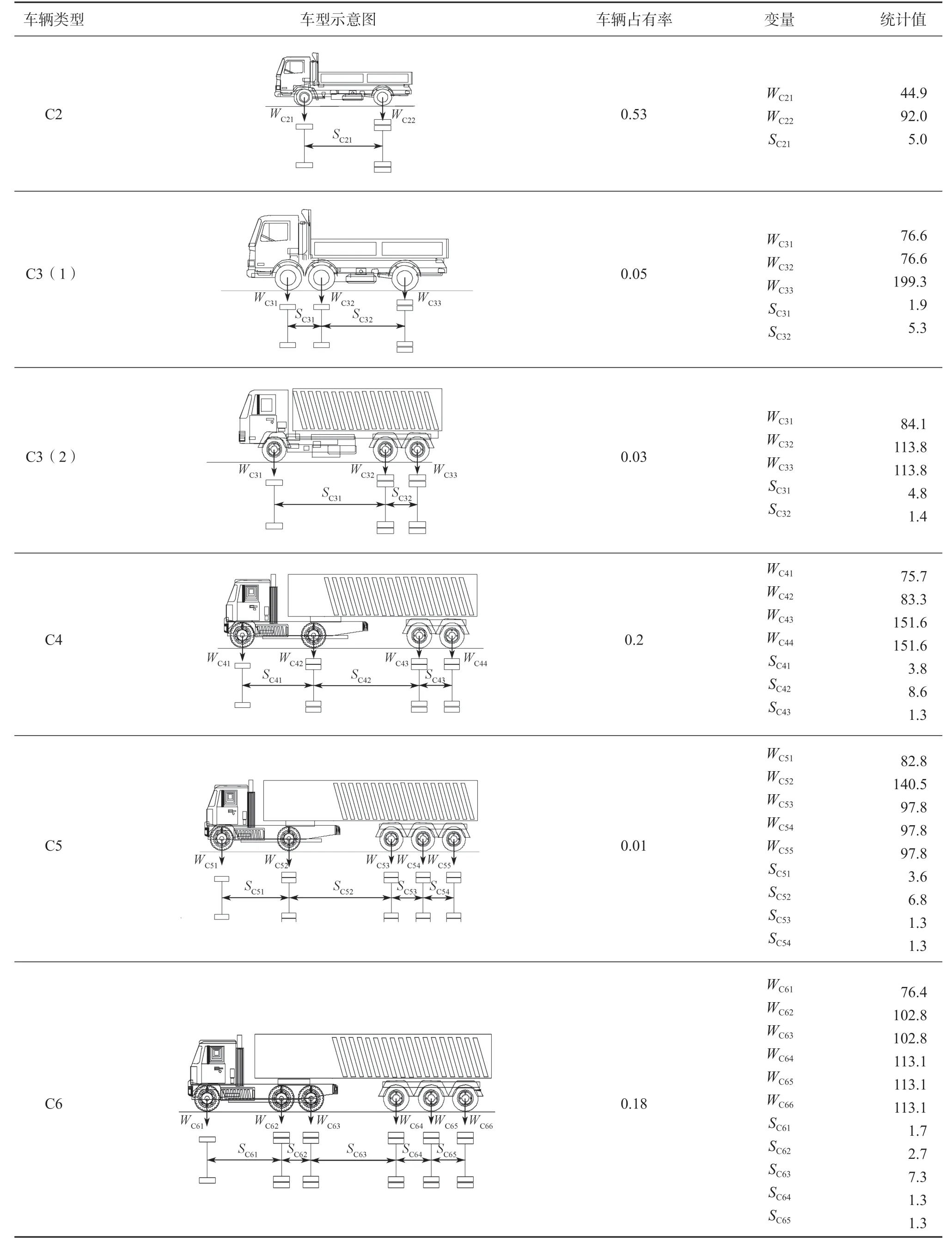
附表1 6 类标准车辆的疲劳荷载模型Table 1 Fatigue-loaded vehicle models

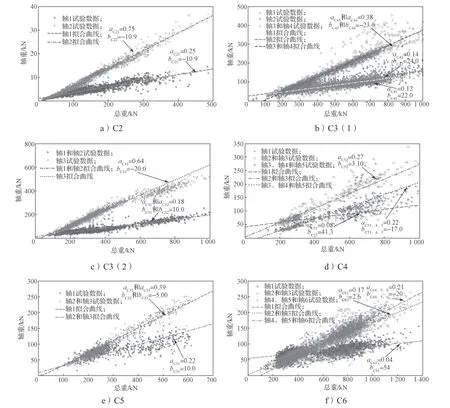
图3 6 类典型车型车重与轴重的线性回归结果Fig.3 6 types of vehicle axle weight linear regression model

3 车-温度荷载耦合作用下钢桥面板细节疲劳应力分析

3.1 有限元模型的建立

为实现车辆荷载与疲劳应力效应之间的转化，在ANSYS 平台建立正交异性钢箱梁结构的局部模型。主要研究对象为U 肋-顶板焊接和U 肋-U 肋对接两类细节。车辆轮轴局部荷载对横向的其他车道细节点产生的应力很小，对其他车道疲劳损伤的累计可忽略不计。为提高计算效率，建立半幅钢箱梁有限元模型，该局部模型采用solid45 单元和shell63 单元，分别模拟正交异性钢箱梁结构的沥青铺装层和正交异性板材料。对沥青铺装层、顶板、底板和U 肋采用矩形进行网格划分，用三角形对横隔板进行单元网格划分。

本文假设主梁结构在承受车辆荷载时不发生滑动位移和扭转，对局部有限元模型的边界节点的6个自由度进行限制。沥青混凝土铺装层的厚度为70 mm，当铺装层温度为20 ℃时，沥青混凝土的弹性模量和泊松比分别为6 147 MPa 和0.2。U 肋的顶板、腹板和底板厚度分别取14, 8, 10 mm。U 肋的弹性模量和泊松比分别为210 GPa 和0.3，主梁的局部有限元模型见图4，图中单位为mm。

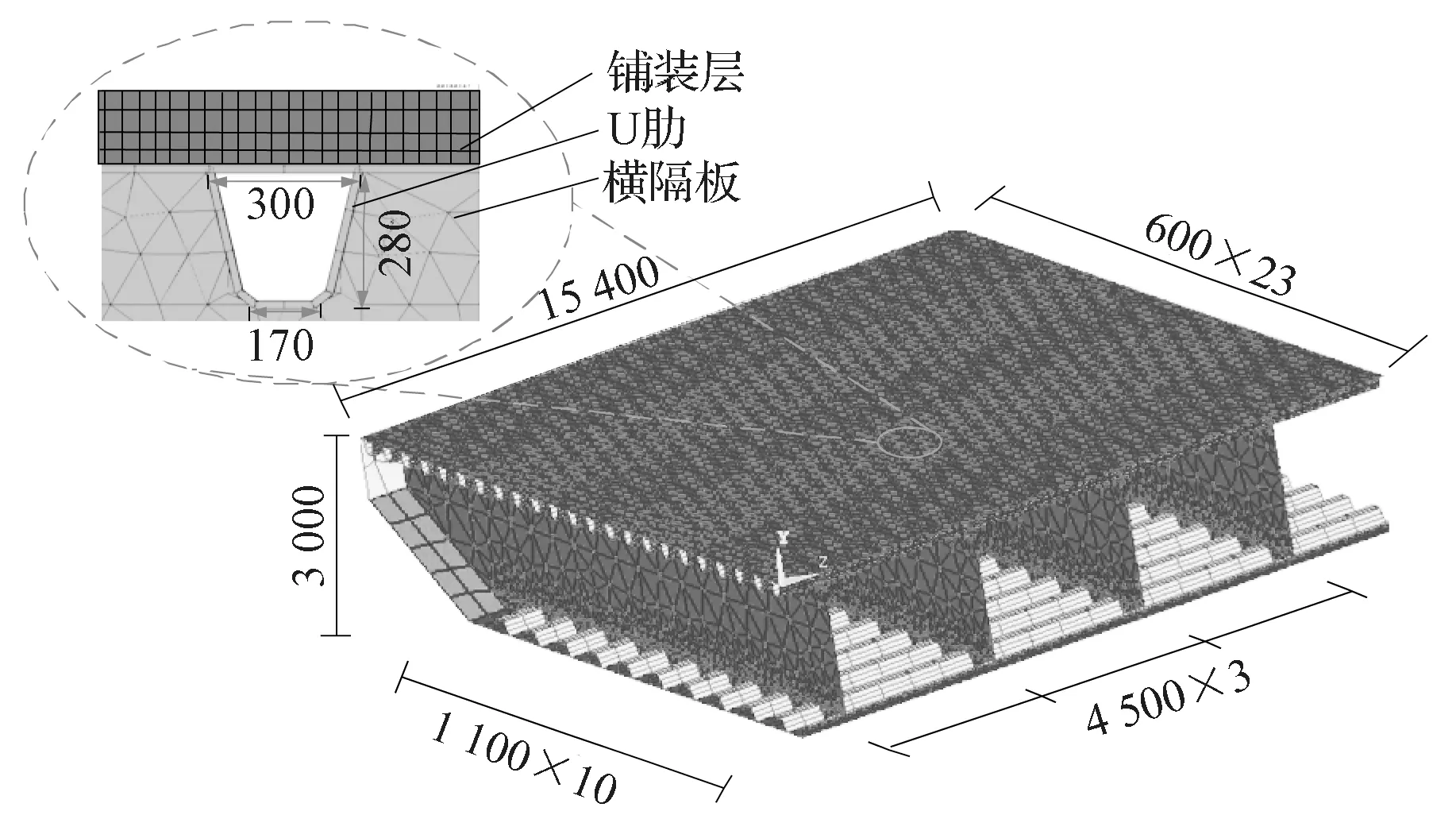
图4 正交异性钢箱梁局部有限元模型Fig.4 Local finite element of OSD

沥青混凝土铺装层对温度敏感性较强，温度与沥青混凝土材料的弹性模量呈负相关性。温度越高，材料的弹性模量越小。当环境温度升高时，沥青混凝土铺装层传递荷载的能力减弱。图5 为不同温度环境铺装层的扩散传递荷载示意图。由图5 可知，在低温环境下，沥青混凝土铺装层变形小、刚度大，扩展传递荷载能力强。当轮轴荷载传递到钢桥面板的顶板时，荷载的局部效应变小。在高温环境下，沥青混凝土受轮轴荷载作用下的变形较大，扩散传递荷载的能力相对较弱。细节点在受相同大小荷载的情况下，细节点应力效应相对较大。不可忽略瞬态分析过程中沥青混凝土温度对疲劳应力效应的影响。

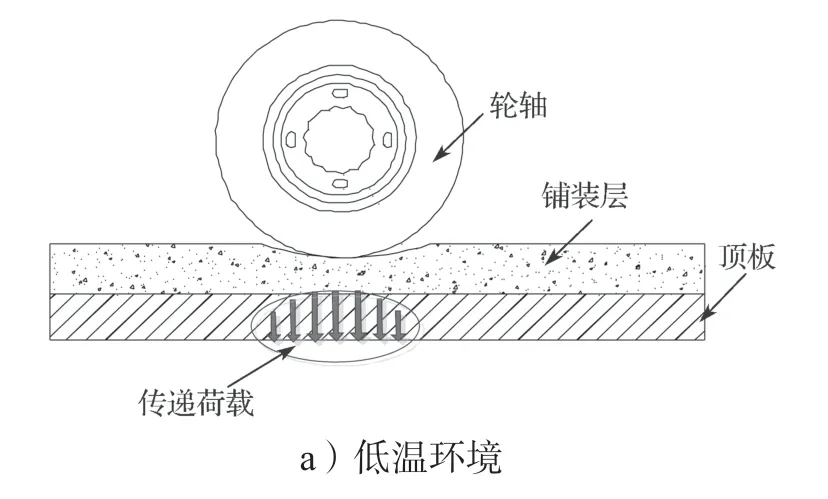
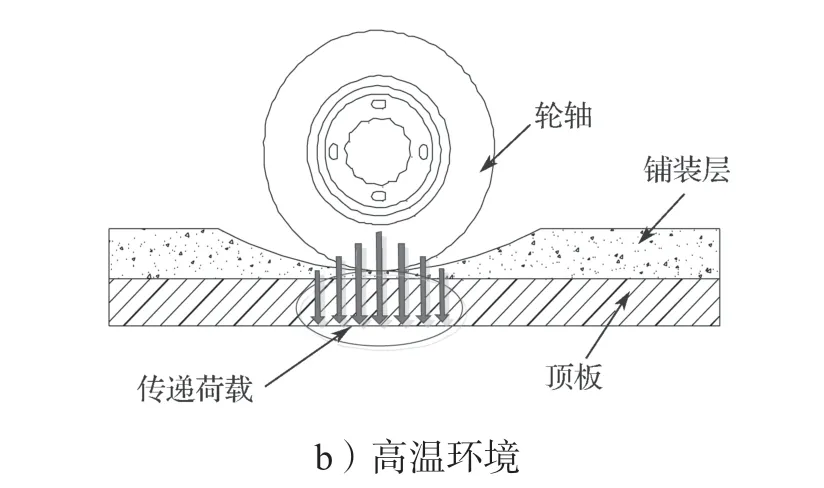
图5 不同温度环境铺装层的扩散传递荷载示意图Fig.5 Schematic diagram of diffusion transfer load of pavement at different temperatures

文献[13]给出了如下沥青混凝土的温度与弹性模量的对应关系式：

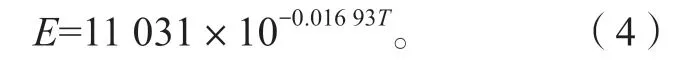
式中：E为沥青混凝土的弹性模量；T为沥青混凝土的温度，沥青混凝土的温度通过埋设在铺装层的传感器进行实时监测。

3.2 瞬态分析

采用瞬态分析来模拟车辆过桥。加载荷载采用车轮截面大小的均匀力模拟轮轴荷载。瞬态分析的计算步骤为：首先确定车辆的到达时间。以第一辆疲劳车辆模型前轮轴作用在结构的第一个节点作为开始时间点。后续车队按照车速与车距的关系式，计算到达作用节点的时间。然后基于行车车速、轴距和有限元网格的划分长度计算节点加载时间。最后删除前一个荷载加载步骤。依次循环3 个计算步骤，来模拟多车上桥的瞬态分析过程。

3.3 模型验证

对比有限元计算结果与应变实测数据来验证瞬态分析的应力时程曲线精准性是否满足要求。监测2014年4月3日16 时6 分一辆C3 型货车的荷载信息和应变时程数据。该车的轴距分别为4.50, 1.35 m，轴重分别为58, 83, 83 kN，行车时速为72 km/h。沥青混凝土铺装层的实时温度为22 ℃（见图6）。

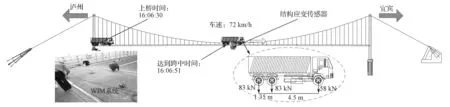
图6 实测车辆荷载过桥图Fig.6 Diagram of vehicle load crossing bridge under measurement

图7 为细节应力有限元计算和实测数据对比图。

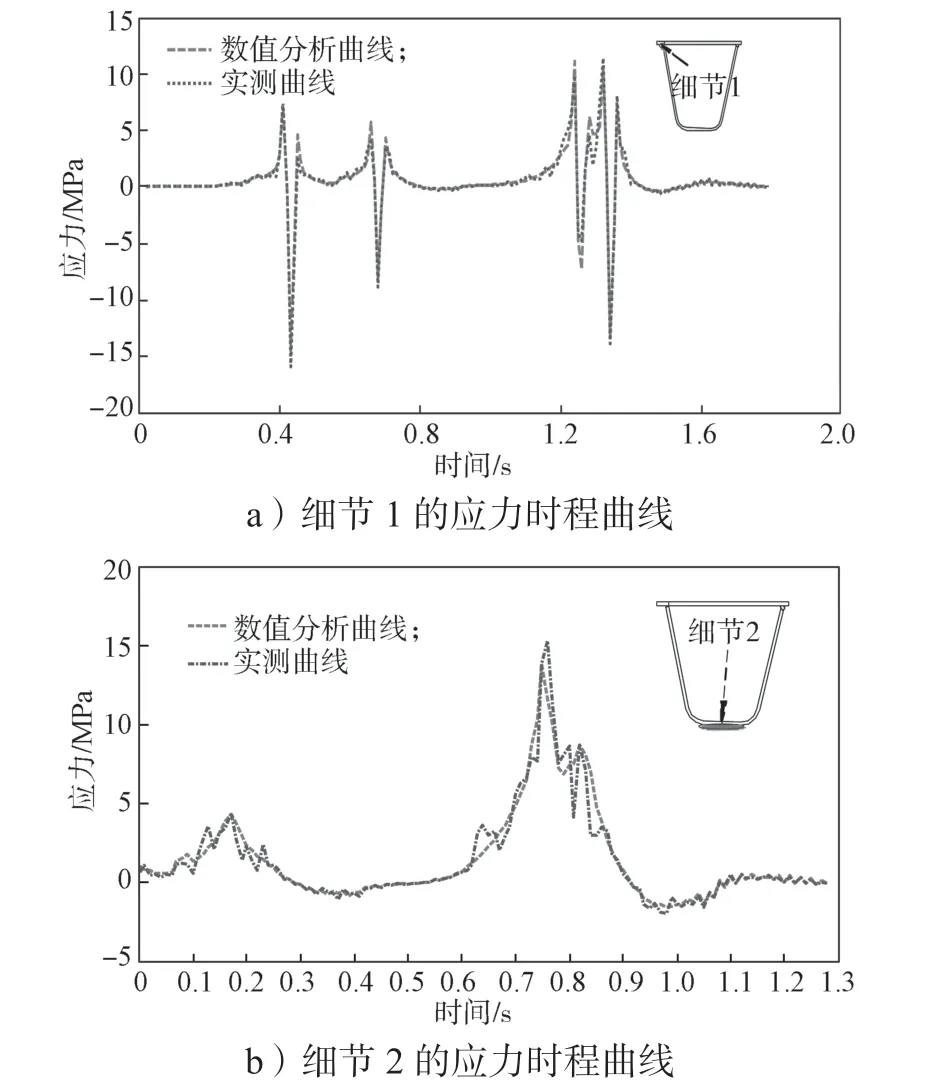
图7 细节应力有限元计算和实测数据对比图Fig .7 Comparison diagram of detail stress finite element calculation and measured stress data

由图7 可知，有限元计算和实测结果基本吻合，实测应力时程曲线相对“毛刺”较多。外界干扰信号和车-桥耦合振动作用是造成“毛刺”的主要原因。

以C4 车型为代表，分析典型车辆作用下在不同的沥青材料温度的应力时程曲线，如图8 所示。

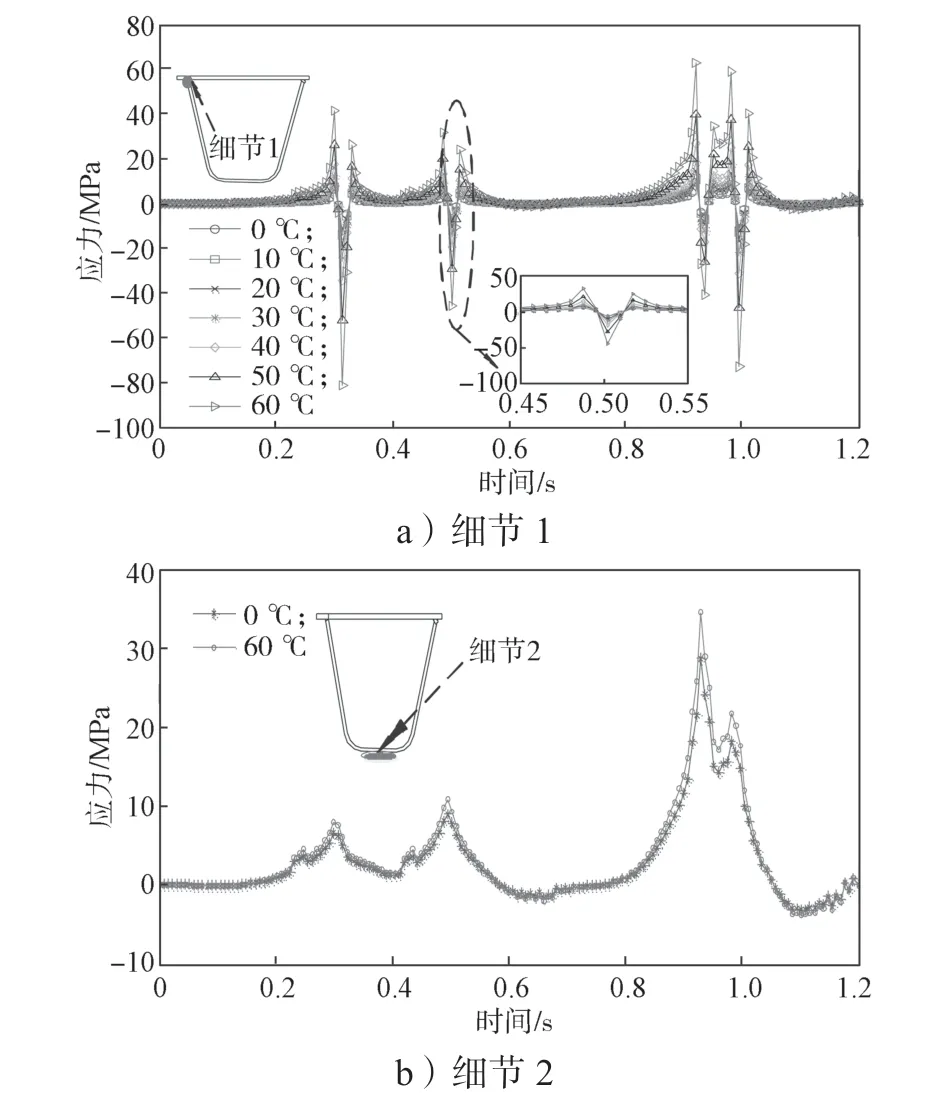
图8 不同温度下C4 作用两类细节的应力时程曲线Fig.8 Stress time-history curves for welded details under C4 loading at different temperatures

由图8a 可知，铺装层温度在0℃时，细节1 的最大拉应力为15.3 MPa，而当铺装层温度为60 ℃时，细节1 的最大拉应力值为60 MPa，两者最大拉应力比值达3.92 倍。由图8b 可知，铺装层温度在0 ℃时，细节2 的最大拉应力为17.5 MPa，当铺装层温度为60 ℃时，细节2 的最大拉应力值为25.9 MPa，两者最大拉应力比值仅为1.48 倍。造成两类细节点应力对温度敏感性具有较大差异的原因，是细节点距离沥青铺装层的距离大小不同。细节点距离铺装层近，受铺装层扩展荷载能力的影响较大。

4 正交异性板温度梯度疲劳应力谱

4.1 横桥向温差时变曲线

正交异性板在正温度梯度和负温度梯度作用下的应力场有本质的区别[14]。需要将正温差与负温差分开进行讨论。图9 给出了T2-1和T2-3两组变量的1 a 内时变模拟曲线。用分割线对模拟数据进行分割。

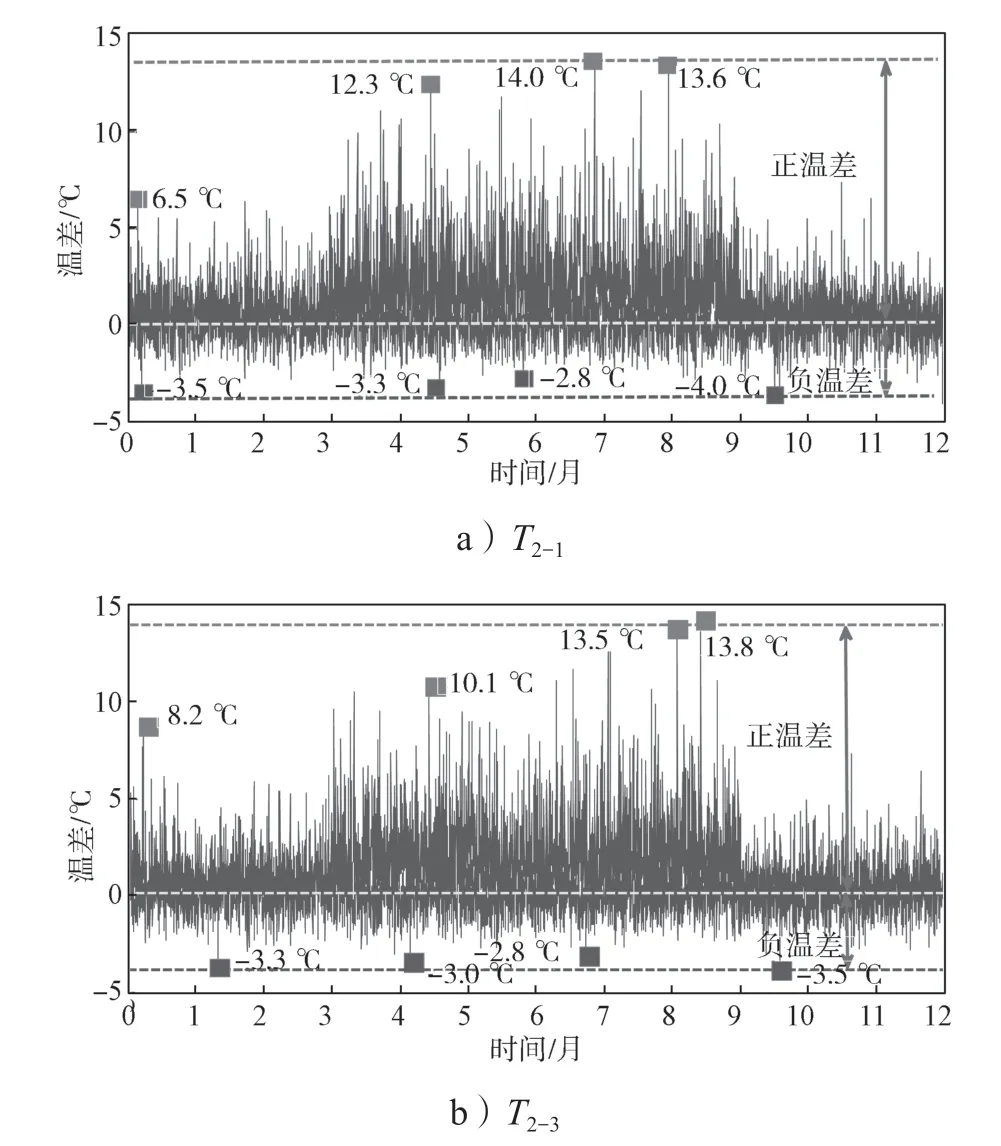
图9 正交异性板横向温度梯度变化曲线Fig.9 Measured transverse temperature gradient curves of OSD

由图9a 可知，夏季的钢箱梁的整体横向温差明显要高于其他季节。对于T2-1，4 个季节的横向正温温差极值分别为12.3, 14.0, 13.6, 6.5℃；负温差在4个季节变化较小，负温差极值分别为-3.5, -3.3, -2.8,4.0 ℃。由图9b 可知，T2-3在4 个季节的横向正温差极值分别为10.1, 13.5, 13.8, 8.2 ℃。最小负温差值为-3.5℃。

4.2 温度梯度应力计算

在ANSYS 有限元平台计算温度梯度的效应有两种方法：第一种方法是在不知结构温度场分布的情况下，基于热传导的基本原理，在有限元中输入日辐射强度参数、辐射角度参数以及其他的边界参数先求解结构的温度场，然后计算结构的应力效应。第二种计算方法是已测得结构的温度场数据的情况下，可以将温度荷载模拟成体荷载分别对shell63 壳单元的8 个节点进行温度输入。为校验计算模型的精准性，输入与文献[15]相同的温度梯度进行对比计算。温度梯度有限元加载模型如图10 所示。在横向温差作用下，结构最大的拉应力为28 MPa（文献[15]为24 MPa），应力分布形式相似（见图10b）。表明计算模型的准确性。

图10 顶板横向温度梯度荷载模型和应力效应Fig.10 Lateral temperature gradient load model with its stress effect

根据温差统计数据与有限元计算分析，采用雨流计数法得到的温度梯度疲劳应力谱，如图11 所示。由图中可知，钢箱梁横向温差作用下关注点年温差应力谱的平均疲劳应力幅值为7.8 MPa，最大应力幅值为19.5 MPa。横隔板竖向温差作用下，关注点平均疲劳应力幅值为12.1 MPa，最大应力幅值为28.3 MPa。横隔板竖向温差效应明显大于顶板的横向温差效应。值得说明的是，本文将关注点温差应力分析分割为横向顶板温差效应和横隔板竖向温差效应两类计算。事实上，关注点温差疲劳应力谱为两种温差的耦合作用下的应力时程曲线，实际疲劳应力幅值应明显高于本文计算结果。

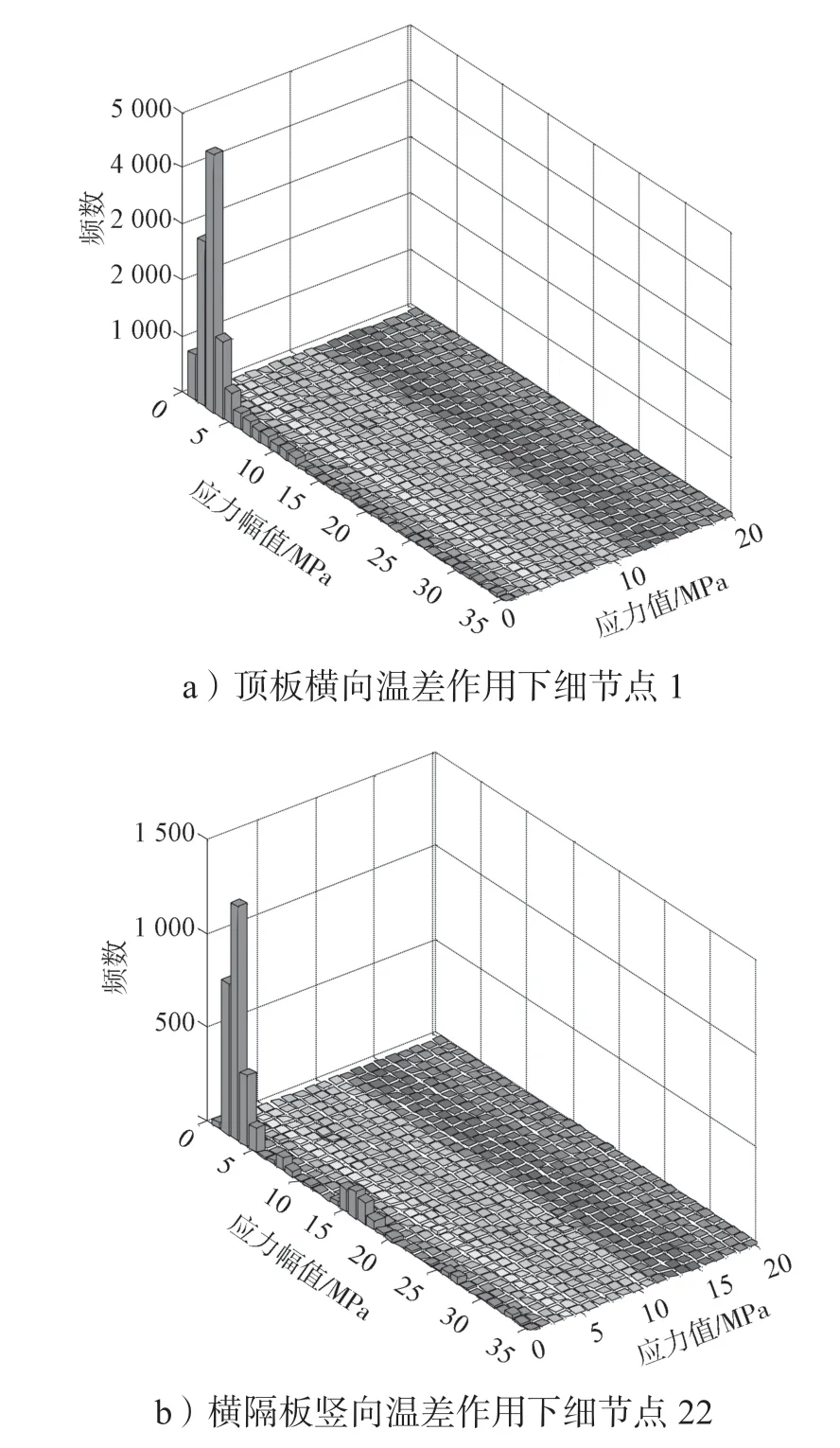
图11 温度梯度作用下两类细节疲劳应力谱Fig.11 Fatigue stress spectrum of two kinds of details under temperature difference loading

5 疲劳损伤分析

欧洲Eurocode 规范给出了大多数正交异性板的焊接细节的疲劳强度参考曲线，能够满足工程应用要求[16]。查规范可知，将U 肋-顶板焊接细节类型为50，U 肋对接焊接细节类型为71。欧洲Eurocode 规范的疲劳强度曲线表达式进一步简化成以下形式：

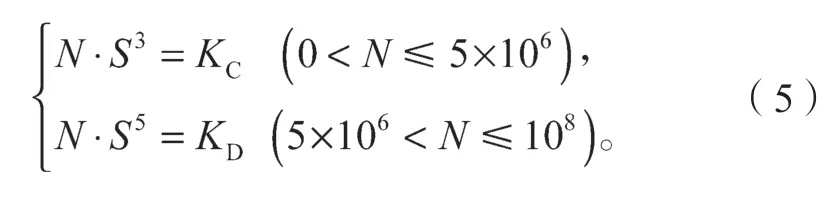
式（5）中：S为疲劳应力幅；N为与S对应的疲劳寿命；KC和KD分别为低周期和高周期疲劳强度系数，KC和KD的表达式如下：

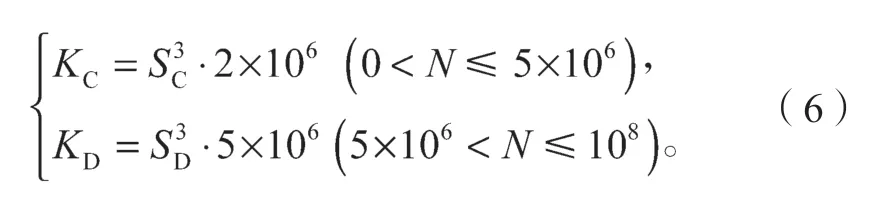
本文研究对细节类型按照Eurocode 规范为类型H 和M，依据Eurocode 规范，U 肋-顶板细节疲劳强度系数KC和KD分别取7.16×1011和1.90×1015。U 肋-U 肋对接细节KC和KD分别取2.50×1011和3.17×1015。

假设结构细节点经历了总次数为n的循环应力S，其中S＞SD的应力循环数为ni个，对应的应力变量为Si，S≤SD的应力循环数为nj个，对应的应力变量为Sj。SD为高周期疲劳和低周期疲劳应力的界限值。依据Miner 线性损伤准则可推断结构细节疲劳损伤计算表达式为

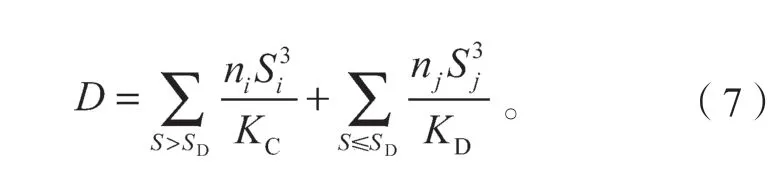
式（7）计算变应力幅值作用下细节的疲劳损伤，在实际工程中，往往应力幅有较多的等级，计算疲劳损伤的计算量大，需要进行一步简化计算步骤，假设有n个常幅应力Seq对结构造成的疲劳损伤与式（7）相等，当常幅应力Seq＜SD时，则有：

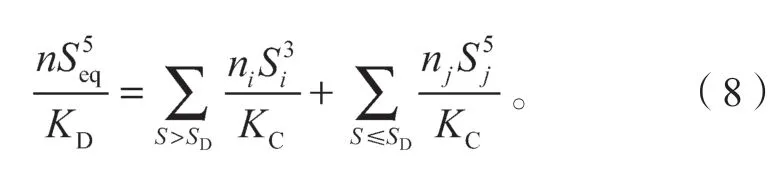
可得到Seq的表达式为

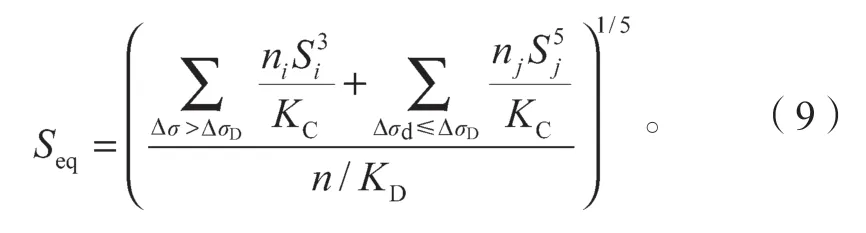
当常幅应力Seq≥SD时，则Seq的表达式为

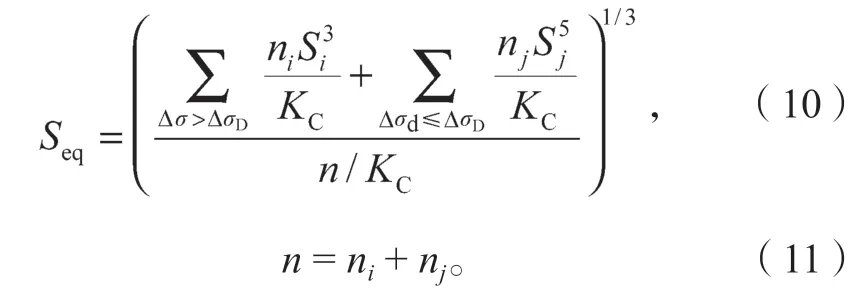
车辆与温度耦合作用以及温度梯度作用对细节点的应力峰值影响较大。在对正交异性板结构细节疲劳损伤计算时，需要把温度参数考虑在内。在ANSYS 有限元平台分别计算6 种标准车辆作用下，铺装层温度与细节等效应力幅可以采用如下线性回归方程表示[17]：

式中cj和dj为线性方程式的系数。

6 类典型车型作用下细节的疲劳应力幅具体参数见表2。

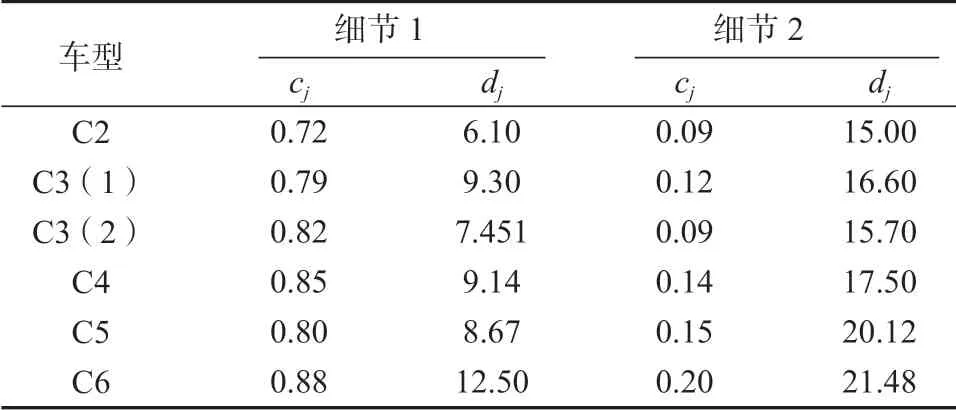
表2 典型疲劳标准车辆作用下细节点应力与温度线性回归关系式参数Table 2 Parameters of linear equation between temperature with vehicle loads

基于WIM 系统和温度传感器监测系统的车辆荷载、沥青铺装层温度和主梁温度监测数据，在有限元平台将疲劳荷载数据转换为细节点应力数据，并通过雨流计数法对应力输出数据进行处理，得到正交异性钢箱梁结构两类细节点的日应力循环数Nd和日等效应力幅Seq，如图12 所示。

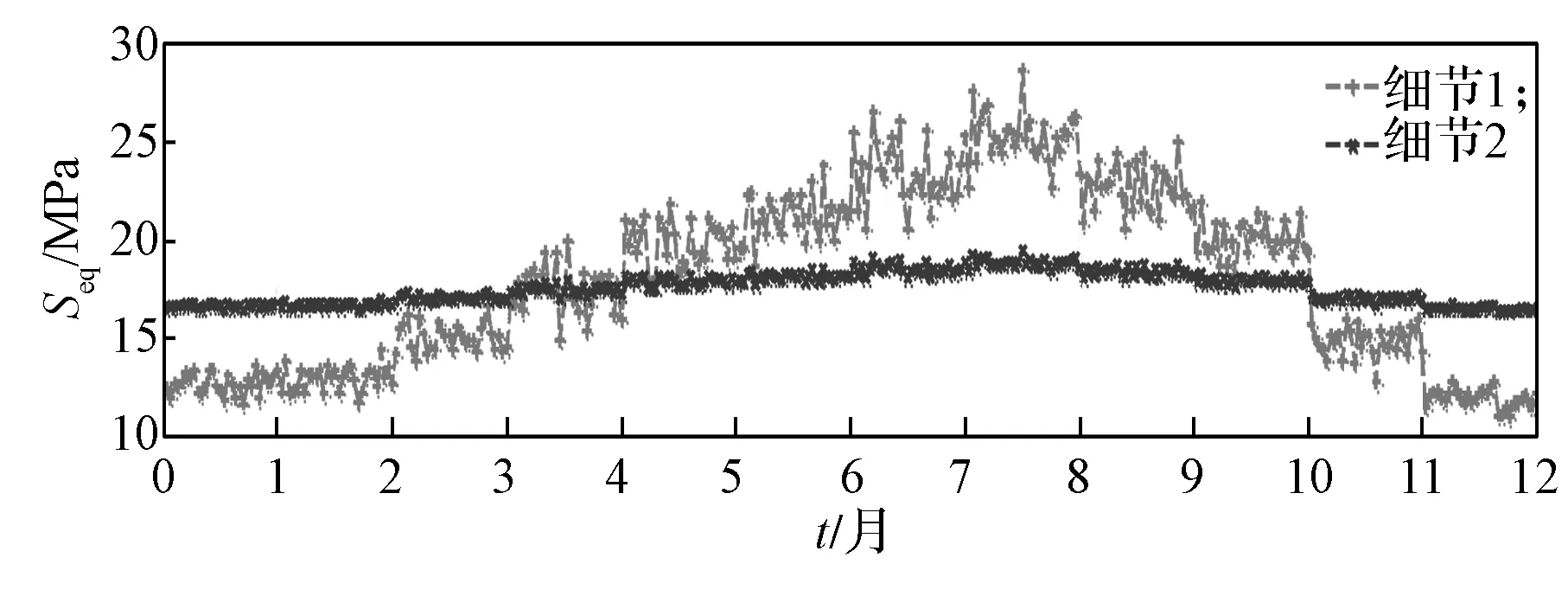
图12 两类细节日等效应力幅时变曲线Fig.12 Daily equivalent stress range curves for two details

由图12 可知，细节1 的等效应力值变化较大，等效应力幅在8月份最大，8月份的平均应力幅值是12月份的1.92 倍。造成夏季钢箱梁焊接细节等效应力幅值明显大于其他季节的原因是夏季平均温度高于其他季节，沥青混凝土的弹性模量变小，传递和分散局部荷载的能力下降，使得与沥青混凝土面层距离较近的细节点1 的应力变大。细节2 处于U 肋底部，距离铺装层相对较远，局部荷载通过顶板传递到U肋底部的过程中，U肋通过弯曲变形承受荷载，细节2 的受局部荷载影响较小， 故其应力幅值变化范围较小。

图13 所示为两类细节日等效应力幅循环数时变曲线图。

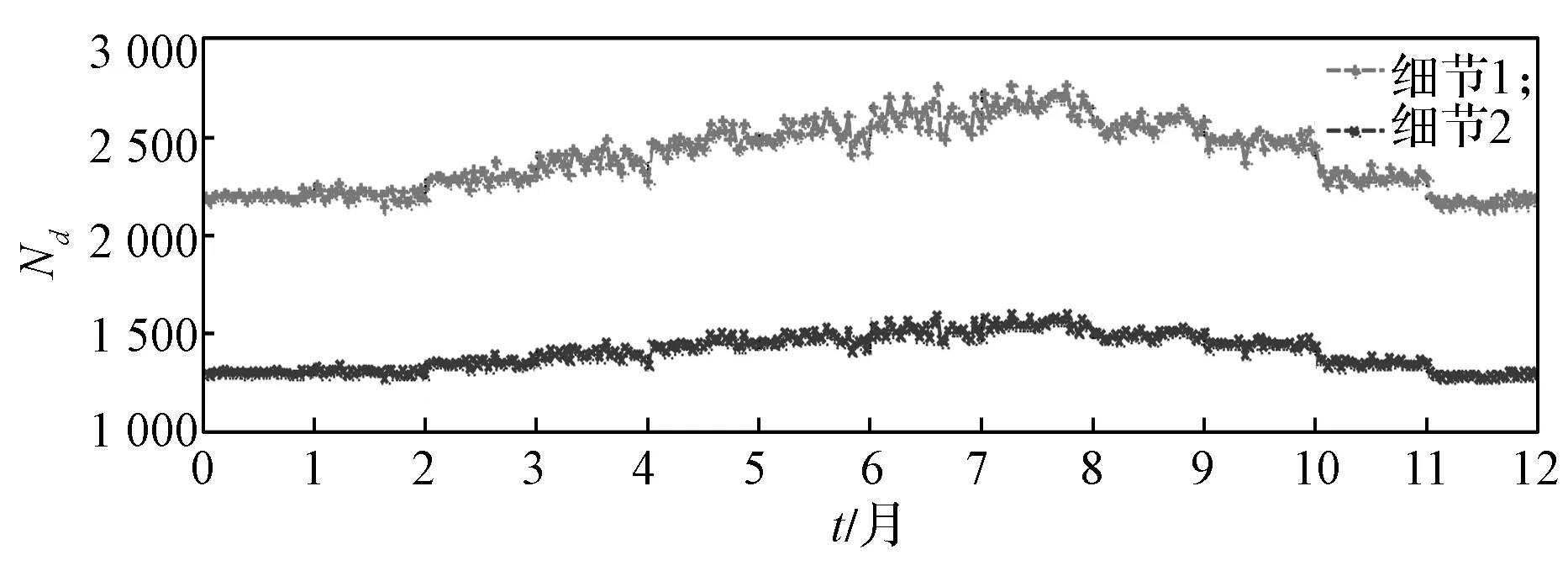
图13 两类细节点日等效应力幅循环数时变曲线Fig.13 Daily stress range number curves for two details

由图13 可知，等效应力幅循环次数受季节影响相对较小，夏季Nd的平均值仍大于其他季节。根据WIM 系统对交通统计数据可知，日交通量相对稳定，夏季的车流量与其他季节相当，故交通量的变化不是影响Nd值的关键因素。沥青面层的温度仍是决定Nd的关键变量。铺装层温度的升高使得细节1 的疲劳荷载效应变大，大量的低于Eurocode 规范的疲劳极限应力门槛的应力幅“越界”到“门槛”内，从而增加了疲劳应力幅值循环数。

表3 列出了12 个月份正交异性板两类细节点的日应力幅、日应力循环次数和疲劳损伤均值。

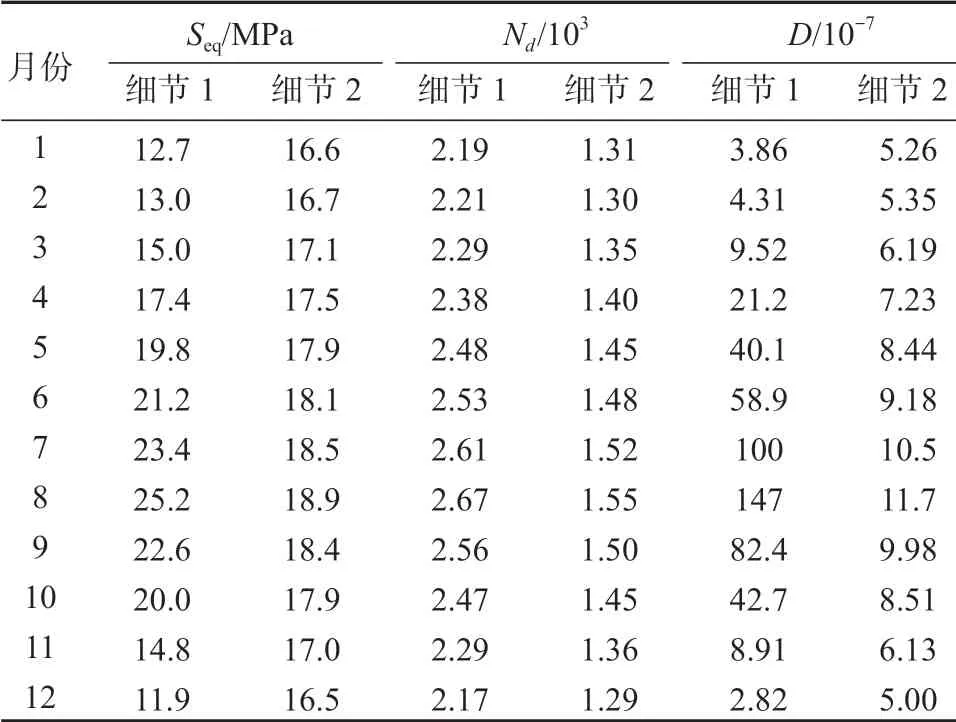
表3 两类细节月Seq、Nd 和D 均值统计表Table 3 Monthly mean value data of Seq, Nd and D for two details

图14 为两类细节的日疲劳损伤对比图。

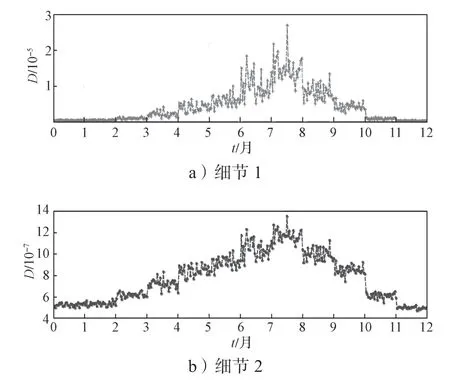
图14 两类细节点日疲劳损伤时变曲线Fig.14 Daily fatigue damage curves for two details

对于细节1 的日最大疲劳损伤值与最小损伤值相差了近两个数量级。应力幅值的增大会使得材料的疲劳损伤呈现指数倍数增长[18]，等效应力幅值的不同是造成日疲劳损伤相差甚大的主要原因。

6 疲劳寿命预测

6.1 温度对疲劳寿命的影响

假设该桥的车流量每年保持不变，第d 天的日应力循环数为Nd，则该桥梁服役ma 后，两类细节的疲劳损伤值为

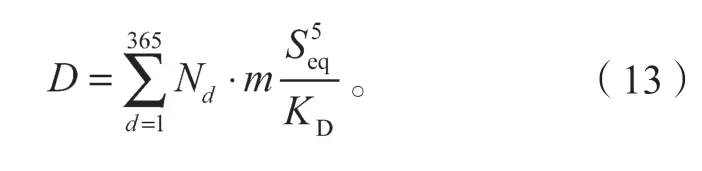
当D=1 时，细节点疲劳失效。

假设年交通荷载量和环境温度总值不变，依据表4 和式（13），对两类细节进行疲劳损伤预测。图15给出了两类细节的疲劳损伤发展曲线。

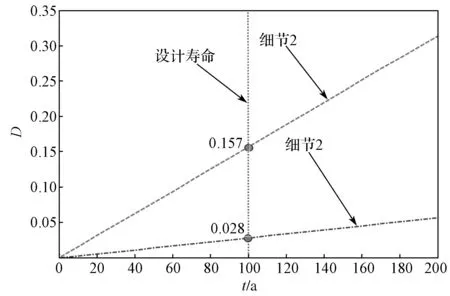
图15 两类细节疲劳损伤发展曲线Fig.15 Fatigue damage curve line of two details

从图15 可以看出，细节1 的损伤发展速率明显高于细节。两类细节在设计期内均没有发生疲劳失效，当桥梁服役100 a 时，两类细节的疲劳损伤值分别为0.157 和0.028。细节1 和细节2 的疲劳预测寿命分别为636 a 和3 521 a。

图15 中细节点疲劳损伤的线性累计是由车辆荷载、沥青温度以及钢箱梁温度梯度3 类荷载共同作用而成。各类型荷载对结构的疲劳损伤的贡献率需要进行讨论分析。现假设钢箱梁沥青混凝土铺装层的温度保持在20 ℃不变，即有限元模型中沥青混凝土铺装层的弹性模量为恒值。同时不考虑钢箱梁温度梯度疲劳荷载的作用，计算仅车辆荷载作用下钢桥面板细节点的疲劳损伤发展曲线。图16 为车辆荷载与温度对两类细节疲劳损伤贡献区域对比图。由图16a 可知，考虑与不考虑车-温度荷载耦合作用，桥梁服役100 a 后主梁细节1 疲劳损伤计算值相差5.06 倍，车辆和温度耦合作用下细节疲劳损伤的区域面积远大于车辆荷载的贡献区域，细节1 的疲劳损伤对温度敏感性校高。由图16b 可知，桥梁达到设计寿命值时，考虑与不考虑车-温度荷载耦合作用细节2 的疲劳损伤值相差1.50 倍。车辆荷载贡献区域要大于两类荷载耦合作用贡献区域，表明细节2 疲劳损伤对温度敏感性较弱。

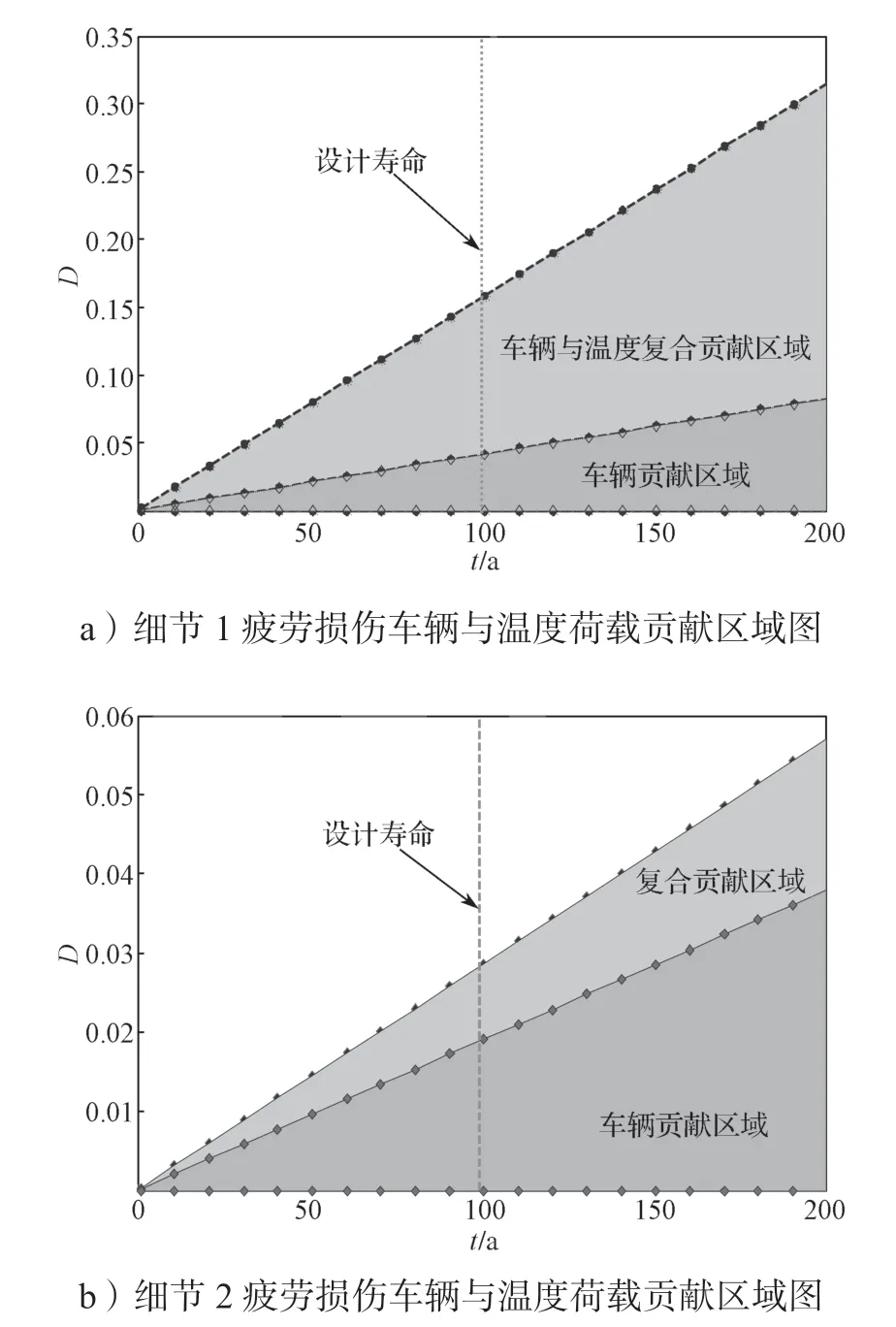
图16 两类细节疲劳损伤贡献率对比图Fig.16 Fatigue damage contribution rate of two details

6.2 交通增长率对疲劳寿命的影响

随着我国交通运输业的不断发展，车流量也会随之增长。但因桥梁宽度一定，交通量增长速度不会无限制的呈现非线性增长，本文假设每年交通量的增长是线性的，增长率系数为α，则桥梁运营ma 后，正交异性板细节疲劳损伤表达式为

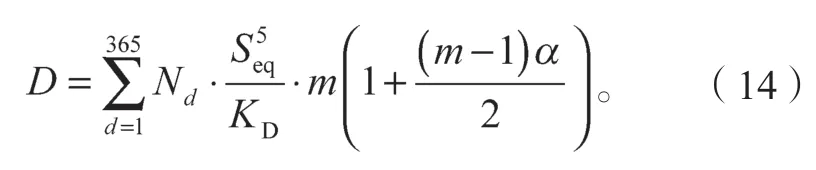
图17 给出了两类细节在不同交通增长率下疲劳损伤发展曲线。

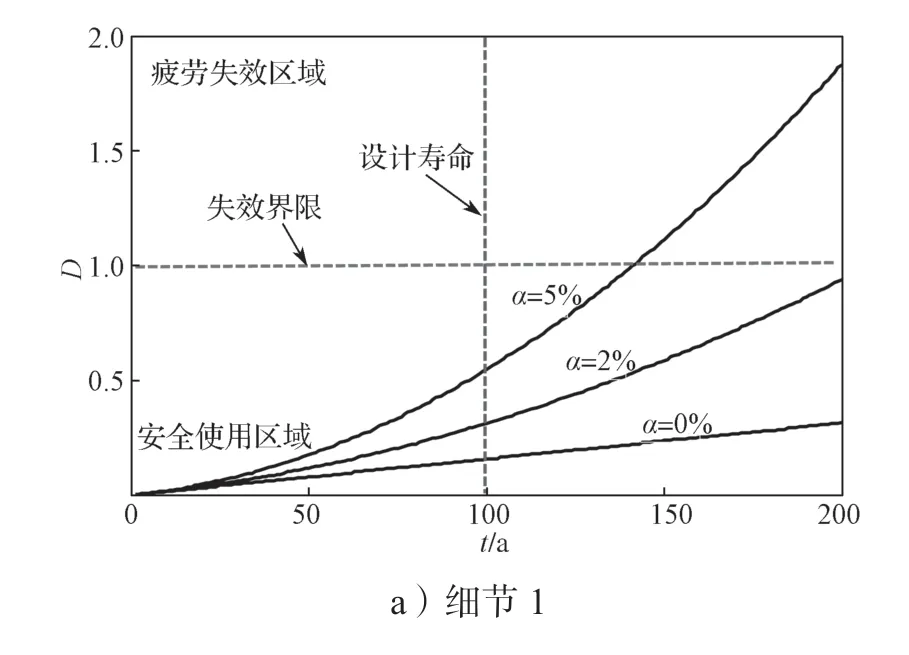
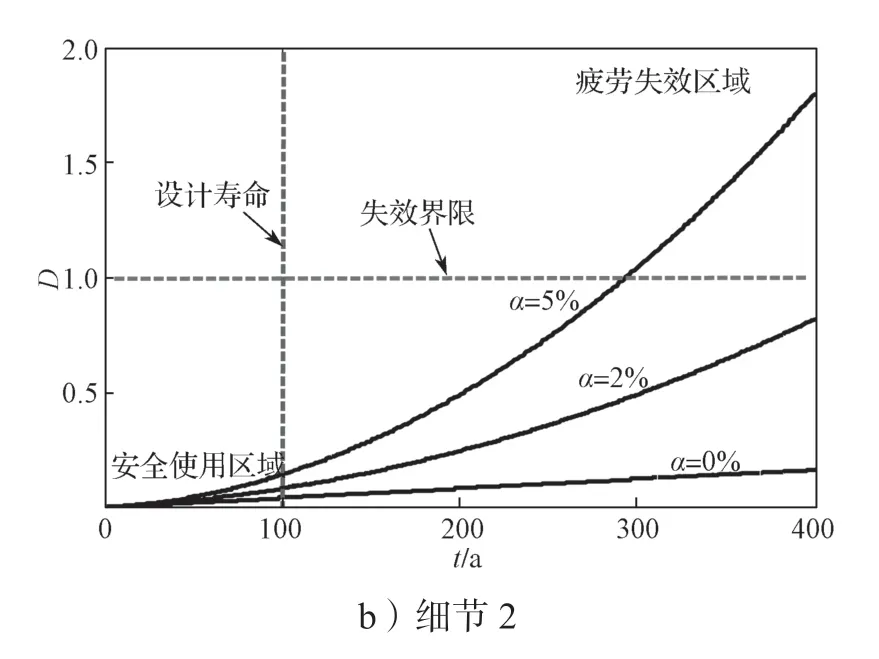
图17 不同交通增长率两类细节的疲劳损伤演化曲线Fig.17 Fatigue damage evolution curves of two kinds of details with different traffic growth rates

由图17 可知，当交通增长率为0%, 2%, 5%时，两类细节在设计使用寿命范围内均不出现疲劳失效。其中细节1 的疲劳寿命分别为636, 452, 143 a。

7 结论

本文基于南溪长江大桥健康监测系统中WIM 系统和温度传感器监测数据，建立一套考虑车辆-温度荷载耦合作用下钢桥面板焊接细节疲劳寿命评估方法，得到以下结论：

1）在车辆荷载不变的情况下，沥青铺装层温度与等效应力幅呈现线性关系式。对距离铺装层近的细节点（细节点1），车辆-温度荷载耦合放大应力效应影响明显。对于距离铺装层较远的细节点（细节点2），影响较小。

2）结构本身的温度梯度的变化产生的温度次应力大小与车辆荷载效应大小相当。对细节的疲劳损伤具有叠加累积的效果。但受限于温度梯度应力幅次数相对较小，在疲劳累计损伤中贡献小。

3）南溪长江大桥主梁钢桥面板的焊接细节疲劳损伤的主要贡献时间为夏季。在钢桥疲劳设计时，要将环境温度效应考虑在内。温度梯度疲劳荷载谱的循环次数明显较车辆荷载小，在两者耦合作用中，车辆荷载对疲劳损伤的贡献值占据主要地位。