高速多体船的解析预测控制减纵摇方法

张军， 温昊， 刘志林， 李国胜

(1.江苏大学 电气信息工程学院， 江苏 镇江 212013； 2.哈尔滨工程大学 智能科学与工程学院， 黑龙江 哈尔滨 150001)

0 引言

高速多体船使用流线型支柱将排水体积与主体部分连接起来，具有甲板面积大、航行阻力小、耐波性好、运载能力强、横向稳定性好等优点[1]。然而，在高海况航行时高速多体船的升沉和纵摇运动变化剧烈，这是因为多体船具有细长的侧体，不同航速的水动力会对水下船体产生不同程度的纵向倾覆力矩，该力矩随纵倾角的增大而增大，并且多体船的纵向恢复力矩非常小。纵摇和升沉幅度过大，容易引起失速、艏部砰击、乘员晕船等现象，严重影响适航性，因此需要采取合理的措施抑制升沉和纵摇运动幅度。目前在船体上安装T型翼和压浪板两种附体可以实现协同减摇，T型翼安装在船艏底部，可有效增加船体的附加质量和阻尼，降低高速多体船的垂向运动幅度；压浪板安装在船尾，可以实现减阻[2-3]。

高速多体船的减摇控制是根据多体船航态的改变自动调节T型翼和压浪板的攻角，增加附体的恢复力和力矩[2]，从而减少升沉和纵摇运动幅度。然而，多体船的升沉和纵摇运动之间存在强耦合，并且水动力学系数具有较强的不确定性。针对多体船耦合的垂向运动模型，文献[4]提出比例- 微分控制和传递函数解耦矩阵方法来减少升沉和纵摇运动幅度，但是解耦矩阵需要事先准确辨识多体船传递函数，否则难以做到完全解耦，鲁棒性较差。为了避免设计升沉和纵摇的解耦矩阵，文献[5]设计线性高斯二次型控制器(LQG)实现减摇，但是没有明确考虑水动力系数不确定性。为了提高减摇控制的鲁棒性，文献[6]提出模糊比例- 积分- 微分(PID)减摇控制，但是模糊规则选择通常比较困难。文献[7]在考虑最大海浪干扰下提出H∞控制来保证鲁棒稳定性，但是减摇性能比较保守。上述研究主要从升沉和纵摇运动的镇定问题来考虑，并没有考虑高速多体船减摇性能的优化[8-9]，而实际上减摇的目标是希望升沉和纵摇运动幅度尽可能地小，因此减摇控制尚需完善。

与H∞鲁棒控制不同，预测控制不仅考虑镇定控制，而且追求优化控制性能。预测控制根据被控对象的历史数据和模型信息来预测系统未来的输出，采用滚动优化方式获得未来输入，根据系统的输出实时校正预测模型来减少鲁棒控制的保守性，提高控制性能[10-12]。文献[13]建立了高速多体船的状态空间模型，采用预测控制与H∞鲁棒控制进行减摇性能对比，结果表明预测控制的减摇性能明显高于H∞鲁棒控制，其原因在于：1)预测控制可以直接处理升沉和纵摇强耦合的多变量模型，不需要文献[4]的复杂解耦矩阵设计；2)预测控制的滚动优化提高了减摇性能和鲁棒性，不需要文献[7]保守地假设海浪干扰的最大值。但是，预测控制采用序列二次规划(QP)在线求解控制量，计算量过大，严重影响了实际应用。因此，降低预测控制的计算量是必须解决的问题。显式预测控制采用离线设计和在线增益调度相结合，计算量较少，但是当离线区域划分过多时在线增益调度计算量也较大[14]。文献[15]提出连续解析预测控制，不需要在线调度参数，有效减少了预测控制的在线计算量，在高超声速X-33验证机的再入制导上得到验证，取得了良好的效果，但是解析预测控制律中并没有明确考虑模型不确性，以及风、浪、流等外部强干扰的影响，鲁棒性有待进一步提高。

本文针对高速多体船的升沉和纵摇运动耦合以及减摇性能优化问题，提出计算量少的解析预测控制。建立T型翼和压浪板作为减摇附体的高速多体船垂向控制模型，基于误差反馈校正的模型进行预测，采用数值积分方法获得解析连续预测控制律，提高减摇控制的实时性，给出闭环系统的一致有界理论分析。最后，给出解析预测控制方法与广义预测控制等其他方法的减摇性能仿真对比，通过实验验证了所提方法的有效性。

1 高速多体船的垂向运动模型

将T型翼和压浪板作为减摇附体，利用T型翼和压浪板翼面角度变化生成的恢复力和力矩来抑制减少升沉和纵摇变化幅度。建立高速多体船的运动坐标系如图1所示。以船舶的重心位置为坐标原点O，x轴正方向由船尾指向船艏；y轴垂直于船舶纵剖面且指向船舶左舷；z轴与水平面相垂直，背向地心。图1中w、φ分别为升沉位移和纵摇角。

假设多体船以稳定航向和定常航速在无限深的水域行驶，忽略风和流等干扰，高速多体船的垂向运动模型[12]为

(1)

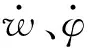
在模型(1)式中，纵摇和升沉运动存在加速度、速度、位移等变量强耦合，并且水动力学系数很难精确获得，存在较强不确定性，给多体船的减纵摇控制带来了困难。为便于控制器设计，将升沉和纵摇的耦合运动模型转化为

(2)

式中：

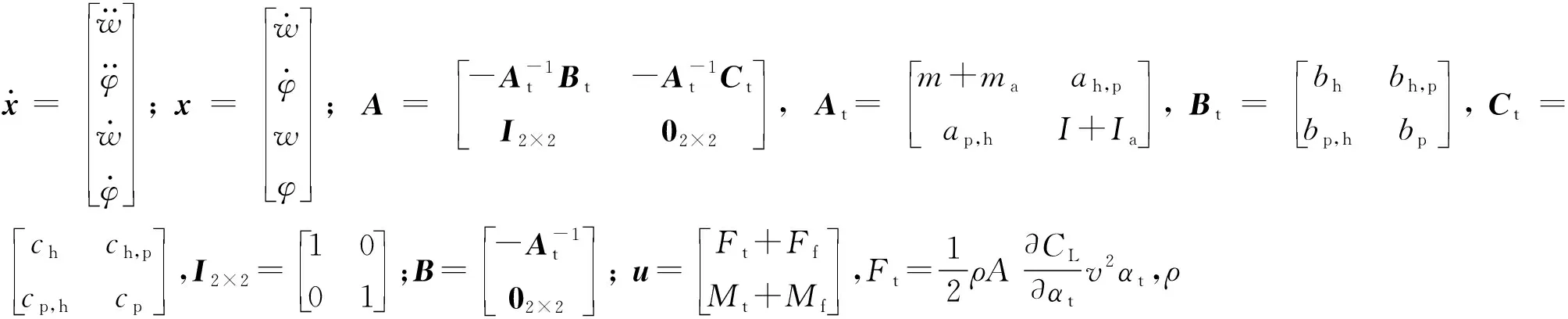
2 基于误差反馈校正的解析预测控制

2.1 传统的解析预测控制减摇

为优化高速多体船的减摇性能，提出连续解析预测控制减摇。定义减摇预测控制的连续优化目标函数为

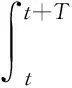
(3)

式中：t为当前时刻；T为控制时域，δc≤T<∞，δc为定义系统一致能控常数；Q、R分别为状态与控制的加权矩阵，Q≥0，R>0. 为了提高减摇控制的动态性，以及保证有限时域优化的稳定性，这里引入终端等式稳定约束，

x(t+T|t)=0，

(4)

式中：x(t+T|t)表示基于t时刻对t+T时刻的预测状态。则预测控制减摇转化为如下优化问题：

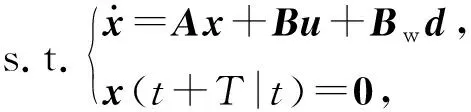
(5)

式中：u*(t)为最优控制输入。

文献[15]中提出了解析快速预测控制方法，采用1阶欧拉法近似描述预测模型，即

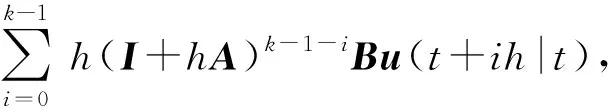
(6)

2.2 误差反馈校正的解析预测控制减摇

由于预测控制本身具有误差反馈校正功能，这里将实际x(t)与预测x(t|t-h)进行比较、得出预测误差，利用预测误差对名义模型的预测值进行反馈校正，使得连续解析预测控制具有一定的抗扰动和克服系统不确定性的能力。

定义t时刻的误差为

e(t)=x(t|t)-x(t|t-h)，

(7)

式中：x(t|t)=x(t)。则基于误差反馈校正的一步预测模型为

x(t+kh|t)=(I+hA)x(t+(k-1)h|t)+
Bu(t+(k-1)h|t)+ξe(t)，

(8)

式中：ξ为反馈校正系数。进一步迭代，得

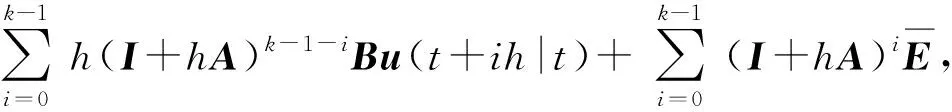
(9)

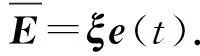
J≈h(0.5L(0)+L(1)+…+L(k)+
…+L(N-1)+0.5L(N))，

(10)

式中：L(k)=xT(t+kh|t)Qx(t+kh|t)+uT(t+kh|t)Ru(t+kh|t).令vT=[uT(t|t)，uT(t+h|t)，…，uT(t+(N-1)h|t)]，将目标函数写为如下紧凑形式：

(11)

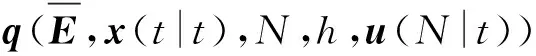
由(4)式、(9)式可得到终端等式约为

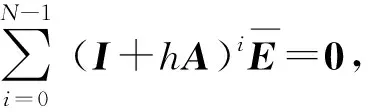
(12)

式中：M(N，h)为关于N、h的矩阵函数。

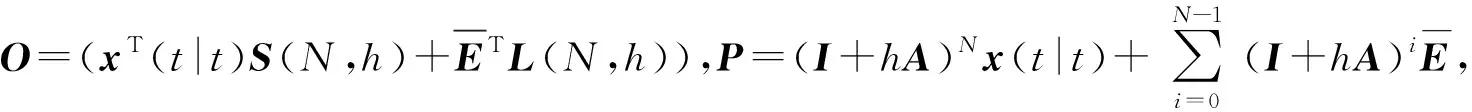
(13)

对v和λ求偏导，根据泛函最优的必要条件有(14)式[16]成立：

(14)

(14)式变换为如下形式：

(15)

若拉格朗日矩阵(15)式存在逆矩阵[17]

(16)

式中：E=H-1-H-1M(MTH-1M)-1MTH-1；F=H-1M(MTH-1M)-1;D=-(MTH-1M)-1。则可获得如下解析形式的最优控制序列：

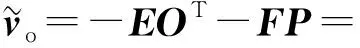
(17)

由于预测控制只选取当前的控制序列，控制输入为

(18)

式中：Km=[I2×2,02×2,…,02×2]。

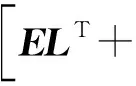
2.3 解析预测控制性能和稳定性分析

2.2节提出的解析预测控制与显式预测控制，以及文献[17]的离散预测控制相比较，具有如下特点：

1)多体船的整个航行包络空间较大，若采用显示预测控制，离线需要划分很多区域，进而导致在线增益调度花费很多时间。本文提出的解析预测控制律(17)式不需要在线调度参数，减少了区域搜索时间。

2)预测模型(8)式是连续的，时间步长h可以动态调整，具有自适应性，h越小预测模型越准确，控制性能越好。基于离散模型的解析预测控制结构是固定的[18]，不具有自适应性，没有考虑终端等式约束x(t+T|t)=0的情况，稳定性通过调节预测时域和控制时域得到保证。

为分析控制律(17)式作用下闭环系统的稳定性，本节分为两个步骤证明：

1)对于无干扰系统的有限时域最优控制可写为

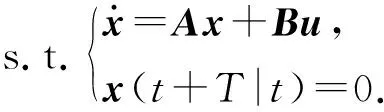
(19)

文献[19]给出了对于任意控制时域T的稳定控制律，即

(20)

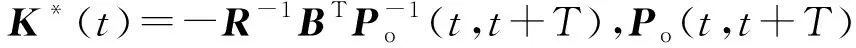
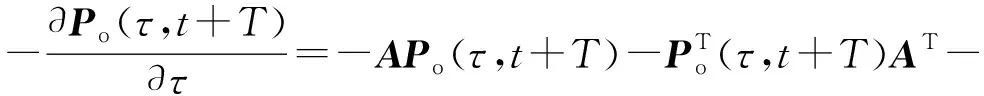
(21)

Po(t+T,t+T)=0.

(22)

采用控制律(20)式系统是一致渐近稳定的，并且存在Lyapunov函数：

V=xTFo(t)x，

(23)

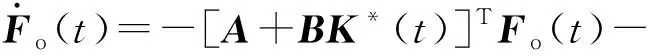
(24)

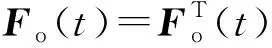
2)在最优控制(20)式下的渐近稳定基础上，分析控制律(17)式作用下的闭环系统稳定性为

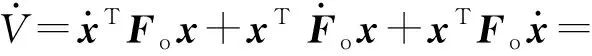
(25)

由(17)式可知

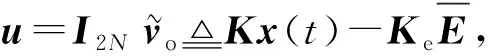
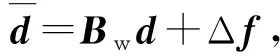
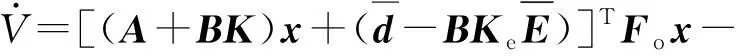
(26)

对于(26)式中的第1项，文献[15]给出证明：

u(t)-u*(t)=[K-K*]x(t)=
hΩ(t；N,h)x(t)，

(27)

式中：

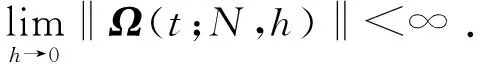
(28)

由(26)式可知，对于任意的正定QF>I4×4，总能找到h=T/N，使得

xT{[K-K*(t)]TBTFo+
FoB[K-K*(t)]+I4×4-QF}x=
xT{h[ΩT(t；N,h)BTFo+FoBΩ(t；N,h)]+
I4×4-QF}xT<0.

(29)

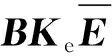
(30)

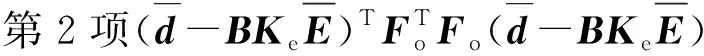
3 仿真分析

3.1 海浪干扰仿真

高速多体船在4级海浪中以40 kn的航速行驶，遭遇频率取3.25 rad/s，遭遇角为180°迎浪航行，有义波高为2 m.海浪干扰选用国际拖曳水池会议(ITTC)单参数谱作为海浪仿真谱函数[20-21]，即

(31)

式中：ω为海浪主导频率；hw为海浪有义波高；g为重力加速度。高速多体船主要包括双体船和三体船两类，仿真中以三体船为例进行研究。三体船在航行时，对水线下部分进行切片计算可以得到船舶受到的海浪干扰力和力矩。求解三体船在不同频率点下的海浪干扰力和干扰力矩分别为

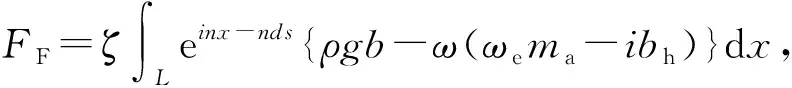
(32)

式中：ζ为海浪波高；L为船体长度；n为波数；d为船舶吃水；s为复变量；b为船宽；U为船速；ωe为海浪的遭遇频率。由(32)式可得到多体船受到升沉力和纵摇力矩谱HF(ωe,β)和|HM(ωe,β)|。令ΦF(ωe,β)为干扰力功率谱，ΦM(ωe,β)为干扰力矩功率谱，Φζ(ωe,β)为遭遇海浪功率谱。根据

ΦF(ωe,β)=|HF(ωe,β)|2Φζ(ωe,β)，
ΦM(ωe,β)=|HM(ωe,β)|2Φζ(ωe,β).

(33)

对(33)式进行逆傅里叶变换，采用数据拟合和叠加的方法，得到随机海浪作用于三体船的干扰力和干扰力矩，分别如图2、图3所示。

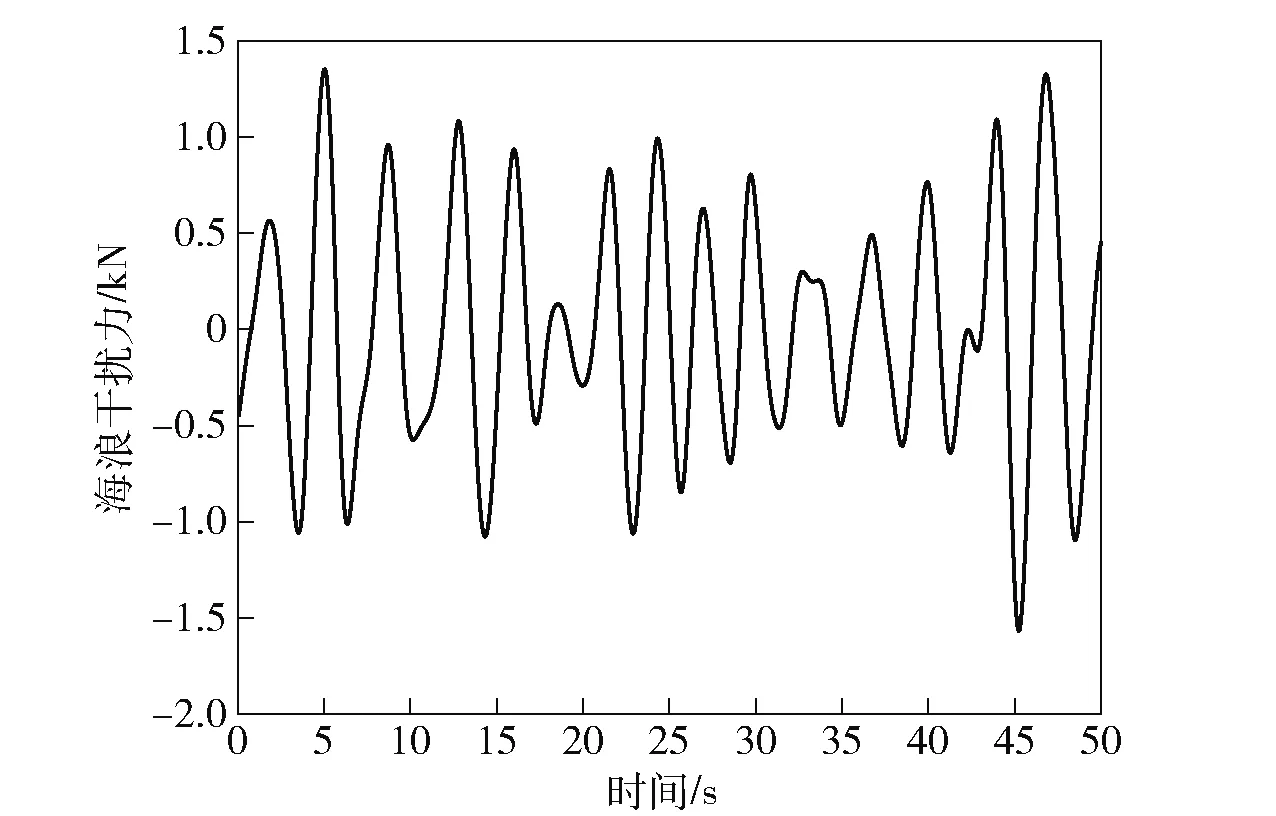
图2 海浪干扰力Fig.2 Wave disturbance force

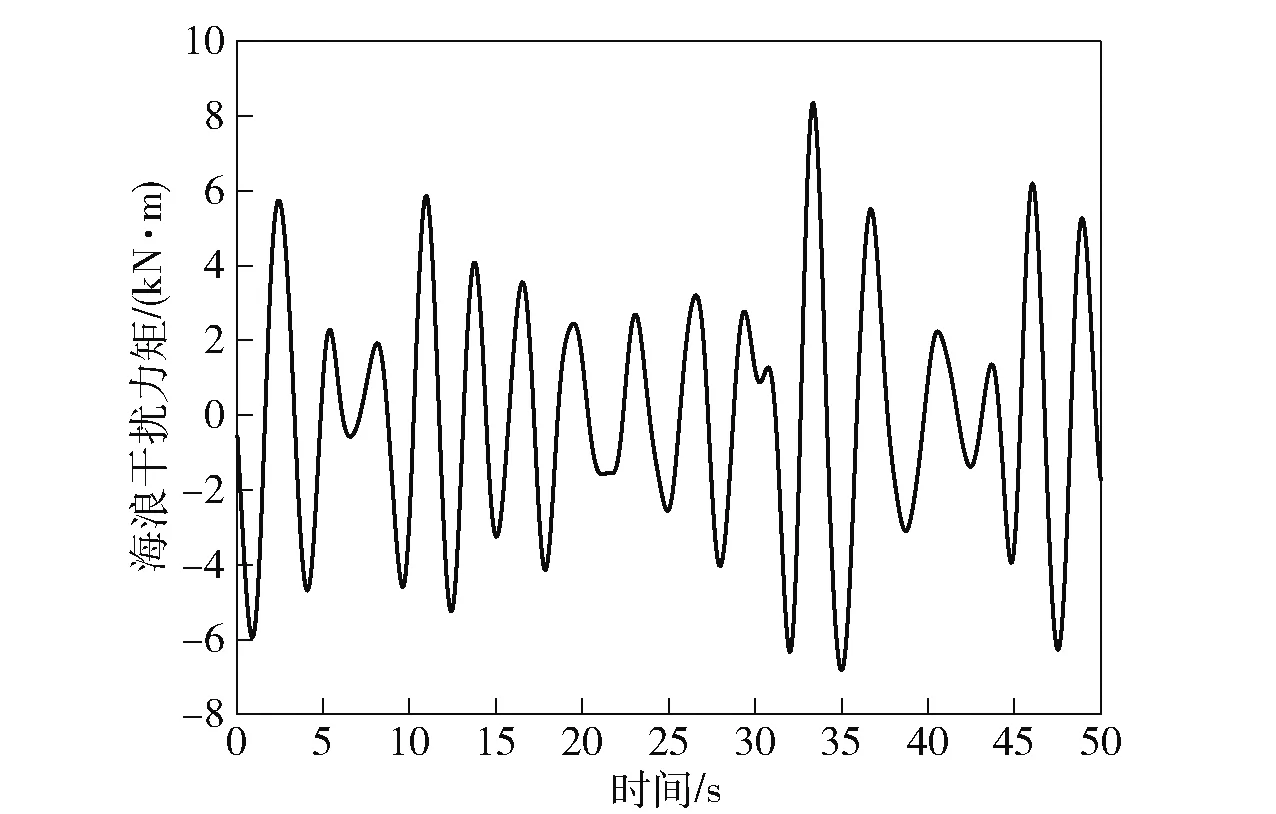
图3 海浪干扰力矩Fig.3 Wave disturbance moment

3.2 解析预测控制性能仿真

考虑多体船航速影响，依据切片理论对多体船运动参数求解，可以得到某三体船在某特定频率下的一组三体船参数如下：A=

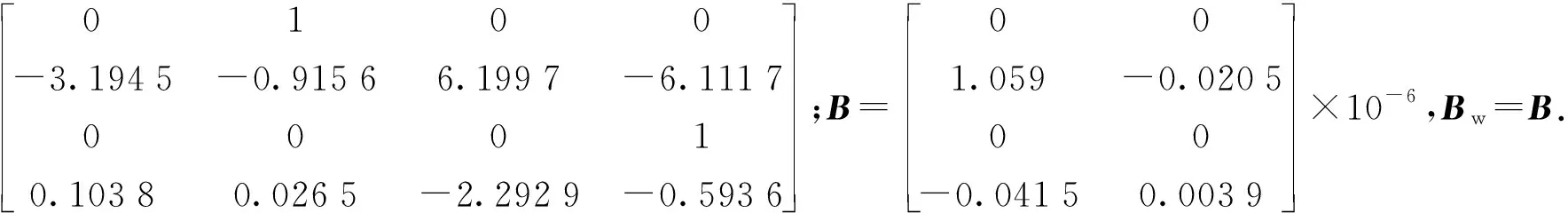
本文所提解析预测控制律结构与预测步数N有关。预测步数越多，控制性能越好，但是控制器结构复杂，实际中一般选为3或者4，这里N取4.当N固定时，时间步长h的选取将直接决定预测模型的精确性，影响控制效果。当时间步长h分别为0.4 s、0.5 s和0.6 s时仿真结果如图4和图5所示。从图4和图5中可以看出，时间步长h越小，升沉和纵摇减摇性能越好，其原因是h越小、预测模型越准确，控制量变大。实际中T型翼和压浪板的输入攻角有严格幅值约束，容易出现饱和现象，因此步长h需要折中选择，这里h=0.5 s.

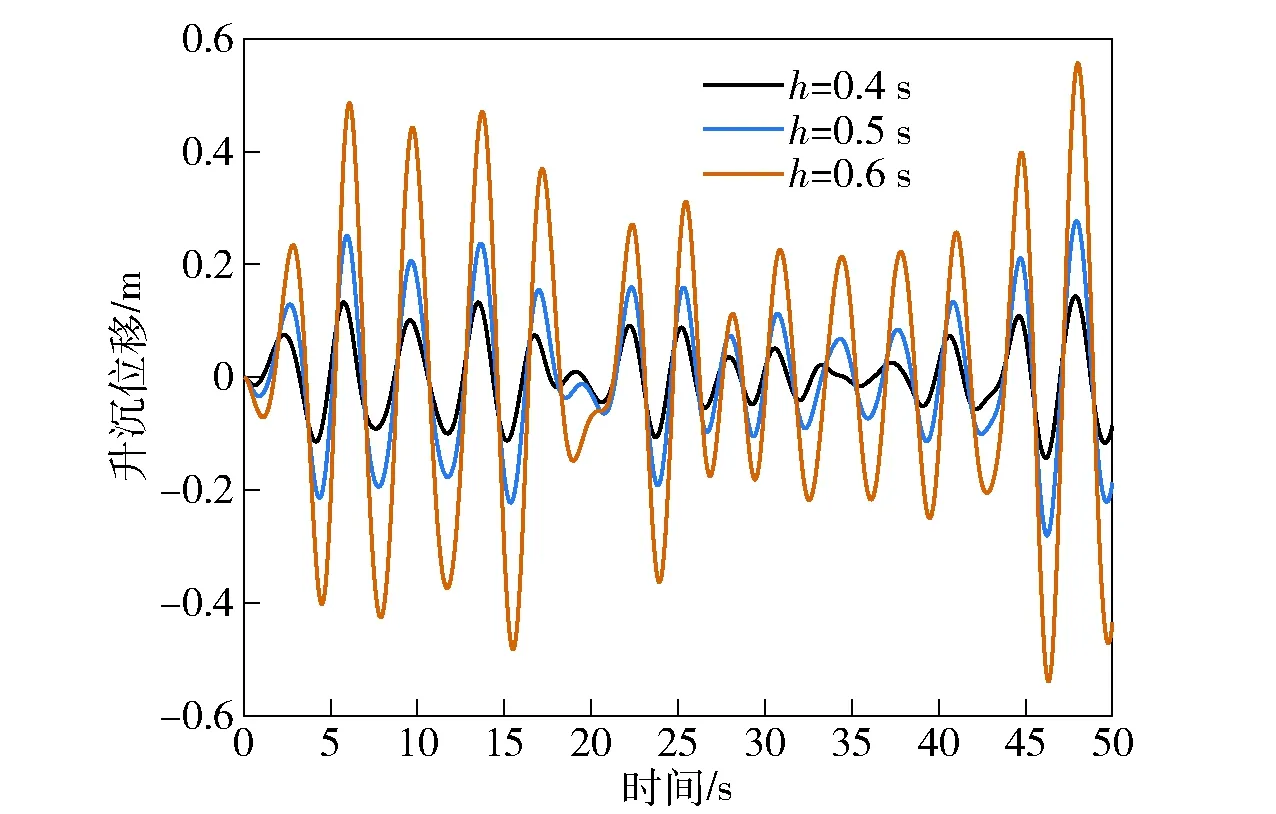
图4 不同时间步长的三体船升沉运动Fig.4 Heaving motion of triple-hulled vessel at different time steps

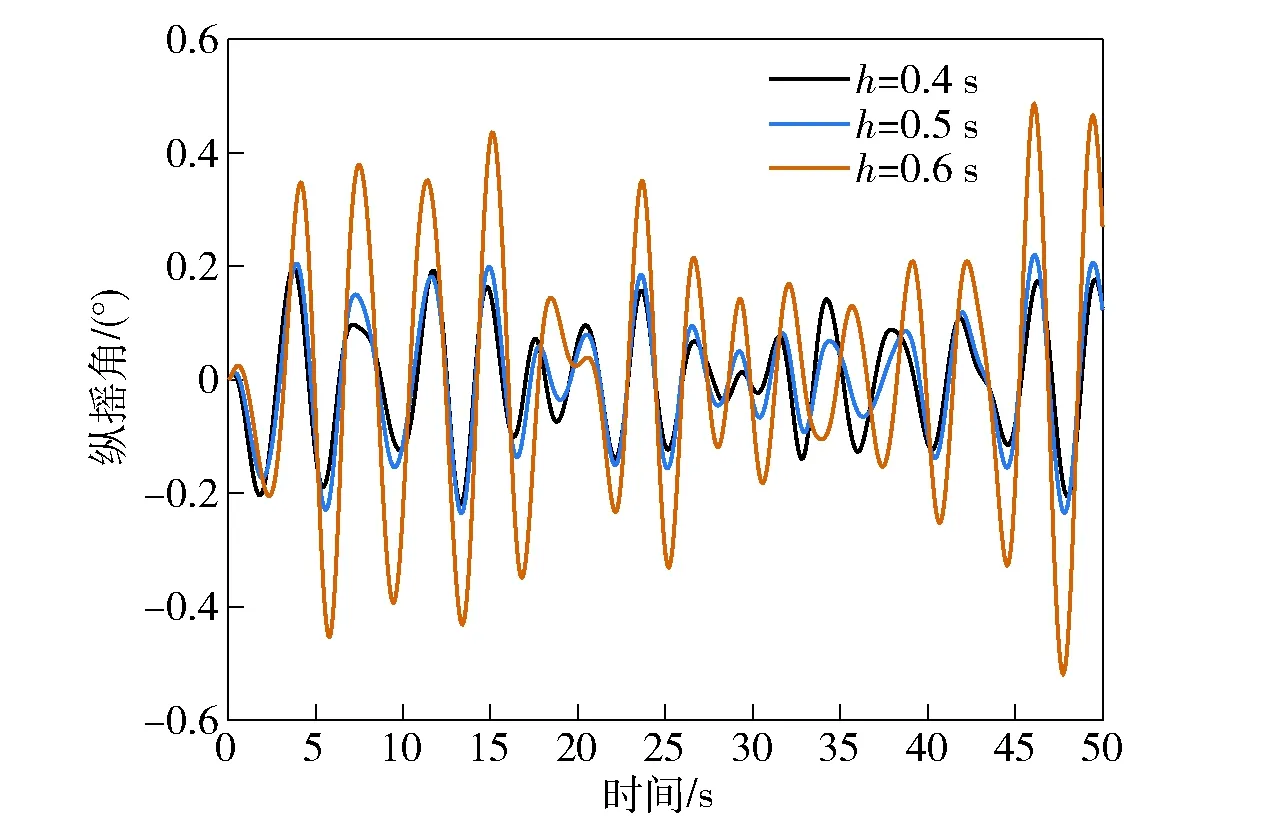
图5 不同时间步长的三体船纵摇运动Fig.5 Pitching motion of triple-hulled vessel at different time steps

3.3 减摇控制性能对比

分别进行没有控制、文献[9]的广义预测控制、文献[12]的解析预测控制、基于误差反馈校正的解析预测控制4种情况下的多体船垂向运动对比(见图6～图9)，减摇数据如表1所示，其中3种预测控制律的加权矩阵都选为Q=diag(1,1,1,1)，R=diag(1,1)，预测步数皆取为4.

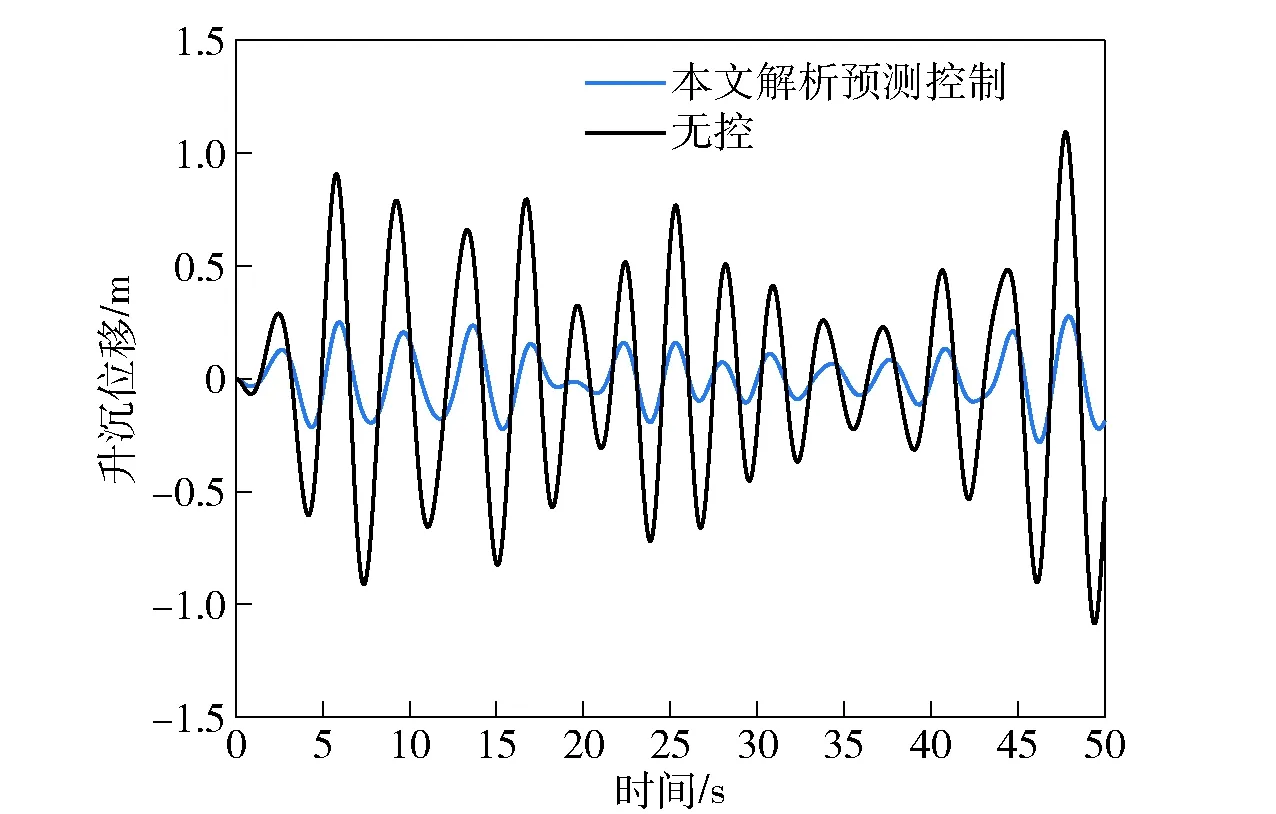
图6 三体船的升沉运动Fig.6 Heaving motion of triple-hulled vessel

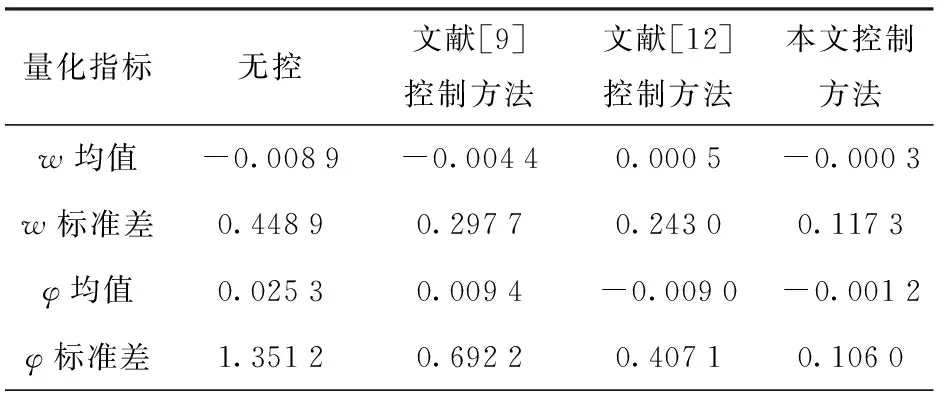
表1 三体船升沉和纵摇运动的减摇仿真

图6和图7所示为无控和考虑误差反馈校正的解析预测控制减摇控制对比，从中可以看出升沉和纵摇运动幅度明显减少，升沉运动量减少60%左右，纵摇运动量减少80%左右，表明解析连续预测控制是有效的，不需要传统预测控制的在线优化。

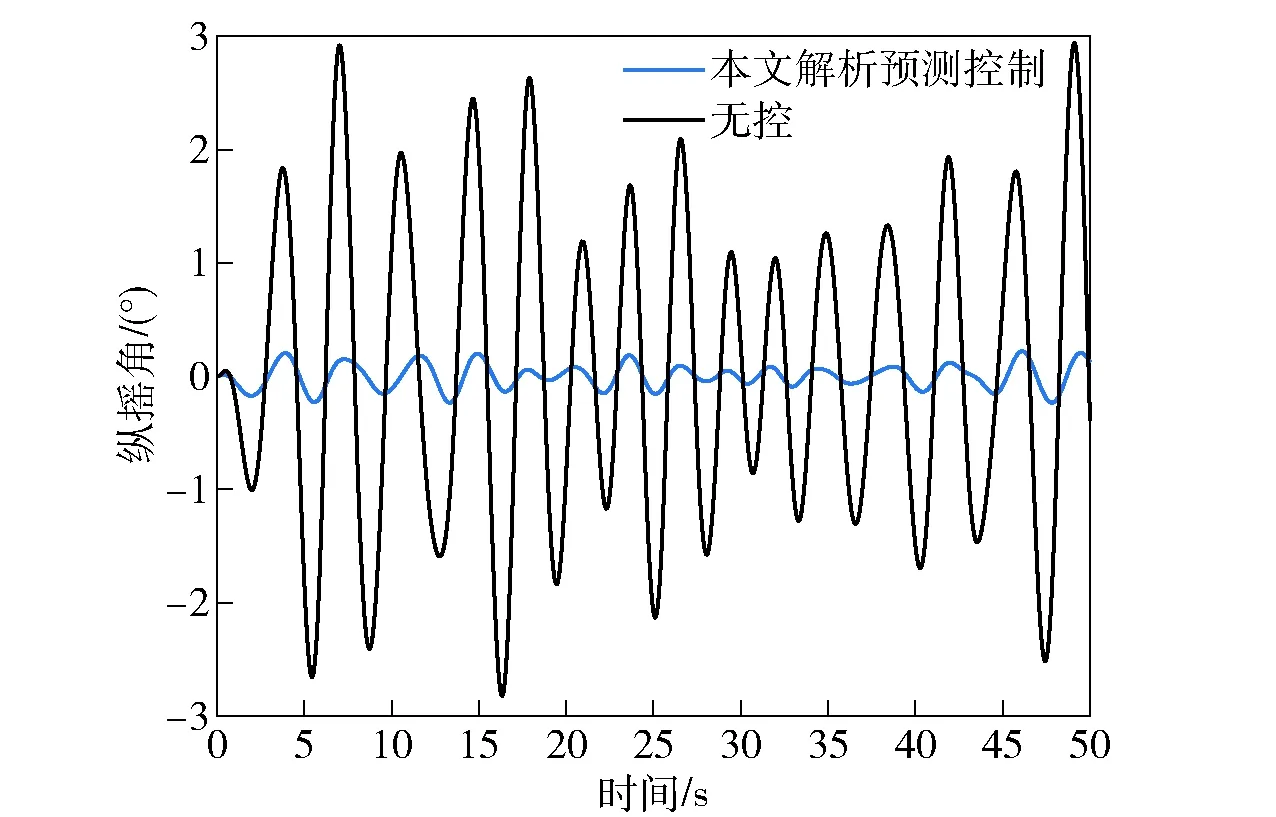
图7 三体船的纵摇运动Fig.7 Pitching motion of triple-hulled vessel

将文献[9]的广义预测控制与文献[12]的解析预测控制进行对比，如图8和图9所示。从图8和图9中可以看出，文献[12]的解析预测控制减摇效果更好，这是因为相对于文献[9]，该方法明确考虑了终端等式约束，提高了控制性能。但是，由于其预测模型没有考虑随机干扰和参数不确性，减摇性能还没有达到理想效果。图10和图11所示为文献[12]和本文所提基于误差反馈校正解析预测控制减摇控制的对比，从中可以看出基于反馈校正的解析预测控制进一步减少升沉和纵摇运动幅度，对海浪干扰具有更强的抑制能力，其原因是误差反馈校正提高预测模型的精度，减摇性能变好。

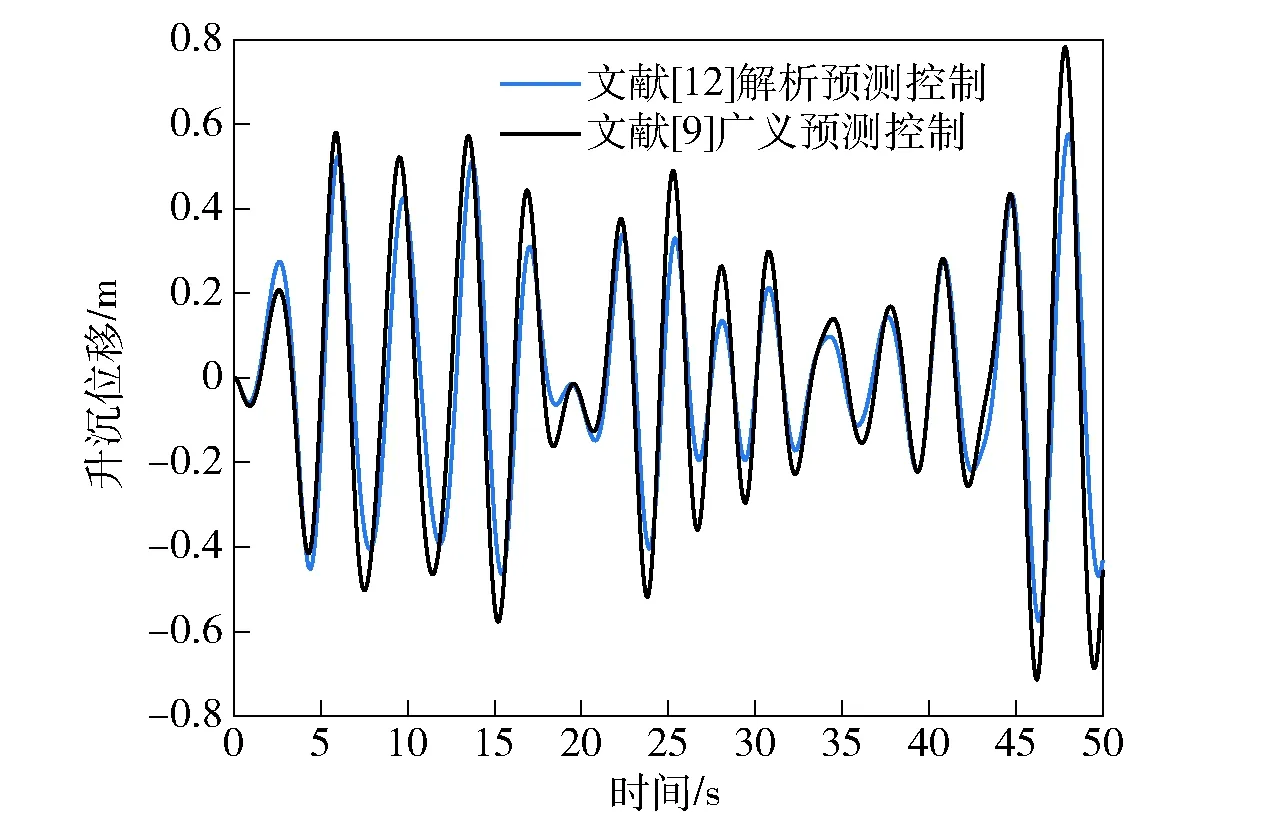
图8 不同控制律的三体船升沉运动Fig.8 Heaving motions of triple-hulled vessel with different control methods

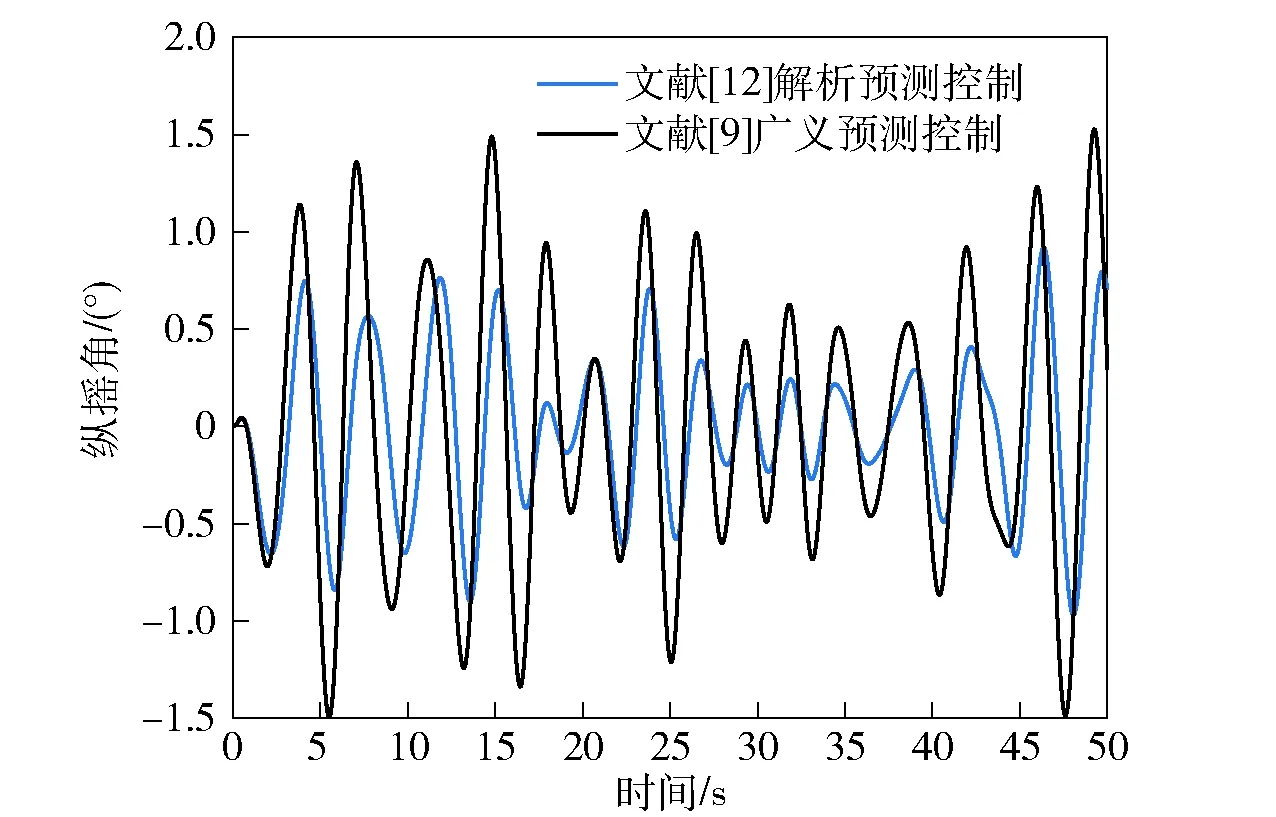
图9 不同控制律的三体船纵摇运动Fig.9 Pitching motions of triple-hulled vessel with different control methods

4 实验验证

设计一艘小型的实验三体船，如图12所示。三体船船体材料选为玻璃钢，因为玻璃钢具有耐腐蚀、质量小、机械强度高等优良特性。甲板部分材料选为铝板，主要避免焊接时的变形。工控机和嵌入式底层控制板放在三体船舰岛舱室，三体船内部为相关传感器、电源以及相关线路，三体船外形尺寸参数如表2所示。三体船的减摇附件选型为T型翼和压浪板，在船艏底部安装T型翼，用来降低多体船的垂向运动幅度，在船尾安装压浪板，用来减少航行阻力。T型翼和压浪板为液压驱动(见图12)，优化后的附体参数见文献[9]。

图12 装有T型翼和压浪板的三体船Fig.12 Triple-hulled vessel with T-foil and flap

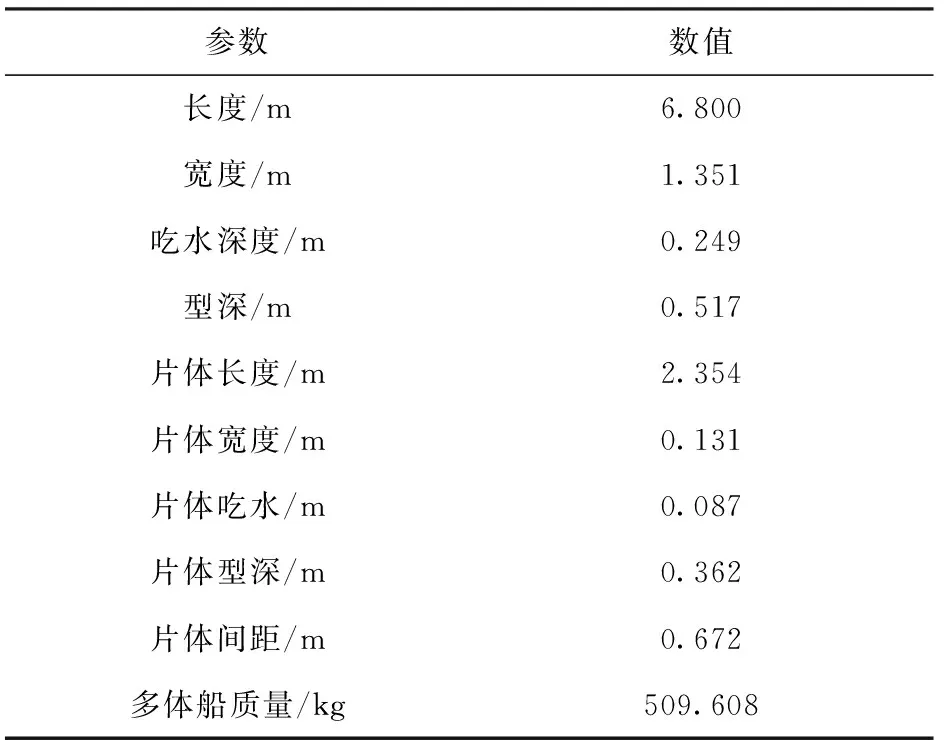
表2 三体船参数

实验三体船的控制系统上位机选用工控机，工作平台采用Windows XP系统和VC++6.0，实现三体船运动轨迹显示和设置工作参数，主要包括人工操作界面、串口通讯模块、各传感器检测参数、升沉和纵摇显示界面。实验三体船的底层减摇稳定控制系统选用 ARM7 架构的 LPC2294 芯片作为主控芯片，内嵌 UC/OS-II 操作系统，微处理器接收升沉传感器和纵摇传感器量测的多体船运动信息，采用本文提出的解析预测控制算法实时解算T型翼和压浪板的控制量，驱动液压缸执行机构，构成闭环减摇控制系统。三体船升沉位移和纵摇角传感器的数据采用串行通信方式与工控机通讯，工控机对传送来的数据进行存储和显示，便于实时监测和控制。

根据Froude缩放定律，实验中采用10∶1的船舶模型，4级海况下波高为0.2 m，周期为2.06 s. 图13所示为多体船实验场景，船模航行速度为6.507 3 m/s. 实验结果如图14和图15所示，从中可见在本文所提预测控制下升沉和纵摇运动幅度明显下降，其中升沉运动幅度下降了40%左右，纵摇运动幅度下降了70%左右(0～70 s)，减摇效果与仿真数据相比有一定差距。这是因为实验三体船的水动力学参数与仿真模型数据有一定差距，并且升沉/纵摇传感信号有较大的量测噪声影响减摇效果，后续将对信号滤波和减摇的鲁棒性进一步研究。

图13 实验验证Fig.13 Experimental verification

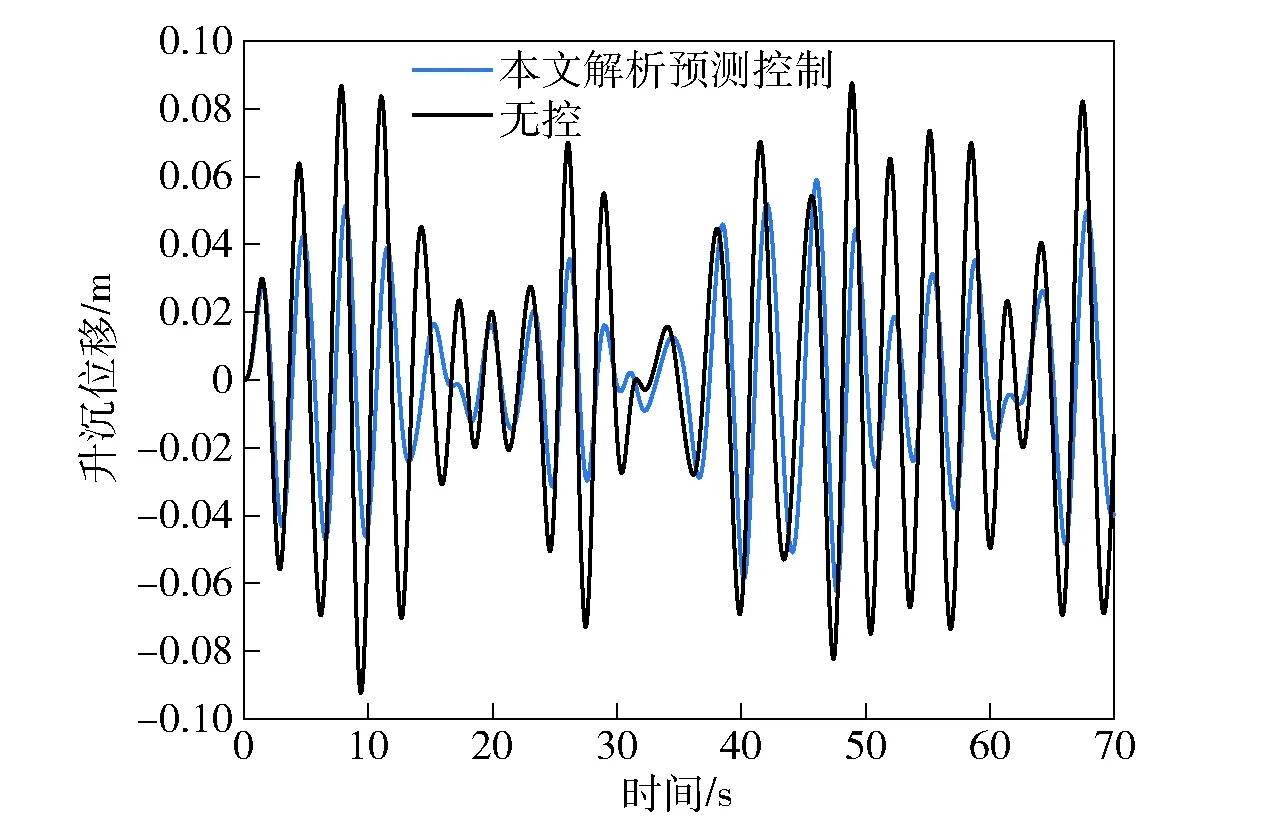
图14 实验三体船的升沉运动Fig.14 Heaving motion of triple-hulled vessel

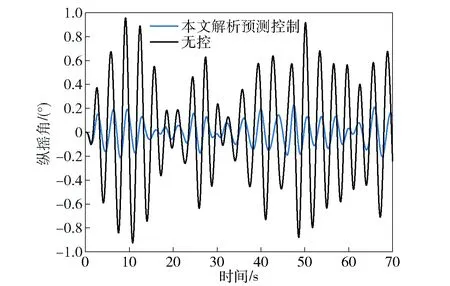
图15 实验三体船的纵摇运动Fig.15 Pitching motion of triple-hulled vessel

5 结论

本文针对高速多体船在恶劣海况下纵摇和升沉运动幅度过大的特点，提出了计算量少的的解析预测控制减摇方法。得出主要结论如下：

1)基于误差反馈校正和1阶欧拉模型预测升沉和纵摇运动状态，提高预测模型精度；采用数值积分和最优二次序列规划理论获得多体船减摇的解析预测控制律，减少预测控制在线优化的复杂性。

2)基于Lyapunov稳定性理论分析闭环系统的一致有界性，并与广义预测控制等其他方法进行了性能对比，通过仿真和实验验证了所提方法的有效性。