直喷发动机燃油喷雾特性经验公式定量研究

王森，顾鹏,2，袁志远，徐宏昌

(1.上海交通大学机械与动力工程学院，上海 200240；2.上汽通用汽车有限公司，上海 201206)

燃油喷雾特性对内燃机燃油经济性与尾气排放具有重要影响，因此，发展燃油喷雾模型是内燃机设计的关键环节。许多前期研究对燃油喷雾特性进行了全方位研究，并总结了大量经验公式，用以刻画诸如喷雾贯穿距、喷雾锥角等特性。部分经验公式，如1960年以来Wakuri等[1]、Naber等[2]基于动量理论与大量试验数据得出的柴油喷雾经验公式，由于其使用的广泛性与预测的精确性，已被应用于喷雾建模的过程中。近年来，Payri[3]、曾伟等[4]基于无量纲分析提出了汽油喷雾特性经验公式，同样具有较好的预测效果。

但需要指出和注意的是，多数面向燃油喷雾的经验公式受限于自身的假设前提，应用范围较窄。例如，Sazhin等[5]在获取喷雾贯穿距经验公式时假设：虽然空穴现象的产生对于燃油速度与流量影响均较为显著，但对于动量流量的影响可以忽略不计。与之类似，Siebers等[2]在推导喷雾锥角经验公式时也使用了理想质量、动量流模型[6]。因此，对于现有模型进行比较分析，明确其局限性、验证其适用性具有重要意义。

此外，不同经验公式适用工况存在较为明显的差异。例如，Hiroyasu等[7]提出的喷雾贯穿距经验公式是基于低喷射压力、低背压试验数据得出，但许多其他研究工作是在柴油机实际工况下进行的。因此，明确经验公式的适用范围、油品特性以确保其适用性是极为重要的。

最后还需要指出，不同分析方法得到的经验公式结果通常难以直接进行比较，例如部分经验公式以实际参数为基准[2，5]，而部分经验公式则是基于无量纲准则数进行分析[3-4]，如何构建统一标准来衡量上述经验公式的适用性是急需解决的问题。不同类型内燃机的喷油器由于使用工况、燃油种类、喷嘴结构等不同，所以不同研究得出的经验公式都有自己的局限性。本研究希望从这些局限性中，找到它们的共通性，起到尽可能简化经验公式的效果，为工程应用和喷雾设计提供参考。

针对上述问题，本研究主要从试验数据出发，比较并分析不同经验公式的适用范围与准确程度。通过对不同结果与机理的阐述，建立经验公式选取标准，以期对汽油或柴油机喷雾全过程特性进行全面描述与指导。

1 现有主流研究结果总结

表1列举了应用较广的喷雾贯穿距、喷雾角经验公式，以下分别对贯穿距、喷雾锥角经典经验公式进行总结分析。

表1 喷雾贯穿距、喷雾锥角经验公式总结

1.1 喷雾贯穿距经验公式

Payri等[3]通过试验数据得出如下经验公式：

(1)

式中：S为贯穿距；Deq为等效直径；CV为节流孔出口处的速度系数；Ca为节流孔出口处的收缩系数；Uth为理论速度；t为时间；θ为喷雾锥角。式(1)基于如下假设：动量流动不受空穴生成的影响。式(1)的局限性在于对于经验参数cte的推导没有严格的数学证明，且这一参数的物理意义不够明晰，需要根据试验情况进行调整。

Sazhin等[5]总结以下经验公式用以描述喷雾贯穿距发展：

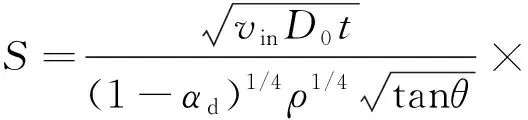
(2)

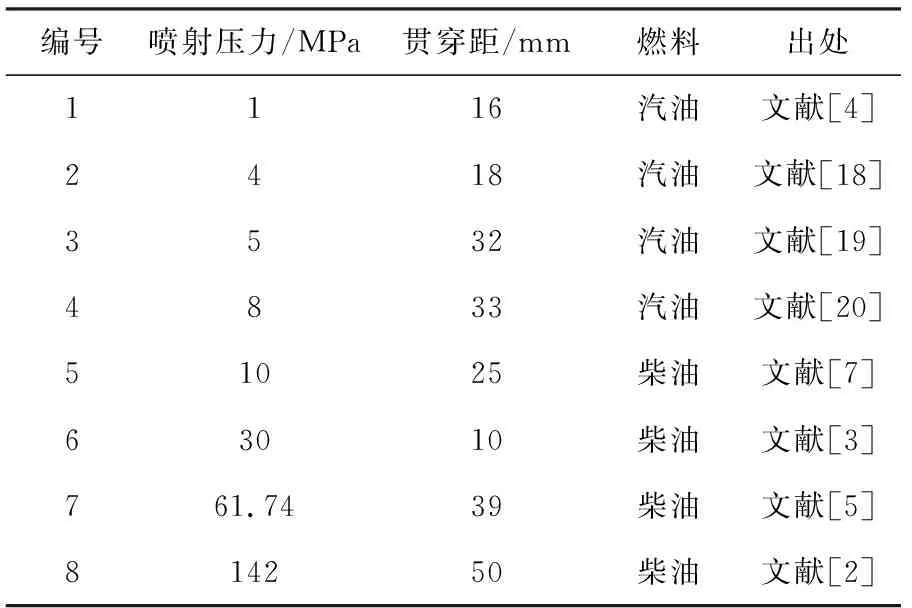
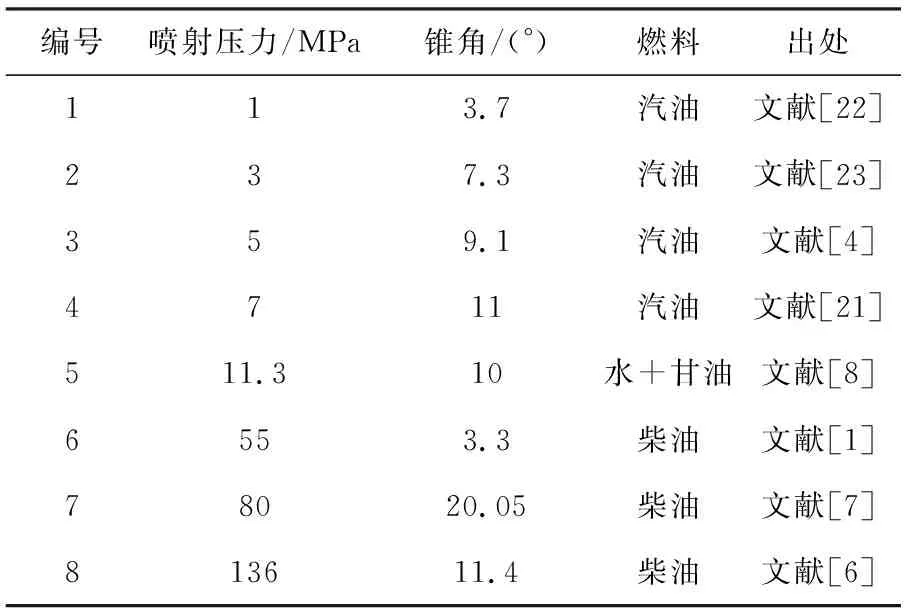
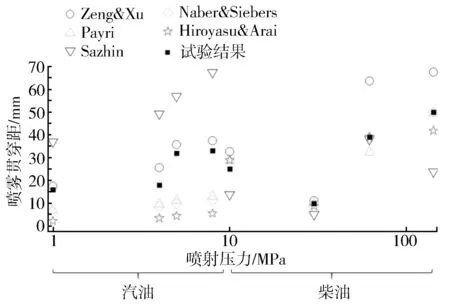
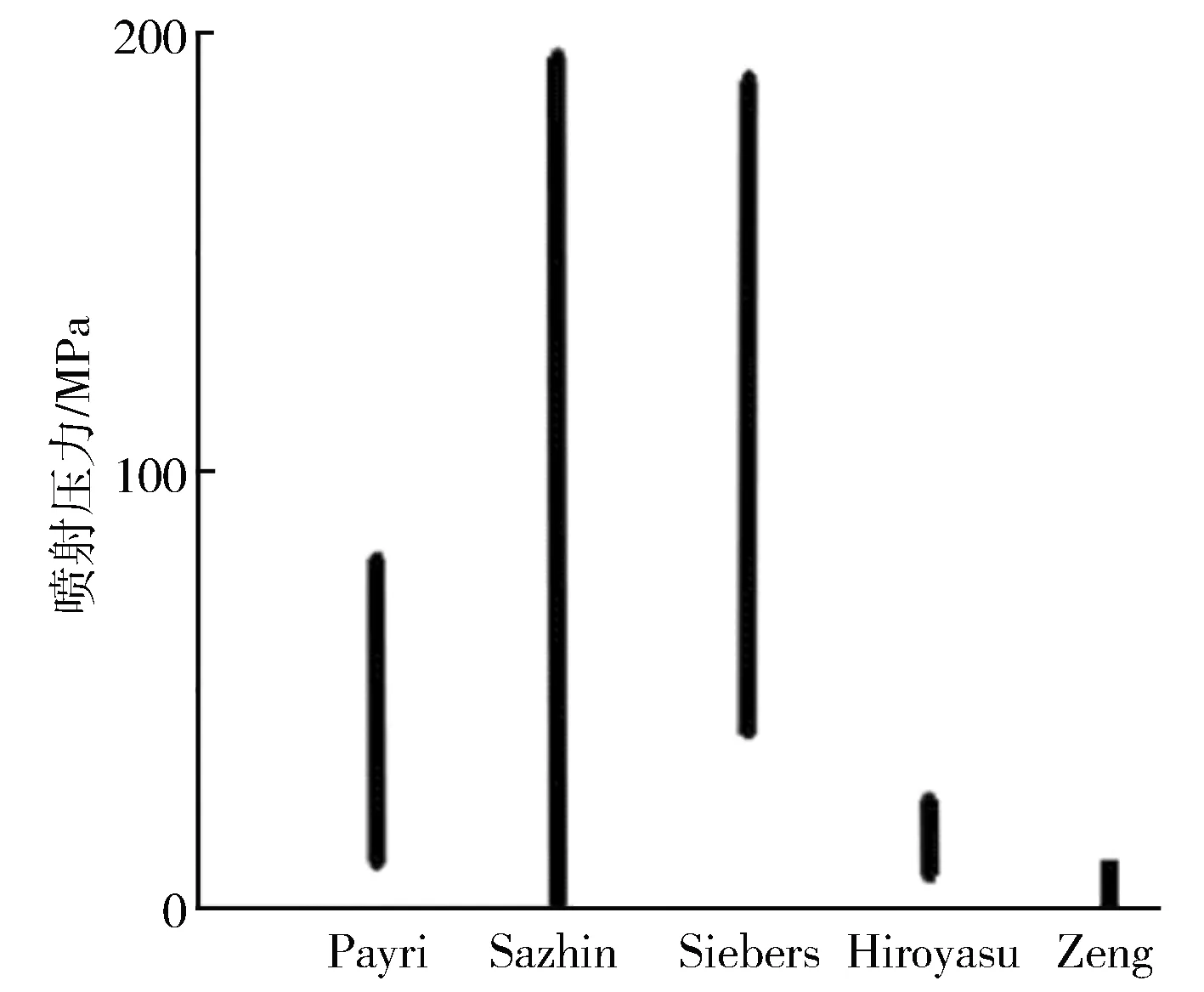
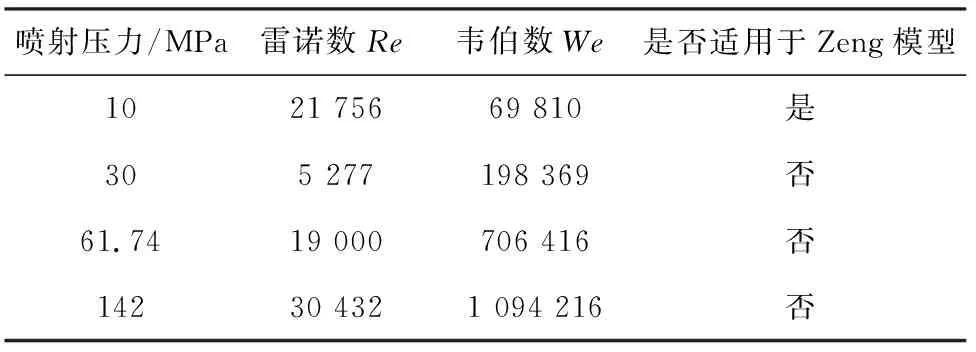
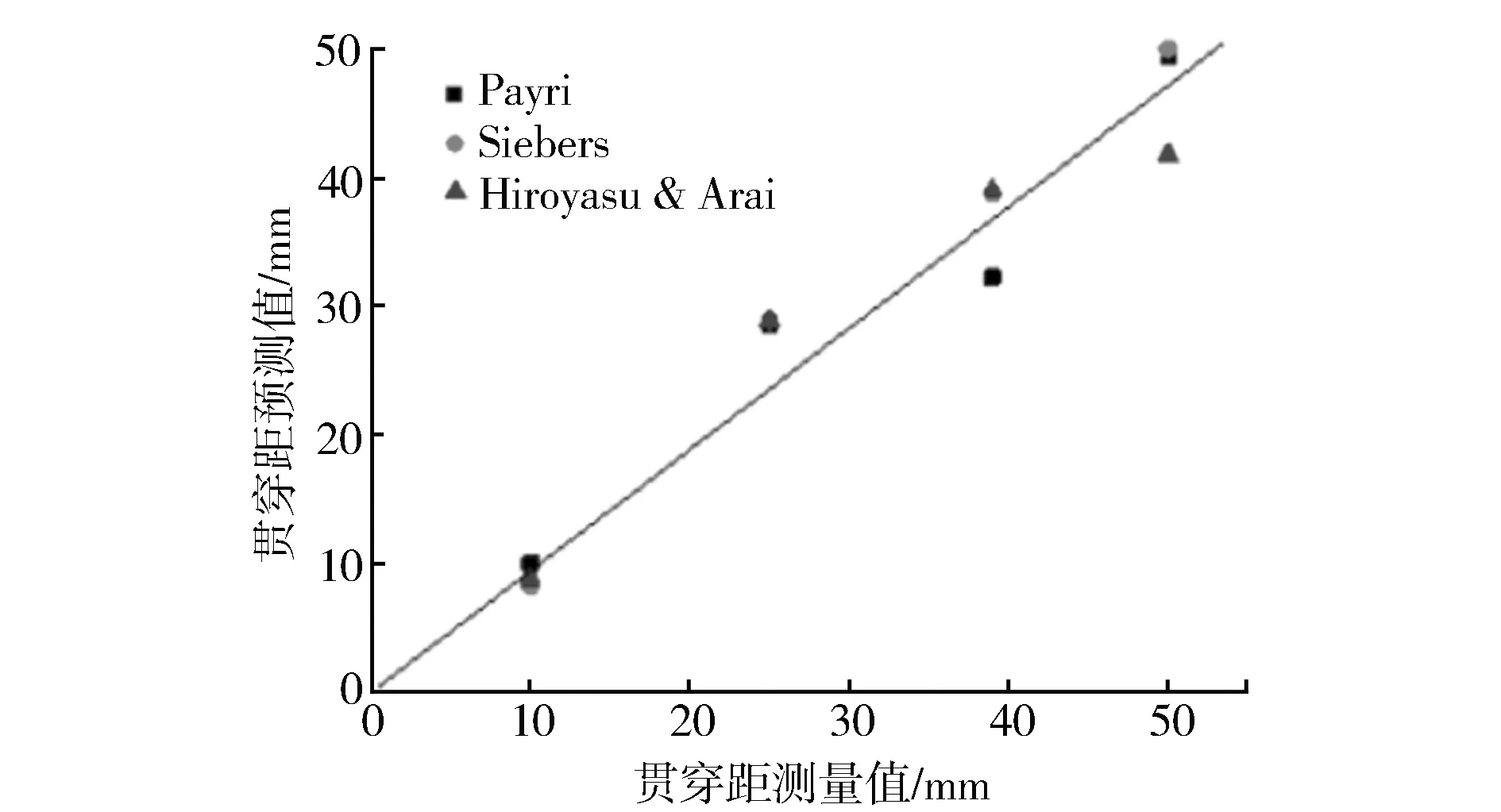
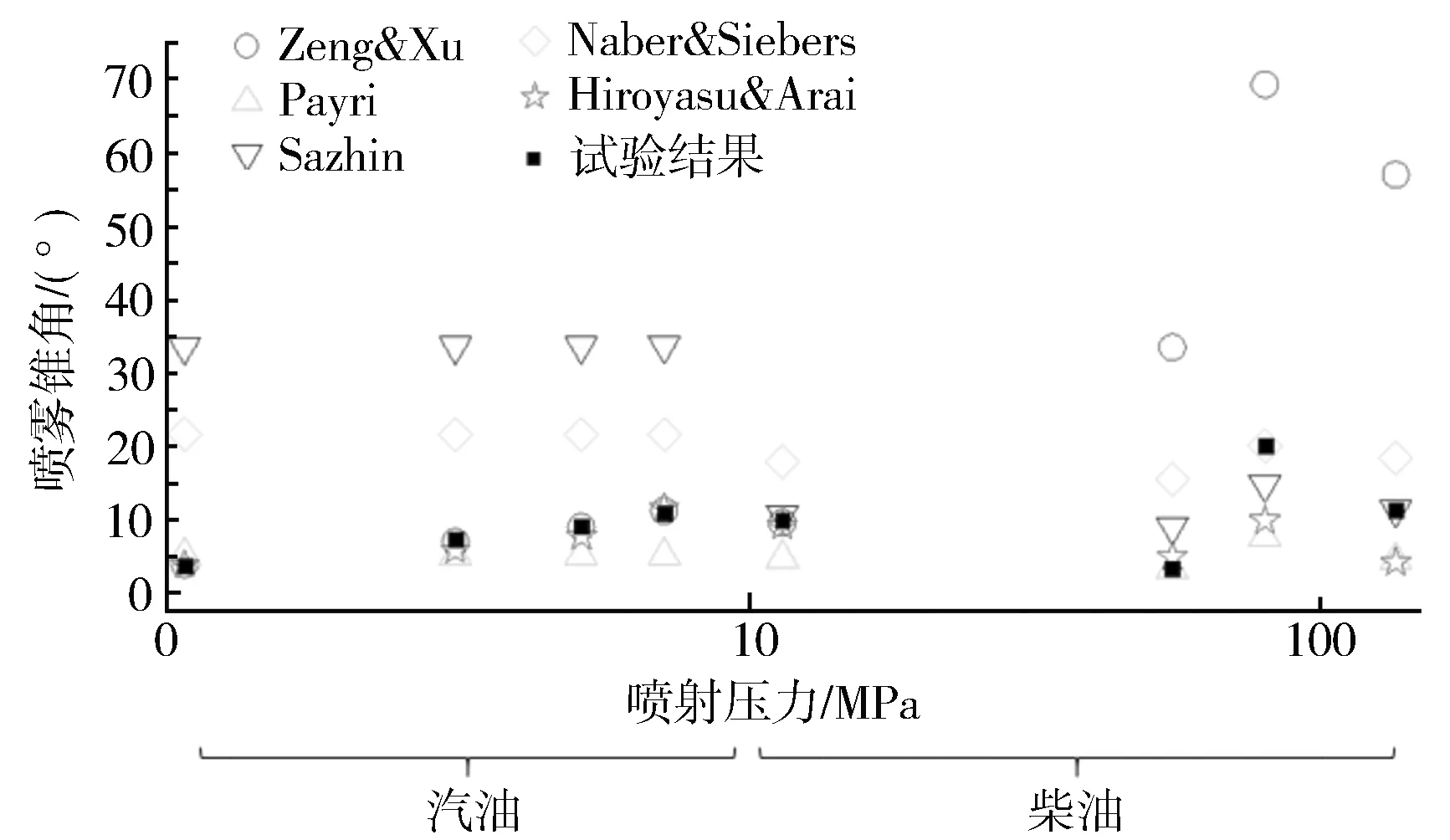
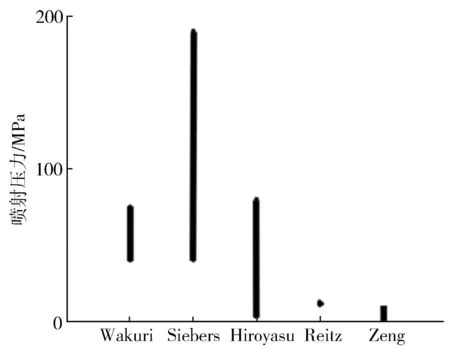
式中：vin为喷孔入口的喷雾速度；αd为液滴在喷雾中占据的体积分数。式(2)适用于以下三种场景：流体为斯托克斯流(Re<0.2)；流体为艾伦流(0.2

式(3)由Naber和Siebers[2]提出，用以描述喷雾贯穿距。式(3)同样具有局限性，特别是在将式(3)与Hiroyasu和Arai等[7]提出的经验公式进行对比时，其涉及到的喷嘴相关尺寸参数与喷雾锥角参数均需要进一步完善。

(3)

式中：Pf为燃油压力；Pa为环境压力；ρa为环境气体密度。

Hiroyasu和Arai[7]等基于柴油喷雾推导出了下列经验公式：

(4)

式(4)假定喷雾贯穿距可以根据破碎时间划分为两个区域， 公式中的部分参数与喷嘴设计直接相关，因此Naber和Siebers等[2]在式(4)基础上进行了改进，使之更具有普适性。

曾伟和许敏等[4]提出使用无量纲准则数对喷雾贯穿距进行预测，相应经验公式如式(5)所示。

S=0.076(ρa/ρl)-0.268We0.318Re0.152(Re<12 500)

(5)

这一经验公式基于喷射时刻后1.0 ms的贯穿距数据，因此这一公式无法对喷雾时序变化进行预测，同时，这一结果只考虑了冷态喷雾，对于喷雾微观结果或闪急沸腾气泡等相变因素的影响缺乏考虑。

1.2 喷雾锥角经验公式

Wakuri等[1]总结得出如下经验公式以描述喷雾锥角变化规律。

(6)

式(6)建立在两个重要假设基础之上。其一，当控制体内氛围气体密度较高时，液滴粒径，液滴与液滴、气相与液相混合的速度均可以忽略不计；其二，喷射燃油的质量流量可以等价转换为气液相混合的质量。上述两点假设不符合多数工况条件，会导致这一公式的结果存在较大误差。同时，喷射速度、喷孔直径等参数也会对结果造成影响，但研究中并未选取足够多的工况点进行拟合。

Siebers等[6]提供了两条描述喷雾锥角的经验公式，如式(7)、式(8)所示。

tan(α/2)=atan(θ/2)

(7)

(8)

该研究假定实际质量流量与动量均与理论值近似。但这一情况存在较为明显的缺陷。例如，常数a经由经验拟合获得。根据文献，常数a可以通过计算三种液相模型获取，但计算的过程却没有详细阐述。在分析式(8)时，试验使用了246 μm直径喷嘴，公式对于其他喷嘴是否具有普适性需要进行进一步验证。

Hiroyasu和Arai等[7]通过试验数据推导得到了式(9)，式(9)假定喷雾锥角会随着喷射压力提高而增大，但当喷射压力超出一定阈值时，喷雾锥角趋于稳定。式(9)具有局限性，主要是由于其只适用于高喷射压力下的稳定喷雾，而不能用于动态分析。其推导过程中存在的另一个问题如下：假设存在三条曲线分别表示三种不同黏度的燃料， 三者的稳定数值相近，但公式中只给出了三个关键参数，这导致了未知数数量等于方程数量，因此需要有额外的曲线进行验证，以得到更令人信服的结果。

(9)

式中：ρl为燃油液体密度。Reitz和Bracco[8]所给出的喷雾锥角预测模型如式(10)所示，这一模型只给出了曲线的大致形状，其权重与具体表达形式并未给出。与之相比，其他课题组研究所得出的曲线[9]在形状上具有较为明显的差异。

(10)

基于对现有的认同度较高的喷雾贯穿距、喷雾锥角经验公式的归纳与分析，以下进一步通过试验对比分析上述经验公式的适用性与局限性，从机理模型的角度出发，更全面地对上述经验公式进行分析。

2 经验公式定量分析

2.1 试验数据集整理

用于比较各经验公式结果的试验数据来自于诸多文献，工况点的选取主要遵从以下两个原则：

1) 所选择的工况点应尽可能位于多数经验公式的适用范围，以确保各经验公式的对比具有意义；

2) 所选择的工况点数量尽可能多，以确保评价可信度，同时将试验结果与预测值之间的差异最小化。

表2与表3分别列出了用于验证喷雾贯穿距与喷雾锥角经验公式的试验数据结果。其中表2所选择数据的时刻为喷射开始后1 ms，为便于直接比较，所选择的喷射具有相同的输入参数。需要说明的是，本研究对部分试验数据的参数进行了变换，以得到具有可比性的拟合曲线。

表2 喷雾贯穿距试验数据集

表3 喷雾锥角试验数据集

2.2 不同数据集结果对比

2.2.1 喷雾贯穿距结果对比

图1示出了全部工况下试验结果与经验公式解析解的对比结果。图中结果直接反映了各个经验公式对于喷雾贯穿距在不同工况下预测效果的准确性，可见经验公式的选取对于预测起到重要影响。

图1 喷雾贯穿距试验数据与经验公式预测结果对比

图2示出了各个经验公式的适用范围。 由图可知，Sazhin[5]推导的公式具有最广泛的适用范围，这是由于该公式的推导是基于机理模型。但需要注意到，其预测结果在各个工况下相比其余预测模型，均与试验值偏差较大，在高喷射压力条件下这一偏差尤为明显。在中低喷射压力下，这一模型的预测结果有所改善。

图2 各贯穿距经验公式适用喷射压力范围

曾伟等[4]得到的无量纲准则数经验公式在喷射压力位于或略高于汽油机工况时预测效果较好，但在柴油机工况下模型预测结果会出现明显的偏差。表4列出了各数据集柴油机工况下的准则数值，用以确认该数据集是否位于适用范围。该经验公式的偏差主要由韦伯数的偏离导致。当喷射压力达到柴油机范围，喷射速度明显提升，惯性力影响将高于表面张力作用，喷雾动量将显著增强，使得贯穿距明显增加。

表4 各数据集无量纲准则数总结

Naber[2]，Payri[3]，Hiroyasu[7]等得到的结果在全工况具有较高的相似度，在汽油机工作频段均具有较为明显的偏差，而在柴油机工况下的偏差较小(见图1)。图3示出了高喷射压力工况下的预测情况。明显可见，试验数据与预测数据均均匀分布于45°线，由此进一步验证了上述三个公式在高喷射压力下预测的准确性。

图3 高喷射压力工况贯穿距经验公式数据与实测数据对比

由上述对比分析可知，在汽油机工况下，除曾伟[4]等提出的无量纲准则数公式外，其余预测模型均会产生较大的误差，但在柴油机工况下结果则相反。因此，在选择经验公式时，应该将实际工况列入考虑范围。

2.2.2 喷雾锥角结果对比

图4示出了喷雾锥角经验公式预测结果与试验测量结果对比。Siebers[6]，Hiroyasu[7]所得的预测值在全喷射压力工况下具有较高的相似度，两者在喷射压力较低的汽油机工况下会产生较为明显的偏差，当喷射压力极高时，两者的预测结果较为精确。图5示出了不同经验模型的适用喷射压力范围。Siebers[6]，Hiroyasu[7]经验公式覆盖了高压区域，而Reitz[8]得到的公式覆盖低压区域。

图4 喷雾锥角试验数据与经验公式预测结果对比

图5 各喷雾锥角经验公式适用喷射压力范围

考虑到各公式的适用范围，Wakuri[1]与Reitz[8]所得的经验公式能够在低喷射压力范围得到较好的预测结果，在汽油机工作范围，两者均表现出较好的预测结果，而Reitz模型的预测结果相比而言更佳。当喷射压力极高时，两者的预测结果均出现较明显的误差。

曾伟[4]无量纲准则数锥角预测模型在汽油机工作工况下具有极高的精确度，但在柴油机工作频段预测效果较差。表5列举了各工况下关键无量纲参数的取值，以及该工况是否可以使用无量纲准则数公式。由表5可见，具有较大误差的预测结果均位于适用范围之外，这一现象进一步证明了这一经验公式在适用范围内预测的准确性。

表5 各数据集无量纲准则数总结

由上述分析可知，曾伟[4]与Reitz[8]经验模型在汽油机工况下能够较为准确地预测喷雾锥角。只有这两条经验公式考虑了雷诺数、韦伯数对喷雾形态的影响， 而其余公式则主要考虑喷嘴参数、气液相密度比等参数的影响。因此，曾伟[4]，Reitz[8]推导的经验公式更适用于汽油机喷雾锥角预测。根据图4可知，Siebers[6]得到的经验公式更适于柴油机喷雾锥角的预测。

3 结束语

本研究对预测喷雾形态的经验公式进行了总结，并分析了其理论缺陷与适用范围。从已有文献中挖掘出多种工况、喷嘴结构下的喷雾形态数据，与经验公式进行匹配对比，发现主流喷雾形态预测经验公式由于其理论缺陷和适用范围的局限性，公式之间的相互印证性不佳。本研究对各经验公式之间的差异进行了系统性评估，得到如下结论：对喷雾贯穿距预测而言，曾伟推导的无量纲准则数经验公式可以较好地适用于汽油机工况，而Payri，Naber，Hiroyasu等得到的经验公式适用于柴油机工况；对喷雾锥角预测而言，曾伟无量纲准则公式能够对汽油机喷雾做出较为准确的预测，而Siebers公式可以对柴油机喷雾准确预测。