压气机叶轮失效转速预测方法研究
景国玺,张文凯,张军海,刘欣源,花琳
(1.河北工业大学机械工程学院,天津 300401;2.天津市新能源汽车动力传动与安全技术重点实验室,天津 300400;3.中国北方发动机研究所(天津)柴油机增压技术重点实验室,天津 300400)
为满足日益严格的环保要求和高功率要求,涡轮增压技术在20世纪被首次提出。涡轮增压技术可以大幅度提高内燃机的性能,减少有害气体的排放,对提高内燃机的性能意义重大[1]。由于汽车运行工况复杂多变,增压器转速有时会超过标定转速,而且高功率柴油机要求不断提高增压比,这些都对增压器的涡轮和叶轮的强度及疲劳性能提出更高的要求,而涡轮和叶轮的工作可靠性是增压器设计的难点[2]。
在实际工作过程中涡轮和叶轮受到多种载荷的耦合作用,包括螺栓装配载荷、热载荷、离心力载荷和气动载荷,其中离心力载荷对涡轮和叶轮的应力及变形影响最大[3-4]。北方交通大学的朱宝山和侯炳麟等[5]针对增压器超转速下的叶轮进行弹塑性分析,为超转速加工工艺规程提供了定量依据。浙江大学的陆君毅和吴秀仁[6]通过叶轮的超转速破坏性试验,对高强度钢制闭式叶轮在离心力场下的破坏过程进行了试验研究。浙江大学的吴秀仁[7]提出了一种模块式增压器叶轮立式超转速试验机,具有试验转速、质量、外形尺寸等参数范围宽的特点,理论上最高转速可达120 000 r/min。中航工业发动机设计研究所的万江艳和周柏卓[8]建立了与材料延伸率相关的轮盘弹塑性破裂准则,采用非线性有限元法对变厚度轮盘破裂试验件的破裂转速进行了预测,试验对比效果良好。王浩然[9]进一步使用 Tresca 屈服准则下的整体塑性失稳破坏准则,准确预测了 GH4169 材料复杂几何形状模拟盘的破裂转速,揭示了整体塑性失稳破坏准则下屈服准则的选用对于轮盘破裂转速预测的影响。Hassani等[10]采用了HAM方法和有限元法,得到了弹塑性载荷作用下非均匀厚度和材料特性的旋转圆盘的应力应变分布。Ranjan和 Vinayak等[11]采用有限元方法对典型变厚度燃气轮机盘进行了不同转速下的弹性和弹塑性分析,得到了复杂载荷条件下的爆炸裕度。
目前多数研究都是针对航空发动机涡轮盘进行破裂转速预测。根据GJB 241A—2010《航空涡轮喷气和涡轮风扇发动机通用规范》,当轮盘承受最大温度梯度和最高工作温度时,轮盘的设计破裂转速不低于最高允许稳态转速的122%,但对于车用发动机压气机叶轮,叶轮的破裂转速要求在标定转速的1.4倍以上。考虑到航空发动机涡轮盘与压气机叶轮结构和材料特性的差异,涡轮盘预测破裂转速的方法不能完全应用于压气机叶轮。随着增压技术的广泛应用,压气机叶轮在超转速工况下的安全成为亟待解决的问题,也是影响压气机正常工作的关键问题之一,对压气机叶轮的转速破坏研究分析具有重要的意义。
本研究针对某型压气机叶轮,进行弹塑性失效分析,提出3种预测失效转速的方法。针对叶轮材料锻铝合金2A70进行拉伸试验,获得材料的各项性能参数。对压气机叶轮进行超转速破坏试验,将试验叶轮失效转速与仿真模拟预测失效转速进行对比,验证3种预测失效转速方法的准确性。
1 叶轮超转速理论分析
大量的强度破坏现象和试验证明,无论应力状态多么复杂,在常温、静载荷的条件下,材料失效的形式主要有两种,分别为脆性断裂和塑性屈服[12]。本研究中叶轮材料为锻铝合金,在屈服极限之前应力与应变成正比,在屈服极限之后出现塑性变形。选择合适的强度破坏理论,是预测叶轮最大失效转速的关键。
1.1 Mises应力理论
对于均质脆性材料,第一强度理论与试验结果吻合,即无论材料处于什么应力状态,只要危险点处的最大拉应力σ1达到材料单向拉伸时的断裂真应力σ,材料就会发生脆性断裂,即材料的破坏条件为
σ1=σ。
(1)
对于复杂构件来说,该理论未考虑其他两个主应力的影响,因此德国的R. Von Mises 在 1931 年提出Mises应力。该应力考虑中间应力的影响,不需要知道3个主应力的方向。对于韧性金属,该条件非常接近于试验情况。Mises应力计算公式为
(2)
式中:σx,σy和σz为3个方向的正应力;τxy,τyz和τzx为3个方向的剪应力。
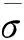
1.2 主塑性应变理论
对于脆性断裂来说,第二强度理论与试验吻合较好,即无论材料处于什么应力状态,只要危险点处的最大拉应变ε1达到材料的单向拉伸断裂时的拉应变极限值ε1u,材料就发生脆性断裂,即材料破坏条件为
ε1=ε1u。
(3)
对于受力情况复杂的构件来说,应变可分为弹性应变和塑性应变,弹性应变在应力消失后可恢复[13],因此提出主塑性应变理论:当叶轮的转速增加时,叶轮任一点的主塑性应变εp1达到材料的断裂塑性应变εp时,叶轮发生破坏,这时的转速就是叶轮的失效转速。
1.3 等效塑性应变能理论
超转速过程中任一点的应变ε都可表示为弹性应变εe和塑性应变εp之和,即
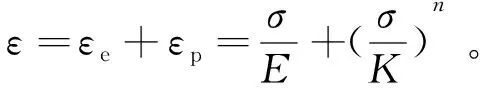
(4)
式中:E为弹性模量;K为强度系数;n为应变强化指数。叶轮超转速的过程中应力应变关系符合著名的Remberg-Osgood弹塑性模型。若变形过程中不考虑其他能量对该系统的影响,外力的变化缓慢,则结构中的应变能近似等于外力对该系统做的功,即应力应变曲线下包含的面积可用下式表示[14]:
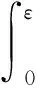
(5)
式中:ε为应变;σ(ε)为应力关于应变的函数。
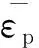
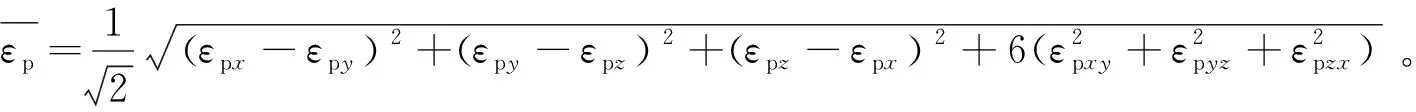
(6)
式中:εpx,εpy和εpz为3个方向的塑性正应变;εpxy,εpyz和εpzx为3个方向的塑性剪应变。

(7)
式中:εp为塑性应变;σ(εp)为应力关于塑性应变的函数。
2 叶轮超转速破坏仿真模拟研究
2.1 有限元模型
压气机模型(见图1)由螺母、叶轮、轴封套、甩油盘、止推、间隔套和转轴组成,压气机叶轮、轴承套等零部件通过螺母与转轴固定。模型采用四面体二阶单元,局部进行细化处理,叶轮材料为锻铝合金2A70。
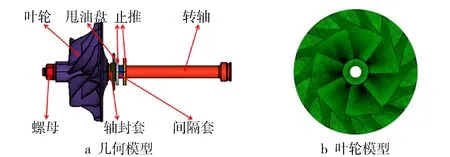
图1 压气机模型
2.2 叶轮材料的力学性能参数
叶轮在工作过程中的受力情况十分复杂,对叶轮的强度等性能提出了很高的要求。考虑到叶轮在超转速过程中发生塑性变形,仅采用弹性模型得出的结果并不可靠,无法做出确切的失效分析,其结果将使模型不能充分发挥材料的全部承载能力[15],因此采用弹塑性模型。根据GB/T 228.1—2010《金属材料 拉伸试验 第1部分:室温试验方法》进行叶轮试样的室温拉伸试验,拉伸试样尺寸如图2所示,试验在MTS电子万能试验机上进行。测试试样(见图3)为3个,试样编号为W1-L-1,W1-L-2,W1-L-3。试验温度为25 ℃,试验时加载应变速率为0.000 25/s。

图2 拉伸试样尺寸

图3 室温拉伸试验试样
图4示出2A70材料的工程应力应变曲线,可以看出,拉伸变形后期存在轻微颈缩现象,导致在工程应力应变曲线中出现应力下降的情况。材料在屈服点以后,分子的流动导致试样的横截面面积A显著减小,材料实际承受的应力要大于按原始的横截面面积计算的工程应力。所加载荷应等于真实应力与实际面积的乘积。经过数据处理,得到真实应力应变曲线,如图5所示。室温下叶轮材料2A70的性能参数见表1。
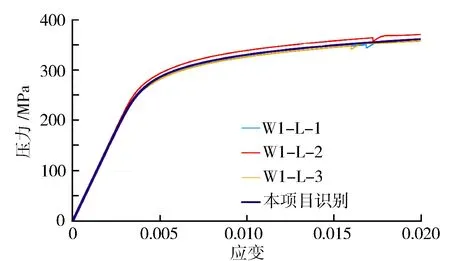
图5 2A70材料真应力应变曲线

表1 2A70材料参数
2.3 叶轮载荷分析和约束条件
参考叶轮在超转速试验的工作过程,叶轮主要受到螺栓预紧力和离心力的作用。根据螺母的形状尺寸以及扭紧力矩62 N·m,可计算出离心力约为38 000 N。离心力载荷以角速度的形式施加在叶轮上,随着转速的增加,离心力不断增大,角速度也不断增大。转速的变化过程按照叶轮超转速破坏试验规范进行,如图6所示。
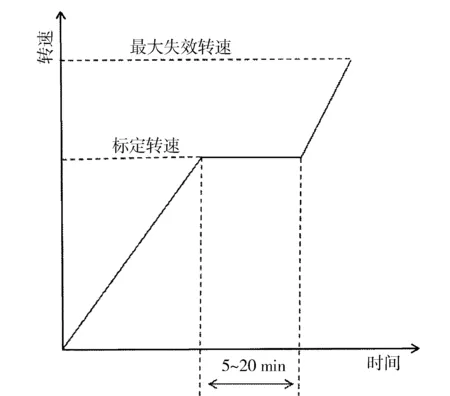
图6 叶轮升速规范
根据叶轮的超转速试验进行约束,如图7和图8所示,对位置1约束Z方向的移动,对位置2约束X和Y方向的移动,对位置3施加螺栓预紧力。

图7 压气机约束位置
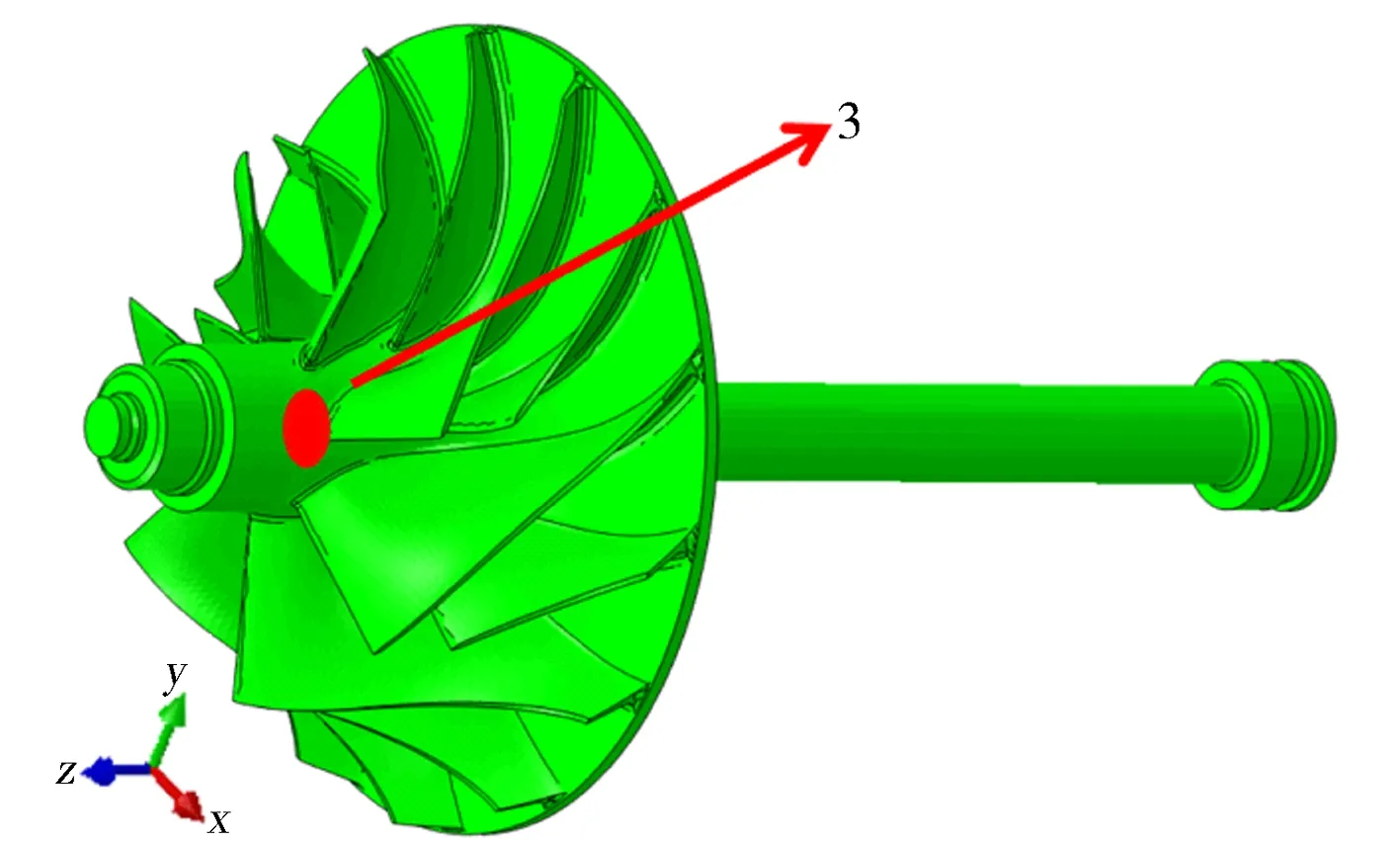
图8 压气机螺栓预紧面
2.4 叶轮载荷特性分析
利用abaqus软件,进行压气机叶轮的有限元分析。在仿真分析计算超转速工况时,首先需要施加螺栓预紧载荷,仅考虑螺栓装配载荷时的应力分布云图如图9所示。Mises应力为叶轮的等效应力,主应力图可用来判断局部的拉伸压缩情况。当主应力为正时,呈拉伸状态,当主应力为负时,呈压缩状态。
叶轮主要受压应力,最大压应力为269 MPa左右,出现在叶轮靠近螺母一端的端面上,是由于螺栓预紧力在此处存在应力集中现象,但叶轮未发生塑性变形。

图9 螺栓预紧力载荷下的应力分布
图10示出不同转速下叶轮的Mises应力分布云图,图11示出不同转速下叶轮的主应力分布云图,可以看出,在标定转速90 200 r/min下,叶轮的最大拉应力为327 MPa左右,出现在叶片根部区域。叶片工作面的叶根处主要受拉应力,另一侧叶根处主要承受压应力。由于叶片根部设计相对较薄,因此出现高应力区[16]。

图10 不同转速下叶轮Mises应力分布
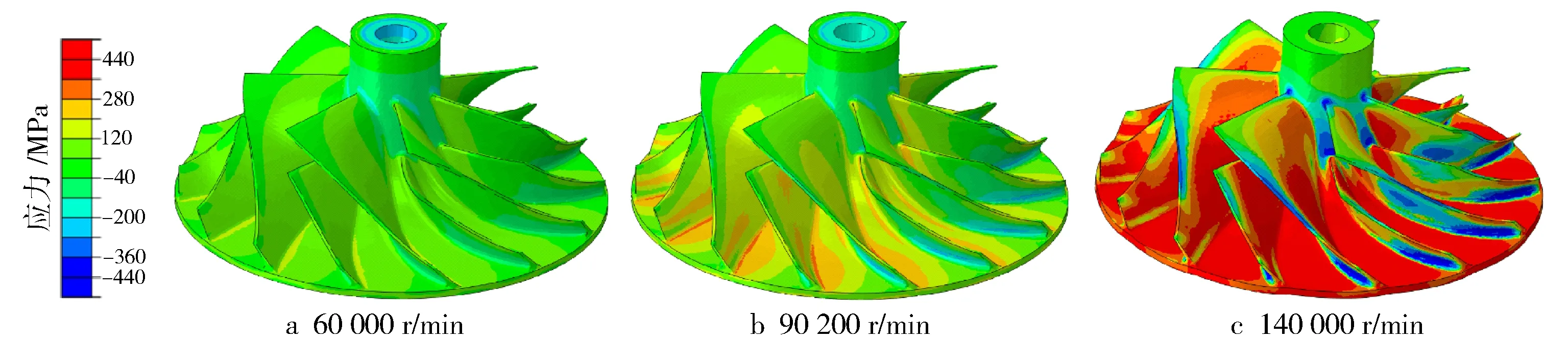
图11 不同转速下叶轮主应力分布
3 叶轮超转速破坏试验
3.1 试验说明
涡轮增压器叶轮超转速破坏试验的目的在于评估增压器在超转速条件下的工作可靠性,同时可作为确定增压器最高破坏转速的依据。在结构设计不变的前提下,叶轮超转速破坏试验结果反映叶轮承受离心力的能力。大量的工程实践证明,利用叶轮的超转速破坏试验可以检查叶轮设计的可靠性和铸造质量,对叶轮的设计和应用都具有重要的意义。
增压器的超转速破坏试验采用外气源热吹的方式进行,在有防护装置的专用试验台架(见图12)上进行。在试验开始时,叶轮加速到标定转速,稳定运行5~20 min,然后继续增加叶轮的转速,直到叶轮发生断裂破坏,记录叶轮发生失效的转速,为增压器压气机叶轮的仿真模拟提供最大转速依据。

图12 叶轮超转速试验台示意
3.2 叶轮的超转速破坏试验结果分析

在超转速试验台上完成叶轮的超转速试验,当压气机叶轮飞散时,实际转速约为126 700 r/min,约为标定转速的1.4倍,满足基本设计要求。
4 叶轮失效转速预测方法
在叶轮转速增加时,叶轮内部的缺陷或者叶轮表面的加工问题,都会造成应力集中并产生裂纹源。在试验时,叶轮裂纹拓展,直至断裂。但在仿真时,采用不同的叶轮失效转速预测方法,往往会得出不同的结果。
本研究采用了3种预测失效转速的方法,分别基于叶轮的Mises应力、主塑性应变和等效塑性应变能。方法一基于叶轮的Mises应力,比较通过拉伸试验得到的材料断裂真应力与叶轮仿真模拟得到的Mises应力,找出叶轮的失效转速。方法二基于主塑性应变,为试验试样断裂时发生的主塑性应变。方法三基于等效塑性应变能,即物体变形过程中储存在物体内部的势能。根据超转速试验易开裂的位置,结合有限元仿真的结果,在叶轮上确定14个典型的观察点,各观察点的位置如图13所示。由于叶轮是轴对称模型,因此选择的观察点集中于一对大、小叶片和轮盘上,根据Mises应力、主塑性应变出现的位置和结构特征来确定。
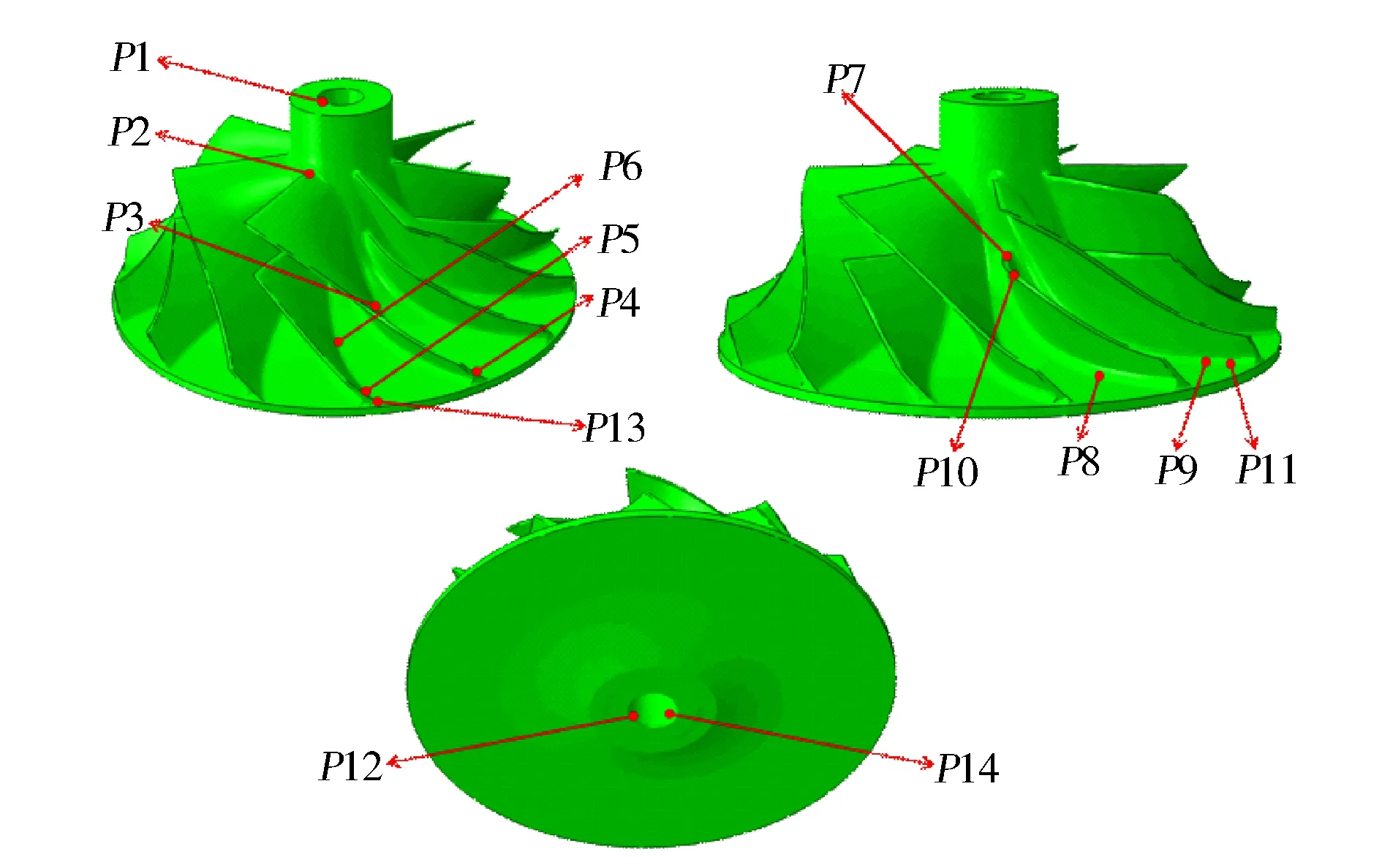
图13 观察点示意
4.1 基于Mises应力的失效转速预测方法
通过材料的拉伸压缩试验,可以得出材料在室温下的断裂真应力为437 MPa。根据Mises应力理论,当叶轮上任一点的Mises应力大于437 MPa时,叶轮发生破坏,此时对应的叶轮转速即为叶轮失效转速。由图14可知,叶轮上P5点的Mises应力首先达到437 MPa,开裂位置出现在小叶片叶根处。此时叶轮的转速131 975 r/min即为失效转速,是标定转速的1.46倍。

图14 不同观察点Mises应力随转速的变化曲线
4.2 基于主塑性应变的失效转速预测方法
通过材料的拉伸压缩试验,可以得出材料在室温下的断裂塑性应变为0.127。根据主塑性应变理论,当叶轮上任一点的主塑性应变大于0.127时,叶轮发生破坏。由图15可知,叶轮上P13点的主塑性应变首先达到0.127,开裂位置出现在小叶片叶根处。此时叶轮的转速137 815 r/min即为叶轮的失效转速,约为标定转速的1.53倍。
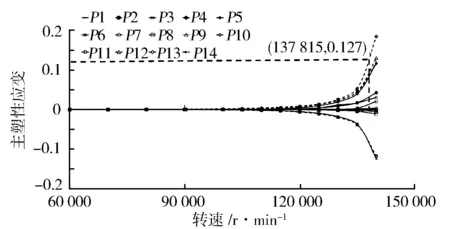
图15 不同观察点主塑性应变随转速变化曲线
4.3 基于等效塑性应变能的失效转速预测方法
通过材料的拉伸试验,可以得出在室温下材料破坏时的塑性应变能为51.64 J。根据叶轮超转速过程中的等效塑性应变能理论,当叶轮任一点的等效塑性应变能大于51.64 J时,叶轮发生破坏。由图16可知,叶轮上P13点的等效塑性应变能首先达到材料破坏时的塑性应变能,开裂位置出现在小叶片叶根处。此时叶轮的转速为135 455 r/min,即135 455 r/min为失效转速,约为标定转速的1.5倍。
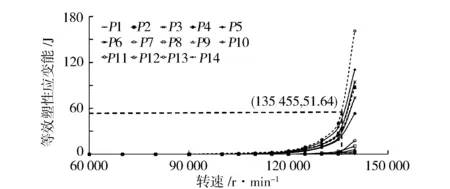
图16 不同观察点等效塑性应变能随转速的变化
4.4 叶轮失效转速预测方法分析
经过试验验证与仿真的对比分析可知,利用Mises应力预测失效转速的方法相对试验偏差相对较小,为4.2%,Mises应力值可从仿真中直接得到。利用等效塑性应变能计算预测失效转速的方法偏差相对较大,为6.9%。利用主塑性应变预测失效转速的方法相对试验偏差最大,为8.8%,可从仿真结果中直接读取。
从对比结果来看,三种方法预测出的失效转速均大于试验值。出现这种现象的原因有两个:一是叶轮表面存在用于改善叶轮气动性能的纹路,叶轮表面较粗糙,而叶轮材料拉伸试验中使用的拉伸试样较光滑,这是仿真得出的叶轮失效转速大于试验值的主要原因;二是由于试验成本的限制,只进行了一个叶轮的超转速试验,超转速试验得出的失效转速具有一定的分散性,试验失效转速结果理论上应为一定范围区间的分布,因此仿真给出的失效转速与试验值存在一定的偏差。
本研究采用的3种方法借鉴了航空发动机涡轮盘的破裂准则,并在此基础上进行深入研究。从预测结果来看,3种方法同样适用于车用发动机压气机叶轮的失效转速预测,因此模型具有一定的普适性,但对于塑性较好的铝合金材料,推荐采用Mises应力作为超转速失效判据。
5 结论
a) 叶轮在超转速工况下主要受到螺栓预紧力和离心力的影响,其中离心力的影响最大;最大应力出现在叶片根部区域;
b) 在超转速试验台完成压气机叶轮的超转速试验,叶轮的破坏转速为126 700 r/min,为标定转速的1.4倍,符合叶轮强度的安全标准;
c) 提出3种预测叶轮失效转速的方法,分别基于Mises应力、主塑性应变和等效塑性应变能,综合比较3种方法,基于Mises应力预测失效转速的方法相对试验偏差最小,为4.2%;3种方法预测的破坏位置均在小叶片叶根处,预测的最大转速均偏大。

