考虑时变备用需求的含大规模风电电力系统机组组合滚动优化

桂前进 黄向前 麦 立 徐瑞翔

考虑时变备用需求的含大规模风电电力系统机组组合滚动优化

桂前进1黄向前1麦 立2徐瑞翔1

（1. 国网安徽省电力公司安庆供电公司，安徽 安庆 246003； 2. 国网安徽省电力有限公司，合肥 230022）

风电的波动性及难以预测的特性给电力系统安全、经济调度带来了困难。含风电电力系统机组组合需安排火电预留足够的旋转备用容量，以减小风电波动和预测误差对电力系统的影响。本文针对风电预测误差的强时变特性，提出考虑时变备用需求的含大规模风电电力系统机组组合滚动优化模型，该模型充分考虑风电预测误差的时变特性，优化系统机组组合滚动运行方案。算例分析证明了本文模型的有效性和可行性，分析表明本文模型能够满足系统时变备用需求，保证系统不同时间尺度的运行安全性和经济性。

风电不确定性；时变特性；滚动优化；线性规划

0 引言

在“30·60”双碳目标要求下，未来电力系统将遵循“清洁化、综合化、智慧化”的创新趋势发展，并将促进新能源发电进一步发展[1]。风电作为主要的新能源发电形式，其波动性和间歇性给电力系统安全运行带来严峻挑战[2]。为了应对风电不确定性，含大规模风电并网电力系统机组组合需安排火电预留足够的旋转备用容量，以保证系统运行安全[3]。

预留旋转备用容量增加会提升系统运行安全性，但会增加运行成本，降低运行经济性。因此，含大规模风电电力系统机组组合应力求运行经济性与安全性的平衡[4]。

准确的风速预测技术对旋转备用容量的确定具有重要作用。更高的预测精度意味着更低的旋转备用需求[3]。虽然风速预测技术已取得长足发展，但风速自身的随机性使风速预测不可避免地具有较大的预测误差。风速预测的准确度随时间尺度延长逐渐降低，且预测误差的概率分布具有时变特性[5]。因此，含风电电力系统机组组合应针对不同时间尺度调度计划，充分考虑风速预测误差的时变特性，以在保证运行安全的前提下，降低系统运行成本。

对于含风电电力系统机组组合的研究，根据风电不确定性处理方法主要分为：确定性方法[3, 6]、模糊方法[7-8]、随机方法[9-10]。确定性方法通过风能的历史数据确定系统补偿风电出力的额外旋转备用需求。文献[3]利用统计方法，对历史风速数据和预测数据做统计分析，根据置信水平动态确定系统备用容量。模糊方法采用模糊集表征风电出力不确定性，通过求解模糊规划进行机组组合[8]。随机方法利用概率分布表征风能或预测误差，能更加准确地处理风能不确定性，但计算量较大[11]。

关于含风电电力系统机组组合的研究已有很多文献，但现有研究仅针对单一时间尺度分析风电预测误差统计特性，确定旋转备用需求，未研究风电预测误差的时变概率特性及时变的旋转备用需求，无法应用于电力系统机组组合滚动优化，且无法保证系统不同时间尺度的运行安全性和经济性。

鉴于此，本文针对风电功率预测误差的时变特性，对考虑时变备用需求的含大规模风电电力系统机组组合滚动优化方法展开研究。主要创新点如下：①分析风电预测误差的时变概率特性，基于机会约束方法确定含大规模风电并网电力系统时变旋转备用容量需求；②考虑时变旋转备用需求，基于混合整数线性（mixed integer linear, MIL）方法，建立含大规模风电电力系统机组组合滚动优化模型。

本文模型能够充分考虑风电功率预测误差的时变特性，确定含大规模风电电力系统时变的旋转备用容量需求，并根据电力系统多时间尺度机组组合优化模型，确定含高比例风电电力系统机组组合滚动运行方案，保证系统不同时间尺度的运行安全性和经济性。基于混合整数线性规划建模能有效降低模型的计算复杂性，为大规模系统应用提供基础。

1 风电预测误差时变概率特性分析及时变旋转备用容量确定

1.1 风电预测误差时变概率特性分析

风速受气候环境等因素的影响，具有较强的随机性和波动性，准确预测风速和风电功率困难较大。风速预测误差的概率分布特性与预测模型、预测时长等均有关。分析历史风速数据和预测结果可以得到风电功率预测误差的分布特性[12]，进而通过风电机组的风电转换模型，可以得到风电功率的预测分布统计特性。

根据对风速预测结果和历史风速数据的分析，风速预测误差可近似认为服从正态分布[13]，即

式中：为风速预测误差；和分别为预测误差的期望值和标准差。

风电转换关系近似表示为[14]

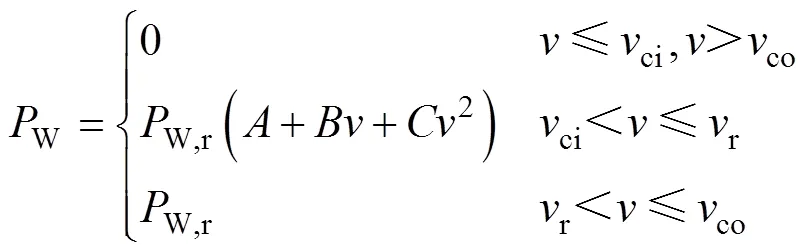
式中：W为风电机组出力；W,r为风电机组额定容量；ci、r和co分别为风电机组切入、额定和切出风速；、、为风电转换模型的系数[15]。

根据风速的预测误差分布结合风电机组的风电转换模型，即可得到风电出力的预测误差分布的概率特性。

风速的预测效果一般会随着预测时间的延长逐渐变差[5]，并使预测误差的概率分布发生变化，表现为时变概率特性。风速或风电功率的预测可以分为日前预测和短期（或超短期）预测[16]。日前风速预测通常采用数值天气预报（numerical weather prediction, NWP）方法，日前风速预测误差由NWP技术决定。短期（超短期）风速预测一般采用统计学方法，预测误差在很大程度上受预测时间影响。

1.2 基于风速预测误差时变概率特性的系统时变备用容量确定方法

含大规模风电电力系统机组组合中旋转备用容量需求主要取决于风电功率预测误差。充分分析各时间尺度预测误差的时变分布特性，基于风电预测误差时变概率特性，确定系统各时间尺度备用容量需求。采用滚动的优化方法，考虑系统时变备用容量需求，及时更改运行方案，可以保证系统运行安全性和经济性。

含大规模风电电力系统调度示意图如图1所示，日前机组组合即安排火电机组和预测的风电满足次日预测负荷。由于风电和负荷预测误差，日前机组组合需预留足够的旋转备用容量，保证系统运行安全。

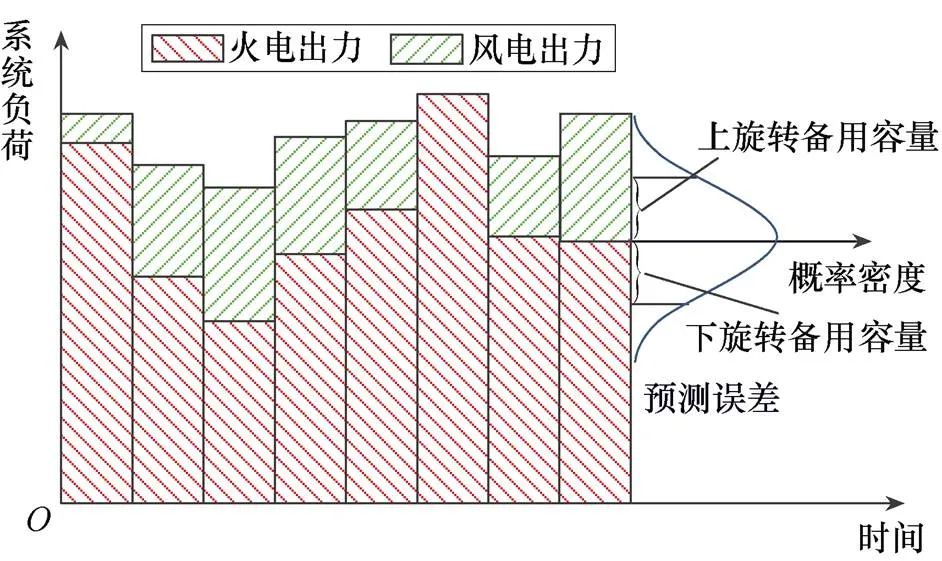
图1 含大规模风电电力系统调度示意图

旋转备用容量分为上旋转备用容量和下旋转备用容量。传统（无新能源）电力系统中，负荷预测误差相对较小，而且电源基本为可调节的火电、水电等常规机组，机组向下调节容量较为充裕。因此，仅需设置因设备故障和负荷预测误差所需的基本向上旋转备用容量。针对大规模风电的不确定性，本文模型在原有的旋转备用约束的基础上增加因风电并网而需要的额外向上和向下旋转备用需求[6]。

本文基本旋转备用容量根据系统容量取固定 值[6]。对于额外旋转备用容量，根据风电预测误差时变概率特性，采用机会约束方法，确定各时间尺度的额外旋转备用需求。系统时变备用容量需满足的约束为

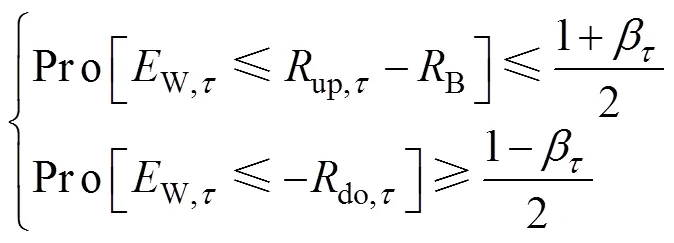
根据机会约束的方法[17]可将系统时变备用容量约束转化为确定形式，即

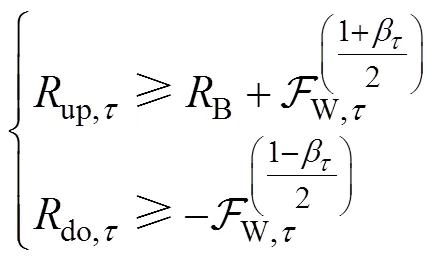
2 考虑时变备用需求的含风电电力系统机组组合滚动优化模型

本文基于风电功率预测误差的时变特性，采用两阶段滚动优化方法进行机组组合优化。考虑时变备用需求机组组合滚动优化示意图如图2所示，分别对应日前发电计划和滚动发电计划两个时间尺度。第一阶段决策火电起停，第二阶段控制其出力，即日前调度、日内控制的思想。

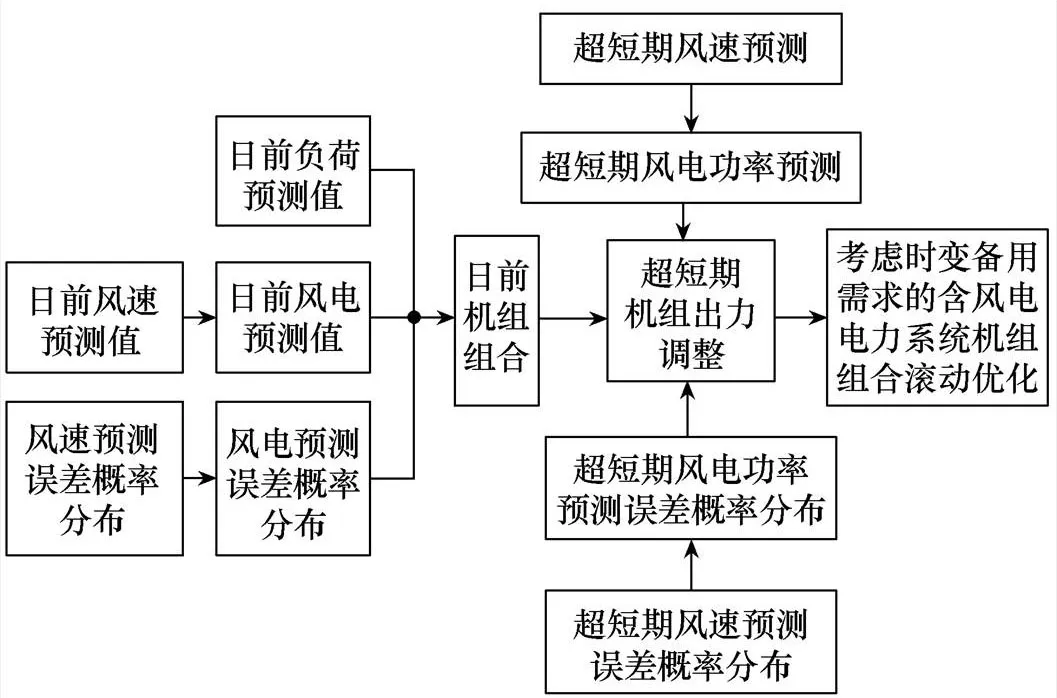
图2 考虑时变备用需求机组组合滚动优化示意图

第一阶段，针对日前风电预测误差概率分布，采用机会约束方法确定旋转备用容量需求，优化次日24h火电机组开停机状态。第一阶段认为次日24h的预测准确度相同，各时段风电功率预测误差服从统一正态分布。第二阶段，根据超短期预测结果，每隔1h对当天剩余时间的机组调度结果按照每15min逐点进行滚动修正。当天剩余时间的风电预测误差分布充分考虑风电功率预测误差时变特性。

第一阶段额外旋转备用容量概率阈值会影响第二阶段系统运行风险。因此，可以提高第一阶段备用容量概率阈值，进而提高系统旋转备用容量，但是这样会造成系统运行成本的增加。因此，在含大规模风电的电力系统机组组合过程中应根据风电预测误差的统计特性，量化系统运行风险，寻求系统运行风险与运行经济性的平衡，在保证运行经济性的过程中可以适当弃一部分风能。

2.1 日前机组组合

1）目标函数

含风电并网电力系统机组组合的目标函数为系统运行总成本最小，包含传统机组的发电成本和机组开机成本，不考虑风电运行成本。目标函数表示为

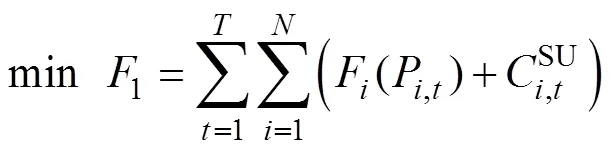
火电机组的燃料成本通常表示为二次形式，为了加快计算速度，本文利用分段线性化进行处 理[18-19]，即

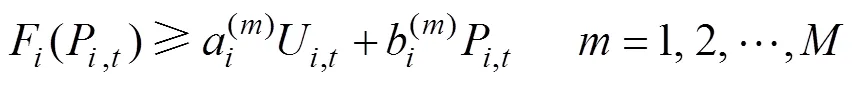
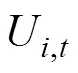
机组开机成本与停机时间相关，按照冷、热起动成本线性化表示为

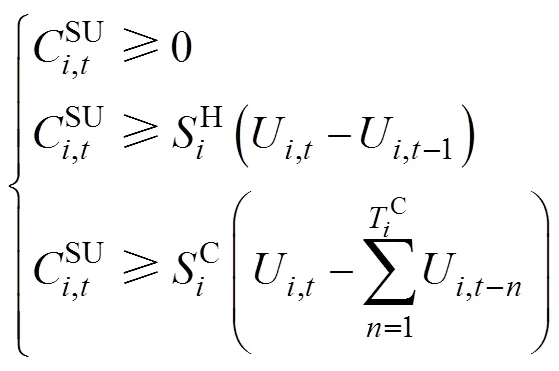
2）约束条件

日前机组组合优化运行问题的约束条件如下。

（1）系统功率平衡约束

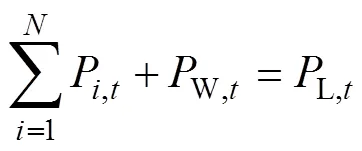
（2）机组运行出力约束

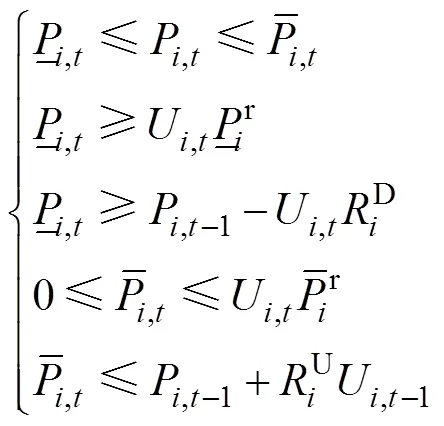
（3）机组最小开停机时间约束

火电机组起停受最小开停机时间限制，本文分成三个时间段建立火电机组起停时间约束。式（11）为最小开机时间约束，只有当火电机组持续开机时间超过其最小开机时间，该机组才能停机。式（12）为最小停机时间约束。

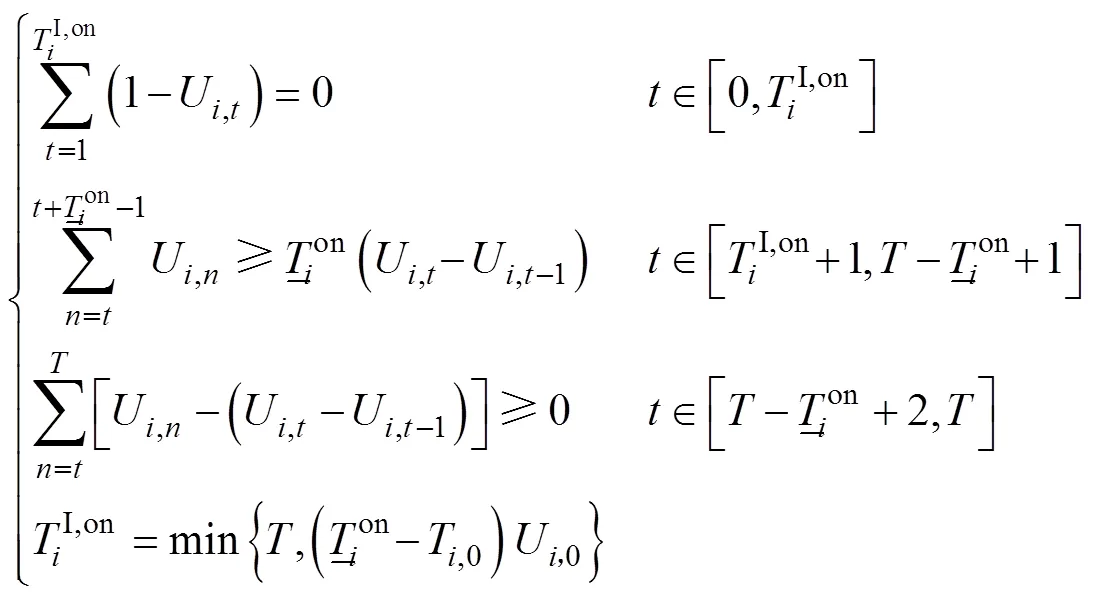
（4）系统旋转备用约束

基本旋转备用容量可以根据系统容量取固定值或负荷的一定比例[6]。本文基于机会约束的方法[19]确定额外旋转备用需求，认为风电功率预测误差服从正态分布，则系统旋转备用约束为

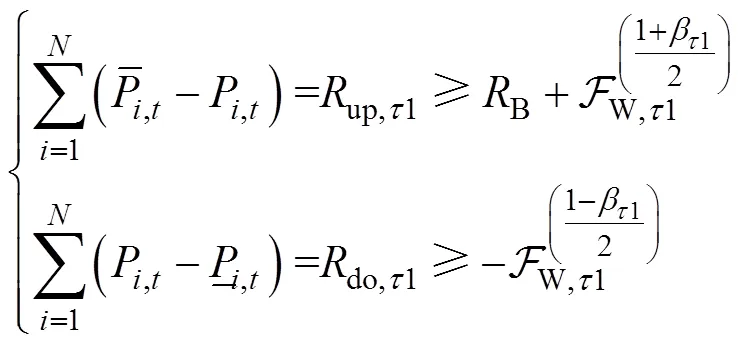
（5）网络潮流约束

基于直流潮流的网络潮流约束为

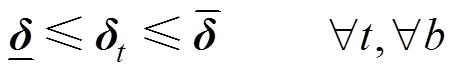
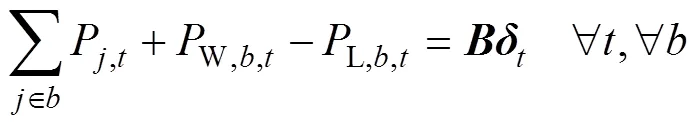
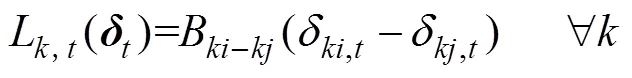
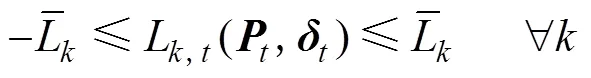
2.2 超短期出力调整

第二阶段根据日前机组组合的机组开停机状态和风电超短期预测结果，每隔1h滚动优化当天剩余时间，按照15min逐点滚动调整机组出力。

考虑到常规火电机组的起、停时间一般较长，通常日内滚动优化过程不允许再改变火电机组的起停计划，因此，本文模型的第二阶段仅根据日前机组组合结果，对剩余时间的机组出力进行滚动调整。

1）目标函数

目标函数为火电机组燃料成本，表示为

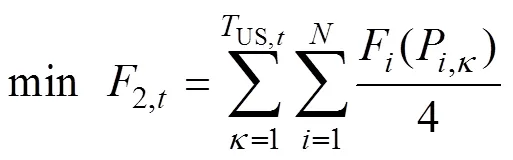
2）约束条件

火电机组超短期出力调整优化模型的约束条件主要考虑功率平衡约束、火电机组出力约束、火电机组状态约束和旋转备用约束，前两种约束与日前机组组合相似，此处不再赘述。以下内容介绍火电机组状态约束和旋转备用约束。

（1）火电机组状态约束

火电机组起停往往需数小时，火电机组超短期出力调整优化中不考虑火电机组的非计划起停，因此火电机组状态需要与日前机组组合结果一致。

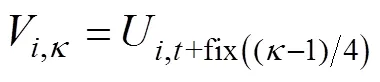
（2）旋转备用约束

因风电功率预测误差分布的时变特性，超短期出力调整中，各个时间段风电功率的分布特性不同，本文假设未来3h每个小时的风电功率预测误差服从同一分布，则旋转备用约束为

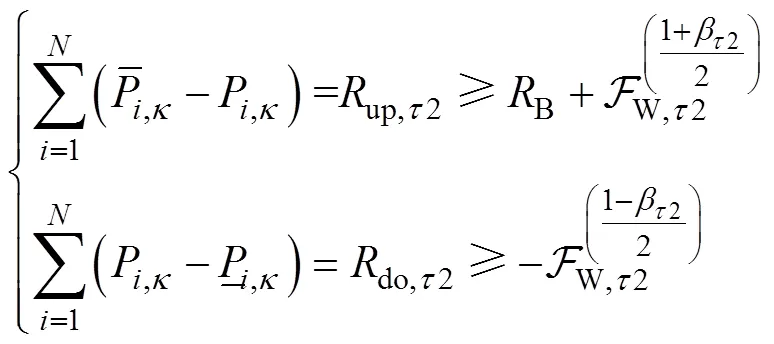
3 算例分析

为了验证本文模型的有效性，以10台机组和600MW风电场构成系统开展算例分析。火电机组参数[20]见表1，系统接线[20]及各机组所在位置如图3所示。利用Matlab编写计算程序，调用GUROBI求解滚动优化模型。

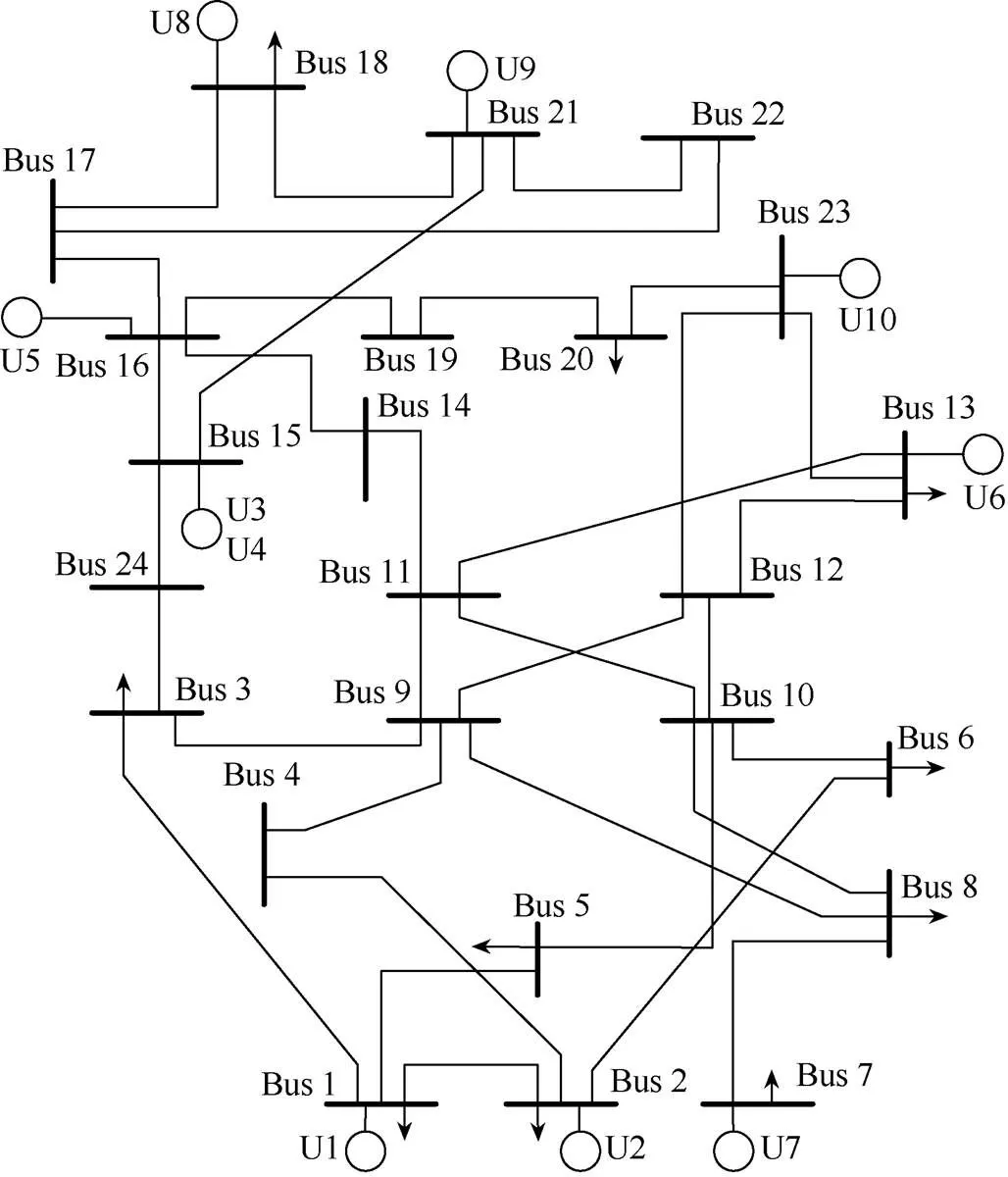
图3 系统接线及各机组所在位置

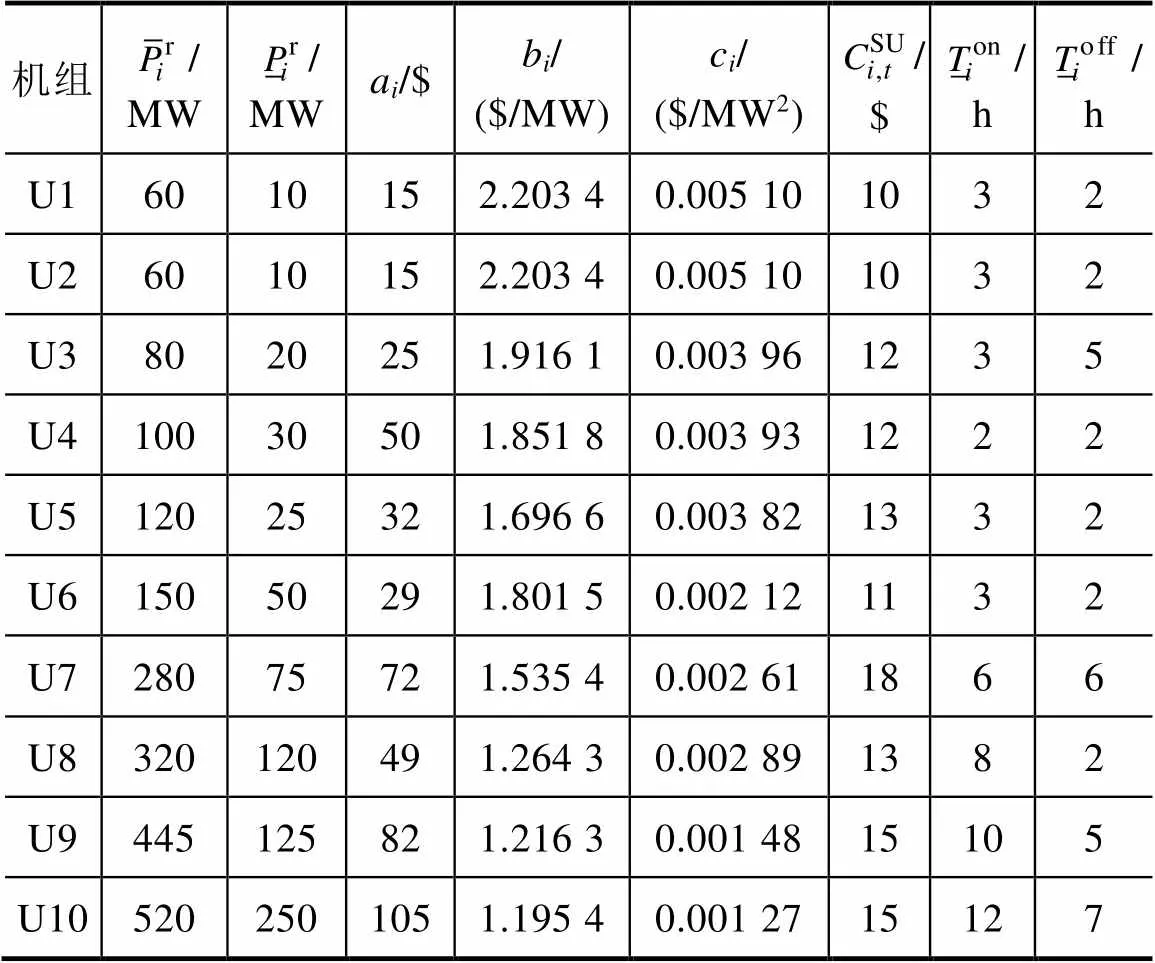
表1 火电机组参数

3.1 模型有效性对比分析

本算例与文献[6]方法进行对比分析。未来一天24h的负荷及风电功率预测值见表2。为了严格验证本文模型有效性，方便与文献[6]结果进行对比，风电数据参考文献[6]均在400MW左右，未能反映风电功率的实际波动情况。文献[6]取基本旋转备用需求为300MW，上、下额外旋转备用容量取为风电功率预测值的20%，本文基于机会约束1取0.8。文献[6]和本文第一阶段日前机组组合结果对比见表3。

比较表3结果可知，两种方法机组起停结果相差不大，只在某些时刻，如9:00、10:00、13:00、17:00、18:00、19:00机组状态不同，说明了本文方法的有效性。本文方法第一阶段总的运行成本较文献[6]有所降低，说明本文在保证风电功率预测准确度的情况下，取额外旋转备用约束的概率阈值1=0.8，较文献[6]取风电功率的固定比例20%能够降低运行成本。

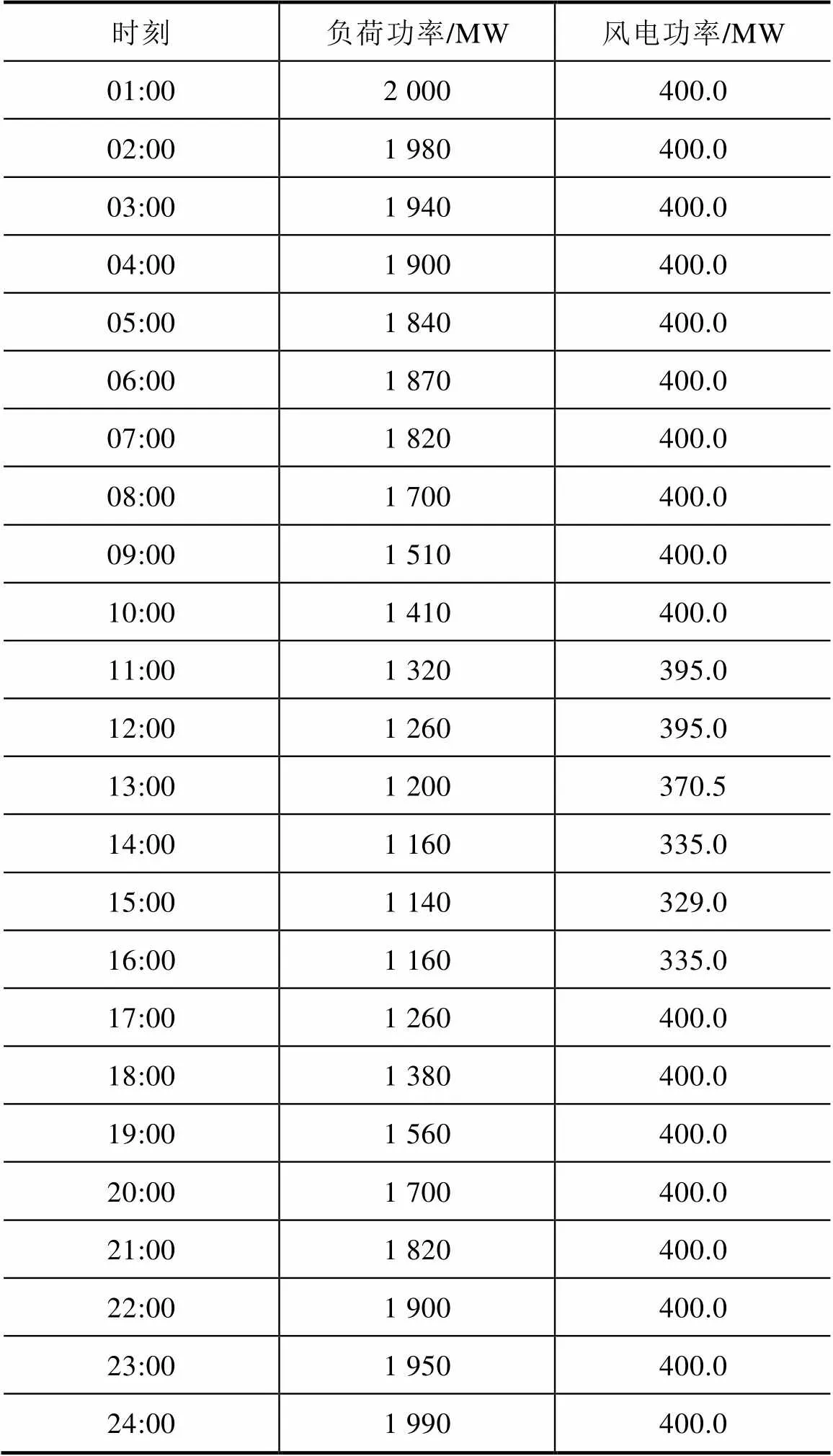
表2 负荷及风电功率预测值

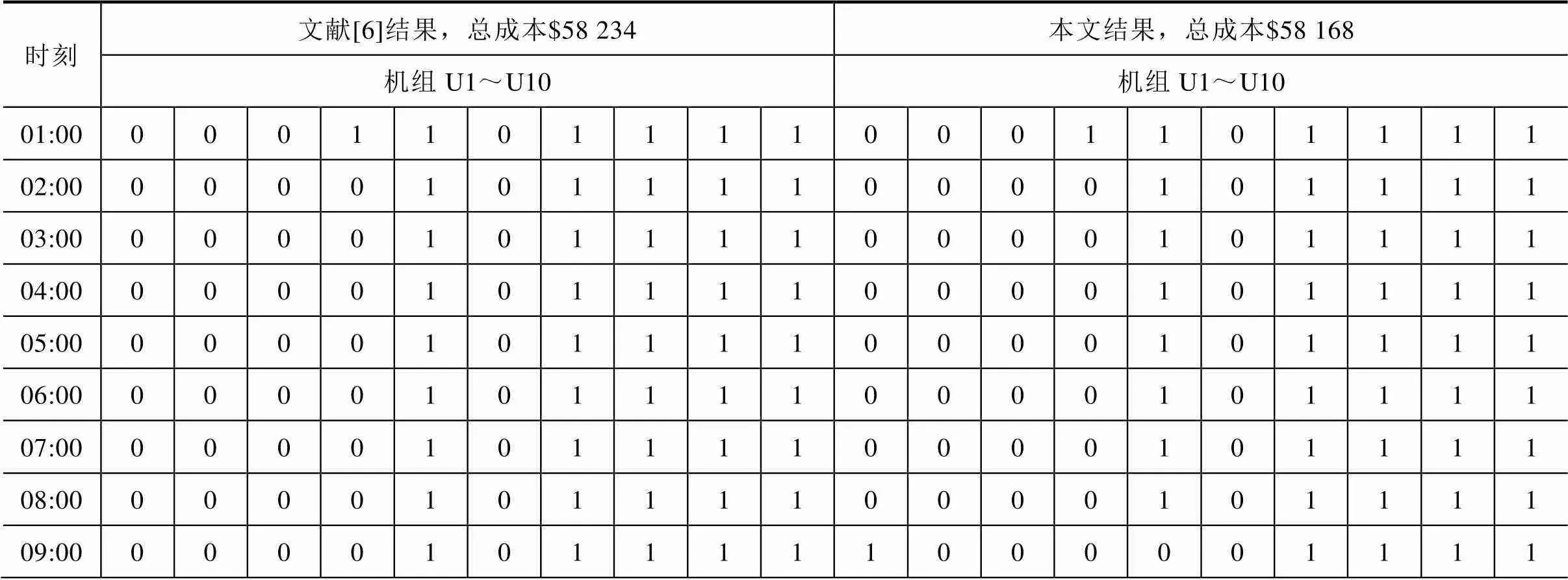
表3 第一阶段日前机组组合结果对比

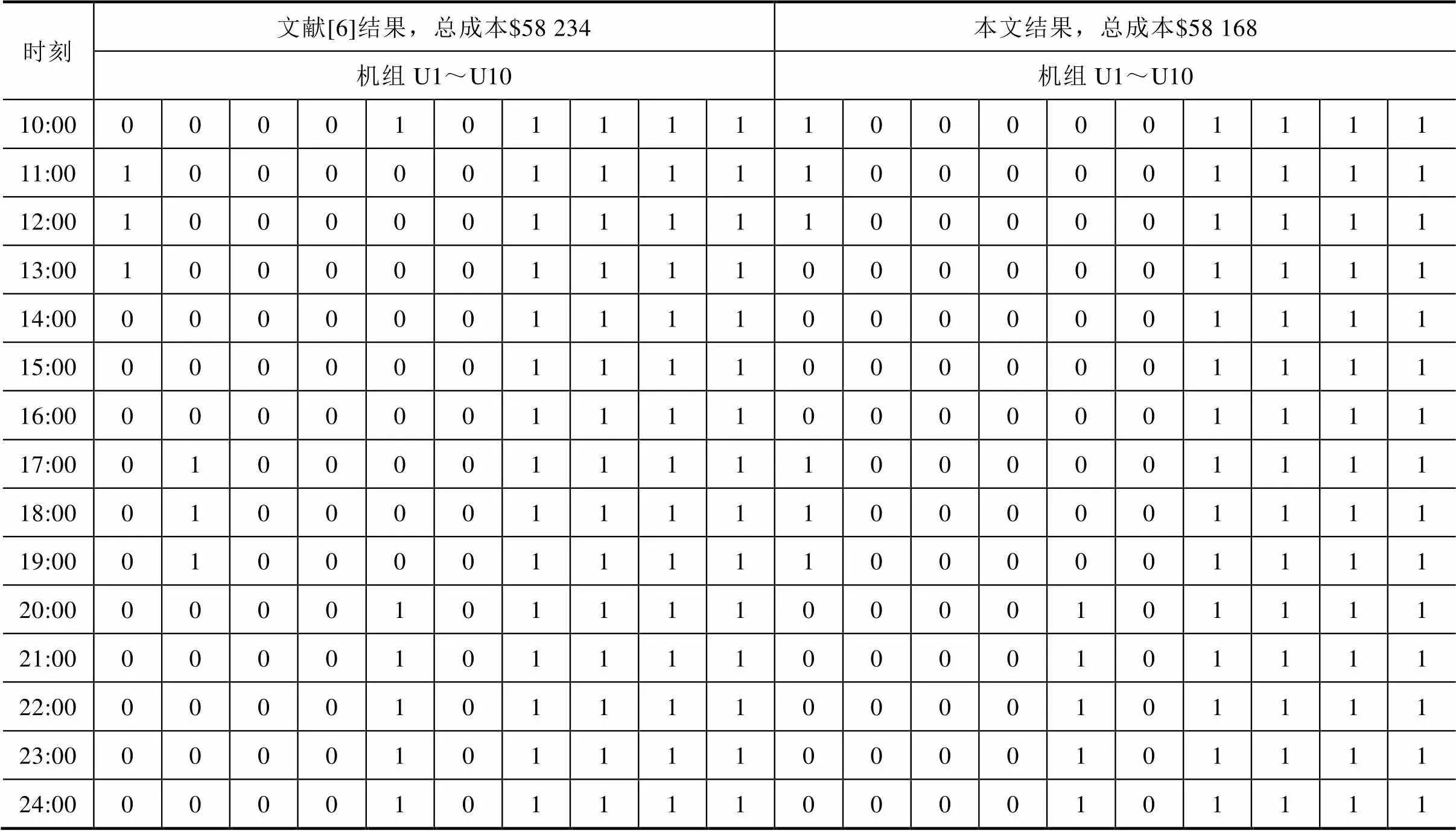
（续表3）

3.2 考虑时变备用需求机组组合滚动优化分析

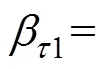
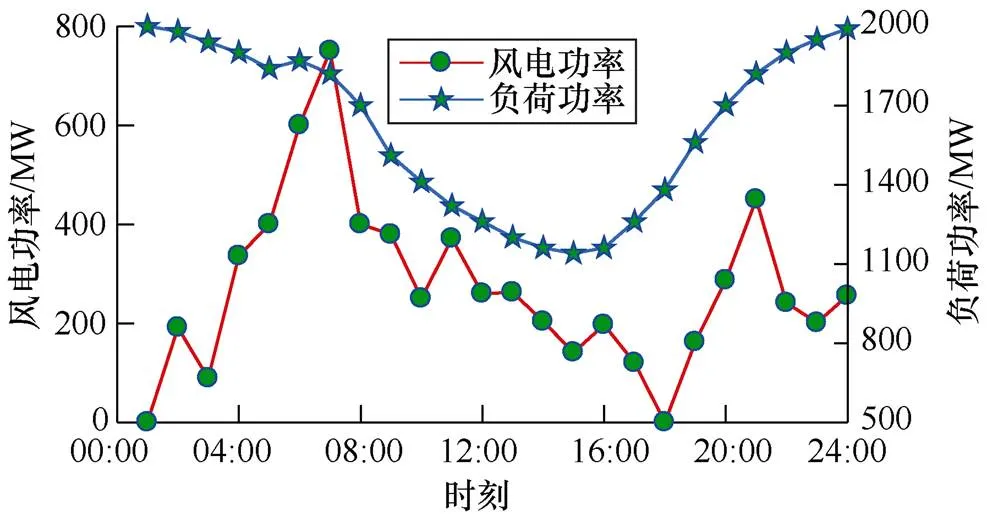
图4 负荷及风电功率预测曲线

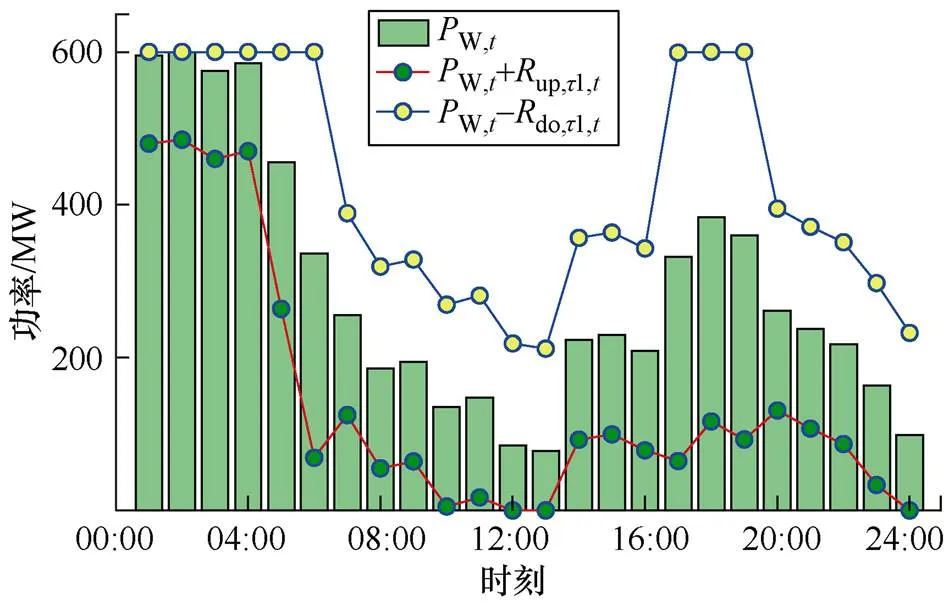
图5 第一阶段风电功率及额外旋转备用曲线

从图4和图5中曲线发现，系统需要旋转备用需求并不与风电功率正相关，1:00～4:00期间，风电预测值最高，但系统向上旋转备用需求并不最高，小于17:00～19:00期间的旋转备用需求。这是由于风电预测误差分布与风速相关，1:00～4:00期间风速较高，接近或超过风机额定风速，而此风速区间风机出力受风速变化的影响相对较小；而17:00～19:00风速区间风机出力受风速影响较大，因此系统需要预留更多的旋转备用。

第一阶段火电机组出力调度结果如图6所示。由图6发现，机组U7～U10经济性较好，承担基荷；而经济性相对较差的小容量机组，如U1～U4，只有当系统净负荷较高时，才会投运。同时，由于小容量机组运行灵活，其对系统灵活性具有一定的贡献，因此其在机组组合中也经常被调用。如：14:00～16:00，机组U1被调用，以弥补系统缺少的向上旋转备用容量。

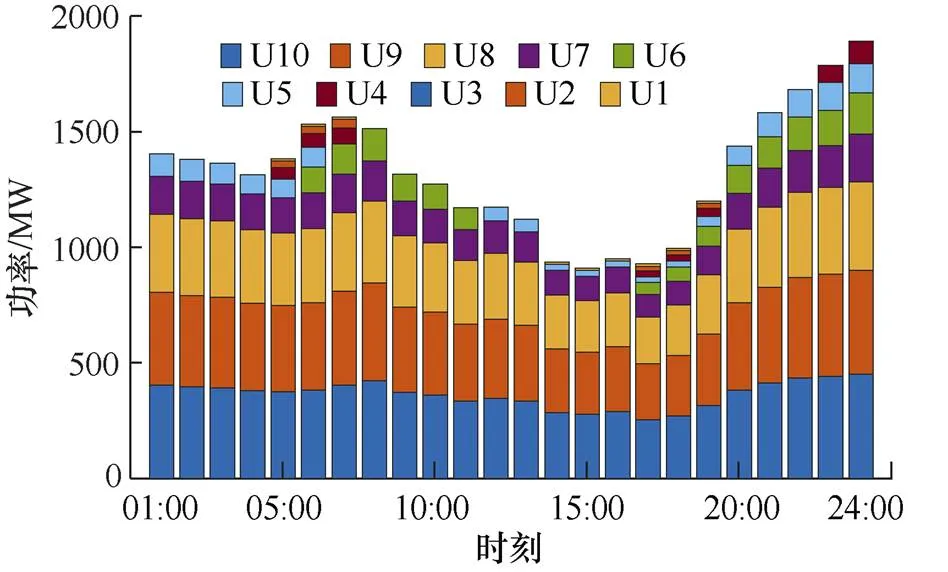
图6 第一阶段火电机组出力调度结果

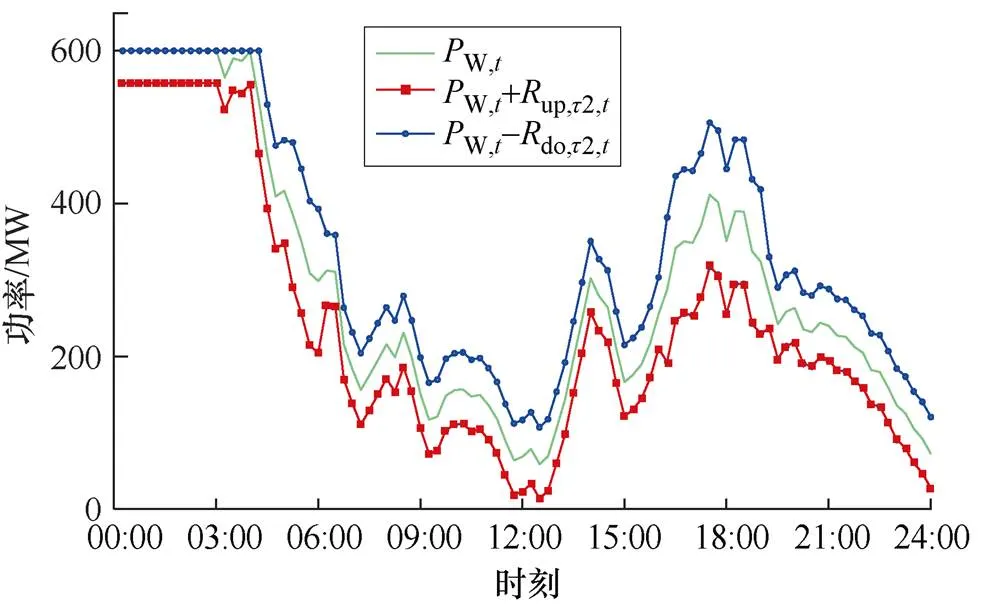
图7 第二阶段风电功率及额外旋转备用曲线

两阶段各小时燃料成本见表4。比较日前机组组合和机组出力调整两阶段各小时燃料成本发现，当风电发电量相等时，火电燃料成本并无明显差异。通过滚动优化中的超短期机组出力调整能够考虑风电功率预测误差的时变特性，充分计及风电不确定性，在不增加系统运行成本的情况下，量化系统因风电功率预测误差带来的风险。

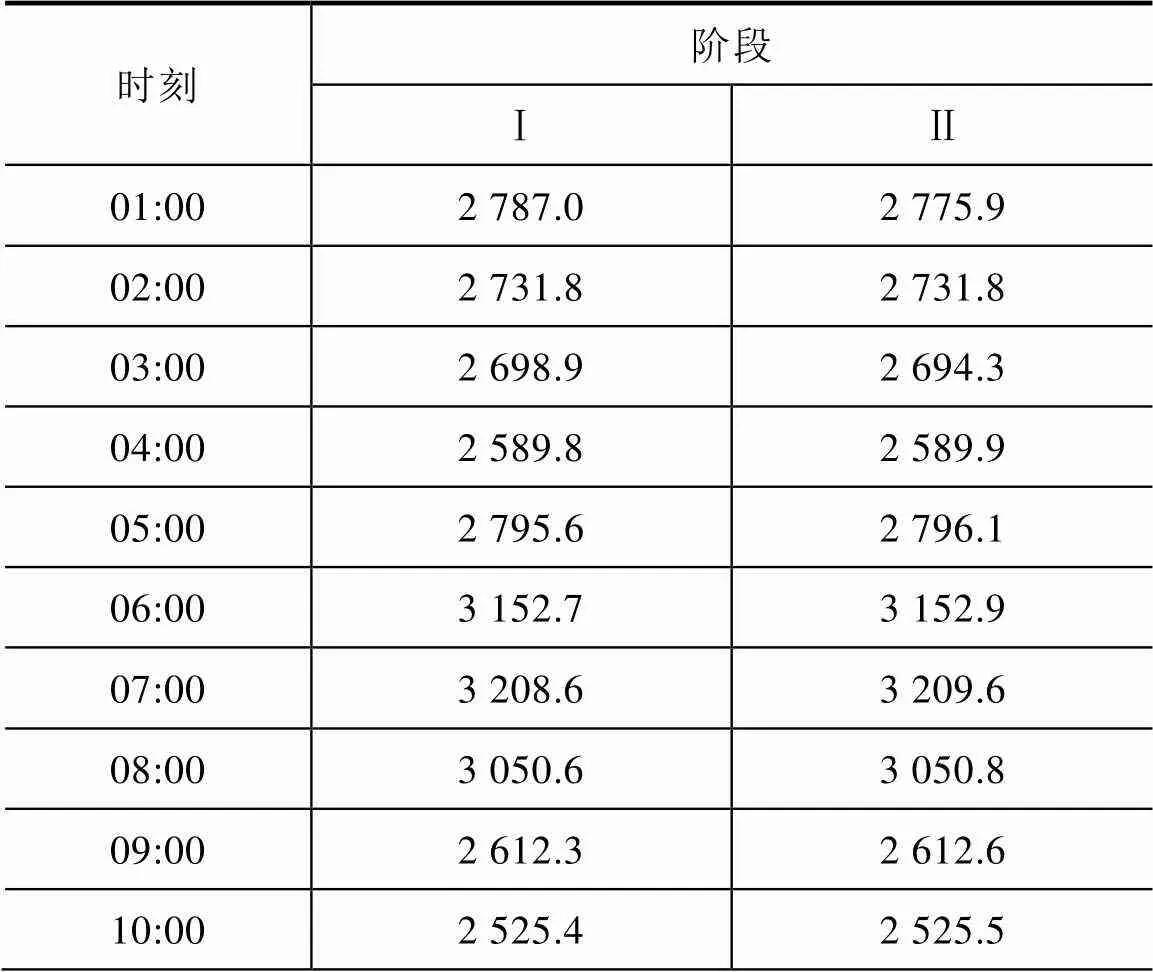
表4 两阶段各小时燃料成本 单位: $

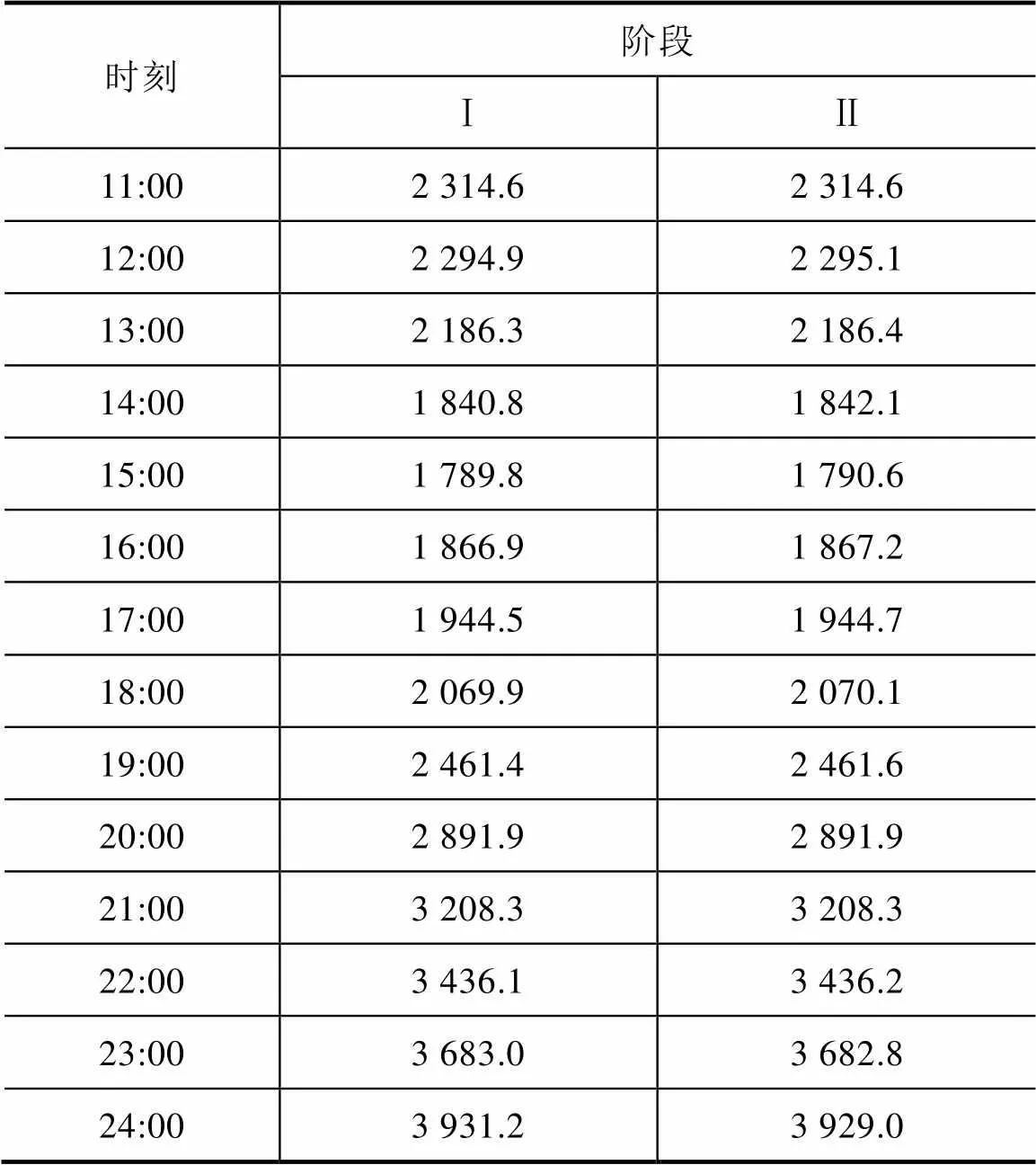
（续表4）

3.3 旋转备用概率阈值影响分析

改变第一阶段旋转备用概率阈值，保持第二阶段备用概率阈值不变，分别进行机组组合滚动优化，得到两阶段的系统总运行成本如图8所示。分析结果发现，系统总成本随备用概率阈值增加，具有明显的增长趋势，且第一、第二阶段总成本维持基本相同，这说明系统运行成本主要受第一阶段风电预测特性及旋转备用容量影响，第二阶段风电预测结果较为准确，对系统运行影响较小。

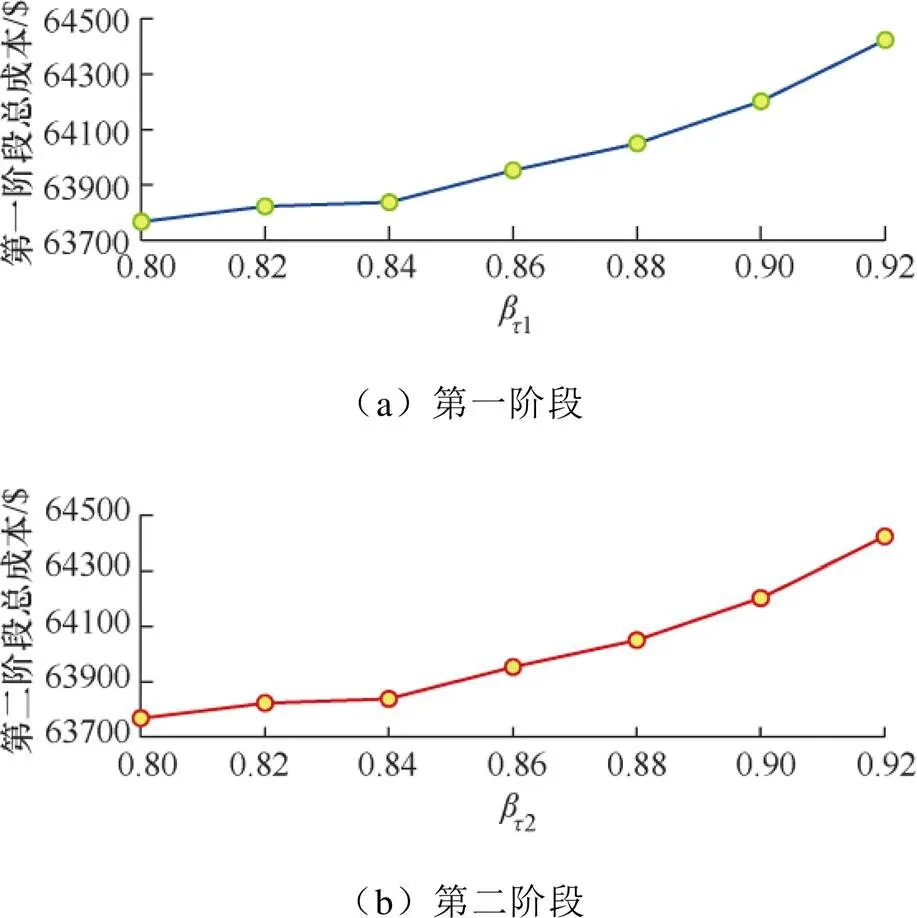
图8 两阶段系统总运行成本

4 结论

风电的间歇、波动特性给电力系统调度带来了困难，系统机组组合需预留足够的旋转备用容量以满足风电波动和预测误差。风电功率预测误差具有很强的时变特性，影响旋转备用需求。本文针对风电预测误差的时变特性，提出考虑时变备用需求的含大规模风电电力系统机组组合滚动优化模型。

算例分析表明，本文模型能充分考虑风电预测误差的时变特性，确定系统时变的旋转备用需求，滚动优化机组组合运行方案，保证系统不同时间尺度的运行安全性和经济性。

[1] 谭显东, 刘俊, 徐志成, 等. “双碳”目标下“十四五”电力供需形势[J]. 中国电力, 2021(5): 1-6.

[2] 白桦, 王正用, 李晨, 等. 面向电网侧、新能源侧及用户侧的储能容量配置方法研究[J]. 电气技术, 2021, 22(1): 8-13.

[3] VOS K D, DRIESEN J. Dynamic operating reserve strategies for wind power integration[J]. IET Renewable Power Generation, 2014, 8(6): 598-610.

[4] ZHAO Changfei, WAN Can, SONG Yonghua. Oper- ating reserve quantification using prediction intervals of wind power: an integrated probabilistic forecasting and decision methodology[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3701-2714.

[5] 王松岩, 李碧君, 于继来, 等. 风速与风电功率预测误差概率分布的时变特性分析[J]. 电网技术, 2013, 37(4): 967-973.

[6] CHEN C L. Optimal wind-thermal generating unit commitment[J]. IEEE Transactions on Energy Con- version, 2008, 23(1): 273-280.

[7] 陈庆攀, 刘洋, 许立雄, 等. 含风电的电力系统鲁棒优化调度[J]. 电测与仪表, 2020, 57(8): 78-84.

[8] 刘杰, 廖胜利, 刘本希, 等. 峰谷时段模糊识别的一库多级式梯级水电站群短期调度方法[J]. 电网技术, 2019, 43(11): 4080-4086.

[9] LI Peng, WANG Zixuan, WANG Nan, et al. Stochastic robust optimal operation of community integrated energy system based on integrated demand response[J]. International Journal of Electrical Power & Energy Systems, 2021(128): 106735.

[10] PAPPALA V S, ERLICH I, ROHRIG K, et al. A stochastic model for the optimal operation of a wind-thermal power system[J]. IEEE Transactions on Power Systems, 2009, 24(2): 940-950.

[11] CHEN Sheng, WEI Zinong, SUN Guoqiang, et al. Adaptive robust day-ahead dispatch for urban energy systems[J]. IEEE Transactions on Industrial Elec- tronics, 2019, 66(2): 1379-1390.

[12] 吴晓刚, 孙荣富, 乔颖, 等. 基于风电场功率特性的风电预测误差分布估计[J]. 电网技术, 2017, 41(6): 1801-1807.

[13] 丁华杰, 宋永华, 胡泽春, 等. 基于风电场功率特性的日前风电预测误差概率分布研究[J]. 中国电机工程学报, 2013, 33(34): 136-144.

[14] ATWA Y M, El-SAADANY E F, SALAMA M M A, et al. Optimal renewable resources mix for distribution system energy loss minimization[J]. IEEE Transactions on Power Systems, 2010, 25(1): 360-370.

[15] BILLINTON R, CHOWDHURY A A. Incorporation of wind energy conversion systems in conventional generating capacity adequacy assessment[J]. IEE Pro- ceedings C-Generation Transmission and Distribution, 1992, 139(1): 47-56.

[16] 孙书凯, 董存, 王铮, 等. 考虑不同风能特征的风电中长期电量预测方法[J]. 高电压技术, 2021(4): 1224-1232.

[17] 金国彬, 潘狄, 陈庆, 等. 考虑源荷不确定性的直流配电网模糊随机日前优化调度[J/OL]. 电工技术学报: 1-12[2021-04-15]. https://doi.org/10.19595/j.cnki. 1000-6753.tces.201295.

[18] CARRION M, ARROYO J M. A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem[J]. IEEE Transa- ctions on Power Systems, 2006, 21(3): 1371-1378.

[19] 汪洋, 钟海旺, 夏清, 等. 机组检修与运行组合的协同优化[J]. 电力系统自动化, 2014, 38(21): 26-31, 76.

[20] CHEN C L, WABG S C. Branch-and-bound scheduling for thermal generating units[J]. IEEE Transactions on Energy Conversion, 1993, 8(2): 184-189.

Unit commitment rolling optimization of power system with a large-scale wind farm considering time-varying reserve requirement

GUI Qianjin1HUANG Xiangqian1MAI Li2XU Ruixiang1

(1. Anqing Power Supply Company, State Grid Anhui Electric Power Co., Ltd, Anqing, Anhui 246003; 2. State Grid Anhui Electric Power Co., Ltd, Hefei 230022)

The fluctuation and unpredictability of wind power bring difficulties to power system security and economic dispatching. The unit combination of power system including wind power needs to arrange thermal power to reserve sufficient rotating reseve capacity to reduce the impact of wind power fluctuation and prediction error on power system. In this paper, according to the strong time-varying characteristics of wind power prediction error, a rolling optimization model of unit combination in power system with large-scale wind power considering time-varying standby demand is proposed. The model fully considers the time-varying characteristics of wind power prediction error and optimizes the rolling operation scheme of system unit combination. The example analysis proves the effectiveness and feasibility of the model. The analysis shows that the model can meet the time-varying standby demand of the system and ensure the operation safety and economy of the system at different time scales.

wind power uncertainty; time-varying characteristics; rolling optimization; linear programming

2021-04-15

2021-05-07

桂前进（1975—），男，安徽潜山人，本科，高级工程师，主要从事调度与控制相关工作。