基于短时傅里叶变换和深度学习的牵引网过电压辨识

贾君宜 吴命利 宋可荐 王 琪

基于短时傅里叶变换和深度学习的牵引网过电压辨识

贾君宜 吴命利 宋可荐 王 琪

（北京交通大学电气工程学院，北京 100044）

牵引网过电压严重影响电气化铁路正常运行，对牵引网过电压进行类型辨识有利于提高牵引供电系统的可靠性。针对牵引网过电压的非线性和不稳定性，本文利用短时傅里叶变换将过电压时域波形转化为二维的时频图；先通过局部特征提取和设置阈值，实现对铁磁谐振过电压的快速识别；再利用卷积神经网络的自学习能力挖掘时频图特征与牵引网过电压信号的深层次关系，实现对机车进出分相、断路器开闭操作过电压和高频谐振过电压的识别。实验结果表明，该方法的准确度在90%以上。

过电压；短时傅里叶变换；深度学习；时频图

0 引言

近年来，电气化铁路车网匹配失稳引起的牵引网电能质量问题较多，常伴随有各种过电压现象出现，对电气化铁路的安全运行造成了干扰。如果能第一时间对牵引网过电压进行辨识，将有利于保障牵引供电系统的安全可靠性。虽然牵引变电所、机车车辆都布置有相应的电压互感器，但尚缺乏对数据的快速采集和智能辨识技术。

目前有多种电压检测分析方法[1-10]可以应用于对牵引网过电压类型的识别，一般包含两个关键步骤：电压信号的时频域变换和时频特征的提取与识别。对于电压信号的时频域变换，比较成熟的方法有时域法[1]、快速傅里叶变换（fast Fourier transform, FFT）[2]、短时傅里叶变换（short-time Fourier transform, STFT）[3]、小波变换（wavelet transform, WT）[4-6]和S变换[7]。时域法一般将时间序列划分为多个区间，分析不同区间上信号的时域特性。快速傅里叶变换具备时间复杂度低的特点，但只适用于平稳信号分析，对暂态信号的灵活性较差，且快速傅里叶变换生成的频谱不具有时域特征，无法同时综合分析时域和频域。短时傅里叶变换、小波变换和S变换都应用了加窗分帧的思想，生成原始信号的时频能量图，这三者不同在于：相较于小波变换和S变换，短时傅里叶变换由于其窗函数固定，虽然具有“时间、频率分辨率不可兼得”的缺点，但是计算量小。短时傅里叶变换计算量小，更适于布置在牵引变电所或机车车辆的实时在线监测设备的终端嵌入式系统。本文采用短时傅里叶变换，并针对不同频率范围，通过调节窗函数在时域、频域分辨率之间作取舍，生成合适的时频能量图。

对于时频特征的提取与识别，最重要的是特征参数的选择和识别算法中阈值的设定，可以利用电路暂态分析和统计学方法来实现。文献[1-2]应用傅里叶变换提取过电压频域特征，并对时域信号进行分区间处理，基于统计分析设定时频特征参数与阈值，实现了过电压类型识别。文献[3]针对电力系统操作过电压特征提取这一问题，通过采用时域分析、加窗傅里叶变换、小波变换三种技术手段，找到用于区分不同过电压的特征，并且基于过电压暂态仿真模型，设置识别算法中的阈值。文献[4]将小波理论应用于船舶电网小电流故障接地时的选线问题，并对故障接地的暂态过程进行了深入的研究。以上基于特征的电压检测分析方法均需要人工选定特征参数和设定阈值，通常涉及复杂的电路暂态模型或统计学方法，且容易受到人的主观影响，特别是当分类任务的计算规模增大时，分类难度会大大增加。

随着计算机性能的提升，深度学习方法被大量运用于辨识任务中[11-14]。在以往的动车组跟车测试中，大量的牵引网网压数据被收集[15-19]，其中包含了丰富的牵引网过电压数据，可以作为深度学习的数据集。卷积神经网络（convolutional neural network, CNN）是深度学习的代表算法之一。CNN在二维数据的特征提取任务中表现出了极佳的性能，适用于时频能量图这种二维数据的特征识别。视觉几何组（visual geometry group, VGG）神经网络是一种具备小卷积核、小池化核、层数更深等特点的CNN，相较于其他的CNN，VGG具有高辨识率和强泛化性的优势。

本文针对牵引网过电压的辨识问题，先利用短时傅里叶变换处理牵引网过电压时域信号来得到时频能量图，再将VGG分类模型应用到牵引网过电压时频能量图的辨识中。本文的主要贡献与创新包括：

1）考虑到短时傅里叶变换计算量小、适用于在线监测设备的终端嵌入式系统，本文采用短时傅里叶变换对牵引网过电压时域信号进行时频域变换。并且本文根据牵引网过电压的特点，针对不同频率区间，调整短时傅里叶变换的相关参数，更全面地反映牵引网过电压的时频特性。

2）本文利用VGG神经网络分类模型，基于大量的牵引过电压时频能量图样本，实现了对五种常见牵引网过电压的辨识，并且该方法具备较高的准 确度。

1 短时傅里叶变换基础

1.1 基本定义

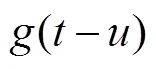
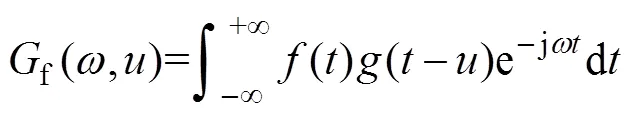
1.2 主要参数

1）时间分辨率和频率分辨率

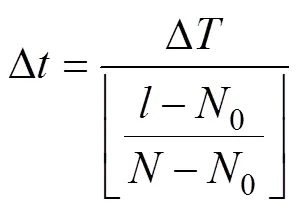
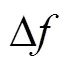
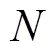
结合式（2）和式（3）可以看出，在短时傅里叶变换中，时间分辨率和频率分辨率不可兼得。

2）选择窗函数

常用的窗函数有矩形窗、高斯窗、Hamming窗和Kaiser窗。与其他类型的窗函数相比，Kaiser窗可以通过调整取值来改变窗函数主瓣宽度和旁瓣衰减的大小，实际应用范围更广，本文采用Kaiser窗，其表达式为

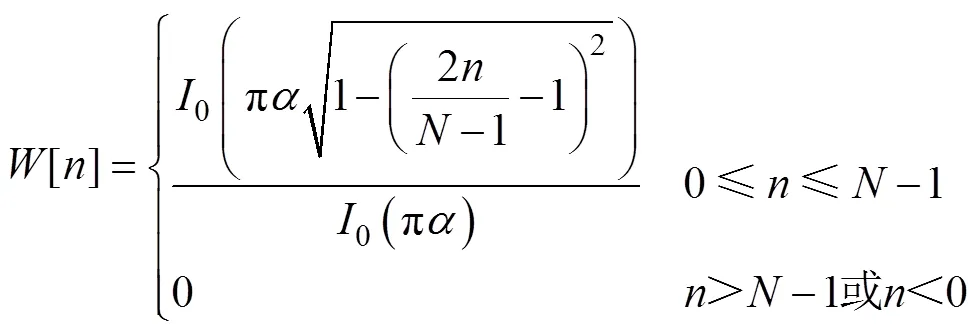
式中：N为窗函数的宽度；I0为零阶的第一类修正贝索函数；a 用来调整Kaiser窗的外形，时域上Kaiser窗的外形与a 的关系如图1所示，本文设定a =4。

3）设定窗函数宽度和重叠部分的长度

由于短时傅里叶变换存在时间、频率分辨率不可兼得的问题，又考虑到牵引网过电压类型复杂、频谱较宽，本文分情况讨论分频段（10～50Hz）和高频段（50～5 000Hz）的具体参数选择。对于分频段（10～50Hz），频率分辨率的要求较高，时间分辨率的要求较低；对于高频段（50～5 000Hz），则反之。式（5）～式（7）为限制条件，即

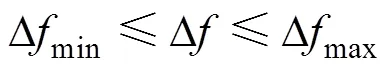
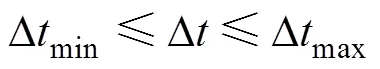
式（5）限制了频率分辨率的具体范围，式（6）限制了时间分辨率的具体范围，式（7）表明窗函数宽度小于原始数据长度，再结合式（2）与式（3），分频段（10～50Hz）和高频段（50～5 000Hz）的窗函数参数设定见表1。

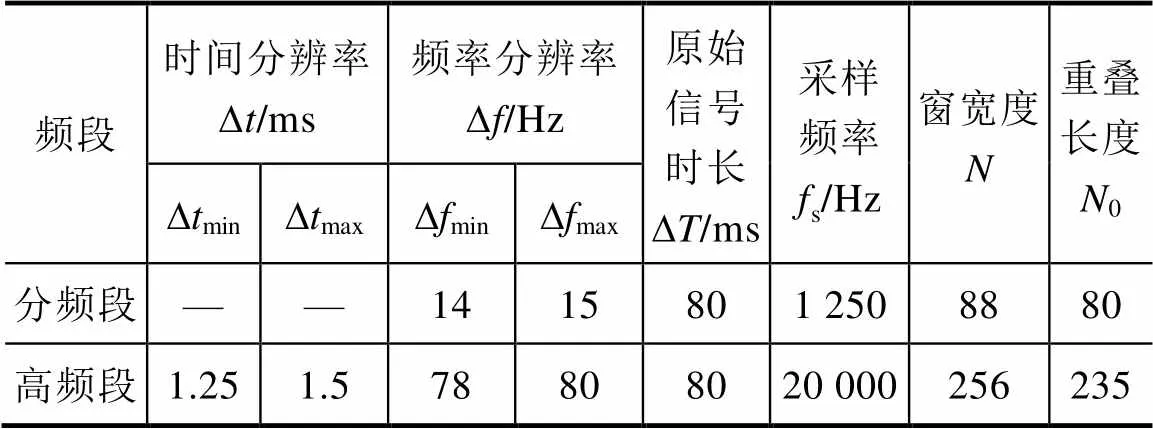
表1 窗函数参数设定

2 卷积神经网络基础

2.1 卷积神经网络的构成

一般的卷积神经网络由卷积层、池化层和全连接层构成[12]。

1）卷积层

卷积层（convolutional layer）通过在输入图像上滑动卷积核并运行一定的运算而形成特征图。这个运算具体是，卷积核的每一个元素与图像上被卷积核覆盖的区域内的对应元素分别做乘积，再将所有乘积取和。对于二维张量，卷积核的数学模型可以表示为

2）池化层

池化层（pooling layer）又称下采样层。池化是一种非线性形式的降采样方式，可以减少神经网络的参数、提高神经网络的训练速度。本文采用最大池化，其表达式为

3）全连接层

在经过几个卷积层和最大池化层之后，全连接层来实现神经网络的最终任务。全连接层的数学模型为

式中：为输出（本层）张量；为输入（前一层）张量；为权重；为偏置；为激活函数，对于识别任务的输出，为softmax函数。

2.2 卷积神经网络模型选型

常用的卷积神经网络模型有LeNet、AlexNet，VGG等。与其他几种神经网络相比，VGG具有小卷积核、多层数的特点[12]，能够取得较高的识别精度。VGG又分为VGG-16和VGG-19。VGG-16模型的结构示意图如图2所示。

图2 VGG-16模型的结构示意图

由图2可知，输入该网络的张量依次经过模块1至模块6到输出。VGG-16的结构非常简洁，通过反复堆叠3×3的小型卷积核和2×2的最大池化层，成功地构筑了16层深的卷积神经网络。

3 基于STFT+CNN的牵引网过电压辨识算法

本文提出一种基于短时傅里叶变换和VGG卷积神经网络的牵引网过电压辨识算法，该算法的核心优势在于结合了短时傅里叶变换计算速度快和VGG分类模型准确度高的优势。该算法包含四个主要步骤：波形采集、由STFT生成时频能量图、时频能量图的预处理、VGG-16分类模型的训练。

3.1 波形采集

常见的牵引网过电压类型如图3所示，常见的牵引网内部过电压包括铁磁谐振过电压、高频谐振过电压、断路器开闭过电压、进分相过电压和出分相过电压。

中国标准8编组动车组牵引传动系统由2个相互独立的牵引单元组成，牵引动力单元主要由牵引变压器、牵引变流器和牵引电机组成。跟车测试中，测试设备连接在动车组电气柜中的电压互感器低压侧。高速动车组的一个牵引单元示意图如图4所示[17]。

图3 常见的牵引网过电压类型

图4 动车组牵引单元

本文采集的过电压时序信号一共记录了4个工频周期（80ms）内的电压变化，并且采样频率为20kHz。以往的跟车测试包含上述五类牵引网过电压的数据，本文从每个类型中各抽取400个时序样本，图5为每种牵引网过电压的时域波形。

由于该样本集将运用于辨识模型，抽样必须具有代表性和普遍性。具体地：①样本集应当包含不同的过电压峰值点相位和时刻坐标，例如图5（d）和图5（e）中，过电压峰值点相位分别为90°和 313°，其时刻坐标分别为45ms和16.8ms；②样本集应当包含不同的过电压峰值，本文选取的样本集中，过电压峰值范围是45～70kV。

3.2 STFT生成时频能量图

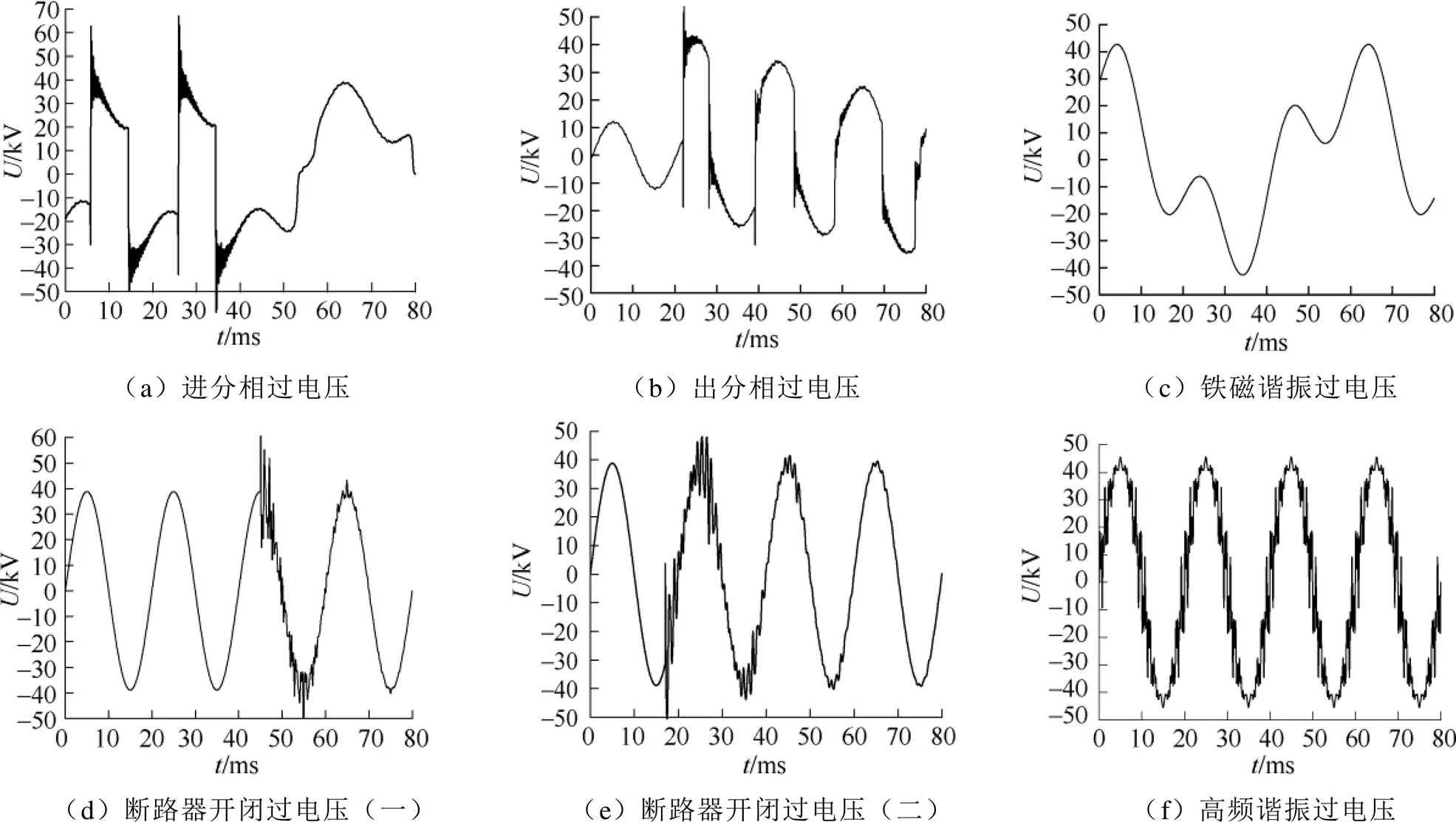
图5 牵引网过电压的时域波形

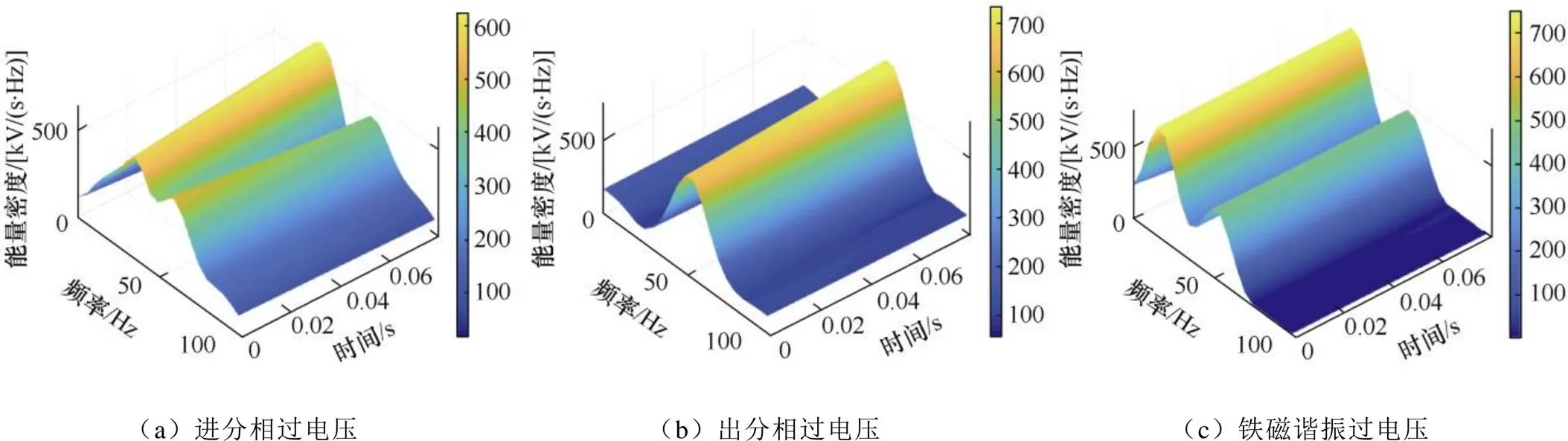
对于高频段（50～5 000Hz），保持原始信号的采样率（20 000Hz），原始信号由STFT生成时频能量图后，为更全面地观察能量密度与时间、频率的关系，选取时频能量图的频率范围区间为[0, 5 000Hz]。图6所示为几种牵引网过电压的高频段的时频能量图。

图6 牵引网过电压的高频段的时频能量图

对于分频段（10～50Hz），需要将原始信号的采样率降至1 250Hz，原始信号由STFT生成时频能量图后，为更全面地观察能量密度与时间、频率的关系，选取时频能量图的频率范围区间为[0, 100Hz]。图7所示为几种牵引网过电压的分频段的时频能量图。

需要注意的是，由式（1）可知，STFT直接生成的时频图的轴坐标是能量密度值，但是为了在三维图上更全面地展现时频图的特征，图6中的轴坐标选用能量密度的分贝值，两者之间的关系为

式中：dB为能量密度的分贝值；f为能量密度值；0为标准值，这里取1。

由图5～图7和表2可知，每种牵引网过电压均具有一定的时频特征，这证明基于时频特征的辨识方法是可行的，然而其更深层次的信息需要进一步分析，因此本文利用深度神经网络对STFT时频能量图进行数据挖掘，实现对过电压的辨识。

3.3 时频能量图的预处理

1）铁磁谐振过电压的快速识别

观察图7可知，铁磁谐振过电压和进分相过电压在分频段的时频能量图有明显特征：[0Hz, 30Hz]区间的能量密度大于[30Hz, 60Hz]区间的能量密度；再结合图6和表2，铁磁谐振过电压在[250Hz, 5 000Hz]区间的能量分贝值明显小于其他类型的过电压。此外，根据铁磁谐振过电压的暂态分析[16]，可知牵引网的铁磁谐振主要为1/3工频、1/5工频谐振，且几乎不含高频谐波分量。因此，本文采用分频段特征比较、高频段设置阈值的方法来完成对铁磁谐振过电压的快速识别，图8为分频过电压的快速识别流程。

表2 牵引网过电压的时频特征

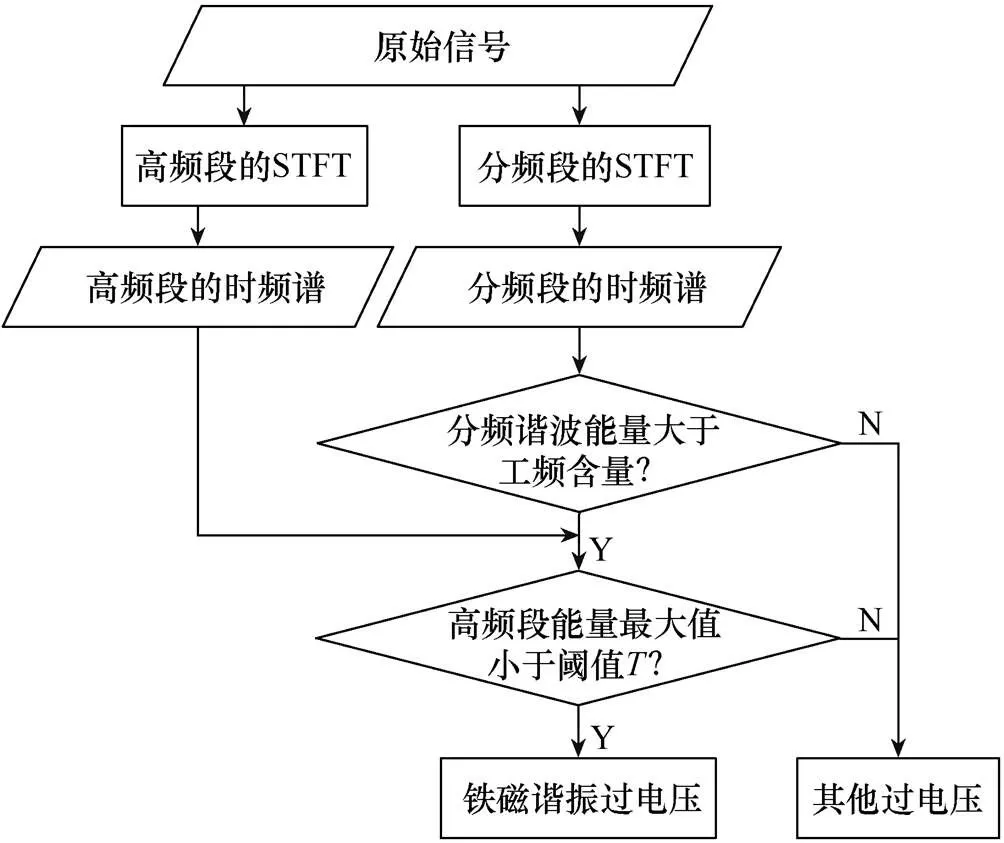
图8 分频过电压的快速识别流程

2）神经网络样本集的生成

观察图6和表2可知，对于牵引网在高频段的时频能量图，0～250Hz部分的平均能量值大于250～5 000Hz的平均能量值，原因是过电压的基波（工频50Hz）幅值一定大于谐波幅值。然而250～5 000Hz部分也包含重要的特征信息，如果直接将未经任何处理的时频能量图用于神经网络的训练，神经网络可能会忽略某些信息、造成误差。由文献[1-2, 15]可知，牵引网过电压的FFT基波（50Hz）幅值是谐波（250Hz及以上）幅值的10倍以上，因此本文将[250Hz, 5 000Hz] 区间时频图的能量密度值乘以10，生成的新的二维张量的尺寸是64×64，图9为四种过电压经过局部放大后的时频能量图，图上颜色的明暗反映了能量密度的强弱；为提高神经网络的训练速度，再将时间和频率的分辨率均降至原来的一半，最终得到32×32的二维张量并作为神经网络样本。

图9 经过局部放大后的时频能量图

3.4 VGG神经网络训练

考虑到经处理后的时频能量图的尺寸只有32× 32，所以本文将原本VGG-16的最后一个最大池化层去掉，少进行一次最大池化，最后得到2×2×512的张量传入全连接层。VGG-16神经网络训练过程中张量尺寸的变化如图10所示。

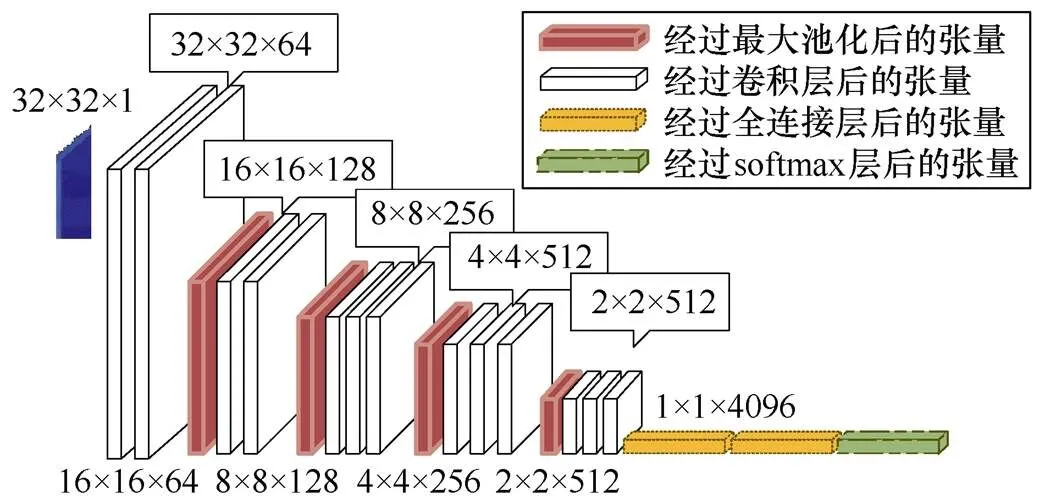
图10 VGG-16神经网络训练过程中张量尺寸的变化

样本集中每种类型的过电压均包含400个样本，共计1 600个样本。在本文的实验中，训练集、验证集和测试集的容量分别是1 120、160和320。为了使模型不断优化，选用的损失函数是交叉熵损失函数。优化器选Adam，学习率为0.005。为提高运算速度，采用分批训练，每批包含280个样本。

3.5 整体流程

综上所述，基于STFT+CNN的牵引网过电压识别的整体流程如图11所示。整体流程可分为四个主要步骤：波形采集、由STFT生成时频能量图、时频能量图的预处理、VGG-16分类模型的训练。

4 实验结果

实验平台配置的显卡是NVIDIA GeForce RTX 2080Ti，搭配酷睿i9—9900K处理器。本文先利用Matlab中的时频工具包，对动车跟车测试得到的牵引网过电压时序信号数据进行STFT，生成时频能量图并做预处理；再通过分段比较、设置阈值来快速识别铁磁谐振过电压；最后本文利用tensorflow2.0+ keras框架构建VGG-16神经网络，实现对其余四种过电压类型的辨识。

VGG-16模型训练过程中将样本分批训练以提高训练速度，每批次包含280个样本。每次迭代完成后记录并比较分析测试集和训练集上的准确度（accuracy）。

总体准确度的定义是：识别正确的样本占全部样本的比例，表达式为

式中：S为样本总数；为识别正确的样本数。

单一类准确度的定义是：某类样本中识别结果正确的样本的占比，表达式为

4.1 正则化对实验结果的影响

过拟合是指模型过度严格地依赖已有数据，而不适用于新数据。深度学习中，过拟合的具体体现是，当迭代次数超过某个值后，随着迭代次数增加，已有数据（训练集）准确度不断增大、新数据（验证集或测试集）准确度却在减小。深度学习的过拟合现象，通常是由于模型参数过多、迭代次数过高。正则化是防止过拟合的行为，可以减小测试集误差、提高模型的泛化性。

随机失活（dropout）是一种正则化技术，用以在人工神经网络中对抗过拟合。随机失活能够避免在训练数据上产生复杂的相互适应，其基本原理是丢弃部分神经元。本文对VGG-16中的第一个和第二个全连接层采用随机失活方法，得到训练集准确度与迭代次数的关系如图12所示，测试集准确度与迭代次数的关系如图13所示。

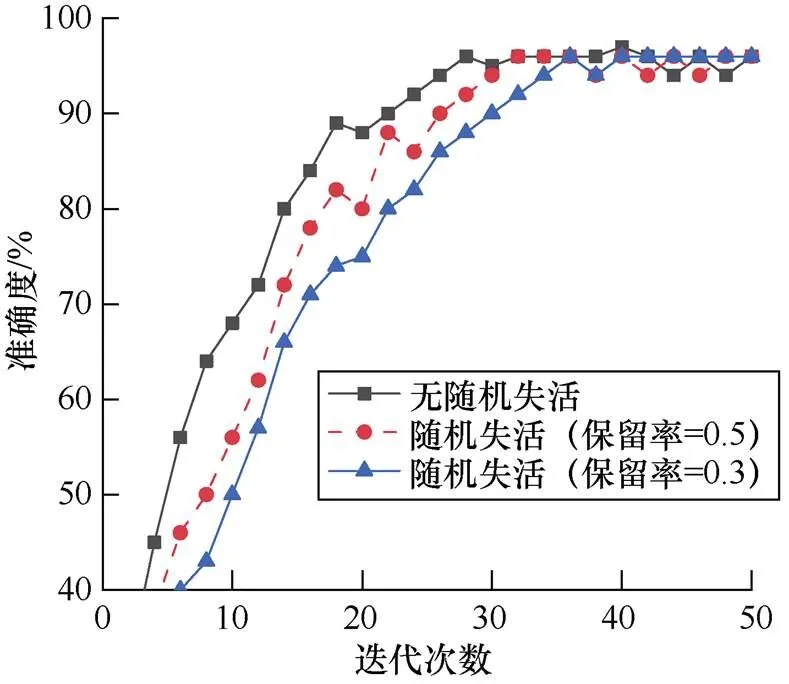
图12 训练集准确度与迭代次数的关系

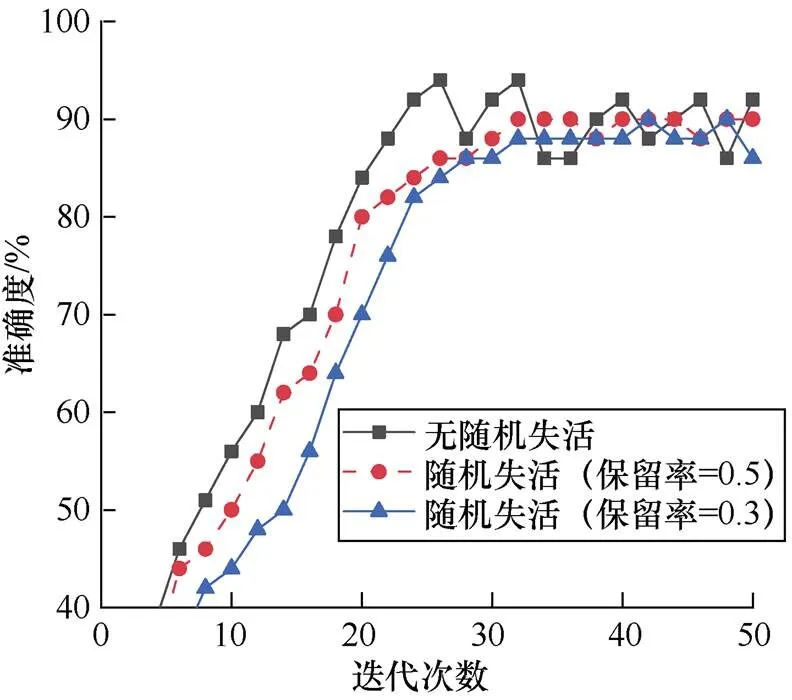
图13 测试集准确度与迭代次数的关系

由图13可知，神经网络在使用随机失活后，虽然收敛速度会降低，但是收敛后的测试集准确度较稳定，说明此时的模型能更好地适应新的样本、具有强泛化性。通过对比不同保留率下的收敛速度可以看出，随机失活的保留率为0.5适合于该分类任务。综上，本文选择随机失活，并将保留率设定为0.5，迭代30次后，分类模型的测试集准确度稳定在90%以上。

4.2 每种类型过电压的识别准确度

运用本文的方法对五种过电压进行类型辨识，混淆矩阵和每种过电压的识别准确度分别见表3和表4。表3中（1）、（2）、（3）、（4）、（5）依次代表铁磁谐振过电压、进分相过电压、出分相过电压、断路器开闭过电压和高频谐振过电压。由表4可知，本文提出的牵引网过电压辨识方法的准确率在90%以上。

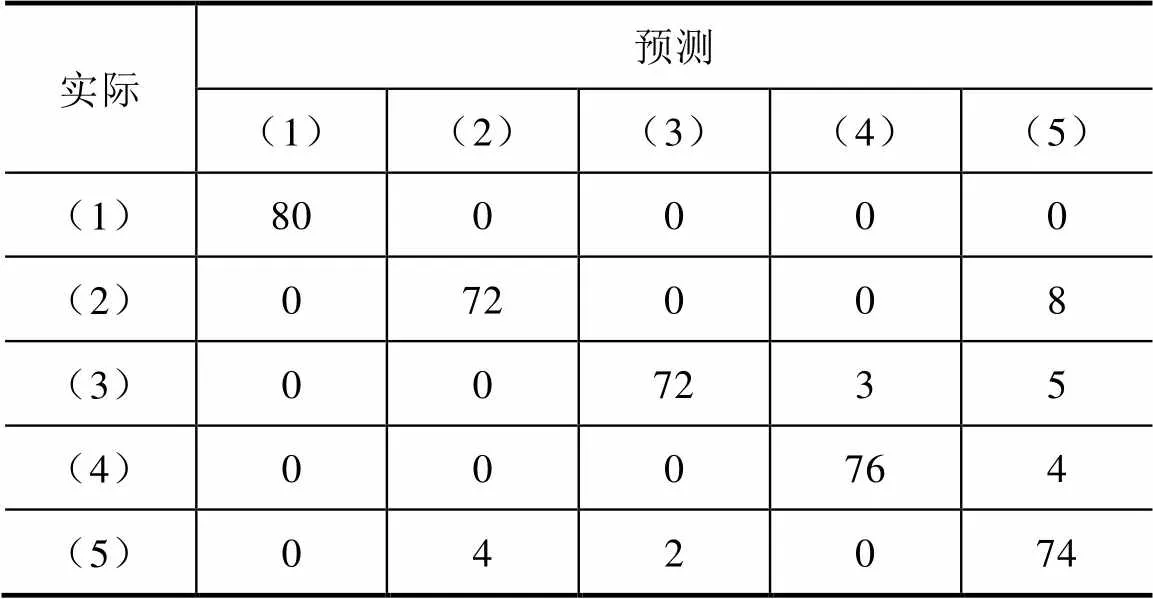
表3 混淆矩阵

表4 每种过电压的识别准确度

混淆矩阵反映了误差的来源，由表3可知，本文的辨识方法将少数进分相、出分相、断路器开闭过电压样本错误地识别为高频谐振过电压，可能是因为这些样本本身不具有明显的局部时频特征，或者含有一定的高频分量等较复杂的情形；同时，少数高频谐振过电压被错误地识别为进分相、出分相过电压，原因是这些高频谐振过电压样本含有少量畸变，导致其全局性特点减弱，属于较特殊的情形。

5 结论

本文采用短时傅里叶变换处理牵引网过电压信号，综合分析了信号的时域和频域特征，实现了对铁磁谐振过电压的快速识别；再利用卷积神经网络的自学习能力挖掘时频能量图特征与牵引网过电压信号的深层次关系，实现了对进分相过电压、出分相过电压、断路器开闭过电压和高频谐振过电压的识别。结果表明：

1）虽然短时傅里叶变换具有时间、频率分辨率不可兼得的缺点，但在实际应用中可以结合实际需要来调整相关参数，进行不同频段内的分析，在时间、频率分辨率之间做取舍。

2）训练神经网络时应当选择合适的正则化方法，如随机失活（保留率取0.5），能避免过拟合，提高VGG-16辨识模型的泛化能力，使测试集的准确度达到90%以上。

3）本文选用的VGG-16模型具有层数深、卷积核小的特点，因而收敛速度较快，通常只需要迭代20～30次即可达到较高的准确度。随着图像识别技术的发展和计算机运算性能的提高，基于时频分析的电能质量分析方法具有实际应用意义。

4）本文的辨识方法的局限性体现在两个方面：首先，神经网络的表现依赖样本集，当样本集存在缺陷或实际情况变复杂时，神经网络的性能可能下降；其次，该方法对样本集、预处理、STFT、神经网络的各项参数有一定要求，并且选定的参数组合的可迁移性还有待验证。

[1] JI Changlin, YANG Shaobing. Voltage online moni- toring and overvoltage identification based on train- mounted device[C]//2018 International Conference on Power System Technology, 2018: 3801-3808.

[2] 季昌琳. 牵引网电压质量监测系统开发及数据分析[D]. 北京: 北京交通大学, 2019.

[3] 张洛. 电力系统操作过电压特征提取和识别研究[D].成都: 西华大学, 2016.

[4] 张灵杰, 缪勇, 奚玲玲. 基于小波理论的频带自适应故障选线法及其在船舶电网中的应用[J]. 船舶工程, 2019, 41(增刊2): 91-96.

[5] 米正英, 王瑜, 王立东. 电弧信号小波去噪分析[J].电气技术, 2020, 21(3): 103-107, 116.

[6] 张杰, 李超, 李更达, 等. 基于小波分析的特高压直流输电线路单端电压暂态保护[J]. 电气应用, 2019, 38(7): 12-19.

[7] 李建闽, 林海军, 梁成斌, 等. 基于双分辨率S变换和学习向量量化神经网络的电能质量扰动检测方法[J]. 电工技术学报, 2019, 34(16): 3453-3463.

[8] 王春雷, 路小娟. 一种基于深度学习的电机轴承故障诊断方法[J]. 兰州交通大学学报, 2020, 39(2): 42-50.

[9] 刘创华, 何金, 张春晖, 等. GIS局部放电时域波形图像的模式识别方法[J]. 电力系统及其自动化学报, 2019, 31(10): 24-30.

[10] 严静, 邵振国. 电能质量谐波监测与评估综述[J]. 电气技术, 2020, 21(7): 1-7.

[11] 周林, 栗秋华, 刘华勇, 等. 用模糊神经网络模型评估电能质量[J]. 高电压技术, 2007(9): 66-69.

[12] 闫河, 罗成, 李焕. 基于步态能量图与VGG结合的步态识别方法[J]. 重庆理工大学学报(自然科学版), 2020, 34(5): 166-172.

[13] 张倩, 王建平, 李帷韬. 基于反馈机制的卷积神经网络绝缘子状态检测方法[J]. 电工技术学报, 2019, 34(16): 3311-3321.

[14] 杨晓楠, 孙博, 郎燕生. 基于深度学习的特高压直流闭锁故障智能调度决策[J]. 中国电力, 2020, 53(6): 8-17.

[15] 万玉苏. 高速动车组操作过电压特性与影响机制研究[D]. 成都: 西南交通大学, 2014.

[16] 李浩然. 电力机车过分相铁磁谐振现象研究[D]. 北京: 北京交通大学, 2015.

[17] 王娟. 高速铁路车网耦合系统网压振荡研究[D]. 北京: 北京交通大学, 2018.

[18] 陈继明, 许辰航, 李鹏, 等. 基于时频分析与分形理论的GIS局部放电模式识别特征提取方法[J]. 高电压技术, 2021, 47(1): 287-295.

[19] 邓睿, 刘碧, 宋文胜. 牵引供电网-多台机车耦合系统的低频振荡分析与抑制[J]. 电工技术学报, 2019, 34(增刊1): 327-335.

Traction network overvoltage identification based on short time Fourier transform and deep learning

JIA Junyi WU Mingli SONG Kejian WANG Qi

(School of Electrical Engineering, Beijing Jiaotong University, Beijing 100044)

Traction network overvoltage affects the normal operation of electrified railways. Identification of traction network overvoltage is helpful to improve the reliability of traction power supply system. In view of the nonlinearity and instability of traction network overvoltage, the short-time Fourier transform is used to convert the time-domain waveform of overvoltage into two-dimensional time-frequency diagram. Fast identification of ferromagnetic resonance overvoltage is realized by feature extraction and threshold setting. Then the self-learning ability of convolutional neural network is used to analyze the deep relationship between the time-frequency diagram characteristics and the overvoltage of traction network. The convolutional neural network realizes the identification of into/out neutral-section overvoltage, vacuum circuit breaker overvoltage and high-frequency resonance overvoltage. The test result shows that the accuracy of this method is over 90%.

overvoltage; short-time Fourier transform; deep learning; time-frequency diagram

2020-12-03

2021-01-17

贾君宜（1995—），男，硕士研究生，主要研究方向为牵引供电系统理论与技术。