一种基于FSS的太赫兹滤波器特性分析

张启轩，袁明辉

（上海理工大学 光电信息与计算机工程学院，上海 200093）

引 言

太赫兹波（terahertz，THz）通常是指频率为0.1～10 THz（波长30～3 000 μm）范围内的电磁波，介于微波与红外光之间。由于太赫兹波具有许多特殊的性质，如通信容量远高于微波，能够覆盖众多大分子物质（如DNA、蛋白质等）的特征谱且无电离辐射伤害等。因此太赫兹技术可广泛应用于雷达，遥感，国土安全与反恐，高速空间通信，生物医学，医疗影像，表面探伤等诸多领域[1-3]。滤波器是诸多太赫兹应用系统所必不可少的基础器件，为应对不同场景的需求，需用到中心频率可拓展的特殊滤波器。本文提出一种基于频率选择表面（frequency selective surface，FSS）的反射型偏振太赫兹滤波器。该结构在不同的旋转角度下，具有较宽的频率可拓展范围，因此同一单元结构形状只需要设计不同旋转角度即可满足不同场景的需要，无需重新设计新型结构；同时该结构还具有高反射率低透过率的特性。

1 FSS滤波器结构及调谐原理

频率选择表面（FSS）是指一种周期性的阵列结构，在磁场中自身并不会吸收能量，通过结构的特殊性，表现出对某一频带内的频率透过性，频带外频率的反射性[4-6]，如图1所示。基于FSS的反射型滤波器[7]具有结构简单，中心反射率高，品质因数高等优点。同时，由于该结构在不同方向具有不同的等效电容和电感值，可以设计成偏振频率可拓展的太赫兹滤波器。

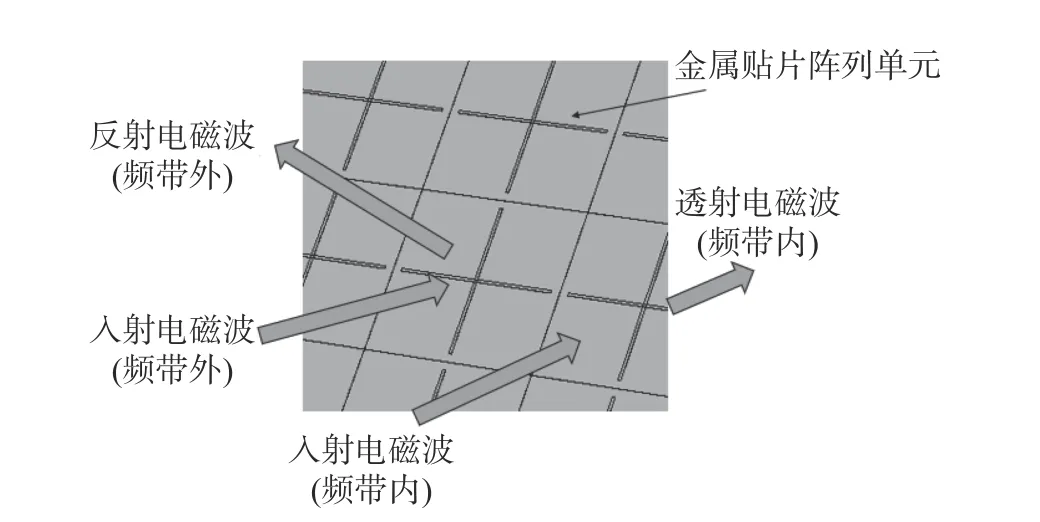
图1 频率选择表面（FSS）Fig.1 Frequency selective surface

但是，FSS的频率响应特性会受到单元结构排列方式的影响，过于紧凑的单元结构彼此之间会产生强耦合和导致栅瓣[8]的出现，如图2所示。栅瓣的产生会造成入射波能量的损耗，削弱透射波、反射波的能量，影响滤波效果。目前控制栅瓣出现的方法有：消除栅瓣或推迟栅瓣的出现[9-11]。

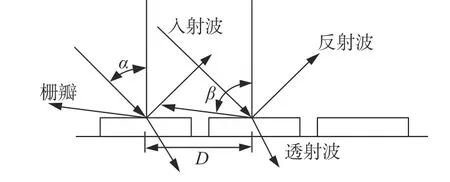
图2 栅瓣示意图Fig.2 Schematic diagram of grating lobe

栅瓣出现的条件为

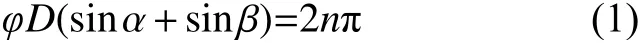
式中：φ=2π/λg，λg为出现栅瓣时入射波波长；D为阵列单元间距；α为入射角；β是栅瓣与法线的夹角；n=1,2,3······相邻单元的相位差为2π的整数倍n。

故栅瓣出现的频率fg为

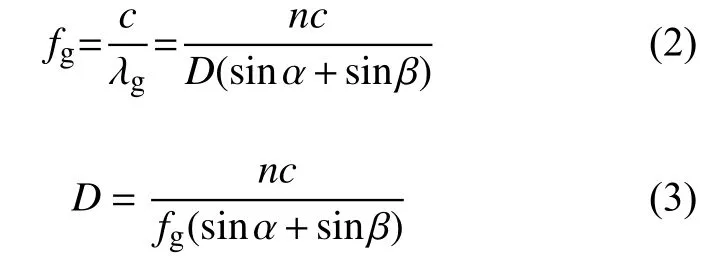
式中c为真空光速。式（2）左右移项变换得到式（3）。n=1时相邻单元相位差最小相差2π，就会出现栅瓣，当β为π/2时，栅瓣沿着阵列平面传播，此时栅瓣出现的最小频率 fg0为

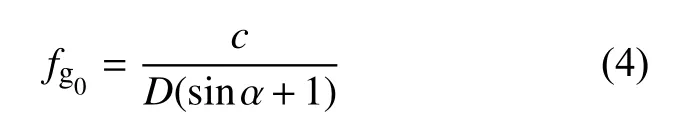
栅瓣不出现的条件是：

因此联立式（4）、（5）得到

式中λ0为入射波的波长。

当α=0°时：

经过以上公式推导，当单元结构的中心间距小于入射波的波长λ0时，可以避免栅瓣的出现。

本文提出一种基于FSS的反射型偏振滤波器，其结构如图3所示。以电磁波为作用对象，金属贴片在等效电路中等效为电感，贴片间的间隙等效为电容，因此通过调整等效电路中的电感，电容阻抗可以实现中心频率的可拓展性。

图3 金属贴片式滤波器Fig.3 Metal chip filter

缩小频率选择表面结构尺寸，提高金属贴片阵列密度来增大等效电感L和等效电容C的有效值，可使二维周期阵列结构在某些频段内对入射波表现为几乎全反射或全透射，并且FSS的频率响应特性会受到单元结构的形状、尺寸、结构间距、偏振角度、材料等因素的影响[12-13]。基于频率选择表面这种特性，设计可旋转的十字型单元结构如图4（a）所示，结构形式分别为两单臂结构整体自旋转如图4（b）所示，两单臂结构交错旋转如图4（c）所示。

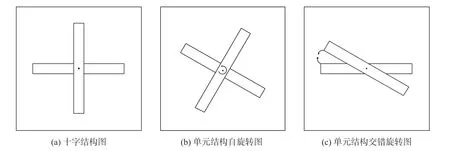
图4 单元结构图Fig.4 Unit structure diagram

实验室的测量系统最佳灵敏区间为0.6～0.7 THz左右，故仿真设计之初将阵列谐振频率设定在0.65 THz（λ约为0.46 mm）左右。为了使结构发生谐振，同时避免栅瓣的出现，依托FSS理论，当入射电场平行于二维阵列结构时，将单元中心两侧单臂长设置约为λ/2（约230 μm）。由于单元阵列间距D直接影响每个金属单元间的距离，可等效为调整单元结构的单臂长P，综上所述，单臂长P=110 μm，两臂长为220 μm，故介质基板设置为L=240 μm，d=3.6 μm，如图5（a）俯视图所示；理想的FSS阵列是无限薄的金属贴片[14-15]，一般用λ/1 000的金属贴片作为FSS屏，视为理想导体，因此，H=0.5 μm，h=0.5 μm，如图5（b）侧视图所示。金属贴片为铝，电导率为3.56×107s/m，基底为相对介电常数ε为11.9的硅。

图5 单元结构尺寸图Fig.5 Unit structure

对十字型结构进行电场分析，验证结构的可行性，如图6所示，电场分布是在中心频率0.65 THz处仿真得出的。由电场能量分布图可以看出，电场能量主要集中在金属贴片上，而且分别集中在金属贴片的各个端点，随着距离单元结构中心越远，电场能量越强，金属贴片主要发挥了电感作用；从图中还可以看出，相邻的阵列单元结构之间存在着较强的电场能量，彼此之间的间隙形成了等效电容，因此该结构具有可行性。

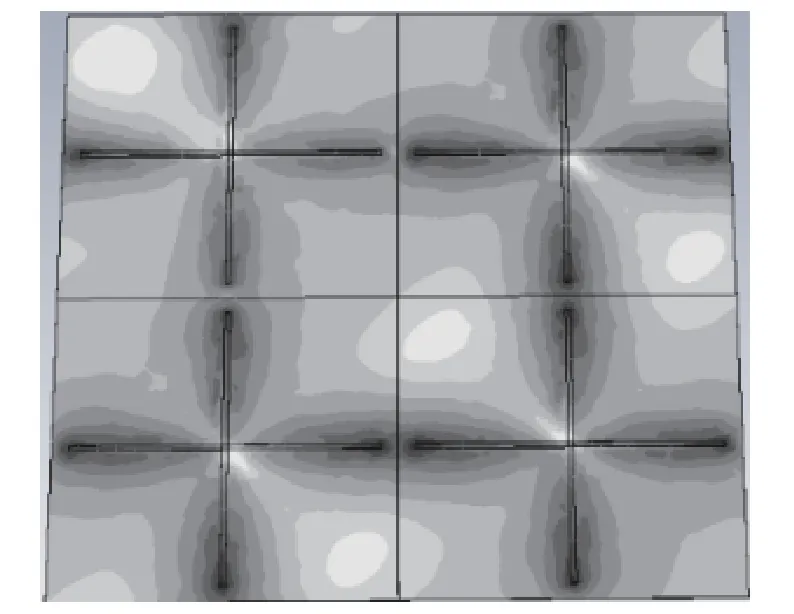
图6 电场分布图Fig.6 Electric field distribution

2 仿真计算结果

本文设计的二维阵列结构均在TM模式[16-19]下仿真完成（即电场方向平行结构，沿X轴方向），在CST（computer simulation technology）仿真中，将边界条件设置为单元阵列（unit cell），可使得周期阵列结构简化为单元结构分析，从而实现对整体周期阵列结构的空间滤波特性分析。

2.1 结构自旋转

金属贴片以单元中心为轴心，旋转一定角度θ。如图7（a）、（b）所示，旋转角度范围设定在0～45°。

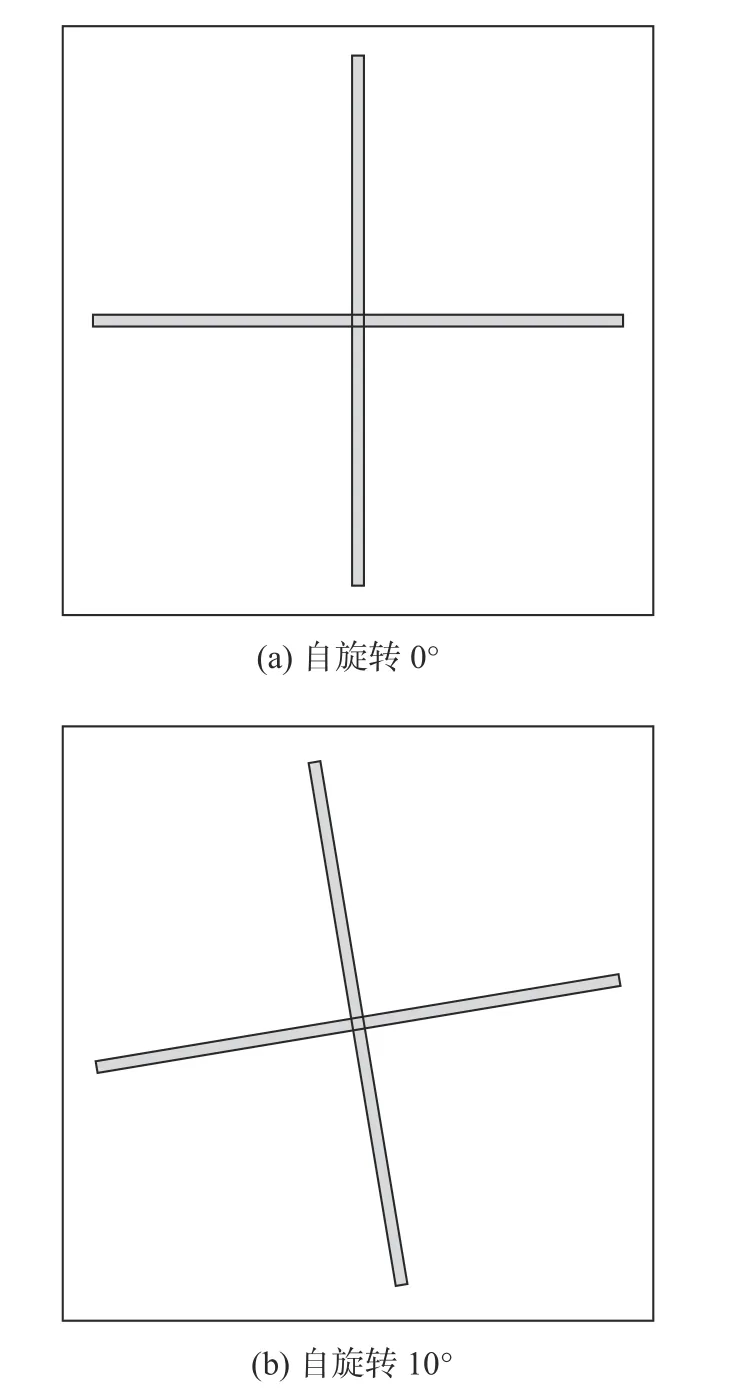
图7 结构自旋转变化图Fig.7 Structural spin change

对该阵列结构进行等效电路分析，将整体结构等效为电感，电容传输线的电路网络，所以可等效为L-C振荡电路，如图8所示。此外，不同的单元阵列结构分布，对应等效电路也是不同的，但金属贴片都可等效为电感，金属贴片间隙等效为电容，而金属尺寸、间隙距离、介质等因素又会影响电感L和电容C的有效阻抗。

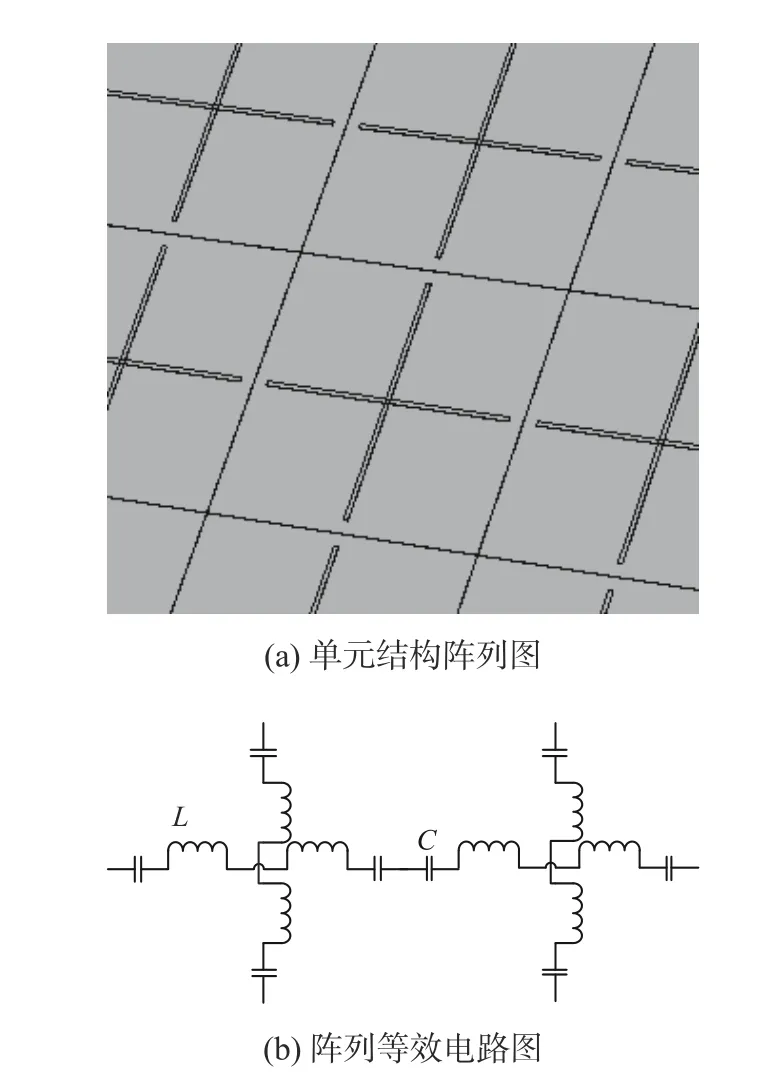
图8 贴片型频率选择表面的等效电路Fig.8 The equivalent circuit of the chip frequency selection surface

设计好的模型，根据传输线理论，其等效电感和电容为

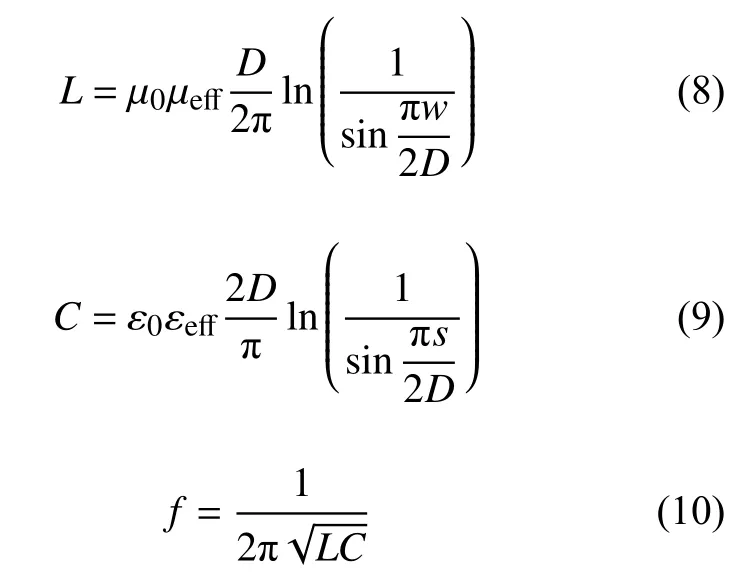
式中：D为单元阵列间距；w为金属线的线宽（结构尺寸图5（a）中的d）；ε0为真空中的介电常数；εeff为有效介电常数；s为单元之间金属贴片的缝隙，如图9（a）所示。通过对式（8）、（9）、（10）定性分析，当周期D一定时，随着旋转角度增大，缝隙s变为s1，金属贴片缝隙增大，如图9（b）所示；金属贴片线宽w，等效电容L均不变，等效电容C减小，中心频率增大，满足谐振频率与电容电感的等式关系，为接下来十字型滤波器特性分析奠定了理论基础。

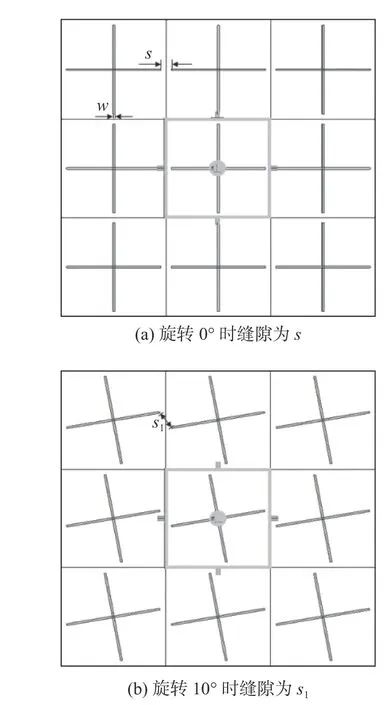
图9 单元结构自旋转图Fig.9 Spinning diagram of unit structure

从电场能量分布方面分析，在旋转角度为0°时，电场能量分布如图10（a）所示，此时对应的中心响应频率为0.65 THz；当旋转角度变为24°时，电场能量分布如图10（b）所示，此时对应的中心响应频率为0.70 THz。随着单元结构的自旋转，金属贴片的间隙逐渐增大，间隙间的电场能量也随之减弱，等效电容的容抗改变；但是金属贴片上的电场场强几乎没有变化，即等效电感没有变化，符合以上的公式推导理论。

图10 旋转前后结构电场分布图Fig.10 The electric field distribution diagram of the structure before and after rotation

通过扫频得到阵列结构的透射率曲线图如图11所示，中心频率响应变化曲线如图12所示。扫描角度从0°到36°，步进为4°；旋转结构，中心频率响应从低频向高频方向移动呈现很好的线性度，逐渐增加；低透过率，带宽变化率小，极化稳定性好，中心频率能够在0.65～0.72 THz范围内拓展，从而利用该结构不同旋转角度具有不同的谐振频率的优点适用于不同的使用场景。

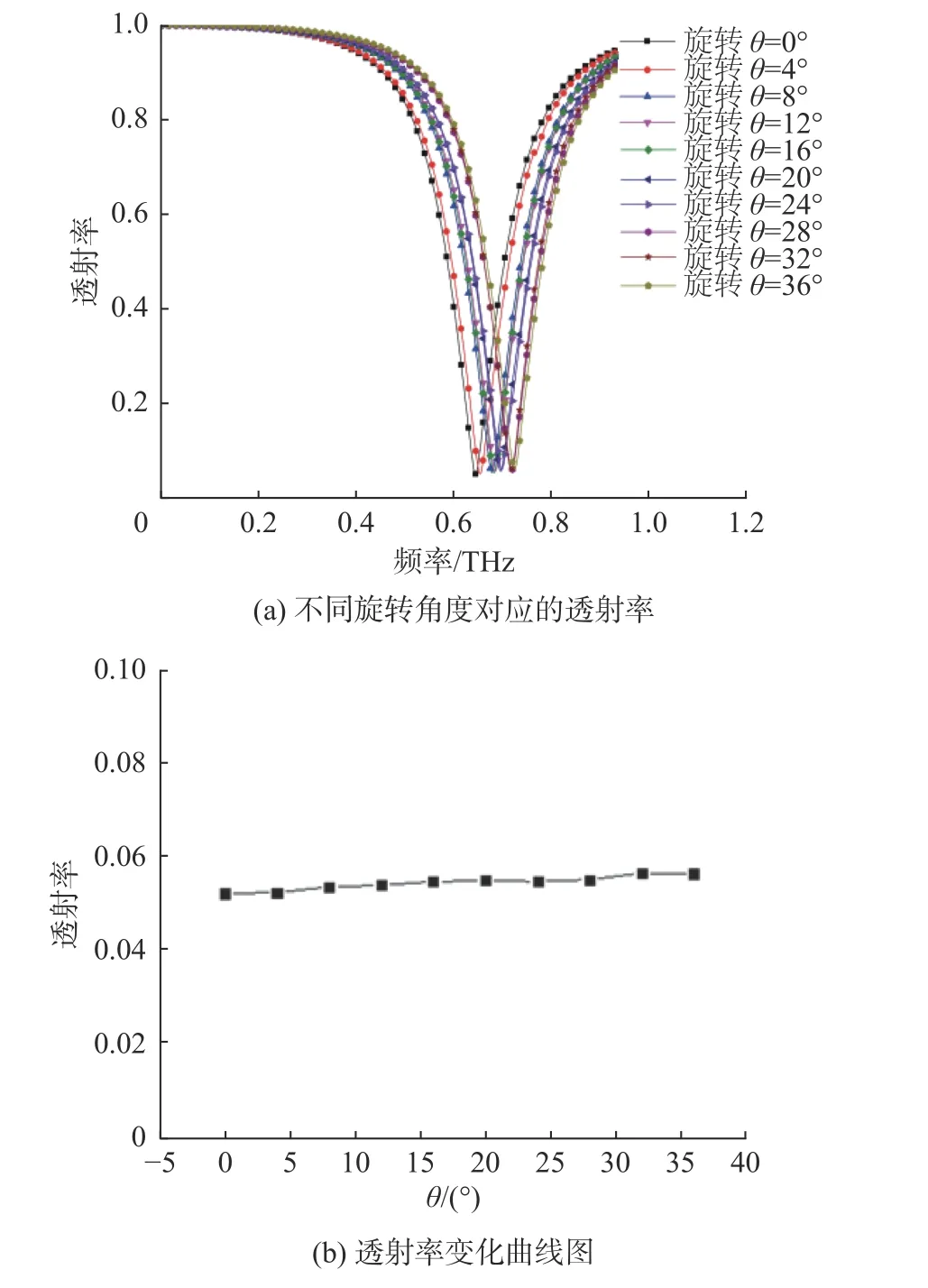
图11 旋转仿真结果图Fig.11 Rotation simulation results

图12 中心频率响应变化曲线图Fig.12 Center frequency response curve

2.2 结构交错旋转

单元结构上的金属贴片以轴心为原点，两条金属线（即十字结构的两臂）分别做反向旋转，其夹角为α，如图13所示。当电磁波垂直入射二维阵列结构时，两个金属线分别对向旋转θ，则α=π/2−2∙θ。

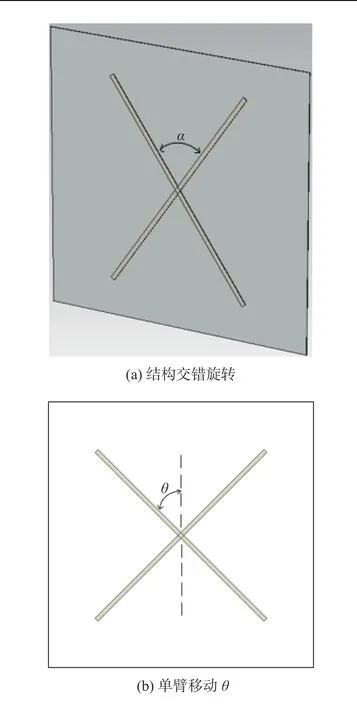
图13 结构交错旋转示意图Fig.13 Schematic diagram of structure staggered rotation

对结构做电场能量分布和等效电路分析，单元结构的电场能量分布如图14（a）所示，等效电路如图14（b）所示。由图可以看出，当金属双臂交错旋转，夹角α逐渐减小，单元阵列彼此之间电场能量越来越强，电容属性会有所增强；根据式(9)，间隙s减小，最终导致等效电容增强，中心频率向低频区移动。

图14 单元结构电场图和等效电路图Fig.14 Electric field diagram and equivalent circuit diagram of unit structure

当金属线双臂分别以5°逐步对向旋转时，α将以10°的步进逐渐缩小，中心频率会向左偏移，且偏移量增大，中心频率拓展效果很明显，带宽变化小，透射率结果图如图15所示，中心频率响应变化曲线如图16所示。

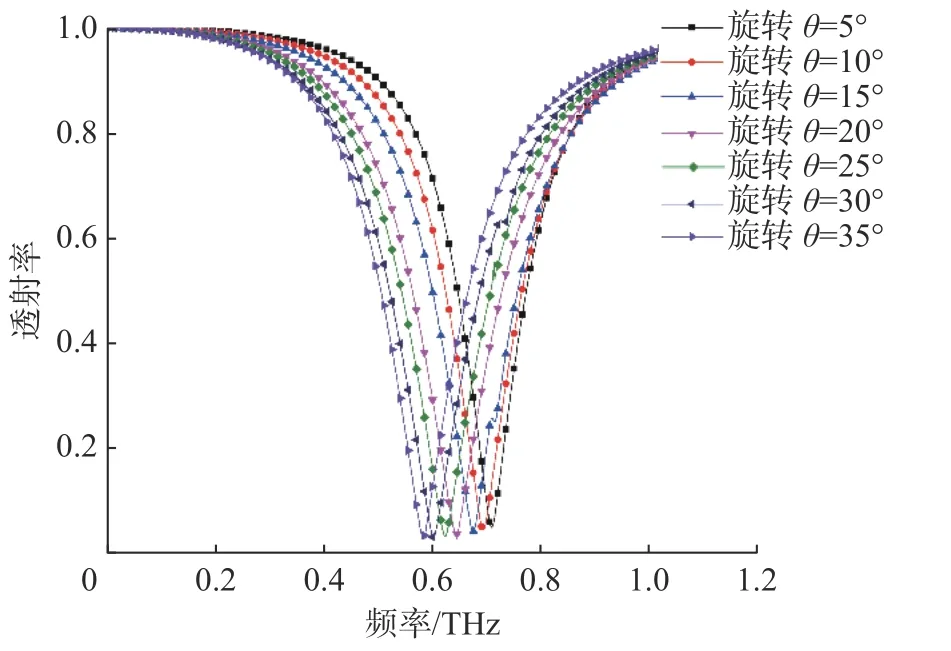
图15 仿真结果图Fig.15 Simulation results

图16 中心频率响应变化曲线图Fig.16 Center frequency response curve

当θ为35°时，金属两臂夹角α最小，二维阵列结构反射率在0.58 THz处达到96%以上，透射率低于4%，如图17所示。拓展范围将单元结构整体自旋转时的中心频率范围0.65～0.72 THz，向左拓展到0.58 THz，补充了0.58～0.65 THz这段频带的空白，使得中心频率可拓展的频带宽度达到了0.14 THz，具有较好的频率可拓展性以及稳定性。

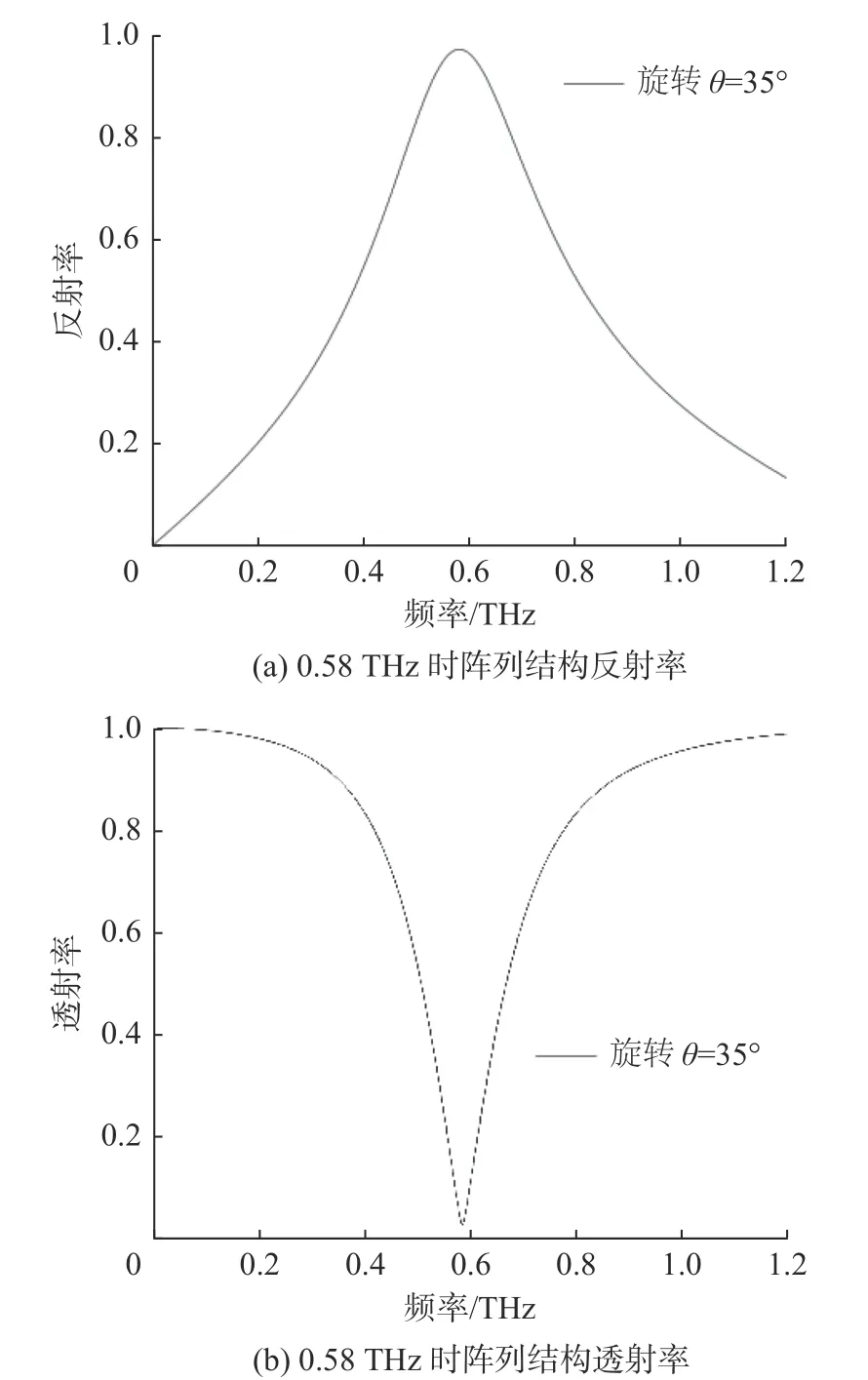
图17 中心频率0.58 THz反（透）射率Fig.17 Center frequency 0.58 THz reflection（transmission）rate

3 结 论

本文基于频率选择表面理论，设计一种十字型二维周期阵列结构的反射型偏振太赫兹滤波器，并分析了不同的旋转角度情况下，十字型结构的滤波特性和中心频率响应。通过参数优化，得出十字型结构旋转角度与谐振频率响应存在线性关系，进而使得该结构在不同的角度下，有着0.58～0.72 THz（24%）范围内可拓展性，同时其中心反射率高于96%，具有一定的应用前景。