双层硅基级联太赫兹消色差超构透镜
庞方皓,程庆庆
(上海理工大学 光电信息与计算机工程学院,上海 200093)
引 言
超构表面是一种由亚波长结构组成的超薄超材料,具备可定制的光学特性,为实现具有预期功能的平面光子器件提供了一种新颖的方法[1-2]。目前,基于超构表面设计并证实了广义Snell定律[3],并相继出现了聚焦[4-7]、偏折[8-10]、光束发生器[11-12]、光学全息成像[13-14]等。在超构表面的分支中,由亚波长结构所组成的超构透镜能够在平面内对电磁波相位进行高密度的灵活调控,区别于传统透镜通过改变电磁波光程的相位调控方式,超构透镜具备更加轻量化和更易集成化等优势。然而,受限于材料性质随波长变化的特征,超构透镜在成像中存在色差并造成图像模糊等问题,这阻碍其在光学显微成像、超分辨成像等领域的发展。
近年来,大量的研究通过对超构透镜单元结构进行优化设计并实现宽光谱的消色差成像。例如,哈佛大学Capasso团队提出了一个可见光波段的消色差超构透镜,其工作波长为490~550 nm,实现了对可见光的连续宽带消色差聚焦[15]。加州理工学院的Faraon团队设计了一个近红外波段的消色差超构透镜,其工作波长为1 450~1 590 nm,实现了近红外波段连续带宽的消色差聚焦[16]。南京大学王漱明等[17-18]设计了光频段的反射式和透射式消色差超构透镜,其工作波长为1 200~1 680 nm和400~660 nm,分别实现了近红外的消色差聚焦和可见光波段连续宽带的彩色成像。上海理工大学程庆庆等[19-20]完成了对太赫兹波段的消色差设计,分别实现了0.3~0.8 THz连续宽带的太赫兹消色差聚焦和0.4~0.8 THz连续宽带的消色差艾里光束产生。上述的消色差设计都是借助单层超构透镜结构的参数优化,使得消色差超构透镜在设计中面临数值孔径小的缺点,此外生成更好的消色差艾里光束受制于小的样品尺寸。
本文提出双层硅基级联太赫兹消色差超构透镜的方案,优化超构透镜上的结构并获得色差补偿相位为φ = 3.87π rad,从而增加太赫兹消色差透镜的尺寸和数值孔径,并且能降低高深宽比样品的加工难度。理论上将传输相位和几何相位[21]结合,分别提供频率范围从0.5 THz到1.1 THz的色差补偿相位和0.5 THz频点的聚焦相位,最终在模拟中设计并验证焦距F = 12 mm、数值孔径NA = 0.37和直径D = 9.6 mm的双层硅基级联太赫兹消色差超构透镜,其消色差聚焦示意图如图1(a)所示。本文设计的双层硅基级联太赫兹消色差超构透镜将在太赫兹探测、成像等领域发挥重要作用,有助于太赫兹消色差元器件的发展。

图 1 双层硅基级联超构透镜消色差聚焦示意图和相位分布Fig. 1 Schematic diagram of achromatic focusing and phase distribution of cascaded silicon-based achromatic metalens
1 消色差原理
设计的超构表面结构需要满足消色差聚焦透镜所需的相位分布。一束平面波经过超构透镜后聚焦,其超构透镜的聚焦相位分布如下

式中:(x, y)表示聚焦透镜平面上任意一点的坐标,透镜直径D = 9.6 mm(−D/2 ≤ x ≤ D/2,−D/2 ≤y ≤ D/2);透镜焦距F = 12 mm;c为光速;f为目标频率,取值范围为0.5(fmin)~1.1 THz(fmax),可以将式(1)的聚焦相位方程分为两部分,即聚焦相位φ1(x, y)和色差补偿相位φ2(x, y):

重点是设计一系列的单元结构使其不仅满足式(2)中描述的聚焦相位φ1(x, y),同时满足式(3)中的色差补偿相位φ2(x, y)。特别注意的是,聚焦相位φ1(x, y)仅与频率fmin相关,匹配该相位分布可以用几何相位实现,由于几何相位仅与结构单元的旋转角度有关,因此通过对特定坐标(x, y)上的结构单元引入旋转角度θ = φ1/2来满足聚焦相位分布。式(3)表示的色差补偿相位是一个与频率f成线性相关的函数,该色差补偿相位φ2(x, y)可以通过传输相位实现,通过设计不同的单元结构以此满足色差补偿相位的要求。然而,高频的相位均小于低频(图1(b)中的红色虚线位于蓝色实线下方),使得式(3)呈现一个负值的色差补偿相位φ2,这与材料的正常色散所表现出的相位随频率的增大而增大的关系相违背。因此需要给高频相位附加相移 φshift(f)=α(f−fmin) ,让高频相位大于低频相位,合并式(2)和式(3)为


2 双层硅基级联消色差超构透镜设计
双层硅基级联消色差超构透镜的设计,首要是设计并排列超构表面的单元结构以此满足色差补偿相位。我们利用有限时域差分法(FDTD)对单元结构进行仿真,设计了六种典型单元结构,柱结构和孔洞结构分别如图2(a)~(c)和图2(d)~(f)所示。单元结构的材料折射率为nsi= 3.45,x-和y-方向的周期均为px= py= 60 μm,柱(孔洞)结构的长和宽分别为L = 50 μm和W = 41 μm。图2(a)所示单层柱结构Ⅰ的衬底和柱结构高度分别为T = 150 μm和H = 250 μm,图3(a)所示为该结构的覆盖相位φⅠ= 773°和频率宽带内的转换效率均在40%以下。为了进一步增加结构的覆盖相位,将衬底和柱结构高度都增大为两倍(T = 300 μm、H = 500 μm),如图2(b)所示的结构Ⅱ。在图3(b)中可以看到结构改变后其覆盖相位增大为φⅡ= 1 554°,近似为结构Ⅰ覆盖相位φⅠ的两倍,出现部分频点的转换效率在60%(红色虚线)以上。但由于提高了单元结构的深宽比,而导致增加了样品的加工难度。为了降低结构的深宽比,我们采用双层级联的方式将两个结构Ⅰ组合形成图2(c)所示的结构Ⅲ,衬底和柱结构高度分别为T = 300 μm和H = 250 μm。如图3(c)所示该结构的覆盖相位φⅢ= 1 568°和同时大部分频点的转换效率均在60%(红色虚线)以上。对比结构Ⅰ和Ⅱ,双层级联结构Ⅲ的覆盖相位依然满足两倍关系,不仅扩大了结构的覆盖相位,同时还提升了转换效率并降低了结构的深宽比。将上述三种单元结构中的柱结构替换为孔洞结构,保持结构参数不变,形成如图2(d)~(f)所示孔洞结构Ⅳ、Ⅴ和Ⅵ。如图3(d)~(f)所示孔洞结构Ⅳ、Ⅴ和Ⅵ的覆盖相位分别为φⅣ=778°,φⅤ= 1 562°和φⅥ= 1 572°,同比柱结构的覆盖相位都得到增加。此外,转换效率在孔洞结构中同样都得到提高,其中孔洞结构Ⅵ内大部分频点的转换效率均高于60%。孔洞结构的转换效率曲线出现更多的由共振模式引起的透射峰,使得孔洞结构能够提供更大的色差补偿相位。因此我们采用双层级联的方法,结合柱结构和孔洞结构共同设计消色差超构透镜。
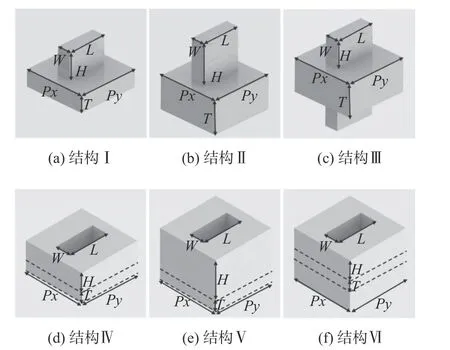
图 2 柱结构(a-c)和孔洞结构(d-f)示意图Fig. 2 Schematic diagram of column structure (a-c) and hole structure (d-f)

图 3 柱结构(a-c)和孔洞结构(d-f)的覆盖相位和转换效率Fig. 3 Phase coverage and conversion efficiency of column structure (a-c) and hole structure (d-f)
依据上述消色差理论,超构透镜通过传输相位提供工作宽带内的色差补偿相位,几何相位提供0.5 THz频点所需的聚焦相位,最终实现0.5~1.1 THz宽带消色差聚焦。将设计的所有结构参数进行整理,如表1所示,总共有34种结构,包含柱状结构(编号1~19)和孔洞结构(编号20~34)长度、宽度的结构参数和覆盖相位的数值大小。编号1~19的柱状结构提供从1 168°到1 568°的覆盖相位,编号20~34的孔洞状结构实现从1 572°到1 858°的覆盖相位。在结构排布中,孔洞结构排布在超构透镜的中心位置(−3 180 μm到3 180 μm),另外靠近透镜边缘的区域由柱结构组成(−4 800 μm到−3 180 μm和3 180 μm到4 800 μm)。由于超构透镜的对称关系,表2给出超构透镜半径上(−x方向)的单元结构排序,包含每个单元结构的坐标位置、编号和旋转角度。

表 1 单元结构参数及覆盖相位数值Tab. 1 Parameters and compensation phase of structural units

表 2 双层硅基级联消色差超构透镜单元结构排布Tab. 2 Structural unit arrangement of cascaded silicon-based achromatic metalens
3 双层级联与单层超构透镜的消色差效果
依据上述双层级联超构透镜的结构排布,利用FDTD对该超构透镜进行了消色差效果的仿真验证。如图4(a)所示为双层级联消色差超构透镜的相位曲线,其中最大色差补偿相位φ1=φmax−φmin= 3.87π rad(φshift1= φmax)。由图5(a)所示的该透镜聚焦电场强度的分布,可以看出0.5 THz和1.1 THz两个频点的焦点均在同一位置F1= 12 mm,与预期一致。两个频点的焦斑在纵向和横向上的强度归一化半高宽分别为FWHM0.5THz= 0.80 mm(横向)、FWHM1.1THz=0.35 mm(横向)和FWHM0.5THz= 3.72 mm(纵向)、FWHM1.1THz= 7.82 mm(纵向)。根据NA=n∗sinθ 计算得双层级联超构透镜的数值孔径NA1= 0.37,由 F WHM=0.5λ/NA 计算得到两个频点的焦斑横向半高宽FWHM0.5THz' = 0.81 mm(横向)和FWHM1.1THz' = 0.36 mm(横向),这与模拟仿真中测量所得的横向半高宽相接近。
双层级联超构透镜能够引入更大的色差补偿相位,是单层超构透镜色差补偿相位的两倍,以至于在相同工作频率宽带内双层级联超构透镜能够获得更小的焦距。为了更直观地说明双层级联超构透镜的特征,做了单层超构透镜的消色差聚焦效果对比。单层超构透镜由单层柱(孔洞)结构组成,结构参数与表1相同,另外旋转角度取表2中旋转角度的一半。单层超构透镜的相位曲线和仿真效果如图4(b)和图5(b)所示,其中最大色差补偿相位φ2= φmax−φmin= 1.93π rad(φshift2= φmax)为双层级联超构透镜最大色差补偿相位φ1的一半,0.5 THz和1.1 THz两个频点的焦距均在F2= 24 mm,大于双层级联超构透镜的焦距F1。此外,计算得到透镜的数值孔径为NA2= 0.19,小于双层级联超构透镜的数值孔径NA1=0.37。两个频点的焦斑在纵向和横向上的强度归一化半高宽分别为FWHM0.5THz=0.87 mm(横向)、FWHM1.1THz= 0.61 mm(横向)和FWHM0.5THz= 13.66 mm(纵向)、FWHM1.1THz=17.16 mm(纵向),均大于双层级联超构透镜的焦斑半高宽。

图 4 双层级联超构透镜和单层超构透镜的相位曲线Fig. 4 (a) Phase curves of cascaded metalens and single layer metalens

图 5 双层级联超构透镜与单层超构透镜的聚焦效果对比Fig. 5 Comparison of focusing effect between cascaded and single layer metalens
4 结论
本论文提供了一种获得大色差补偿相位的双层级联超构透镜设计方案,解决了单层超构透镜中色差补偿相位受限的问题。进一步,通过参数优化并获得0.5 THz到1.1 THz频段内的色差补偿相位φ = 3.87π rad,在仿真上设计并验证了焦距F = 12 mm、样品尺寸D = 9.6 mm和数值孔径NA = 0.37的太赫兹消色差超构透镜。本文提出的双层硅基级联太赫兹消色差超构透镜在太赫兹探测超分辨成像系统等领域具有很大的潜在应用,将会促进太赫兹成像领域的发展。

