基于微球腔的回音壁模式激光的最小尺寸研究
杨礼铨, 于佳鑫
(上海理工大学 上海市现代光学系统重点实验室,上海 200093)
引 言
近年来,回音壁模式(WGM)微球腔因具有传播模式稳定闭合、光能量密度极高、结构简单、高品质因子(Q值)、低模式体积等特点,成为微腔领域研究中的热点[1-4]。WGM微球腔是一种球形光学微腔谐振器,微腔内的光线在球形谐振腔内表面不断进行全反射,最终在腔内形成稳定闭合的传播模式,此即为WGM模式[5]。因此光场会在微腔内部,形成特定的量子化分布和极高的光能量密度。这种极高的光能量密度,能够进一步增强光与物质的相互作用,使得WGM在腔量子电动力学、量子信息处理、低阈值激光、光学传感器等方面得到广泛的应用[6-9]。
WGM微球腔制备简单,其原材料可以采用工业生产的方式得到,避免了复杂的制备工艺;同时又保留了WGM特有的光场分布,对增益材料具有特定的调节自发辐射的作用,能够对特定模式进行增强或抑制,因而在微纳激光应用方面得到了广泛关注[10]。Fu等[11]通过调节微球腔尺寸,实现室温下自由光谱范围和半高宽可调的微球腔激光;Zhao等[12]实现了在77~400 K温度范围内,通过强连续光驱动的微球腔激光。随着激光器件集成化的发展,更紧凑的微腔激光更利于激光器件的集成与应用[13]。当前,对于微球激光的研究,虽然在实验上实现了不同尺寸的WGM微球激光,但是,对于WGM微球激光的最小极限尺寸尚不清楚。
本文采用二维时域有限差分法(2D-FDTD),探究了二氧化硅微球腔放置于二氧化硅衬底上的谐振结构的光学特性。通过对不同的光学模式进行分析,得到了随WGM微球腔直径变化的不同模式特性,包含电场分布、模式有效折射率、球腔的Q值变化。同时探究了WGM微球腔能形成稳定模式、能量增益的最小球腔尺寸。这对未来WGM微球腔的进一步优化提供了理论支撑,也对微球激光的集成化应用具有指导意义。
1 物理模型的建立
目前微球腔的实际应用案例中,普遍需要与衬底或其他支持的结构相接触,可通过随机播撒或微纳操作将介质微球放置于衬底上。其中介质微球大多为工业批量合成得到,衬底一般为二氧化硅,氟化镁等常见介电材料。因而,我们采用最常用的二氧化硅介电材料,对二氧化硅微球腔放置于二氧化硅衬底上形成的结构,进行物理建模。微球腔与衬底结合的谐振结构剖面图如图1所示。其中d表示微球腔的直径大小,m表示底部二氧化硅衬底的厚度。在模拟中采用2DFDTD,使用Lumerical软件对整体的谐振结构进行理论模拟。设置底部二氧化硅厚度m =10 μm,采用材料为(n,k)的数据点集,n为材料折射率,k为材料消光系数。模拟范围内整个结构周围背景介质采用n = 1的空气,激发谐振结构的光源为偶极子光源,为了模拟无限域的同时最小化杂散光反射,使用完美匹配层作为边界条件。通过改变微球腔的直径 d 从而模拟不同大小的球腔结构。
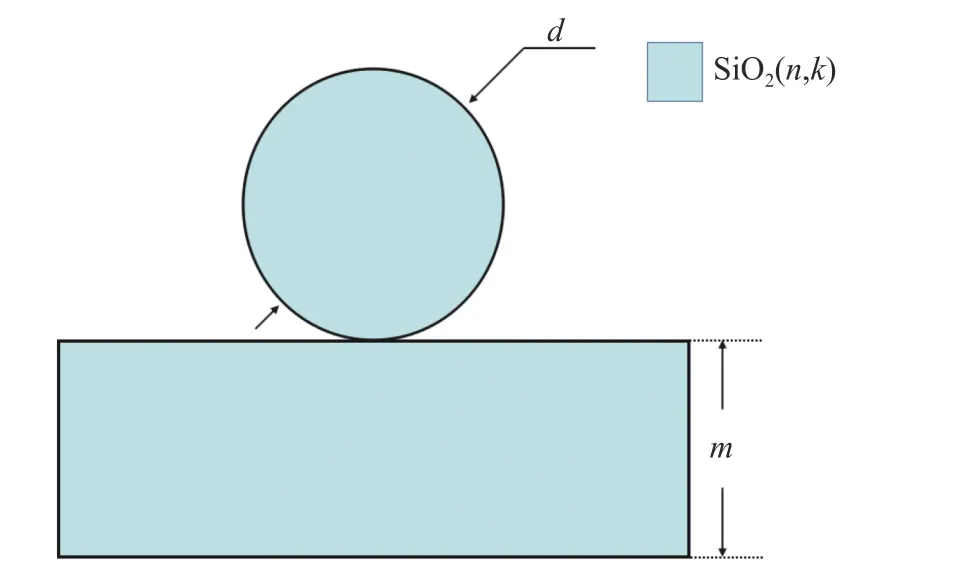
图1 物理模型剖面图Fig.1 A sectional view of the physical model
2 模拟结果及分析
2.1 不同模式的场分布特性
对不同模式电场分布的研究,得到不同的模式特征,以及二氧化硅微球腔放置于二氧化硅衬底上的模式分布。为了研究微球腔中一阶径向阶数的两种不同光学WGM模式,选取直径为8 μm的微球腔,在相同的方位角模式数情况下的电场分布,如图2所示。
根据WGM谐振峰位置处不同的模式,用红色表示TE模式,蓝色表示TM模式。图2(a)
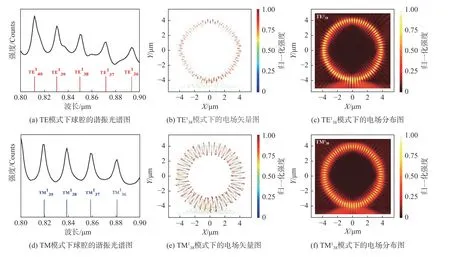
图2 直径为8 μm的微球腔两种不同光学WGMFig.2 Two different optical WGM for microspheres of diameter 8 μm

通过对上述两种基本光学模式的分析,可以发现二氧化硅微球腔中能够形成稳定均匀的WGM,但在与衬底接触的地方会产生一定的能量泄露,从而造成能量的损耗,为了得到微球激光,需要添加相应的增益介质来弥补相应的损耗,才能进一步提升在微纳激光、微纳光子器件等方面的应用。
2.2 微腔的最小尺寸分析
在实际的应用中,WGM微球腔常常与半导体材料相结合,通过在微腔内部WGM特有的量子化分布并具有极高的能量密度光场,激发半导体材料发光,将半导体材料作为增益介质,使光能在球腔内部形成更为稳定,更高能量的WGM光场分布,最终形成微球型激光。其中二维过渡金属硫族化合物材料具有体积小、发光效率高等优点,有望成为新一代高集成微纳激光的增益材料[12]。因此,以二维过渡金属硫族化合物材料为例,通过不同直径的微球腔Q值,计算出腔内能量的损耗,再与增益材料的增益相结合,当腔内增益大于损耗时,腔体内的模式更能稳定的存在,此时对应的微球腔的物理尺寸,也就是能保证模式稳定,能量增益的最小尺寸。
在WGM微腔中,腔内的能量I随时间呈指数衰减
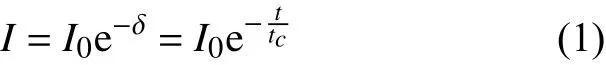
式中:I0是原始腔内能量;t是衰减时间;δ是总的往返损耗;tc是腔内光子寿命。由式(1)可得,对于腔内能量一个往返对应的衰减为

式中:Q为腔体的Q值,neff为模式有效折射率;Lc为腔内光程长度;λ为对应谐振位置的波长。得到半导体材料增益与腔损耗的关系为

式中:g为半导体材料增益。可以看出在半导体材料作为增益介质的情况下,模式有效折射率越大,增益越高。而微球腔的损耗同样与球腔的Q值和模式有效折射率有关,为此计算了不同直径下微球腔的Q值和模式有效折射率,来进一步分析微球腔增益等于损耗时的最小尺寸。
2.3 模式有效折射率
不同模式的区别也反映在模式的有效折射率上,模式有效折射率是微腔模式色散的一个固有特性,同时决定了激发不同模式所需的相位匹配条件。对于微球腔的模式有效折射率,可表示为

式中:l为方位角模式数;neff为模式有效折射率;R为微球腔半径;λ为对应的波长。对上述微球腔谐振结构的不同WGM进行计算,得到不同直径下一阶径向阶数的两种不同模式的有效模式折射率。如图3所示,计算了不同直径下在750 nm波长处的模式有效折射率。数据点表示实际计算出的模式有效折射率值,直线表示有效模式折射率的整体趋势,黑色和红色直线分别对应了光学模式TE和TM。从图3可以看出,TE模式整体位于TM模式上端,相对于TM模式,TE具有更大的模式有效折射率。
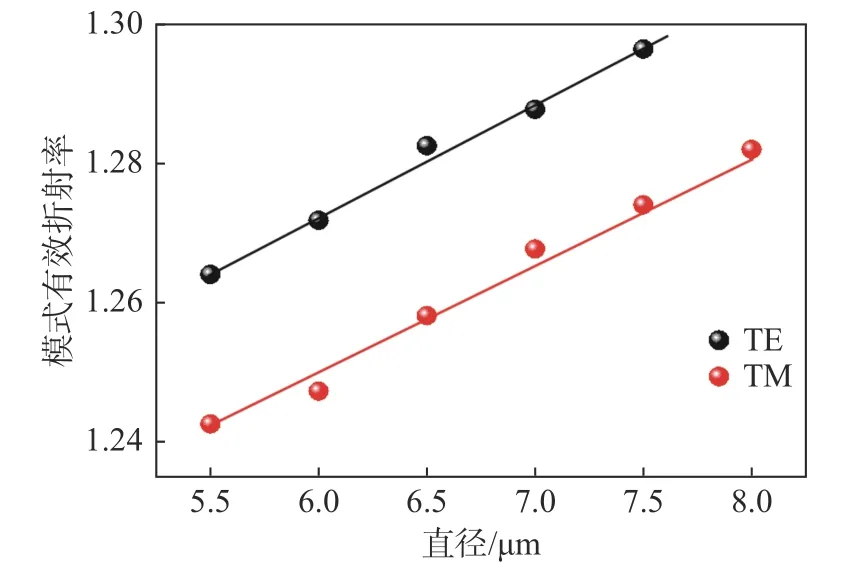
图3 模式有效折射率随微球腔直径的变化Fig.3 The mode index changes with the diameter of the microsphere cavity
通过对不同直径下微球腔的模式有效折射率计算,对基本的光学模式有了更为清晰的认识,模式有效折射率对WGM微球腔的模式光纤耦合,相位匹配都有着极为重要的作用[14]。
2.4 微球腔的Q值分析
Q值是对谐振腔光能量的存储和使光循环能力的定量描述,通常反应了微腔中存储能量以及消散能量的比值。Q值的大小也反映出微腔的质量。Q值可表示为
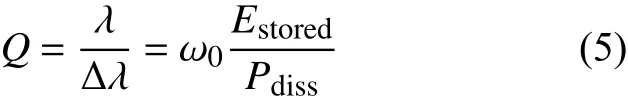
式中:λ为波长;Δλ表示波长对应峰值的半高宽;ω0为角频率;Estored为腔内储存的能量;Pdiss为腔中能量耗散的功率。利用式(5)计算了不同直径的微球腔在750 nm波长附近的一阶径向模式数下对应的Q值大小,并按照不同的模式进行了统计绘图,如图4所示。
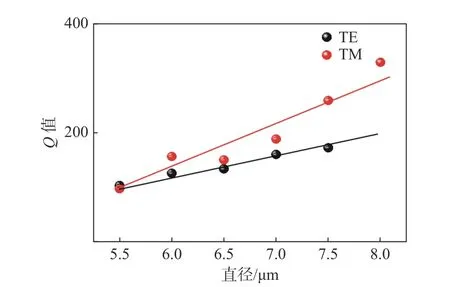
图4 不同模式Q值随微球腔直径的变化Fig.4 The value of Q in different modes varies with the diameter of microsphere cavity
从图4可以看出,Q值整体的大小随着微球腔的直径增大而增大,这也符合直径对Q值的影响特性,直径越大的微腔其Q值越大。从不同模式上看,TM模式的Q值在不同尺寸下都比TE模式的Q值要高。同时,Q值的大小也反映出腔体不同的能量损耗,Q值越大,腔内光线绕内壁一周全反射形成的WGM所损耗的能量就越小,光能在腔内保留也就越多。这在微球激光的应用领域中有着至关重要的作用。
通过上面的模式有效折射率和Q值的计算,当增益的表达式为式(3)时,此时腔内损耗等于增益,腔内模式得以稳定保留。以二维过渡金属硫族化合物(MoS2)为例,在532 nm波长连续激光激发下,其形成微球腔激光时室温下光学增益值约为2×105cm−1(实验值为1.2×105~2.3×105cm−1[12]),对于不同的模式会有较小的差异。通过分析不同直径下的电场分布,从而确定对应的增益区域大小,其中在8 μm直径附近,其模式对应的增益区域为8个方位角模式数,可计算对应的衬底接触长度约2 μm;其对应的损耗代入该模式下的Q值(280.4)与模式有效折射率(1.278),以及谐振波长748 nm进行计算。根据以上计算可以得到,当微球腔直径为7.8 μm时,微球腔的损耗与增益正好相抵消。根据尺寸与Q值的关系得出(见图4),当微球腔直径继续减小时,其Q值会减小,导致损耗增大,故而损耗会大于半导体材料的增益,所以7.8 μm是形成微球激光的最小尺寸。之前的报道中微球型激光最小在8.13 μm,也符合上述结论[11]。
3 结 论
本文通过2D-FDTD对二氧化硅微球腔放置于二氧化硅平面上的谐振结构进行模拟。通过改变不同的微球腔直径的方法,得到了形成稳定WGM的情况下,其最小微球腔激光的直径约为7.8 μm。同时分析了一阶径向模式数下的电场分布、模式有效折射率、以及球腔的Q值,为WGM微球腔的集成应用提供了理论支持。

