探测光斑尺寸对热透镜聚焦误差信号的影响

张晓荣

（山西能源学院 电力工程及自动化系，山西 榆次 030600）

引 言

热透镜技术作为光热测量技术之一，因其测量构型简单、灵敏度高等优点广泛应用于材料吸收损耗、热特性参数测量以及薄膜激光损伤监测中[1-3]。目前，热透镜技术主要采用双光束测量构型，其原理为：常规透镜在基模高斯光束辐照下，因吸收激光能量使其内部产生非均匀的温度场，从而引起折射率梯度分布，由此形成了热透镜；当另一基模高斯光束通过该热透镜后，其光强分布发生变化，通常采用前置针孔的光电探测器测量探测光束中心光强的变化。由于热透镜信号受探测光光强波动噪声的影响较大，其测量分辨率受到了限制。

2017年Domene等[4]提出了基于四象限探测器差分测量的聚焦误差热透镜技术，并将其应用于光学薄膜吸收损耗测量，获得了优于0.1×10−6的测量分辨率和极大的测量动态范围。但由于其构型参数优化条件是建立在热透镜为理想薄透镜近似理论模型的基础上，仅适用于探测光斑半径小于激励光斑半径的情形，因此无法准确分析探测光斑尺寸对聚焦误差信号的影响[5-7]。而基于热透镜光学相移理论的建模方法能够准确描述热透镜对探测光束的衍射效应，不受探测光斑尺寸大小的限制[8]。因此，本文建立基于热透镜光学相移理论的聚焦误差信号理论模型，利用该模型获得测量构型参数优化条件。通过数值计算验证构型参数优化条件的正确性并分析探测光斑尺寸对热透镜聚焦误差信号及其线性范围的影响，为进一步提高热透镜聚焦误差信号的测量灵敏度及测量准确度提供参考。

1 理论模型

图1为热透镜聚焦误差信号测量原理图，图中TL为热透镜，DT为四象限探测器，L1、L2为柱面聚焦透镜。常规透镜在激励激光辐照下因其吸收激光能量而升温，在内部形成非均匀分布的温度场，从而引起内部折射率梯度分布和表面热变形，便形成了热透镜（TL）。当激励光束为脉冲或高频方波调制基模高斯光束时，探测光同轴经过该激励激光辐照区域时，热透镜引起的探测光光学相移分布特性与激励激光光强分布特性近似相同[9]，可表示为

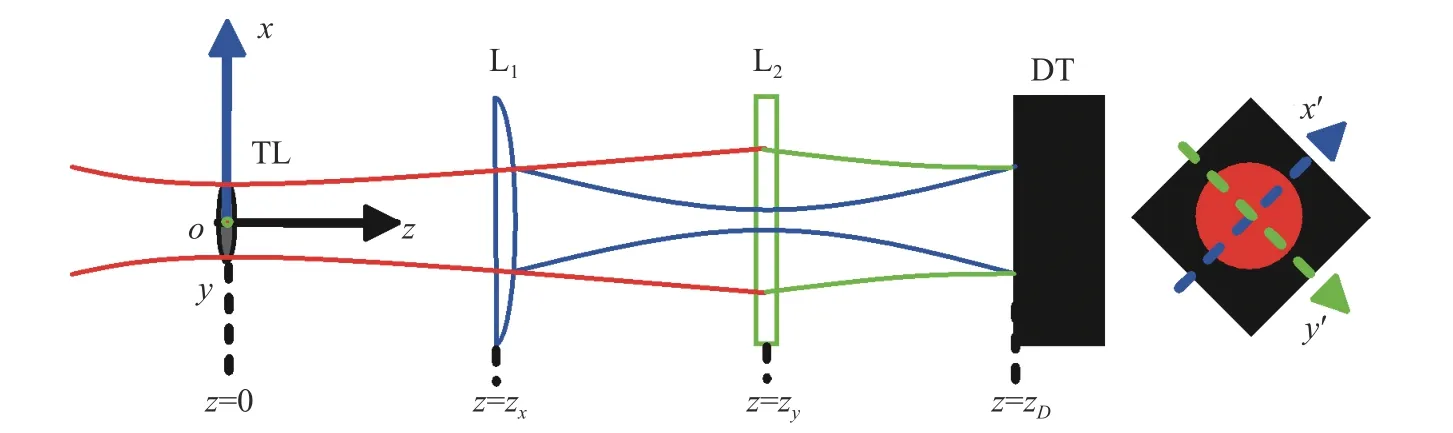
图1 热透镜聚焦误差信号测量原理图Fig.1 Schematic diagram of the defocusing measurement system

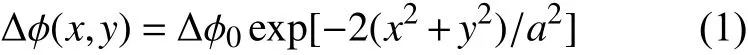
式中： ∆ ϕ0为热透镜引起的探测光束中心的最大光学相移； a 为激励光束光斑半径。

假设探测光束束腰位于热透镜位置处，经过热透镜后的探测光电场强度[9]可表示为

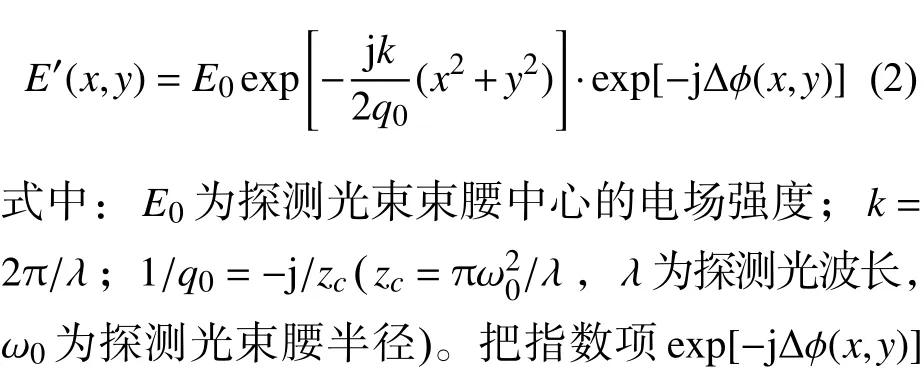
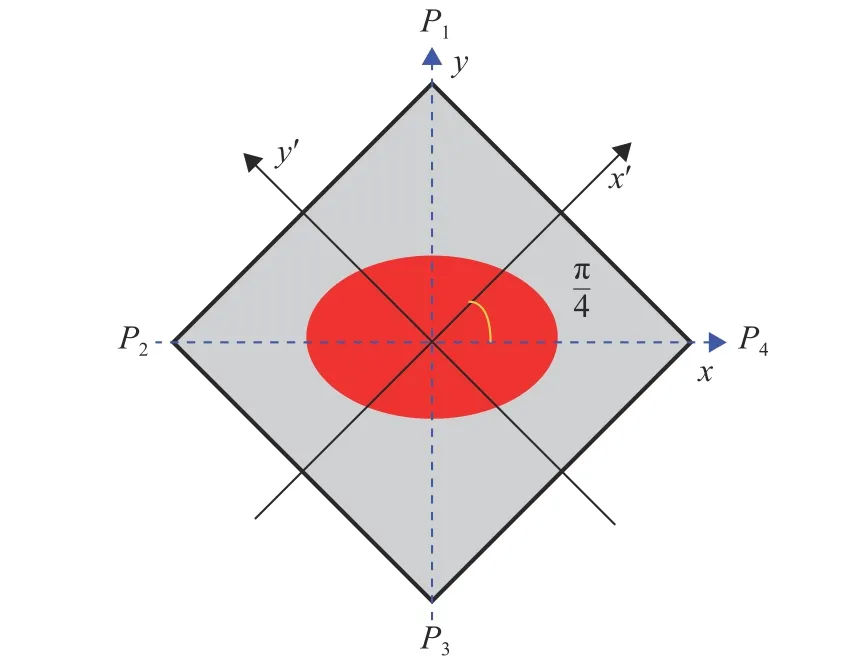
图2 四象限探测器上的探测光斑Fig.2 Probe beam on a 4-quadrant detector

从式（8）可以看出，聚焦误差信号中含有与探测光光学相移无关的信号分量，这是应为探测光经两柱面聚焦透镜变换后，在探测平面上光强呈 椭圆形分布所致。

2 构型参数优化

通常情况下，由于热透镜吸收激光能量引起的表面热变形和内部折射率变化很小，引起的探测光光学相移很小，产生的聚焦误差信号幅值较小，需要优化测量构型参数以获得最大测量灵敏度和测量分辨率。利用多元函数求极值方法得到式（8）构型参数优化条件为

对于满足构型优化条件的热透镜，其聚焦误差信号小于传统热透镜聚焦误差信号、但大于光热偏转信号[9]。

3 仿真结果及分析

假设热透镜引起的探测激光光学相移 ∆ϕ0= rad，激励光斑半径 a =200µm ，探测光波长λ=632.8nm ，聚焦透镜焦距 f=50mm ，构型参数 zx、 zy、 zD按式（9）和式（10）取值。利用式（5），可得到不同光斑尺寸的探测光在探测平面上的光强分布，结果如图3所示，其中 m 和 n 都取50以保证足够的计算精度。

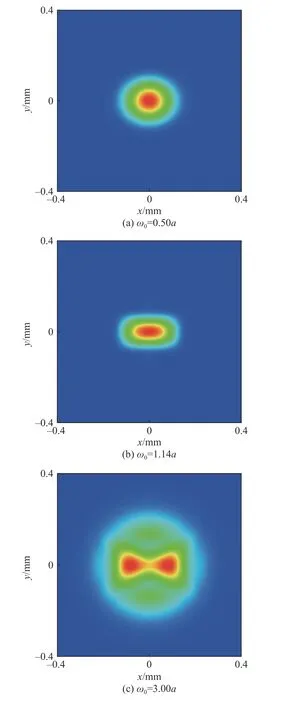
图3 不同光斑尺寸的探测光在探测平面上的光强分布Fig.3 Intensity profile of probe beam with different spot size on detection plane

当探测光光斑半径较小时热透镜近似为理想薄透镜，如图3（a）所示，探测平面上探测激光光强呈椭圆形高斯分布， x 方向光斑半径大于 y 方向的光斑半径，使得四象限探测器的2、4象限光功率大于1、3象限光功率，产生聚焦误差信号。

随着 ω0的增大，如图3（b）所示，热透镜对探测激光的衍射效应逐渐增强，探测平面上探测激光光强不再是椭圆形高斯分布，光强分布在 y方向明显变窄，而在 x 方向加宽，使得四象限探测器的2、4象限光功率进一步增大，而1、3象限光功率进一步减小，产生的聚焦误差信号增大。

随着 ω0继续增大，如图3（c）所示，探测光中心区域光强分布受热透镜衍射效应的影响愈发明显，使得四象限探测器的2、4象限和1、3象限接收到的光功率的差别进一步增大，而探测光边缘区域受热透镜的衍射效应影响较小，四象限探测器2、4象限和1、3象限接收到的光功率差别不大。随着探测光斑的增大探测平面上探测光光斑同时增大，虽然探测光斑中心区域光强分布的变化对聚焦误差信号的影响增大，但光功率占比减小，而边缘区域对聚焦误差信号基本无影响且光功率占比增大，总体可以使聚焦误差信号减小。

为进一步分析探测光斑半径对聚焦误差信号的影响并验证构型优化理论的正确性，利用式（8）计算热透镜在线性光学相移近似条件下探测光斑半径 ω0和聚焦透镜间距 Dz对聚焦误差信号的影响。设探测光最大光学相移 ∆ ϕ0=0.001 rad，满足式（8）近似条件， Dz取值范围为0～ 2 f ，ω0取值范围为0～ 3a ，其余参数与图3相同。

计算结果如图4所示：当 Dz=0 时，两柱面聚焦透镜等效为一理想薄透镜，探测平面上光强始终为圆形分布，因此 SFE−L始终等于零且与探测光斑半径 ω0大小无关；当 Dz＞0 时， SFE−L随着 ω0增大先增大后减小，与图3结果一致且与Dz的取值有关。当 Dz较小时， SFE−L随着 ω0增大变化相对比较缓慢且极大值较小；而当 Dz较大时， SFE−L随着 ω0增大先迅速增大而后缓慢减小且极大值较大。此外， SFE−L极大值对应的 Dz随着 ω0增大而逐渐减小。当 ω0≈1.14a 时， SFE−L达到最大值约为 0 .354∆ϕ0，对应的 Dz≈0.88f ，与理论结果一致。

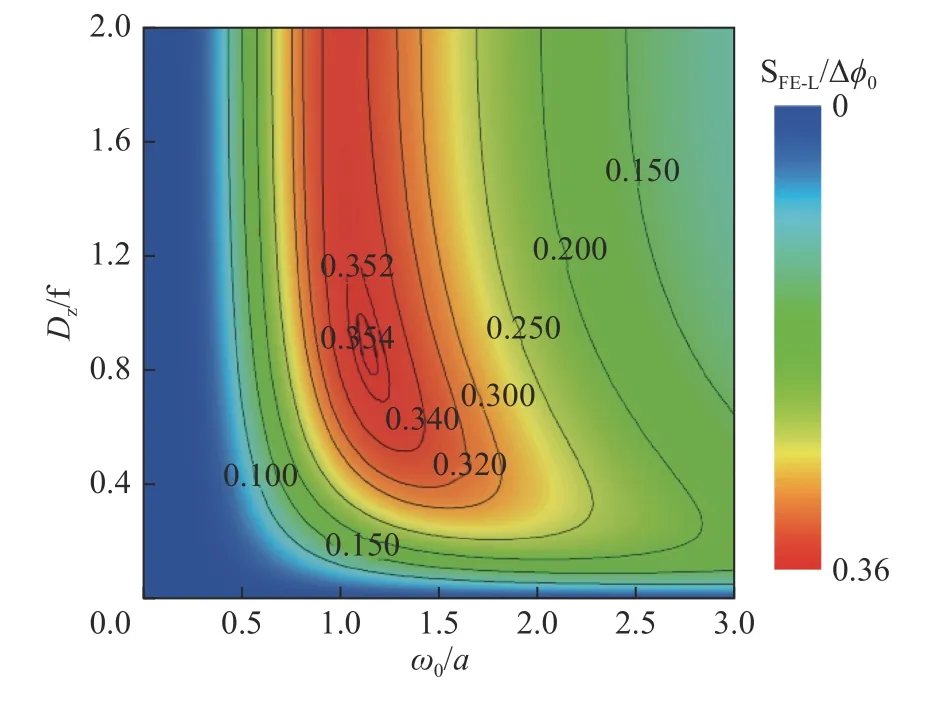
图4 聚焦误差信号随探测光斑半径和聚焦透镜间距的变化关系Fig.4 Focus-error amplitude as function of both probe beam radius and distance between two cylindrical focusing lenses

此外，探测光斑半径的变化还会影响聚焦误差信号的线性范围。利用式（7）可得到聚焦误差信号 SFE随 探测 光 斑半径 ω0和热 透 镜引起 的 探测光最大光学相移 ∆ ϕ0的变化关系，结果如图5所示，其中 ∆ ϕ0取值范围为0～2 rad，其余参数与图3相同。

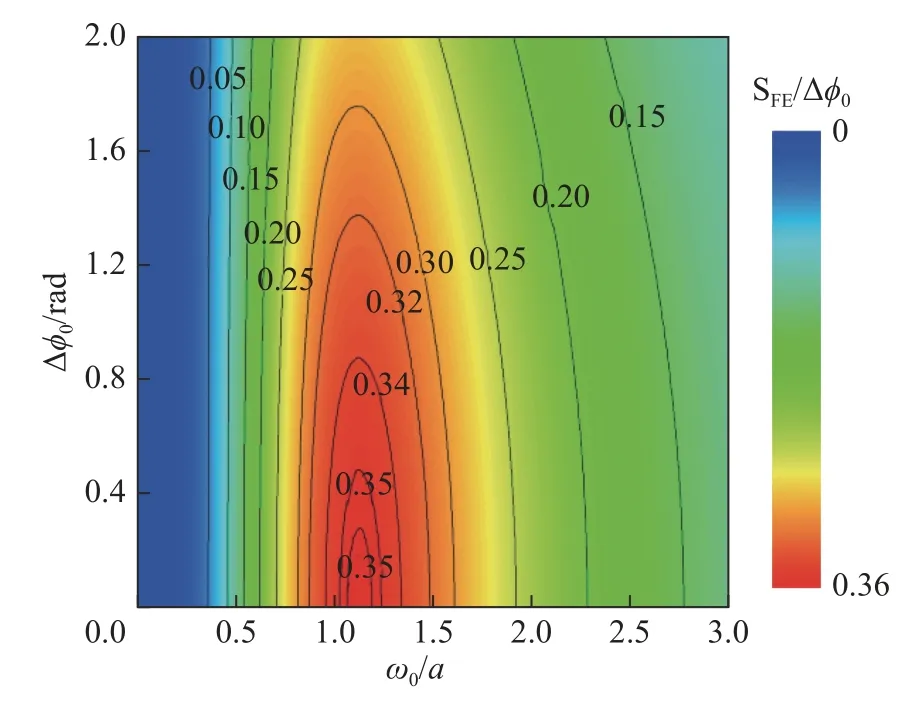
图5 聚焦误差信号随探测光斑半径和热透镜最大光学相移的变化关系Fig.5 Focus-error amplitude as function of both probe beam radius and maximum optical phase-shift of probe beam

由此可以得出：当 ω0＜0.25a 时，聚焦误差信号 SFE与探测光最大光学相移 ∆ ϕ0基本保持线性关系，线性范围大；而当 ω0＞0.25a 时，随着ω0的增大 SFE与 ∆ ϕ0呈现明显的非线性特性， SFE与 SFE−L相比有所减小，且与 SFE−L的相对差别随着 ω0增大而逐渐增大，线性范围逐渐减小。

为定量分析探测光斑对聚焦误差信号的线性范围的影响，引入非线性误差 δ ，定义为

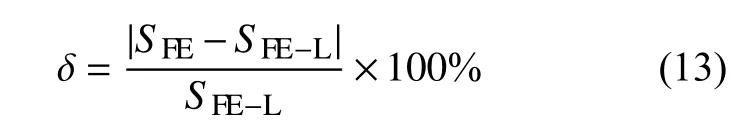
利用图5数据以及计算对应的 SFE−L得到非线性误差随探测光斑半径和探测光最大光学相移的变化关系，如图6所示。

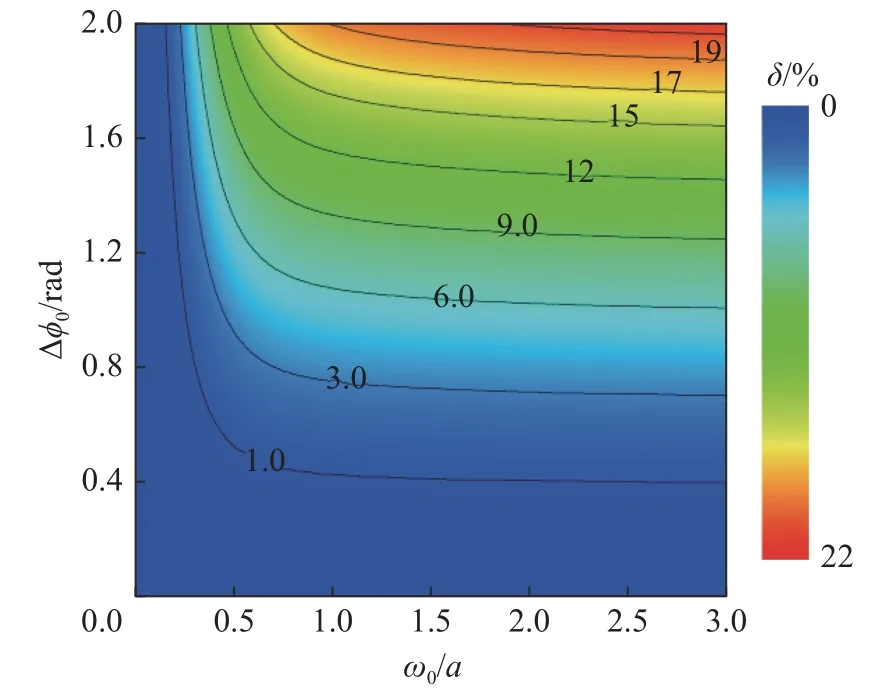
图6 线性误差随探测光斑半径和热透镜最大光学相移的变化关系Fig.6 Nonlinear error of focus-error signal as function of both probe beam radius and maximum optical phase-shift of probe beam

由图6可以看出，非线性误差随着 ω0和 ∆ϕ0的增大而增大。当 ω0＜0.25a 时， ∆ ϕ0=2 rad时的非线性误差＜4%且随着 ω0的减小而减小；当ω0从 0 .25a 增大到 a 时非线性误差从4%迅速增大到19%，即线性范围随着 ω0的增大而迅速减小；当 ω0从 a 增 大 到 3a 时 非 线 性 误 差 仅 从19%增大到21%，此时 ω0的增大对线性范围的影响较小。虽然探测光斑半径增大使得聚焦误差信号的线性范围减小，但在构型参数优化条件下∆ϕ0＜0.4 rad时的非线性误差＜1%，仍然具有较大 线性范围。

4 结 论

本文建立了基于光学相移理论的热透镜聚焦误差信号理论模型，利用该模型得到了热透镜效应条件下的构型参数优化条件及最大聚焦误差信号理论值。研究结果表明：探测光斑半径为激励光斑半径的1.14倍时，聚焦误差信号最大。通过数值计算分析了探测光斑半径对聚焦误差信号幅值及其线性范围的影响。计算结果表明：聚焦误差信号随探测光斑半径的增大先增大后减小，探测光斑半径优化值及其相应的最大聚焦误差信号与理论结果一致；而聚焦误差信号的线性范围随着探测光斑半径的增大而逐渐减小，在构型参数优化条件下探测光最大光学相移＜0.4 rad时聚焦误差信号的非线性误差＜1%。这些结论可为进一步提高热透镜聚焦误差的测量灵敏度和准确度提供参考。