基于DBSCAN-3σ的雷达去噪算法研究

张 浩，张荣福

（上海理工大学 光电信息与计算机工程学院，上海 200093）

引 言

随着现代电子科学技术的发展，微波雷达技术广泛应用于军用和民用领域，越来越多的探测设备都需要雷达技术的支持。与传统的传感器相比，微波雷达具有发射功率低、分辨率高以及穿透性强等特点。这些特点使得微波雷达技术在运动目标检测方面具有较大的优势，可以在医疗、救援搜索等[1-3]领域发挥越来越重要的作用。

微波雷达发射电磁信号时，由于多普勒效应，其回波信号会携带被测目标的运动特征。然而，由于系统本身的高灵敏度，检测目标背景仍会产生大量噪声，目标运动信息很容易淹没在背景噪声中，以致影响运动信息的特征提取，所以去噪成为发挥雷达探测能力的关键。目前，常用的去噪和数据提取算法主要有：经验模态分解算法（empieical mode decomposition, EMD）、小波变换、基于机器学习的去噪算法等。

Wang等[4]以EMD的阈值去噪算法为原型，提出了一种对雷达信号进行奇异谱约束的总体经验模态分解（EEMD）改进算法。这种方法将雷达信号分解成若干固有模态函数（IMF），通过过滤含有噪声的IMF来去噪。但经验模态分解方法存在模态混合的问题，导致时频分布严重混叠，在信噪比低时存在性能不稳定、信号失真，不能有效去噪。Nguyen等[5]结合连续小波变换和EMD算法进行去噪，从雷达回波信号中检测出短时心血管脉冲。小波变换虽然有良好的时频分辨率，但结果主要取决于小波基函数的选择，不具有很好的稳定性。Huang等[6]使用生成对抗网络（GAN）进行微波雷达回波时域图去噪，这种网络具有较强的去噪性能，能够消除各种级别的噪声，无需估计噪声强度。但是，这种方法需要大量的数据训练模型，在实际使用时可能没有较多的数据集用来训练，从而导致过拟合，去噪性能达不到最佳。

聚类算法是数据处理中的一项重要技术，它可以根据数据对象之间的相似性，将差异最小的数据对象归为一类。在雷达信号的去噪中，可以利用聚类分析的特殊性来弥补传统去噪方法的不足。而通常的聚类算法（如k-mean均值聚类算法等）仅适用于样本数据分布相对规则的情况；且需要预设或假设雷达噪点的个数，一旦雷达噪点个数预设不正确将对去噪效果产生严重的影响。本文在研究雷达检测目标位移回波信号的基础上，提出一种结合DBSCAN（density-based spatial clustering of applications with noise）聚类算法和拉依达准则（3σ）去噪方法，并通过雷达实测数据进行验证。

1 基于CW雷达的检测系统

雷达是一种无线电检测技术，主要包括脉冲雷达和连续波雷达。其中脉冲雷达有瞬间的功率变化且功率变化大，硬件成本较高，一般用于远距离目标的检测中。连续波雷达主要分为单频连续波（continuous wave, CW）雷达、调频连续波（frequency modulated continuous wave, FMCW）雷达等。雷达检测系统可对目标进行非接触式检测，提高雷达发射频率可以检测目标的运动状况，采用连续波这种方法可探测到目标毫米级的运动，适合于近距离的位移测量。图1为CW雷达检测系统原理框图。信号处理单元控制雷达前端产生发射信号，通过发射天线（TX）发出。接收天线（RX）接收回波信号，模拟信号处理电路（ASP）对回波信号进行处理，并使用模拟数字转换器（ADC）将处理后的模拟信号转换为数字信号，数字信号再经信号处理单元提出信号中所需要的信息，最终结果由外围设备进行显示。

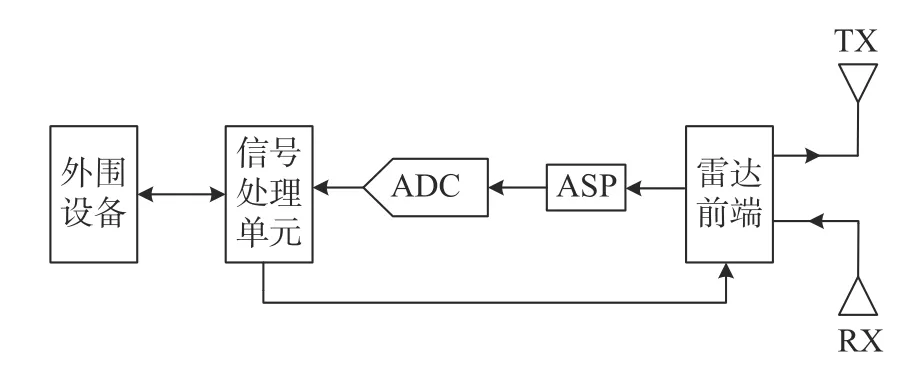
图1 雷达原理框图Fig.1 Block diagram of radar principle

本文在采集数据的雷达前端使用等幅正弦波发射，采用零中频接收机结构，雷达载波工作频段为24 GHz。为节省体积，收发天线采用微带贴片天线。模拟信号处理电路主要实现信号的放大滤波和电平搬移，模数转换使用24 bit高精度ADC。信号处理单元用于数字信号处理和调控各级联单元的工作，同时信号处理单元与外围设备相连。信号处理单元一方面实现检测结果的输出，另一方面实现用户对控制信号输入，设置系统各种参数等功能。

CW雷达一般采用正交接收机，这样可以产生同相和正交（I/Q信道）信号输出。正交接收机的原理如图2所示。发射天线发出的恒频连续波可表示为

图 2 正交接收机原理图Fig. 2 Principle diagram of quadrature receiver

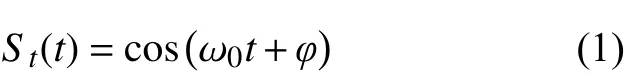
式中： ω0是发射波的圆频率； φ 是初相位。

如果被测目标到雷达的径向距离为 d ，则接收天线收到的回波信号可表示为

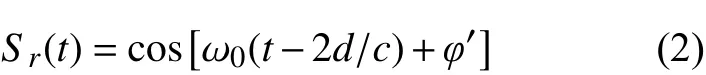
式中： φ′是在初相位的基础上叠加了半波损失和其他相位损失后的相位部分； c 是光速，表达式中的振幅采用了归一化表达。

在正交接收机中，本振信号进入正交解调器中，然后输出相位差为90°的同源信号。雷达回波信号通过低噪声放大器（LNA）放大，变为输出功率相等的两路信号，这两路信号分别与相位差为90°的同源信号混频并滤波，得到以下两路基带信号：

在实际测量环境中，可能会有静止物体、杂波以及其他运动物体的回波干扰，为简单起见，可以只考虑固定物体和固定杂波的干扰。对于这种干扰，混频的信号是一个直流信号，相当于在式（3）和式（4）的基础上增加了固定的直流分量I0和 Q0。由于两路基带信号来源于两个通道，很难达到理想的等幅正交，需考虑直流分量和振幅的不平衡。在有干扰情况下，基带信号的表达式为：

根据三角函数关系， I (t) 、 Q (t) 满足方程

由式（7）可以看出 I (t) 、 Q (t) 的合成轨迹是一个椭圆。通过椭圆拟合算法可以得到 I0、 Q0、A 、 B 的值，进而求出输出信号的相位，即

假如初始时刻的相位为 φ0，末时刻的相位为 φ1，则可通过初末时刻的相位差得到目标的位移变化，即

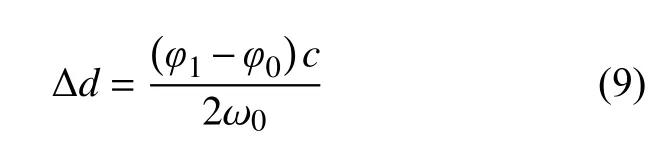
由式（9）可知，相位与障碍物的位置有关，通 过相位变化可以反映目标的相对位移变化。

2 基于DBSCAN-3 σ 的去噪算法

2.1 DBSCAN聚类算法

在雷达回波信号的处理过程中，回波信号的去噪是重要一环。由上述可知，两路基带信号（利用最小二乘法）合成的轨迹为椭圆，这两路信号的反正切值即为相位信息。但由于回波信号中有噪声的影响，两路基带信号仍会出现幅度失衡和相位失衡的情况，拟合的椭圆也会有误差，因此在椭圆拟合之前需要对原始雷达数据进行去噪处理。本文提出DBSCAN-3σ的去噪算法：首先利用DBSCAN聚类算法将雷达数据进行分类，由于噪点一般是随机出现且时间较短，因此聚类结果中的不属于任何簇的离群点即为噪点；然后基于拉依达准则对剩余数据点进行处理，将幅度较小的噪点分辨出来；最后将去噪后的数据用最小二乘法进行椭圆拟合，根据式（9）得到目标的位移信息。

定义6（边界点）：对 xj∈D ，如果 xj不是核心点，但是 xj由核心点密度可达，则 xj为边界点。

定义7（类簇和噪声）：从数据集 D 中任取一点 p ，从 p 点开始在 D 中搜索满足Eps和MinPts条件且密度可达的所有点构成一个簇，不属于任何簇的点则被标记为噪点。

基于上述概念，DBSCAN算法的核心是：在数据集中任选一点 p 作为起始点，根据Eps和MinPts，查找所有从 p 点密度可达的点；如果是核心点，那么在Eps邻域内的所有候选点为一个簇，然后通过考察候选点的密度来进一步扩大这个簇，直至最终完整的簇被找到；如果 p 不是核搜寻心完点毕，，则数继据续中搜不寻属下于一任个何点簇，的直点至即所为有噪的点点[都9]。

2.2 拉依达准则

拉依达准则是以三倍观测值的标准差 σ 作为极限取舍的标准，因此拉依达准则也被称作 3σ准则。标准差 σ 为经过大量重复观测后计算出的参数，其计算式为

2.3 基于DBSCAN-3 σ 的椭圆拟合算法

本文去噪方法可以分为两步：首先要设置聚类参数，对雷达原始数据进行DBSCAN聚类，根据密度特征会将数据分为若干不同的簇，去除不属于任何簇的噪点；然后根据拉依达准则去除影响较大的奇异值。根据去噪后的结果，对数据进行椭圆拟合，计算去噪后的线性误差和线性度。为了验证算法的有效性，利用半径滤波算法与本文算法进行对比。算法流程图如图3所示。

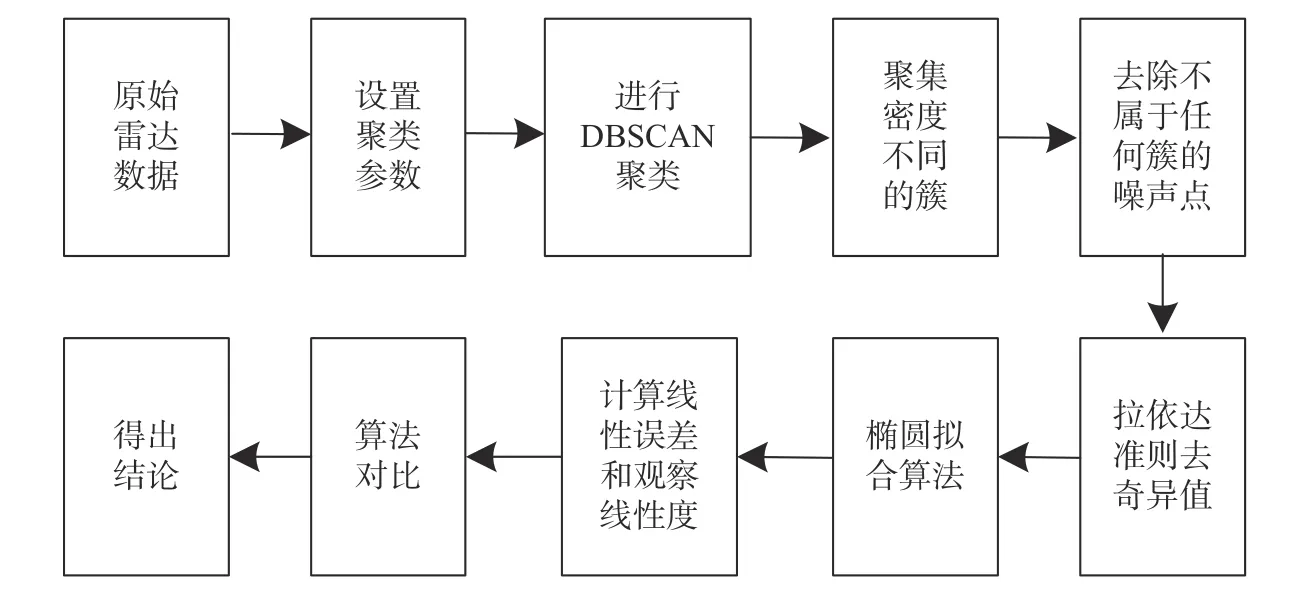
图3 算法流程图Fig.3 Flow chart of the algorithm

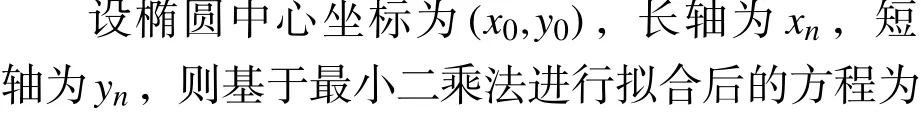
式中n是采集数据点的总数。

式（13）中 ( xi,yi) 为曲线上任一点，则雷达数据集中各点到椭圆曲线的欧式距离为

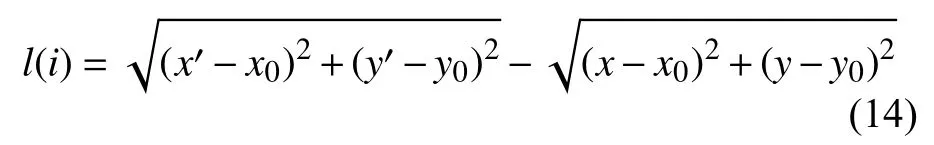
该组数据点的算术平均值可表示为

残差为

若残差 lb(i) 位于 [−3σ,3σ] 外，则进行第二次筛选，将其认为噪点并剔除。

重复以上步骤直至所有的点都在 I ¯+3σ 范围以内为止。

3 实验结果与分析

3.1 实验结果

本文以CW雷达为实验平台采集实验数据，使用的雷达传感器为ADI公司的ADF4158芯片和Infineon公司的BGT24MTR芯片组成的毫米波雷达模块，工作频率为24 GHz，能够提供毫米级的距离分辨率。雷达采用微带贴片天线收发信号，DC电源为雷达提供直流电。NI公司的PXI-4461高精度数据采集模块负责数据采集，然后将信号输入到计算机中，使用本文提出的算法并采用MATLAB软件进行处理。

图4 为实验环境和设备，在步进电机上固定一块金属反射板作为被测目标，控制步进电机的运动方向垂直于雷达的收发天线。反射板初始时刻距离雷达天线80 cm，控制步进电机以20 mm/s的速度匀速运动80 mm。数据采集卡接收到的信号传输到计算机上，经过正交接收机，基带信号输出为I/Q两路，将这两路信号在垂直方向上进行叠加。图5是采集到的原始数据，其中：（a）显示了I/Q两路信号合成轨迹图及椭圆拟合；（b）为反射板随时间位移图；（c）为相对位移的误差分布图。由图5可知，椭圆主体的采样点即为雷达采集到反射板运动的数据，但采样点中含有较多杂散的噪点，使得拟合出的椭圆发生形变，对计算目标的相对位移产生了影响，导致（b）中的线性度较差，有明显的起伏，并使（c）中的反射板相对位移的最大线性误差也达到了12 mm。

图4 实验环境与设备Fig.4 CW radar module and dual rail module

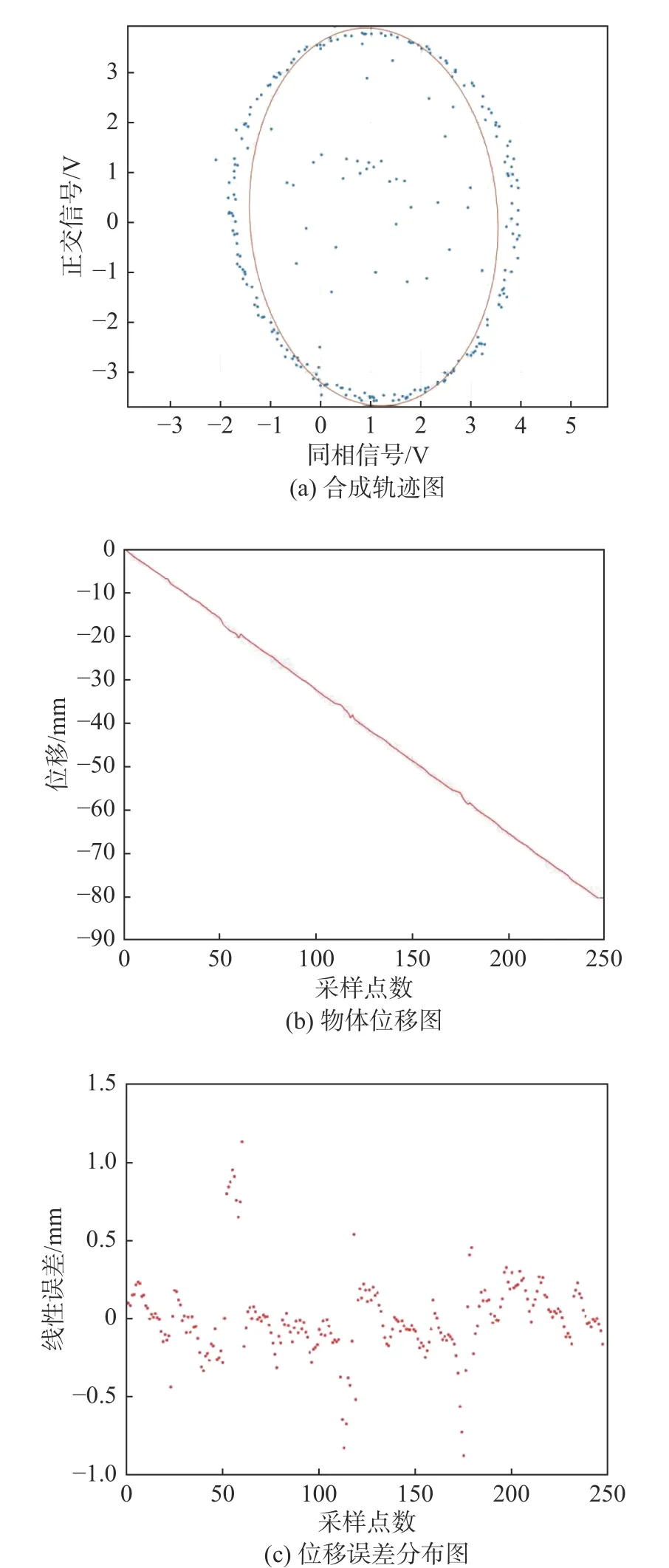
图5 原始数据图Fig.5 Raw data

利用上述算法，对雷达测量的原始数据进行处理。在DBSCAN聚类算法中，将Eps设为0.3，MinPts设为4时聚类情况较好。图6为雷达数据聚类图，从图中可以看出，根据密度不同将数据点分为颜色不同的五种聚类群，空白的点是不属于任何簇的噪点，可见椭圆内部大量的噪点已经被去除。

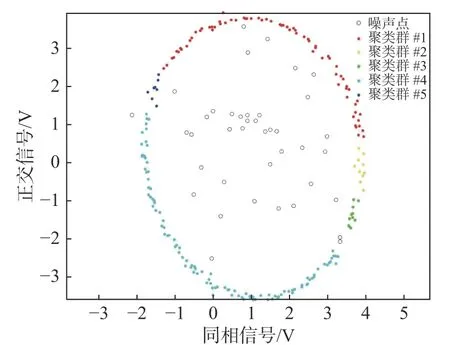
图6 雷达数据聚类图Fig.6 Clustering graph of radar data

经过DBSCAN-3σ算法处理，噪点基本已经被去除。将处理后数据进行椭圆拟合，计算其相对位移和线性误差，结果如图7所示。由图7可知，经过聚类算法和拉依达准则去噪后的拟合效果优于去噪之前，见（a）图；物体随时间位移图像较原始数据更加平滑，线性度更好，见（b）图；图中去噪后的线性误差极值要远小于之前，线性最大误差从12 mm降低到0.36 mm，明显消除了噪声对数据的干扰，见（c）图。

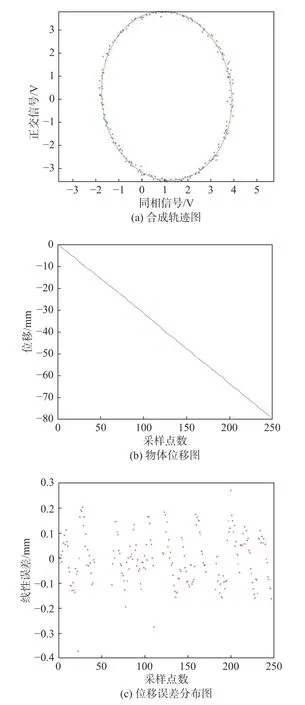
图7 DBSCAN-3σ去噪结果图Fig.7 DBSCAN-3σ denoising result

3.2 算法对比

半径滤波算法也是常用的去噪算法，其原理是假设数据中每一个点在给定的半径Eps内至少存在MinPts个点，符合假定条件的点作为信号点保存下来，不符合条件的点作为噪点除去，其中半径Eps以及数值MinPts由人工指定。观察半径滤波结果，并与本文去噪算法结果进行比较，去噪后数据如图8所示。

由图8可以发现，半径滤波的结果起伏非常大，半径滤波对悬空的孤立点或无效点具有很好的去除效果，但对于聚集的噪点，其去噪准确性相对于DBSCAN-3σ算法较低。

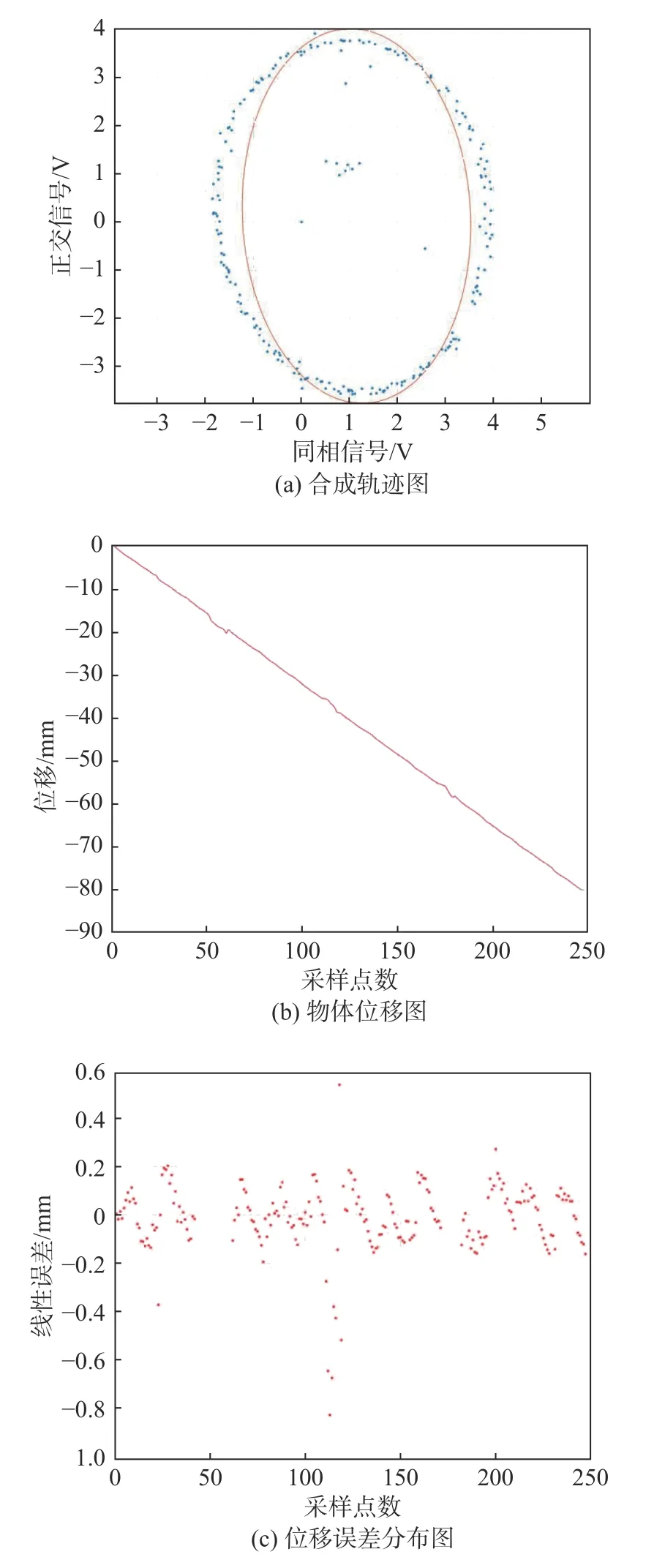
图8 半径滤波结果图Fig.8 Radius filtering result

3.3 算法特性分析

DBSCAN-3σ去噪算法是根据信号与噪声之间的密度不同来进行去噪。对于DBSCAN聚类算法，其时间复杂度取决于确定Eps和MinPts后且查找Eps领域中的点所需要的时间，所以DBSCAN算法的基本时间复杂度为O（N*Eps领域扫描点所需要的时间，其中N为扫描点的个数）。在设置参数不合理的情况下，Eps领域需要扫描雷达数据中所有的点，最坏情况的时间复杂度为O（N2）。对于3σ准则剔除离群噪点，时间复杂度为O（N）。因此DBSCAN-3σ算法时间复杂度为O（N2）。而对于半径滤波算法，需要假设数据中的各个点在给定的范围Eps内至少有MinPts的近邻点，所以时间复杂度也为O（N2）。DBSCAN-3σ算法相较于半径滤波算法具有相同的时间复杂度，经过实验验证，该算法在去噪结果的准确性上优于半径滤波算法且计算复杂度低，对于动态信号去噪具有很好的实时性。

雷达的噪声包含静止物体杂波和运动物体杂波，其中静止物体杂波对于检测影响较小。运动物体杂波主要是人为干扰，相较于探测目标的运动信号，运动物体杂波信号出现的时间较短，在时域图中密度稀疏。DBSCAN-3σ算法不需要事先知道噪声的数量和来源，只根据噪声和信号的密度不同去噪，所以该算法对雷达在复杂环境中去噪具有很好的稳定性。

4 结 论

本文提出了一种连续波雷达的DBSCAN-3σ去噪算法，该算法基于信号和噪声之间的密度不同来进行去噪，因此具有很好的可行性。通过实验验证，该算法对噪声有很好的剔除效果，提高了雷达在检测的准确度，证明了该方法在原始雷达信号处理上可以获得更好的降噪效果。