基于CSMC 模型的电网规划指标相关性计算

谢瀚阳，彭泽武，杨秋勇，蔡雄，温柏坚

（广东电网有限责任公司，广东广州 610106）

电网建设过程中，对于电网进行有效、准确规划能够确保电网建设过程中资金的合理、充分利用以及电网运行应用的安全、稳定与经济性[1]。作为电网建设的基础，电网规划工作具有高度复杂性，这种高度复杂性主要体现为电网规划指标的不确定性、相关性以及专业性[2]。准确分析电网规划指标间的相关性可降低电网建设过程中的计算误差，提升电网建设工程的稳定性与经济性。

电网规划指标相关性主要描述电网规划中单个节点指标的时间相关性与多个节点指标之间的空间相关性[3-4]，两者分别体现节点相邻时刻指标状态之间的相关性和不同节点指标数据间的相关性[5]。连续状态马尔科夫链模型（Continuous Slate Markov Chain，CSMC）能够体现时间离散但状态连续的无记忆随机过程，能够基于相邻时刻状态间的相关性获取下一时刻状态的概率抽样值[6]。由于Copula 函数对于电网规划指标的分布模型无特殊限制，因此可依照Copula 函数特征拓展CSMC 模型。作为处理多元随机变量相关性的数学方法，Copula 函数具有高度灵活性，其利用多元随机变量联合概率分布函数的构建确定多元变量间的相关性[7]。基于此，提出基于CSMC 模型的电网规划指标相关性计算方法，从电网规划节点指标的时间与空间两方面准确计算电网规划指标的相关性。

1 电网规划指标相关性计算方法

1.1 构建多元指标一阶CSMC模型

根据电网规划指标边缘分布函数（概率分布特征）、节点指标空间与时间的相关性，综合多元指标概率分布模型与CSMC 模型能够设计一个可同时分析电网规划指标空间与时间相关性的多元指标CSMC 模型。

用Q表示电网规划节点数量，存在Q个电网规划节点的指标向量，通常既包含时间方面单个电网规划指标序列自身的相关性，也包含空间方面Q条时序电网规划指标波动曲线间的相关性。

用x1,t,x2,t,…,xQ,t,t=1,2,…,T，表示Q个电网规划节点相对的时序指标数据。利用CSMC 模型分别描述不同电网规划节点指标；利用F(·)=F1,F2,…,FQ和F′i=P(Xi,t+1≤xi,t+1|Xi,t=xi,t)分别表示对应的边缘分布函数和条件概率分布函数，X=(Xt,Xt+1) 表示随机电网规划指标构成的二维随机向量，由此可将多元指标一阶CSMC 模型表示为：

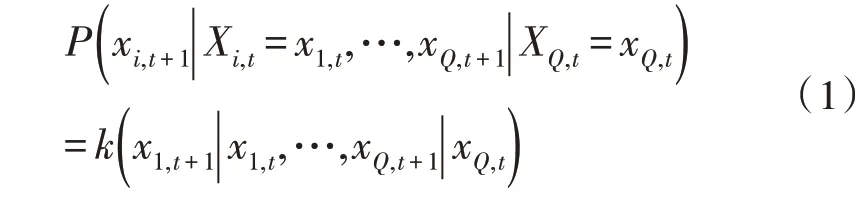
式（2）描述多元指标一阶CSMC 模型内的状态转移核：

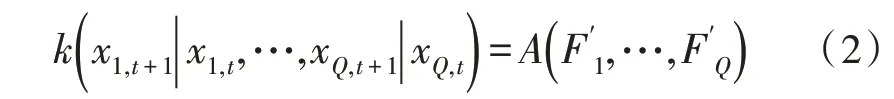
式（3）描述多元指标一阶CSMC 模型内的状态转移密度：

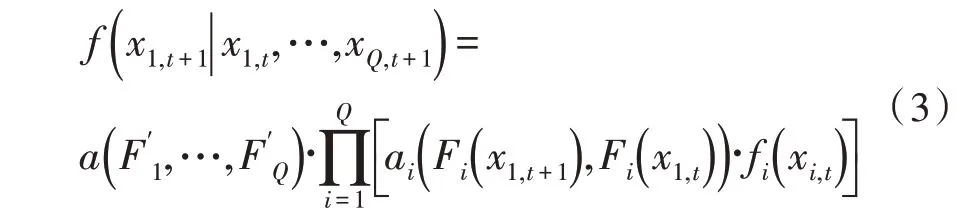
其中，A表示Copula 函数，a和ai分别表示Q个电网规划节点时序指标相关性模型相应的Copula函数密度函数和不同电网规划节点的时序指标序列Xi,t，在时间t+1 与t时刻间时间相关性模型对应的Copula 函数密度函数。

由于电网规划指标相关性计算过程中只考虑单个电网规划节点的两个指标空间相关性，对于电网规划指标的时间相关性也仅计算一阶情况[8]。因此上述多元指标一阶CSMC 模型能够简化为：

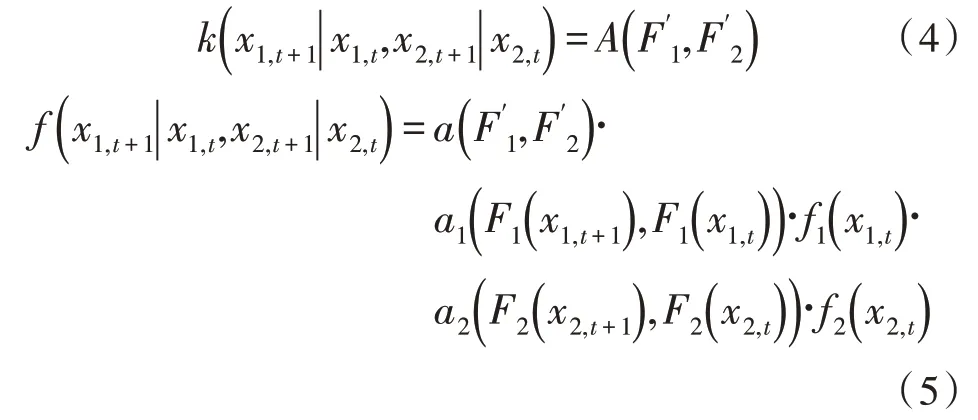
根据式（4）和式（5），能够得到状态转移核与状态转移密度，能够描述电网规划节点指标一阶CSMC模型。由此确定相邻时刻下电网规划指标状态相关性的最优Copula 函数成为求解状态转移核与状态转移密度的核心。

1.2 边缘分布函数与Copula函数的确定

1.2.1 边缘分布函数的确定

通过Matlab 构建任一电网规划指标波动数据的频率直方图[9]，分别计算其偏度值与峰度值，根据计算结果能够确定该电网规划指标分布情况与正态分布相比具有峰尖尾厚的特点，对该电网规划指标分布情况实施柯尔莫可洛夫—斯米洛夫检验[10]，确定其不具备正态分布特征，因此选取核密度估计法确定电网规划指标边缘分布函数。用f(x)表示随机电网规划指标X的概率密度函数，式（4）描述其核密度估计过程：

柑橘缺磷症状。老叶逐渐变成古铜色、紫色、无光泽，有时出现枯斑。新叶小、浓绿、发暗。枝梢纤细，春季开花期和开花后老叶大量脱落，花少，果皮粗厚。

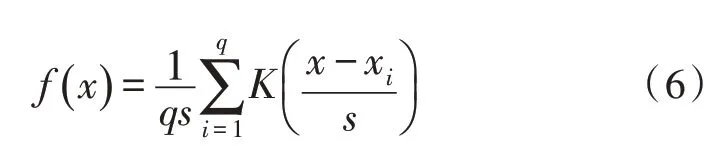
其中，q、s和K(·)分别表示电网规划指标X的样本数量、窗宽和核函数。

利用式（4）确定核密度f(x)后，对f(x)实施积分处理[11]，由此能够确定电网规划指标x的边缘分布函数F(x)。利用分布函数K(·)的累积过程实现边缘分布函数F(x)与均匀分布C之间的转换，针对均匀分布系数b∈(0,1) 存在式（5）所描述的关系：

1.2.2 Copula函数确定

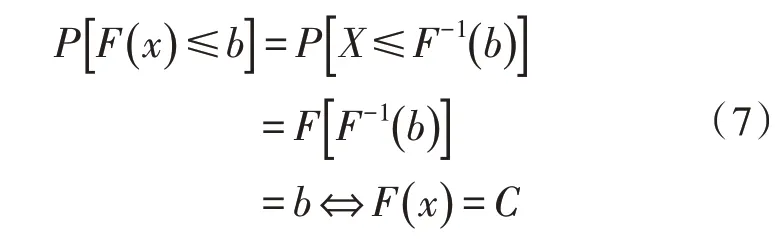
Copula 函数的选取以电网规划指标间相关性的特点为依据[12]。利用Matlab 构建任一电网规划指标波动数据的二元频率直方图，当电网规划指标X与电网规划指标Y的二元频率直方图之间呈现分布不对称状态时，可选取Gumbel-Copula 函数和Clayton-Copula 函数[13]；当X与Y的二元频率直方图之间呈现分布对称状态时，可选取Frank-Copula 函数、Normal-Copula 函数和t-Copula 函数。

选取分布极大似然估计法估算Copula 函数的相关参数。用u=S(x)、s(x)和v=R(y)、r(y)分别表示电网规划指标X、Y的边缘分布函数和概率密度函数，fxy(xy)和(xi,yi)i=1,2,…,q分别表示联合概率密度函数和样本点。根据联合分布函数的密度函数计算公式与极大似然定义确定似然函数表达式如下[14]：

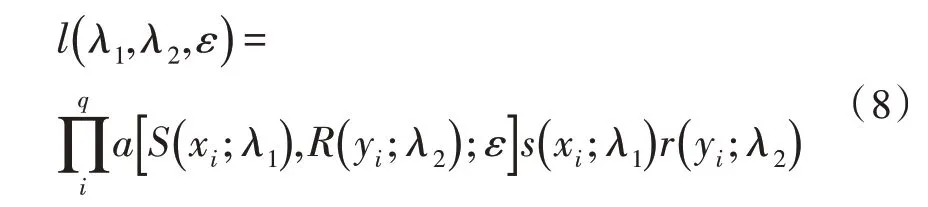
其中，λ1、λ2表示边缘分布内的未知参数。对式（8）两边取对数，得到：

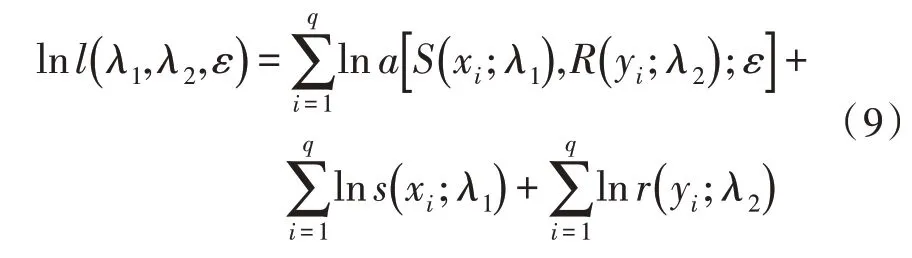
根据式（9）能够得到似然函数表达式对数值，利用两阶段极大似然估计法能够估算ε值[15]：

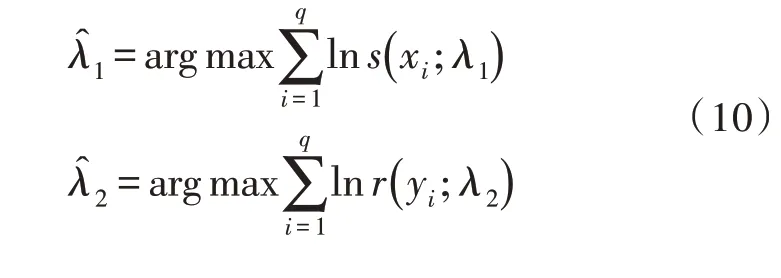
将式（10）计算结果代入式（11），获取ε极大似然值：

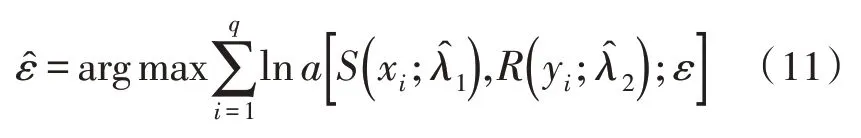
根据得到的Copula 函数求取相应的状态转移核或状态转移密度。

2 实验分析

为验证文中提出的基于CSMC 模型的电网规划指标相关性计算法的计算性能，以我国某省电网规划工程为研究对象，以电网规划常用指标变压器平均负载率（体现电网运行的经济性）与用户端电压合格率（体现电网运行的稳定性）为计算指标，利用文中方法计算两个指标之间的相关性[16]。表1 为两个计算指标的初始数据。

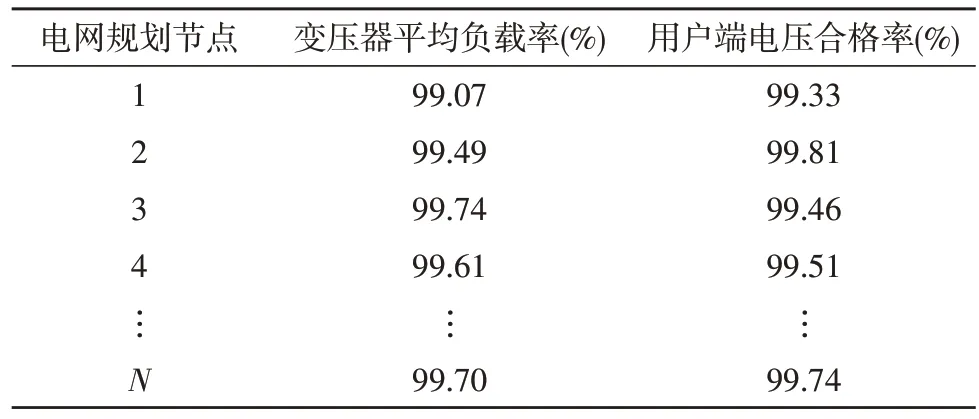
表1 计算指标的初始数据

2.1 确定指标边缘分布

文中方法电网规划指标边缘分布确定所采用的核密度估计法为一种非参数估计法，可在无分布先验知识与概率分布形式的基础上，基于指标数据样本分析指标特征，利用经验分布法确定分析精度。基于表1 中两个计算指标的原始数据，采用文中方法确定两个指标的边缘分布结果S(x) 和R(y)，以经验分布函数为指标（经验分布函数为指标实际边缘分布函数的逼近），判断文中方法确定的两个计算指标边缘分布结果的精度，判断结果如图1所示。

图1 中，较细的实线与较粗的虚线分别表示经验分布函数与文中方法确定的指标边缘分布结果。由图1 可知，文中方法确定的两个计算指标边缘分布结果与经验分布函数基本重合，由此说明文中方法基于指标原始数据能够准确地分析两个计算指标特征与规律。

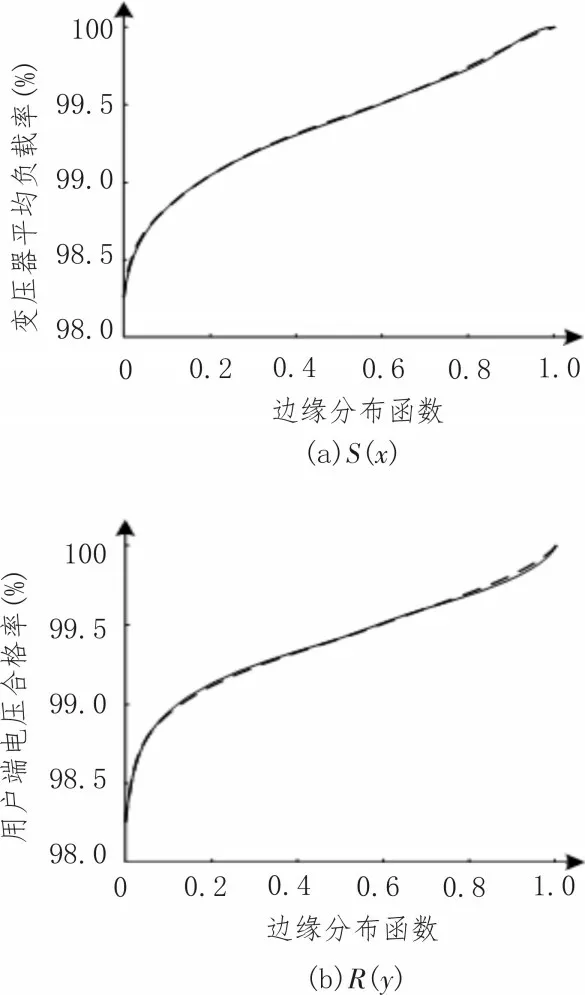
图1 文中方法对于指标边缘分布结果的计算精度

2.2 确定Copula函数

确定两个计算指标的边缘分布函数后，利用Matlab 编程确定两个计算指标的二元频率直方图，依照该直方图确定合适的Copula 函数。

基于表1 中两个计算指标的初始数据以及文中方法所用的分布极大似然估计法，能够计算出二元Normal-Copula 函数与二元t-Copula 函数内未知参数值，如表2 所示。

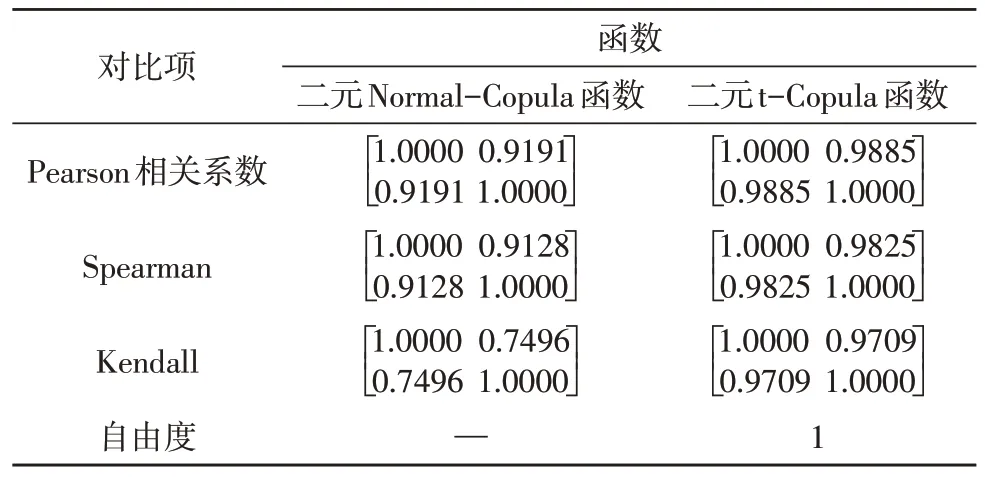
表2 候选函数内未知参数计算结果

由表2 可知，二元Copula 函数内的未知参数值分别为0.919 1、0.988 5 和1。

以经验Copula 函数为指标能够计算出两个候选二元Copula 函数同经验Copula 函数之间的平方欧氏距离，根据平方欧氏距离能够确定文中方法所用Copula 函数。

2.3 应用性能测试

为测试文中系统的应用价值，在PSS/E 交互式电力系统仿真程序中，利用文中方法对研究对象的电网规划指标相关性计算结果进行仿真，计算其变压器平均负载率与用户端电压合格率，与表1 中两个计算指标的初始数据相对比，结果如表3 所示。

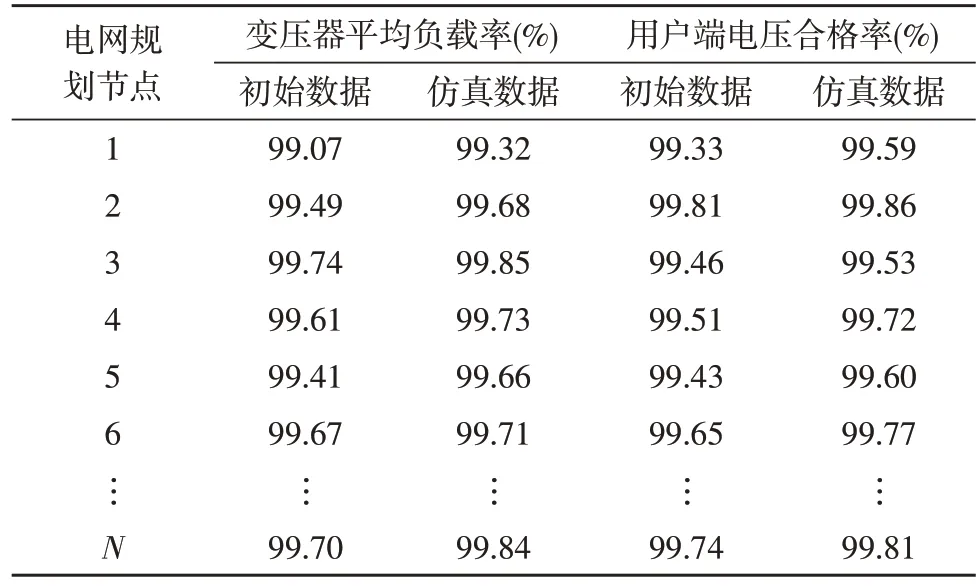
表3 计算指标的变化情况

分析表3 能够得到，研究对象基于文中方法电网规划指标相关性计算结果进行规划建设后，其不同节点的变压器平均负载率与用户端电压合格率均呈现不同幅度的上升趋势，由此说明利用文中方法可提升电网建设工程的稳定性与经济性。

3 结论

电网规划指标间的相关性直接影响电网工程运行的有效运行。文中提出基于CSMC 模型的电网规划指标相关性计算方法，从Copula 函数为基础，利用CSMC 模型从时间和空间两方面准确计算电网规划指标的相关性。由于文中方法指标相关性计算只针对两个指标进行计算，因此在后续研究中将针对多指标相关性的计算进行研究。