考虑连接性的三明治阻尼复合结构拓扑优化设计
张 横 丁晓红 沈 磊 徐世鹏
上海理工大学机械工程学院,上海,200093
0 引言
航天航空、航海等工程装备日益向高速重载方向发展,三明治结构由于具有多功能性的特点被广泛应用于这些工程装备中。这些工程装备在工作中经常承受动态载荷,容易引发结构振动噪声问题,如潜艇的隐身性能与舰体的振动噪声息息相关,减小舰体的振动噪声可以有效提高潜艇的隐身性能。为保证这些装备能够正常有效工作,通常要将结构的振动水平控制在某一范围内。结构振动控制通常采用主动控制和被动控制方法。被动控制方法由于其可靠性高、可控频带宽等优点,成为结构振动噪声控制的有效方法,其中在结构上施加阻尼材料,通过提高结构阻尼来达到减振目的是一种行之有效的措施。另外,结构还需要保证高刚度特性,以满足承受载荷的需求。
三明治阻尼复合结构的宏观性能与中间阻尼层材料的性能息息相关,针对高刚度高阻尼的设计要求,有效且直接的方法是设计阻尼复合材料的微结构。为了实现高刚度高阻尼,阻尼复合材料在微观结构上可由两相材料组成,一相为刚度较大的材料,用于保证结构的刚度,另一相为阻尼较大的材料,用于提高结构的阻尼。通过对这两相具有竞争性的材料进行拓扑优化设计,可以得到高刚度高阻尼的三明治阻尼复合结构。
针对材料微结构设计问题,SIGMUND[1-2]提出了基于逆均匀化方法的材料微结构设计方法,实现了材料特定刚度和负泊松比设计。对于阻尼复合材料的设计,YI等[3-4]研究表明,微观拓扑形态的改变可以提高黏弹性复合结构的刚度和阻尼性能,并通过将逆均匀化方法[1-2]应用于阻尼复合材料的设计中,实现了以提高阻尼复合材料刚度和阻尼性能为目标的微结构设计。ANDREASSEN等[5]针对阻尼复合材料不同的微结构形式对材料的带隙特性的影响进行了研究。CHEN等[6]对阻尼材料剪切模量和阻尼因子之间的关系进行了研究,并通过对剪切模量进行优化设计,来提高结构阻尼。ANDREASEN等[7]以提高结构阻尼性能为目标对黏弹性复合材料的微结构进行了优化设计。HUANG等[8]研究了阻尼复合材料设计中目标问题,对比了分别以刚度和阻尼为设计目标时微结构的构型问题。
针对以结构宏观性能为目标的微结构设计问题,CHEN等[9]分别以结构第一阶阻尼比、第二阶阻尼比、第三阶阻尼比和前三阶加权阻尼比加权和为目标对约束阻尼层结构的微结构问题进行设计研究,结果表明,在这4种设计目标下,当体积分数为0.4和0.5时微结构的构型基本相同。YUN等[10]针对动态载荷作用下三明治阻尼复合结构中的阻尼层进行了微结构优化设计研究,设计结果表明,进行微结构设计后整体结构的振动响应大幅减小。LIU等[11]在考虑结构频率约束情况下对阻尼复合结构的微结构进行了设计,优化后结构的振动响应相较于经验设计明显减小。ZHANG等[12]研究了阻尼复合结构的多尺度设计问题,研究表明阻尼复合材料可以有效提高结构阻尼、减小振动响应。
尽管对阻尼复合材料进行微结构设计可以有效提高材料阻尼性能,达到减振的目的,但是通常以阻尼为目标的阻尼复合结构设计中[4-5,7-8,12],都是阻尼较大相材料保持连接性,刚度相被分割为孤岛,这主要是因为阻尼相连接能保证结构的虚部较大、实部较小,从而可以有效提高结构的阻尼,但是这种结构不利于后续的加工制造。ANDREASEN等[5]研究发现,通过刚度约束并不能保证微结构的连接性。HUANG等[8]研究表明,以阻尼因子为目标可以有效提高材料阻尼性能,微结构中阻尼材料保持连接性;而以刚度为目标可以保证微结构中刚度相材料保持连接,但是微结构的阻尼性能较差。
为了提高结构的可制造性,需要研究考虑制造约束的三明治阻尼复合结构的设计方法。针对连接性设计问题,ZHOU等[13]采用强制性连接约束法、虚载荷法和非线性扩散法针对单相材料进行了设计和比较,由于是单相材料,微结构构型的连接性变化对设计目标的影响较小;对于由性能相反的两相材料构成的微结构而言,材料的构型变化对目标函数和设计约束有很大的影响,无法直接采用上述方法解决微结构的连接性约束设计问题。本文提出通过组合强制性约束法和非线性扩散法的新方法,来实现具有刚度相连接的两相材料阻尼复合结构的最大阻尼设计。
1 三明治阻尼复合结构计算模型
为实现三明治阻尼复合结构的连接性优化设计,需要首先建立三明治阻尼复合结构的计算模型,并进行有限元分析。
1.1 三明治阻尼复合结构
为了确保结构的可加工性要求,需要对结构中易加工相材料进行连接性约束设计。两相材料分别为铝合金和环氧树脂,在三明治阻尼复合结构制造中,可事先将铝合金部分通过3D打印或者其他方式加工出来,然后将另外一相浇筑进去,即可得到最终的三明治阻尼复合结构。图1a所示为三明治结构,其中,中间层为阻尼层,上下层为金属层。对阻尼层进行微结构设计,使微结构中刚度相材料与上下表层相连接,这样可以整体打印出上下表层及阻尼层的刚度相材料,最终得到图1b所示的连结性结构。

(a)三明治结构

(b)连接性刚度相材料图1 三明治结构及其连接性描述Fig.1 Sandwich structures with connectivephase material
1.2 结构模态阻尼比的计算
阻尼材料的阻尼特性使用复模量表示,公式如下(本文不考虑阻尼材料性能随温度和频率而改变特性的情况):
E=E′+jE″=E′(1+jη)
(1)
式中,E′、E″和η分别为黏弹性材料的储能模量、损耗模量和材料损耗因子;j为虚数单位。
结构自由振动的运动微分方程为

(2)
其中,u为位移向量,M和K分别是结构质量矩阵和刚度矩阵,由于阻尼材料模量的复数形式,可知K为复刚度矩阵,表达式为
K=Kp+Kv=KR+jKI
(3)
这里,Kp和Kv分别为上下金属层和阻尼层的刚度矩阵。上角标“p”和“v”分别代表金属层和阻尼层。KR和KI分别为复刚度矩阵的实部和虚部,其表达式分别如下:
KR=Kp+ReKv
(4)
KI=ImKv
(5)
基于模态应变能法[14]计算结构的第k阶模态阻尼比可表达为
(6)

2 优化数学模型及灵敏度分析
2.1 连接性约束
以阻尼为目标的设计通常都会得到高阻尼材料相互连接的结构,但是这样的结构很难制造。考虑到微结构中刚度相材料的连接性,通过组合强制性连接约束法和非线性扩散法实现。强制性连接约束通过选定部分非设计域来实现,三明治结构上下表层与阻尼层中刚度相材料连接,考虑将单胞的四角点作为强制性连接约束的非设计域,如图2所示。

图2 强制性连接约束示意图Fig.2 Schematic of kinematical connectiveconstraints method
非线性扩散可以有效抑制棋盘模式和模糊边界,确保适当的拓扑互连。从理论上讲,密度梯度发生在材料交界处,因此,最小化密度梯度的范数可以有效避免非连接的发生。非线性扩散方程可以表示为
∂tx=div(D×x)
(7)
式中,D为扩散张量;x为对应的质量浓度,也就是材料密度;t为尺度参数,如时间系数。
扩散过程的性质由扩散张量决定,当D为单位矩阵时,扩散过程沿四周均匀进行,如热传导方程;当D是结构密度差分的函数形式时,就形成了非线性扩散:
∂tx=div(g(|x|2)x)
(8)
其中,g(│x│2)为扩散函数,引入一个势函数,使其梯度与扩散函数有如下关系:
φ(|x|)=g(|x|2)x
(9)
在变分法中,非线性扩散可以被描述为能量的形式,因此,形成非线性扩散方程的能量泛函最小化可以表示为

(10)
其中,Y为微结构的设计域。为使结构内部连续性良好,应满足内部材料单元密度梯度│x│尽可能小,尽量接近线性扩散;同时,为了保证结构边界清晰,应满足密度扩散沿着边界的切向进行,而避免沿着法向穿过边界扩散。因此,需选用合适的φ(│x│),根据上述要求,本文中选取φ(s) =s/(1+s2)。
2.2 优化数学模型
为了最大化结构的阻尼性能,考虑以结构的模态阻尼因子为目标对结构进行优化设计;同时为了考虑微结构中刚度相材料的连接性,基于非线性扩散法,将结构整体密度梯度的能量泛函加权至模型目标函数中,得到优化设计的数学模型:
findX(xi)
(11)
(12)
(13)
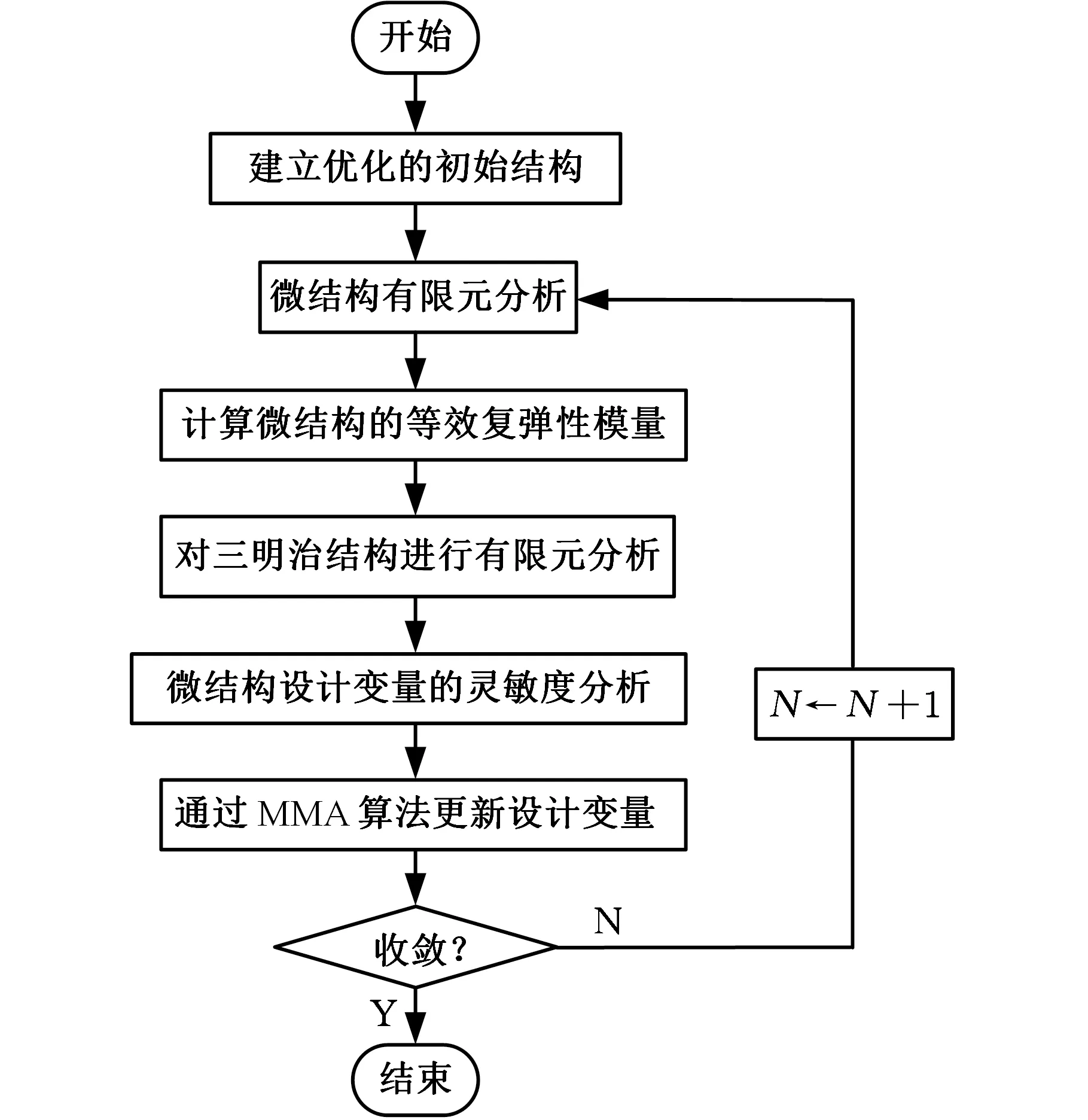
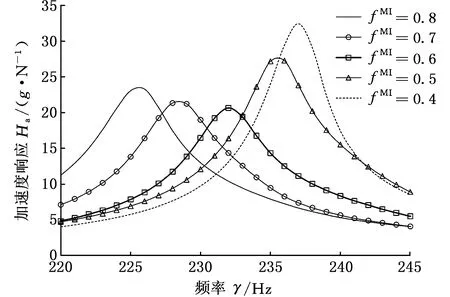
0 (14) 其中,X是设计变量,即复合阻尼材料微结构设计变量xi。式(12)为目标函数,第一项为结构阻尼目标函数,wk为第k阶模态阻尼比的权重,当kmin=kmax时, 仅对结构第k阶模态阻尼比进行优化,当kmin 在以结构宏观性能为目标的微结构设计模型中,对微结构单元的灵敏度分析要建立在对结构宏观性能分析的基础上。在宏观尺度上对结构进行有限元分析,计算出整体结构的性能,然后通过将宏观性能目标对微结构设计变量求导,即可得到微结构设计单元的灵敏度。阻尼复合材料微结构单胞的等效弹性矩阵DH为 (15) 式中,ui为微结构中第i个单元的位移场;│Y│为微结构单胞的体积;Y为微结构的设计域,Yi为单胞上第i个单元的体积;I为单位矩阵;b为应变位移矩阵;DMI为微结构上第i个单元的弹性矩阵。 为了获得清晰的设计结果,基于SIMP插值方法,微结构上第i个单元弹性矩阵的插值模型为 (16) 式中,p为惩罚系数,本文中p=3;D1和D2分别为刚度相材料和阻尼相材料的弹性矩阵。 根据式(15)和式(16),可得优化过程中复合阻尼材料的等效复弹性矩阵DH为 (17) 对于式(12)目标函数的灵敏度分析,可分别对两项进行求导再相加。第一项对设计变量灵敏度可通过式(6)对设计变量xi求导得到 (18) 其中,刚度矩阵Kv为 (19) 式中,B应变位移矩阵;n为结构阻尼层划分的单元数;Ω为单元体积。 通过式(19),可得式(18)中Kv的虚部和实部对设计变量xi的灵敏度分别为 (20) (21) 等效弹性矩阵对设计变量xi为 (22) (23) 将式(22)和式(23)分别代入式(20)和式(21),复合阻尼材料刚度矩阵虚部和实部对设计变量的灵敏度分别为 (24) (25) 将式(24)和式(25)代入式(18),可得到结构第k阶模态阻尼因子对微观结构设计变量的灵敏度。 目标函数第二项对设计变量的灵敏度为 (26) 当对设计域划分单元后,设xi在总体结构中的位置为图3所示的xa,b位置,则与其相邻的单元分别为xa-1,b、xa+1,b、xa,b-1、xa,b+1,如图3所示。根据散度的定义可得 图3 邻接单元示意图Fig.3 Adjacent element div(g(|xi|2)xi)=w1xa-1,b+w2xa+1,b+ (27) (28) (29) (30) (31) 将式(27)代入式(26)即可得到目标函数中第二项对设计变量的灵敏度。 考虑连接性的三明治阻尼复合结构拓扑优化设计方法的主要设计步骤如图4所示,包括如下几个设计步骤: 图4 优化设计流程Fig.4 Flowchart of the proposed topologyoptimization procedure (1)初始模型的建立。建立优化的几何模型,阻尼层设置为可设计域,其他为非设计域。 (2)微结构的有限元分析。对复合阻尼材料微结构进行网格划分,建立有限元模型,除四角点外所有单元设置为设计变量。通过式(17)计算单胞的等效复弹性矩阵DH。 (3)结构宏观性能有限元分析。使用步骤(2)得到的复合阻尼材料的等效复弹性矩阵DH计算整体结构的性能。 (4)灵敏度分析。使用式(18)和式(26)计算设计变量xi的灵敏度。 (5)使用移动渐近线法[15](method of moving asymptotes,MMA)更新设计变量。MMA方法是一种基于梯度的迭代寻优算法,通过引入移动渐近线,将隐式的优化问题转化成一系列显式的、可分离的、严格凸的近似子优化问题。每一步迭代中,通过用梯度类算法求解凸近似子问题来更新设计变量,适于处理目标函数复杂且具有多约束的拓扑优化问题。 (6)收敛判断。如果优化迭代的目标函数连续两次的差值小于收敛容差,或者迭代次数到达设定的最大值N,则退出循环,否则返回继续迭代,直到达到收敛条件。 为了验证所提设计方法的有效性,对两个不同边界条件的三明治阻尼复合结构进行拓扑优化设计,第一个为悬臂结构,第二个为两边固支结构。材料具体参数如表1所示。微结构优化中选取图5所示的构型,初始密度为微结构中体积分数设定值,四角点初始密度设置为0.001(铝合金),且迭代过程中保持不变,作为强制性连接约束。微结构划分为40×40个单元。 图5 初始微结构构型Fig.5 Initial guess microstructure 表1 材料属性 悬臂结构如图6所示,长1500 mm,总厚度为100 mm,上下表层厚度分别为25 mm,阻尼层厚度50mm。基板和阻尼材料参数如表1所示,结构左侧固定约束,构成悬臂板。 图6 悬臂结构Fig.6 A cantilever structure 为了研究阻尼材料在微结构中所占的体积分数对设计结果的影响,以结构前三阶模态阻尼比加权最大为目标,通过设置不同的体积约束条件对悬臂结构进行拓扑优化设计。图7所示为微结构不同阻尼材料体积分数约束下的设计结果,可以看出,不同体积分数下微结构的构型形态相似,都是“1”字形,随着体积分数的增大,阻尼材料的分布逐渐变宽,微结构等效弹性模量的实部和虚部都逐渐减小。表2所示为不同体积分数设计结果的模态频率和模态阻尼的对比,从表中可知,随着阻尼材料体积分数的增大,结构的频率逐渐减小,同时结构的阻尼逐渐增大,但是阻尼增大的幅度越来越小。图8所示为不同体积分数设计结果在第一阶模态频率处的频率响应对比,激励点和响应点都为悬臂结构右上角点。从图中频率响应曲线可得,结构的频率响应随着阻尼材料体积分数的增加先是逐渐减小,当fMI=0.6时达到最小值后,随体积分数的增大响应逐渐变大。由此可得,当微结构种阻尼材料的体积分数为0.6时结构的性能最优。 表2 不同体积分数设计结果性能对比 (a)fMI=0.4时设计结果 (b)fMI=0.5时设计结果 (c)fMI=0.7时设计结果 (d)fMI=0.8时设计结果图7 不同微结构体积分数设计结果Fig.7 Design results with different volume fractions 因为目标函数中加权了密度梯度的能量,所以设计问题已不再是纯粹的以阻尼比最大为目标的设计问题。文中以第k阶模态阻尼比为目标时并不会使设计结果的第k阶模态阻尼比是最优的,因此可认为设计结果性能的优劣对目标函数中模态阻尼比阶次的选取相关性较小。 图8 不同体积分数设计结果频率响应对比Fig.8 The simulated frequency response of thedifferent design result 为了进一步验证本文所提方法的有效性,对设计结果进行实验验证。考虑到成本以及测试精度,采用缩小的比例模型对三明治结构进行实验,长度和宽度方向缩放比例为1∶10,厚度方向为5 mm(易于粘贴加速度传感器的最小尺寸)。采用3D打印技术,分别打印阻尼材料体积分数为0.4、0.5、0.6、0.7和0.8的模型,打印后结构的尺寸为165 mm(长) ×6 mm(宽) ×10 mm (高),如图9所示。三明治阻尼复合结构的制造过程如下:首先通过3D打印技术打印出具有连接性的铝合金相结构,然后将环氧树脂填充于打印好的金属结构中,即可完成三明治阻尼复合结构的制造。 (a)三明治阻尼复合结构试件 (b)图a局部放大图(c)单胞示意图图9 制作的三明治阻尼复合结构试件Fig.9 The 3D printed sandwich composite structures 采用对比试验方法,在相同的实验条件下对不同的试件进行测试,以此来对比不同结构性能的优劣,图10为实验布置图,具体测试流程如下: (1)边界条件的施加。通过夹具将结构一端夹持来模拟悬臂结构。 (2)实验测试。通过锤击法对结构进行模态实验,锤击点如图10中箭头所指的点所示,拾取自由端响应。通过测试得到试件的模态频率和模态阻尼比,如表3所示。表3与表2的结果有所不同,主要原因在于对算例进行优化设计时使用的是平面应力单元,结构的厚度为1 mm,由于厚度较小,制作的试件很难粘贴传感器进行测试,因此在厚度方向上加大了结构尺寸;同时结构尺寸较大,不便于制作,采用模型实验对结构进行测试,尽管样件与仿真算例有所不同,但是实验都是在相同的条件下进行的,实验结果仍能够反映优化设计结果的性能。从表3中可知,随着阻尼材料体积分数的减小,结构的前三阶频率逐渐增大,结构的前三阶模态阻尼逐渐减小,这与表2所示的仿真结果趋势相同。试件在第一阶模态处的频率响应如图11所示,由图可知,随着微结构阻尼相体积分数的增大,结构的频率响应随微结构阻尼相体积分数呈现非线性变化,随着体积分数增大,结构在第一阶模态处的频率响应依次为32.42g/N、29.40g/N、20.64g/N、21.22g/N、23.27g/N,结构响应首先逐渐减小,当体积分数为0.6时响应值最小,随后随着体积分数的增大,结构的响应逐渐增大。这主要是因为结构的频率响应与结构的刚度和阻尼同时相关,以牺牲结构刚度为代价获得更大的阻尼并不能有效减小结构的响应。对于复合结构而言,存在一个最优的刚度和阻尼使得结构的响应最小。 图10 实验布置图Fig.10 Experimental setup 表3 不同试件实验测试结果 图11 实验测试频响函数Fig.11 The experimental frequency response of thedifferent design result (1)本文提出了一种考虑连接性的三明治阻尼复合结构拓扑优化设计方法,通过组合强制性连接约束和非线性扩散法,实现了对阻尼复合结构的连接性设计,并结合3D打印技术实现了三明治阻尼复合结构的材料-结构-设计-制造协同优化。优化后的结构阻尼变大,结构的频率响应变小。 (2)在考虑微结构连接性时,因在阻尼目标函数中加权了密度梯度的泛函,所以不同阻尼比目标函数下得到的设计结果的性能差异较小,目标函数的选择对设计结果的影响很小。 不同体积分数的仿真和实验结果表明,在微结构上存在最优的阻尼材料体积分数使优化后的结构频率响应最小。2.3 灵敏度分析


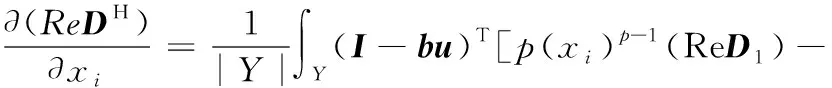




2.4 优化设计流程
3 数值算例









4 实验验证



5 结论

