水驱砂岩油藏在不同水质下的渗透率时变特征
王建忠,宋宪坤,付颖超,孙莲婷,徐进杰
[中国石油大学(华东) 石油工程学院,山东 青岛 266580]
砂岩作为多孔介质是一种天然的过滤材料。在1856年,法国工程师达西利用填满砂子的管柱过滤城市用水发现了著名的达西定律。根据石油行业油田水质标准(SY/T 5329—2012),将油田注入水分为5个水质等级,不同水质的注入水因污染物种类、含量和粒径的不同,对地层的堵塞规律、伤害程度以及水驱开发效果的影响也不尽相同。这种伤害不是因为“五敏”,也不是“压敏”,而是因为水质问题引起的,本文将这种原因称之为渗透率水质敏感性。近些年,国内学者们的最新研究阐明了水质对提高注水开发效果的重要性[1-2]。李明忠等给出了注入水中各污染物引起表皮系数变化的具体计算方法[3];Wojtanowicz A K、张光明和李军等不少学者围绕着注入水中污染物含量对地层渗透率的伤害规律做了大量研究[4-11];Rochon J,Basan P B和Zhang N S等学者建立了简单分析方程,预测注入水中悬浮固体对地层伤害以及影响水驱开发效果的程度[12-16]。Amanat Ali Bhatti等综合利用水动力学及电测法对储层渗透率进行预测[17],Xia Dongling从沉积、成岩的角度,提出了表征储层渗透率的方法[18]。学者们的研究意在阐明水质对注水开发效果的影响,但是对水质造成储层渗透率伤害的规律缺乏定量描述,这在一定程度上制约着油田长期注水的水质决策。在前人研究的基础上,本文给出注入水对地层渗透率的伤害规律的数学描述和理论推导,在一定程度上为油田长期注水的水质决策提供指导。
1 注水对砂岩油藏渗透率的伤害
油田注水过程中,常见的引起注水系统堵塞的主要因素如表1所示。实际上,地层中的孔喉对注入水中的污染物起到了一个过滤作用,我们把它称为砂岩的过滤效应。注水开发油田进入高含水开发期后,优势通道的形成是不可避免的问题。油田经过长期注水开发,大部分井区己进入高含水期,大量注入水沿注采优势通道突进,造成许多区块注入水低效甚至无效循环,大大降低了油田开发效果和经济效益。优势通道的形成造成了地层平均渗透率变大的假象,而实际含油区附近的地层却已被注入水中的污染物堵塞。因此需在对识别出的优势通道采取有针对性的封堵措施后,结合注水水质标准,选择合适的注入水,提高水驱开发效果。
对于高含水期砂岩油藏,特别是长期注入水质不达标的水,会造成地层孔隙被堵塞,严重伤害地层渗透率。一方面,注入水中的污染物会在井壁或注水层端面形成滤饼;另一方面,水中的污染物会在地层孔隙内沉淀或被吸附导致孔隙变小,注入水流速越大,污染物会就会进入离注水井更远的地层。洗井只能解决井筒表层的堵塞问题;酸化以及压裂方式只能解决井筒附近地层的堵塞问题,而且酸化或压裂后,注水会堵塞离井更远的地层。
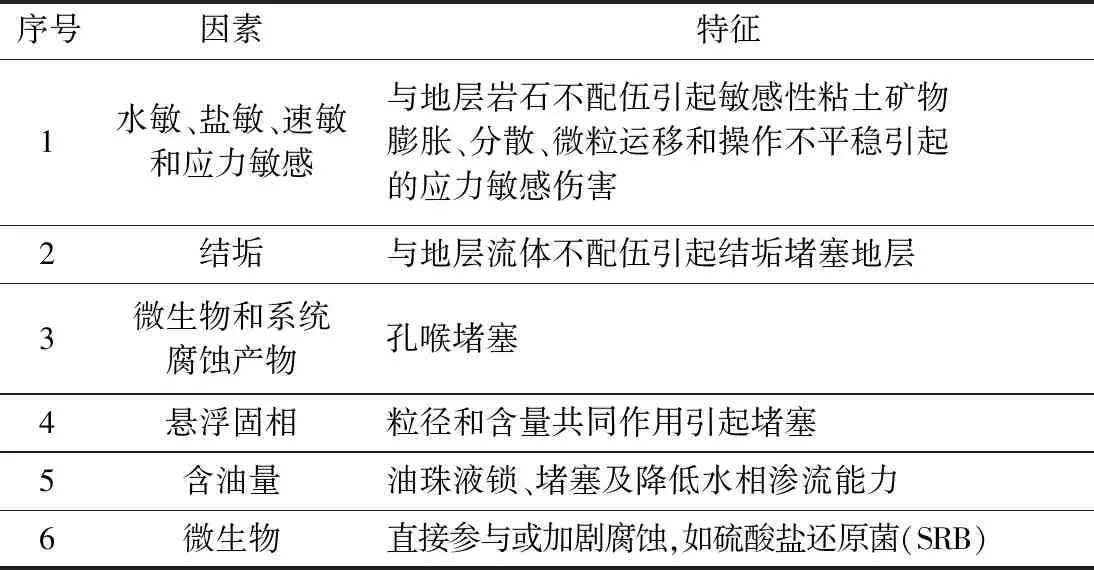
表1 引起注水系统堵塞的主要因素Table 1 Main factors causing blockage in water injection systems
2 渗透率衰减规律及表征方法
因为受不同注入水水质的长期影响,地层渗透率逐渐下降,本文把这种现象定义为地层渗透率的水质敏感性。在注入水水质标准基础上,为深入研究地层渗透率的水质敏感性,按照注入水水质标准中5种注入层平均空气渗透率从小到大的顺序,把对应不同控制指标下的不同注入水水质依次命名为Ⅰ级水质、Ⅱ级水质、Ⅲ级水质、Ⅳ级水质和Ⅴ级水质(表2)。在表2中,仅列出了两项主要影响水驱开发效果的水质控制指标,即悬浮固体含量与含油量。
根据理论研究结果和实验室的实际条件,通过对大量岩心进行室内地层伤害实验,研究5种注入水水质对不同地层渗透率注入能力的影响,得到不同地层渗透率在不同水质下的注入能力差异,即地层渗透率下降情况。进一步分析在确定注入水水质的情况下,不同地层渗透率随无因次注入量增加而衰减的现象。实验条件如下。
1) 实验温度为70 ℃。
2) 实验水样为注入水水质标准下以悬浮物含量及含油量为主要控制指标配置的5种水样。
3) 储层物性以渗透率为主,标准岩心渗透率划分标准为:(1 500~2 000)×10-3,(500~1 500)×10-3,(50~500)×10-3,(10~50)×10-3和(1~10)×10-3μm2,在实验过程中需在不同岩心渗透率范围内挑选大量的岩心进行实验。
4) 实验中所用岩心有天然岩心和人造岩心,人造岩心胶结程度较好,无水敏性。实验前经溶剂驱替、蒸馏水高速冲刷,避免了加工中引入的微粒物质对实验结果的影响。天然岩心取自目标油区。
5) 鉴于水质变化相对较快,实验过程中采用图1所示的并联实验方案。
实验流程如下。
1) 将岩样洗油、风干、烘干后,测空气渗透率,饱和地层水后测孔隙度。

表2 SY/T 5329—2012 注入水水质标准Table 2 SY/T 5329-2012 recommended standard for injection water quality

图1 水质影响研究实验平台Fig.1 Experimental platform for water quality impact assessment
2) 借助地层伤害实验设备,通过恒温箱模拟地层温度70 ℃,配置Ⅰ级水质,将饱和好地层水的岩心置于岩心流动装置中,将围压缓慢加至2.0 MPa。实验过程中始终保持围压大于上游压力1.5~2.0 MPa,以此消除围压对实验结果的影响。
3) 在恒定流速下,让注入水大量的流过岩心,测定其渗透率随流量增加的变化情况。控制注入水流速在临界流速以下,并计算无因次注入量,在无因次注入量分别为5,10,20,50,100,150 和200 孔隙体积倍数(PV)时测量各岩心的渗透率,此时的渗透率K与岩心初始时的渗透率K0之比就是渗透率保留率。
其余4类水质依次用这种方法测量无因次注入量和渗透率保留率的对应数值,以此来研究渗透率保留率随无因次注入量的变化规律,进而从定量的角度分析水质对储层渗流物性的影响。
以Ⅰ级注入水水质条件下,渗透率为213.91 × 10-3μm2的岩心为例,根据表3中盖岩心渗透率保留率的变化数据,经指数拟合后如图2所示。
上图可以看到相关性系数接近1,初步认为岩心渗透率保留率(K/K0)与无因次注入量(Qi)之间具有指数关系。在此基础上对所有实验数据指数拟合,如图3所示,相关性系数均接近1,可看出在Ⅰ级水质下岩心渗透率保留率K/K0与无因次注入量Qi呈较好的指数关系。
其余4类水质依次用这种方法测量无因次注入量和渗透率保留率,并对所有实验数据进行指数拟合。拟合结果如图4至图7所示,相关性系数同样均接近1,均呈较好的指数关系。
随无因次注入量增加,岩心渗透率不断降低,低渗岩心比高渗岩心变化更加显著。从开发角度考虑,因5种注入水水质的悬浮固体含量与含油量不同,故实验岩心渗透率降低是悬浮固体含量与含油量共同作用的结果。同一种注入水水质对不同岩心渗透率区间的伤害程度不同,5种水质对同一岩心渗透率区间的伤害程度也不同,可看出地层渗透率衰减程度与地层综合物性、注入水中悬浮固体含量与含油量有关。
在确定注入水水质情况下,随着累积注入孔隙体积倍数的增加,岩心渗透率不断衰减,衰减速度逐渐减慢。对注水开发的油田来说,只要注水就会增加无因次注入量,注入水中的污染物会堵塞岩心,导致岩心渗透率大幅下降。
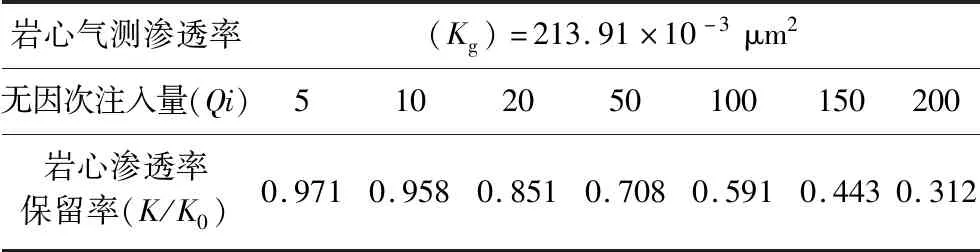
表3 Ⅰ级注入水水质条件下岩心渗透率保留率变化数据Table 3 Permeability retention rate under Class Ⅰ injection water quality
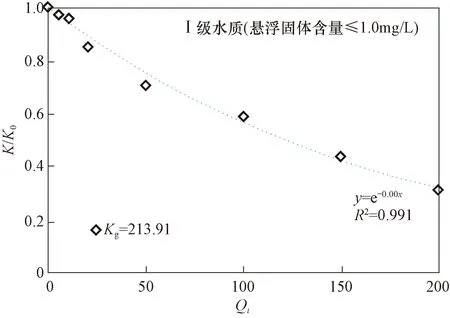
图2 Ⅰ级注入水水质条件下岩心渗透率保留率变化拟合曲线Fig.2 Fitting curve of permeability retention rate under Class I injection water quality
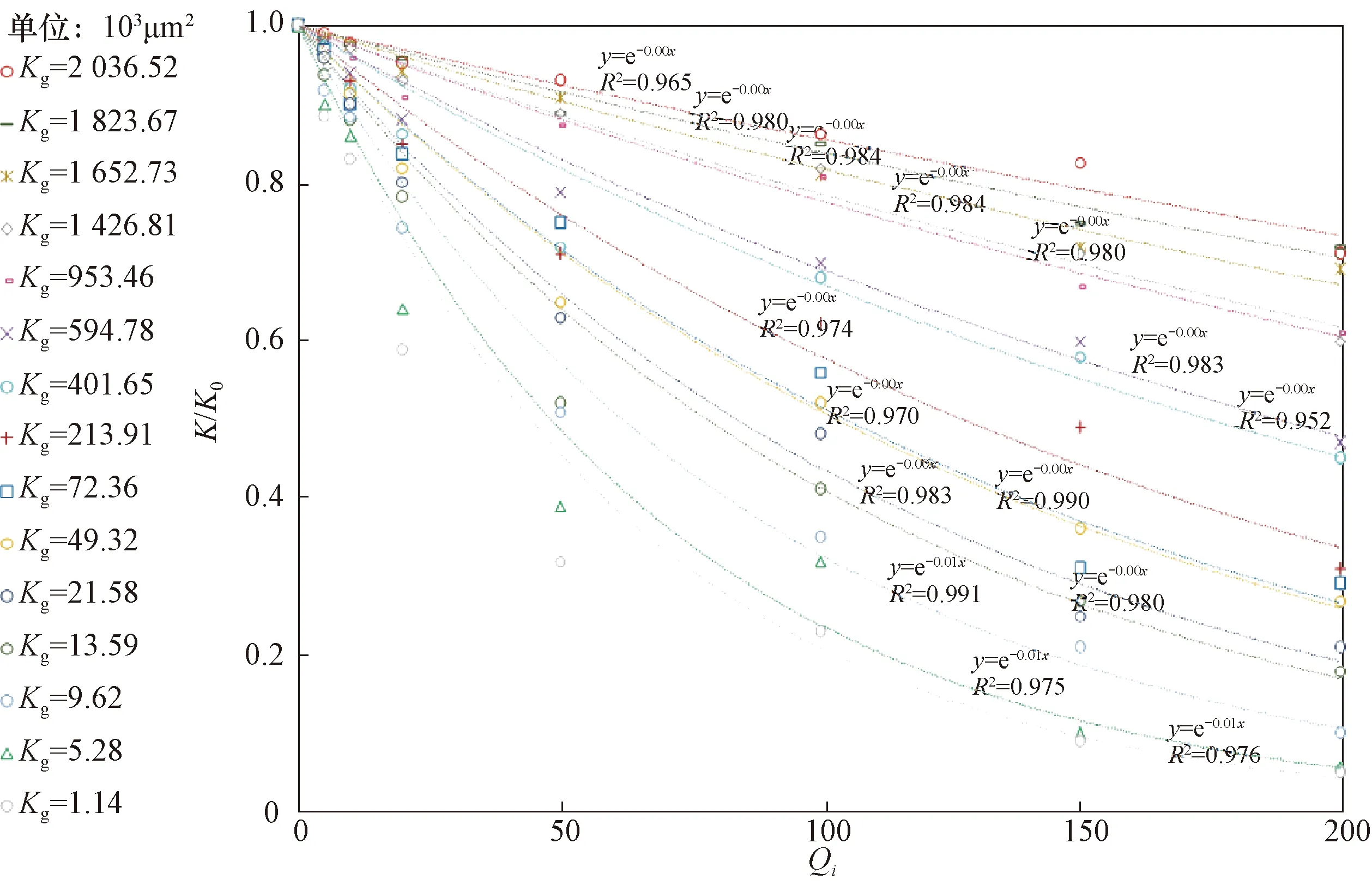
图3 在Ⅰ级注入水水质条件下不同岩心渗透率保留率随无因次注入量变化关系拟合曲线Fig.3 Fitting curves of permeability retention rates changing with dimensionless injection rates for different cores under Class I injection water quality
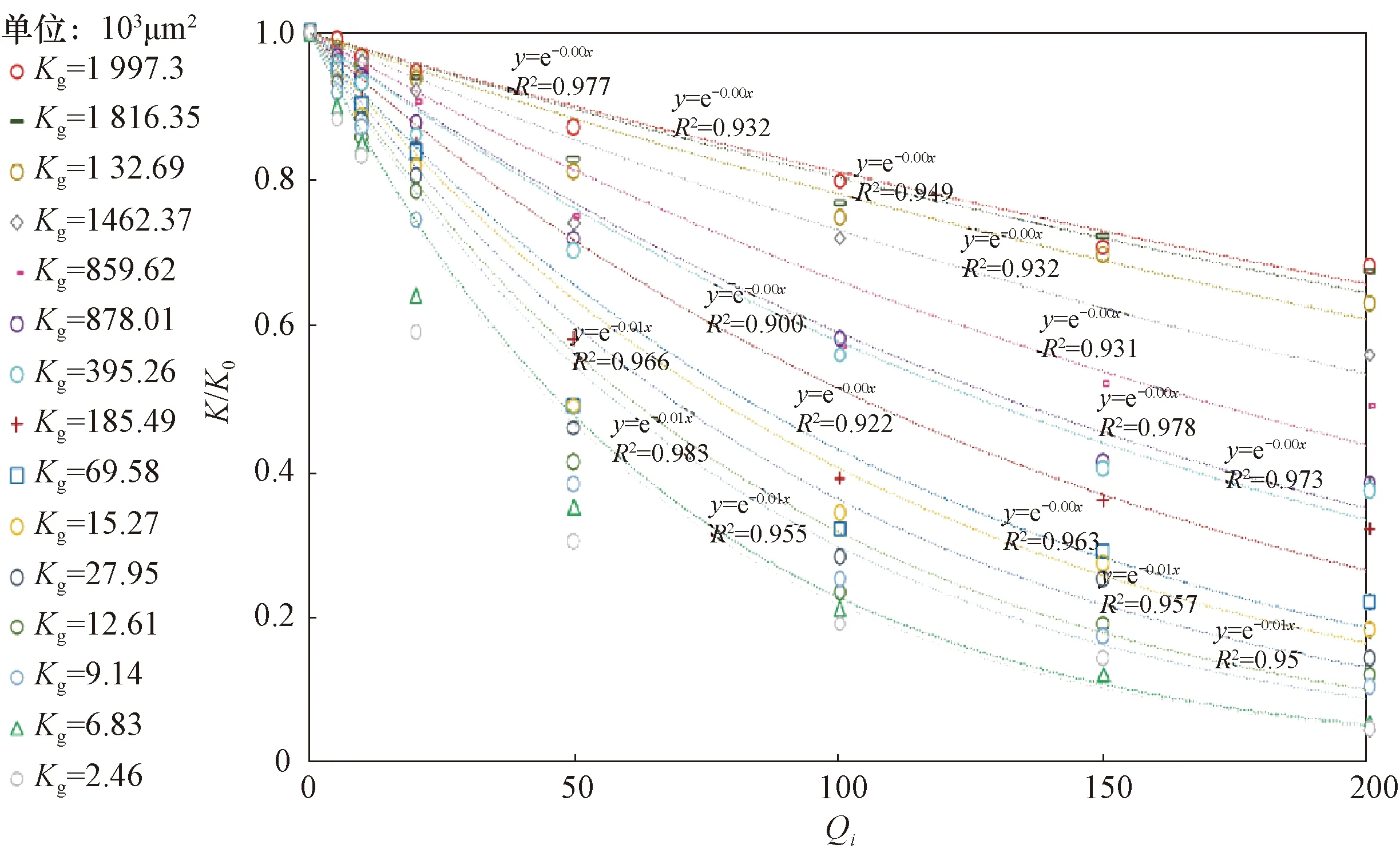
图4 在Ⅱ级注入水水质条件下不同岩心渗透率保留率随无因次注入量变化关系拟合曲线Fig.4 Fitting curves of permeability retention rate changing with dimensionless injection rate for different cores under Class Ⅱ injection water quality
3 渗透率水质敏感性
将图3中各拟合公式指数中无因次注入量的倍数用θ表示,归纳得到规律公式如下:
K/K0=e-θQi
(1)
式中,θ为地层渗透率的水质敏感系数,其物理意义是在确定注水水质下,注入层单位渗透率随无因次注入量的变化速率,10-3;K为当前地层渗透率,10-3μm2;K0为水驱开发前地层渗透率,10-3μm2;Qi为无因次注入量,即注入水的孔隙体积倍数。
根据θ的定义,可用如下公式表示:
(2)
对公式(1)分离变量积分可得:
lnK=-θQi
(3)
在水驱开发前,即Qi=Qi0=0时,K=K0,则有:
lnK0=-θQi0
(4)
由公式(3)与公式(4)相减变形可得:
K/K0=e-θQi
(5)
经理论推导得到的公式(5)与大量实验数据拟合出的规律公式一致,说明理论充分验证了实验规律的正确性。将公式(5)变形可得:
K=K0e-θQi
(6)
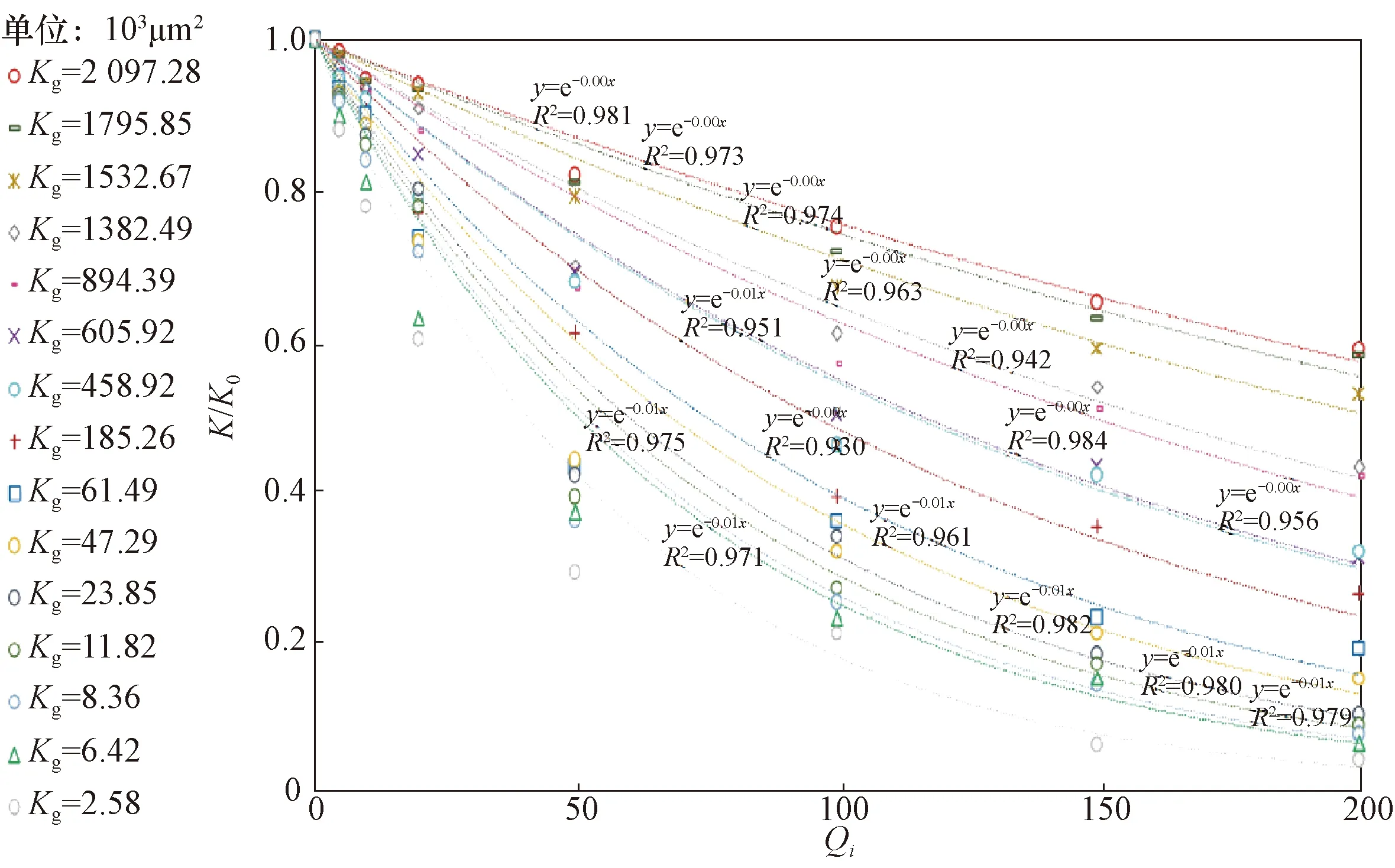
图5 在Ⅲ级注入水水质条件下不同岩心渗透率保留率随无因次注入量变化关系拟合曲线Fig.5 Fitting curves of permeability retention rate changing with dimensionless injection rates for different cores under Class Ⅲ injection water quality

图6 在Ⅳ级注入水水质条件下不同岩心渗透率保留率随无因次注入量变化关系拟合曲线Fig.6 Fitting curves of permeability retention rate changing with dimensionless injection rates for different cores under Class Ⅳ injection water quality
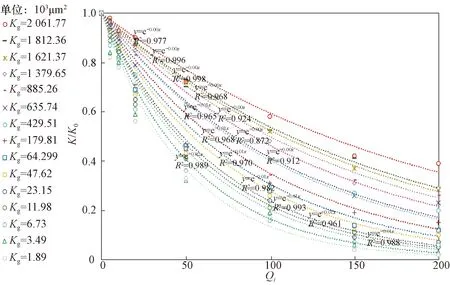
图7 在Ⅴ级注入水水质条件下不同岩心渗透率保留率随无因次注入量变化关系拟合曲线Fig.7 Fitting curves of permeability retention rate changing with dimensionless injection rate for different cores under Class V injection water quality
通过公式(6),可定量计算或预测在确定注入水水质条件下,目的地层经历一定注水历史后,其渗透率的变化规律。由上可看出,高含水期老油田,当前地层渗透率相比水驱开发前地层渗透率发生了巨大变化。为使公式(6)中θ取值更加精确并且便于计算,将实验数据重新整理,分别在(1 500~2 000)×10-3,(500~1 500)×10-3,(50~500)×10-3,(10~50)×10-3和(1~10)×10-3μm2的渗透率范围内,通过最小二乘法依次做出在5种不同水质条件下,取负对数的岩心渗透率保留率随无因次注入量变化的多条拟合直线。以渗透率为(1 500~2 000)×10-3μm2的岩心为例,图中直线的斜率即为θ值。通过最小二乘法做出在5种不同水质下,渗透率的水质敏感系数的大小随渗透率变化的多条拟合直线,并得到对应拟合直线的方程(图8)。通过对全部实验数据进行归纳,经线性插值与扩展,得到介于(1~2 000)×10-3μm2的渗透率所对应的θ值(表4)。
在确定的注入水水质和储层渗透率下,根据表4做线性插值,可得目前储层的水质敏感系数θ,将θ值带入公式(6),便计算出一定注水历史后的储层渗透率,为决策注水水质提供参数依据。
将表4中Ⅰ—Ⅴ级水质各渗透率对应的水质敏感系数θ,与现行的注水水质指标(表2)中各渗透率范围相对应,将范围下的水质敏感系数定义为水质准数θ′,其物理意义为在确定的注水水质和渗透率下,适合注入目标油层的最大界限θ值。经过计算出的值小于其相应的水质准数时,表明当前使用的水质与地层是匹配的,不需要考虑水质选择问题。当计算出的值大于θ′时,则说明目前正在使用的水质已经与当前储层不匹配,这个时候就需要根据对应的θ′,进行水质的重新选取。
4 考虑注水历史的水质决策方法
在目标区块注水过程中,以单井作为计算单位,进行水质决策方法的研究。在计算地层的水质敏感系数θ时,需明确单井储层渗透率及当前所用水质。计算水质敏感系数之后,与相应的水质准数进行对比,用以判断现在所用的水质能否适应当前储层。
计算出的水质敏感系数小于相应的水质准数,则说明目前注入水水质符合水质标准。相对来看,如果大于的话,就需要考虑水质决策,具体注水水质决策的步骤如下。
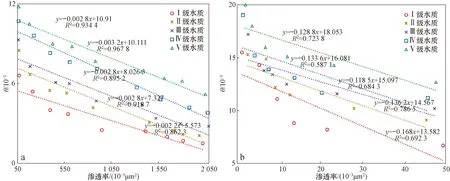
图8 五种水质下水质敏感系数(θ)的大小随渗透率变化拟合直线Fig.8 Fitting results of water quality-sensitivity coefficient changing with permeability under five types of injection water qualitya.渗透率>50× 10-3 μm2;b.渗透率<50× 10-3 μm2

表4 渗透率水质敏感系数(θ)取值Table 4 Water quality sensitivity coefficients of different permeability
1) 计算单井对应油层孔隙体积,如公式(7)所示。
φφi=Shφ
(7)
式中:V为单井储层孔隙体积,m3;S为单井所控油层的供油面积,m2;h为油层有效厚度,m;φ为储层平均有效孔隙度,%;i为注水井标号,i= 1,2,3,…,N。
2) 计算单井的无因次注入量,如公式(8)所示。
Qi=Qti/Vφi
(8)
式中:Qi为单井的无因次注入量,无量纲;Qti为单井从开始注水到目前累积总注水量,m3;Vφi为单井对应油层孔隙体积,m3。
(9)
考虑经济因素的限制,为防止出现某一口井的水质不匹配,就更换整个注水系统水质的做法,当所控储层的θ值大于对应的水质敏感系数θ′的井的数量大于整个注水系统所有井数量的1/2,此时再根据该水质决策方法重新选择水质。
4) 计算当前整个目标区块对应油层的平均渗透率。因不同井注水量不同,对储层渗透率伤害程度不同,所以需要在取得各单井的月度注入情况报表的基础上,依靠其中数据,统计目前各注水单井的实际注入量Qi,再通过公式(10)计算出该注水系统对应储层的平均渗透率,再根据注水水质标准决定注水系统目前应该匹配哪种水质。
(10)
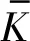
5) 在注水系统所对储层的平均渗透率确定的情况下,结合注水水质标准,选择目前注水系统适合的注水水质。
5 油田应用模拟
以孤东油田为例,该油田目前单元开发出现含水高、液量低与压力高的特点。利用所建立的七区西单井注采模型,定压差生产,压差为2 MPa,进行产能预测,用以重新审视水质决策。模拟水驱前的地层平均渗透率约为2 000×10-3μm2,研究注入不同水质下的储层渗透率及产能变化情况,为水质决策方法提供论证。
综上所述,注入不同级别的注入水对储层渗透率的改变情况不同。从衰减情况看,当注水达到20 a左右时,Ⅴ级水质下的储层渗透率呈现明显的下降;在注水达到50余年后,渗透率下降速度开始逐渐变慢,最终下降至580×10-3μm2左右。水驱的过程中如果堵塞达到了一定的程度,注入水中的污染物很难继续进入储层,造成渗透率下降变缓的情况,甚至有些情况下会发生“憋缝”,出现储层渗透率增大的假象。
注水40 a后,通过线性差值可得θ值为0.005 31,当前累积注水量38 ×106m3,计算当前单井储层孔隙体积为306×103m3,当前单井无因次注入量为124 PV,当前渗透率为1 034.687×10-3μm2,水质准数θ′为0.006 8,因此需要进行更换水质的重新决策。依靠行业注水标准表1可知当前应选用Ⅳ级水质进行生产。通过图9可以看出,当注水达到40年左右,从Ⅴ级水质换到Ⅳ级水质后,继续进行注水,产量相应增加。如图10所示,累积产油量增加了约2.5×104m3,采收率提高了1.3%。然而若继续更换较好的水质,产能虽然得到提高,但效果接近Ⅳ级水质,这时候考虑到经济因素,选择Ⅳ级水质最为合适。
6 结论
1) 水质一定下,岩心的K越高,K/K0下降越慢;K越低,K/K0下降越快。对于高渗岩心,水质的影响比较大,当无因次注入量在200 PV时,Ⅰ级水质中高渗岩心渗透率保留率会在0.7左右,而在Ⅴ级水质中则是处于0.3左右。对于渗透率略低的岩心,水质因素的影响较小,K/K0会快速下降到一个较低的水平。
2)K/K0与无因次注入量Qi的关系公式,可用于重新审视水质与地层渗透率的匹配关系,进而定量计算和预测一定注入历史下具体注水层的渗透率。
图9 渗透率为2 000× 10-3 μm2的储层在不同水质条件下渗透率与产量的变化情况Fig.9 Change of permeability and production with time for reservoirs with a permeability of 2 000×10-3 μm2 under different injection water qualitya.渗透率变化情况;b.产量变化情况
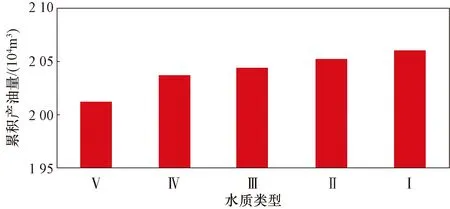
图10 五种不同级别水质条件下累积产油量对比Fig.10 Comparison of cumulative oil production from reservoirs flooded with water of different quality
3)在定量表征数学模型基础上,定义地层渗透率的水质敏感系数θ,确定了注水决策界限为11.9~13.4,7.2~13.2,6.6~9.2,5.3~8.5和5.3~6.7。以此作为与储层相适应的水质选取标准,为水质决策提供了参数依据,通过水量加权确定储层平均渗透率,形成水质决策方法。

