海浪流场作用下的邮轮实船运动仿真

周新聪，肖仲歧，张 聪，欧阳武，黄 健

(1. 武汉理工大学 能源与动力工程学院，湖北 武汉 430063；2. 船舶动力工程技术交通行业重点实验室，湖北 武汉 430063；3. 国家水运安全工程技术研究中心可靠性与新能源研究所，湖北 武汉 430063)

0 引 言

大型豪华邮轮作为一种拥有高附加值、高技术要求以及高难度的船舶，一直被誉为“海上流动五星级宾馆”，对于中国船舶行业来说这也是一块未经开发的空白领域。大型豪华邮轮的建造意味着我国在相关领域上的重大突破，而随着国际海事组织对于能效日益严格的要求以及邮轮本身对于经济性以及舒适性的追求，有必要追求最佳的能效表现。因此，有必要研究船舶在真实海况下航行的运动性能。

Zhao等[1]建立了评估船舶在真实海况下航行能效的综合化船舶推进模型。Yang等[2]对LNG船进行了考虑液舱晃荡与船体耦合的迎浪和斜浪中的数值模拟。廖炜昊[3]利用简化模型对波浪增阻与推进主机功率变化关系进行了研究。本文针对某大型邮轮基于粘性流的CFD理论建立了数值波浪水池，对邮轮在基于JONSWAP海浪谱的不规则波浪中航行进行流体仿真，模拟了一定的海况下船体所受阻力变化以及运动响应，通过对计算结果的对比为邮轮能效的提高提供一定依据。

1 数值模拟

1.1 控制方程

本文采用商用仿真软件STAR-CCM+对数值波浪水池中流场及船舶运动进行仿真，其流体运动依托于RANS的k-ε湍流模型，船体在三维数值波浪水池中的运动响应属于不可压缩多相流流动同时不涉及热量的传递，只需考虑质量以及动量的守恒，故其基本控制方程组如下：

质量守恒

动量方程

其中：ρ为密度，即单位体积的质量；v为连续体速度；⊗表示克罗内克乘积；fb为作用于连续体的单位体积的各种体积力（例如重力和离心力）的合力；p为压力；T为粘性应力张量，I为单位张量，－∇·(pI)+∇·T=∇σ ，σ=－pI+T意为应力张量为法向应力与剪切应力之和。

自由液面追踪采用VOF法，该方法假设网格大小足以求解各相之间的交界面位置及形状。通过对每个网格单元中各相的体积分数αi来描述交界面相的分布与位置，当 αi=0 时代表该网格单元中不存在相i；αi=1 时代表该网格单元完全由相i填充；而0＜αi＜1时代表该网格处于相的交界面上。

1.2 边界造波与消波

为了尽可能模拟真实海况，本文选用基于JONSWAP海浪谱生成的不规则波，同时随机数发生器将使用固定种子以提供相同的波形图案从而方便对比。

其频谱表示为[4]：

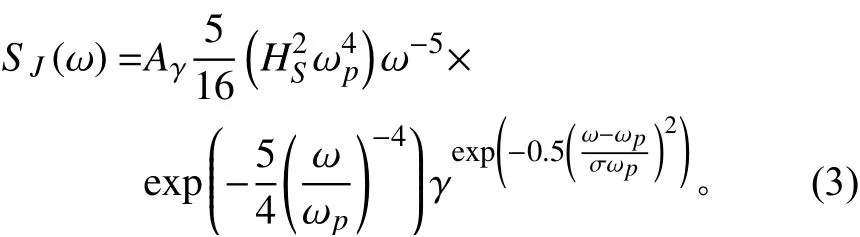
其中： γ=3.3， 属于无量纲峰形参数；Aγ=1－0.287 ln(γ) ，为归一化因子；σ为频谱宽度参数，小于或等于谱峰频率ωp时 ，取 σa=0.07，大于谱峰频率时，取σb=0.09。

为了避免VOF波在边界发生反射对计算结果产生干扰，于出口及计算域侧面设置具有波阻尼的消波区，其阻力方程为[5]：

其中，xsd为波阻尼区域在x方向上的起点；xed为其在x方向上的终点，即边界；f1，f2和nd为阻尼模型的控制参数；w为垂直方向上的速度分量。

1.3 六自由度刚体运动

在动态流体相互作用(DFBI)分析中，流体区域与六自由度刚体耦合，根据作用力计算六自由度刚体的运动。然后，流体网格严格按照计算得出的刚体运动进行移动。在求解中具有2个坐标系，即基于全局的惯性坐标系以及以船体质心为原点的局部坐标系。

由于求解对象为迎浪航行的船舶，其运动包括沿z轴方向的平移及以y轴为轴线的旋转，即升沉与纵倾，故其运动方程包括平移及旋转。其平移方程依据全局惯性坐标系建立：

其中：m为体质量；v为 平移速度；f为船体所受合力。

其体旋转方程依托于以船体质心为原点的局部坐标系：

其中：M为惯性矩张量；ω为刚体角速度；n为船体所受合力矩。

2 仿真模型

本文以某大型邮轮为计算对象，其相关参数见表1。

表1 目标邮轮船体相关参数Tab. 1 Relevant parameters of target cruise ship

建立实尺度模型后，其具体外形如图1所示。

图1 船体模型Fig. 1 Hull model

根据模型尺度划分计算域，由于实尺度模型较大，考虑船体的对称性，计算域取船舶左侧一半，不规则波的最大波长 λmax=60·H1/3，H1/3为有义波高，其宽度及水深约为2倍最大波长，水面以上部分高度约为1倍最大波长，水池前段既其波浪水流入口处位于船首部上游约2倍最大波长处，而尾端也即水池出口位于船尾部4倍最大波长处，见图2。

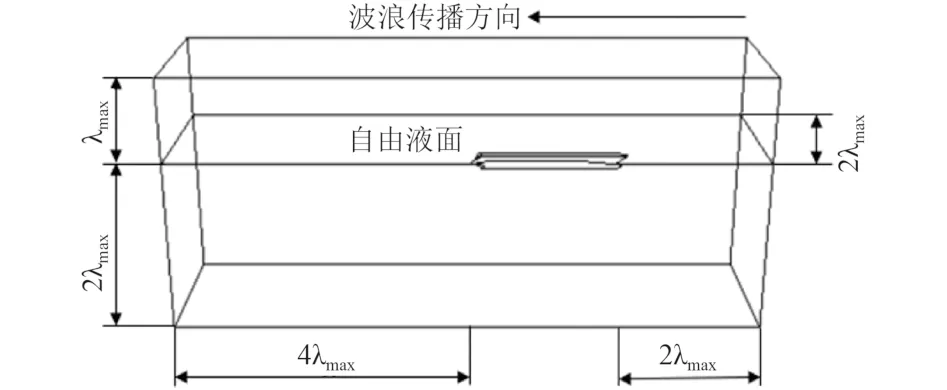
图2 计算域划分Fig. 2 Division of computing domain

网格划分时针对船体周围水域及自由水面进行局部加密，根据文献[6]中对于网格收敛性的论证，对以自由液面为中心，上下1.5倍H1/3范围内的网格加密，其中X和Y方向上的网格尺寸不得超出 λ/n1，Z方向上尺寸约为H1/3/n2，时间步长小于Tp/2.4·n1，其中H1/3为有义波高，λ 为波长，n1=80～100,n2=20，Tp为谱峰周期。为了在精度与计算时间之间取得平衡，对于远离自由液面及船体表面的区域过渡至较粗的网格，最终网格划分结果如图3所示。

图3 局部加密网格划分Fig. 3 Local mesh refinement

不同于船舶缩比模型尺度下的仿真，为确保模拟结果的准确性，船体壁面第一层网格厚度应使壁面Y+值大体保持在30～300之间，实船尺度下由于雷诺数的增加，壁面Y+值往往会大于300，此时船体Y+值除少数位置外应该保持不大于10 000[7]，同时为确保模拟精度，设定实船平均沙粒粗糙度hs为0.03 mm。

在此基础上，对网格尺寸对精度的影响进行研究，划分了3套网格，其基础尺寸分别为 Sbasic， 1.225Sbasic以及1 .5Sbasic。以工况6为目标，计算结果与《港口工程荷载规范》提供的公式计算[8]所得理论结果对比，如表2所示。

表2 网格收敛性分析Tab. 2 Analysis of grid convergence

可以看出，随着网格的加密，其计算精度逐渐上升，而当其基础尺寸为 Sbasic时，误差已足够小，同时若再加密网格，网格数大于1 100万，其计算时间将进一步拉长，故最终选定的网格尺寸其划分的网格总数为1 150万左右，在这个基础上时间步长度向下取整，最终长度为0.04 s。此时，船体表面Y+值分布如图4所示。

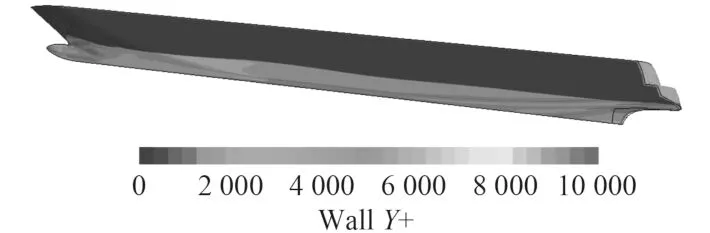
图4 船体表面Y+值分布Fig. 4 Distribution of Y + value on hull surface

3 计算结果

数值模拟时通过动态流体相互作用（DFBI）分析其运动响应，模型释放时间为1 s，缓冲时间为10 s，入口处持续生成波浪，同时计算时间步长取0.04 s，工况见表3。以邮轮在海流流速为1.3 m/s，有义波高为2.8 m且谱峰周期为10 s的海况下航行的仿真结果为例，计算结果如图5和图6所示。

表3 工况列表Tab. 3 List of working conditions

图5 运动响应时历变化曲线Fig. 5 Time series curve of motion response

图6 剪切及压差阻力时历变化曲线Fig. 6 Time series curve of shear and differential pressure resistance

由图5和图6可知，当该船在海浪水面顶浪航行时，阻力随运动响应发生变化，其中剪切阻力基本维持稳定，压差阻力根据船舶运动响应状态变化。最终通过模拟得到邮轮船身在不同海况下顶浪逆流时的流场示意如图7所示，阻力平均值R、纵倾均值θ以及升沉均值h如表4所示。

图7 船舶顶浪航行兴波Fig. 7 Making waves by sailing on top of waves

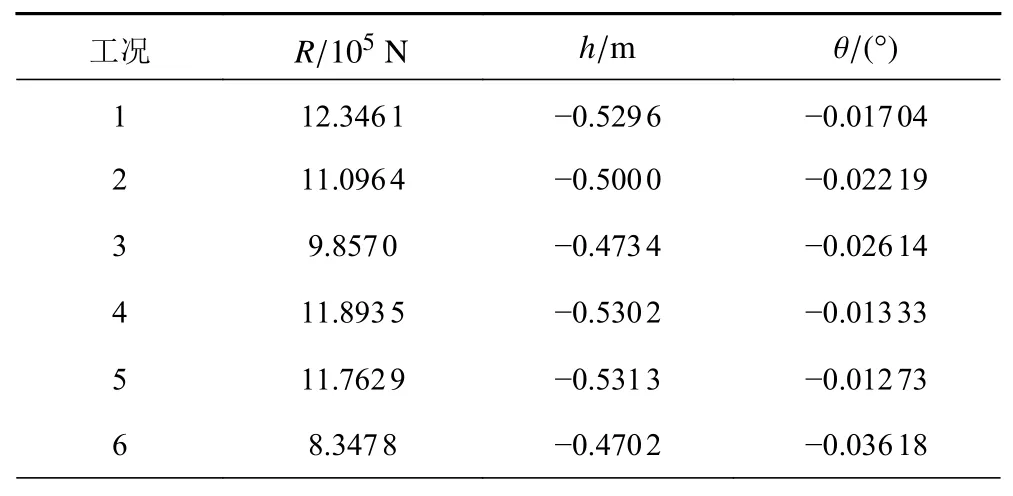
表4 仿真计算结果Tab. 4 simulation results

4 结果对比分析

4.1 海流流速影响

对比海流流速不同的3个工况，其阻力以及根据静水工况修正后的运动响应时历曲线如图8～图10所示。

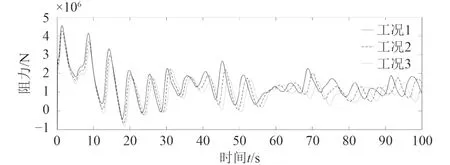
图8 工况1～工况3阻力时历对比Fig. 8 Comparison of resistance time histories of working conditions 1, 2 and 3

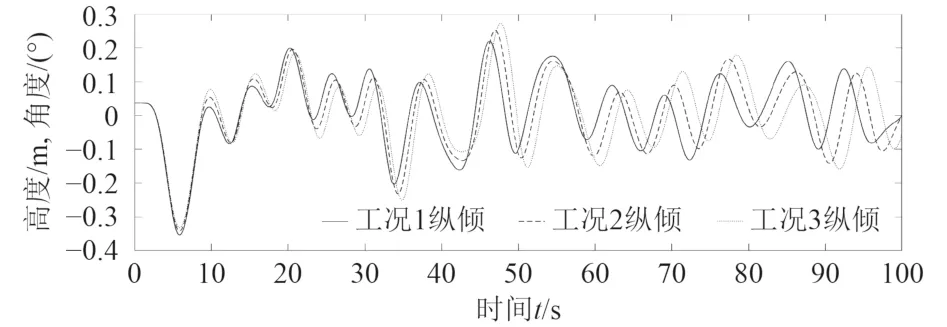
图9 工况1～工况3纵倾时历对比Fig. 9 Comparison of trim time histories of working conditions 1, 2 and 3

图10 工况1～工况3升沉时历对比Fig. 10 Comparison of heave time histories of working conditions 1, 2 and 3

通过分析可得，随着海流流速的减小，其最开始阻力及运动响应的变化趋势基本不变，然而在经过一段时间之后，流速较慢的工况在时历变化上开始出现明显的滞后，且滞后随着时间的推移越来越大。具体原因可能为海流流速直接影响到了船体遇浪的相对速度，使其在遭遇海浪的频率上出现了变化。对船体稳定之后的运动响应曲线进行分布估计，如图11所示。

图11 运动响应幅值分布估计Fig. 11 Estimation of amplitude distribution of motion response

由图11可知，当海流流速发生变化时，邮轮的纵倾运动只在平衡位置附近发生一定的变化，而其升沉运动随着海流变慢，越来越倾向于减小吃水，同时也更易偏离平衡位置。

4.2 海浪周期影响

对于海浪谱峰周期变化的工况1、工况4、工况5，其阻力及修正后的运动响应曲线对比以及分布估计如图12所示。在其他条件不变的情况下，随着谱峰周期的变短，其波长随之变短，此时其阻力及运动响应总体趋势不发生变化，但其上下波动的范围随着海浪周期的缩短而变小，趋近于短时间内的平衡位置。其分布估计也表明，随着周期的缩短，其纵倾及横摇越来越多地集中于平衡位置附近。

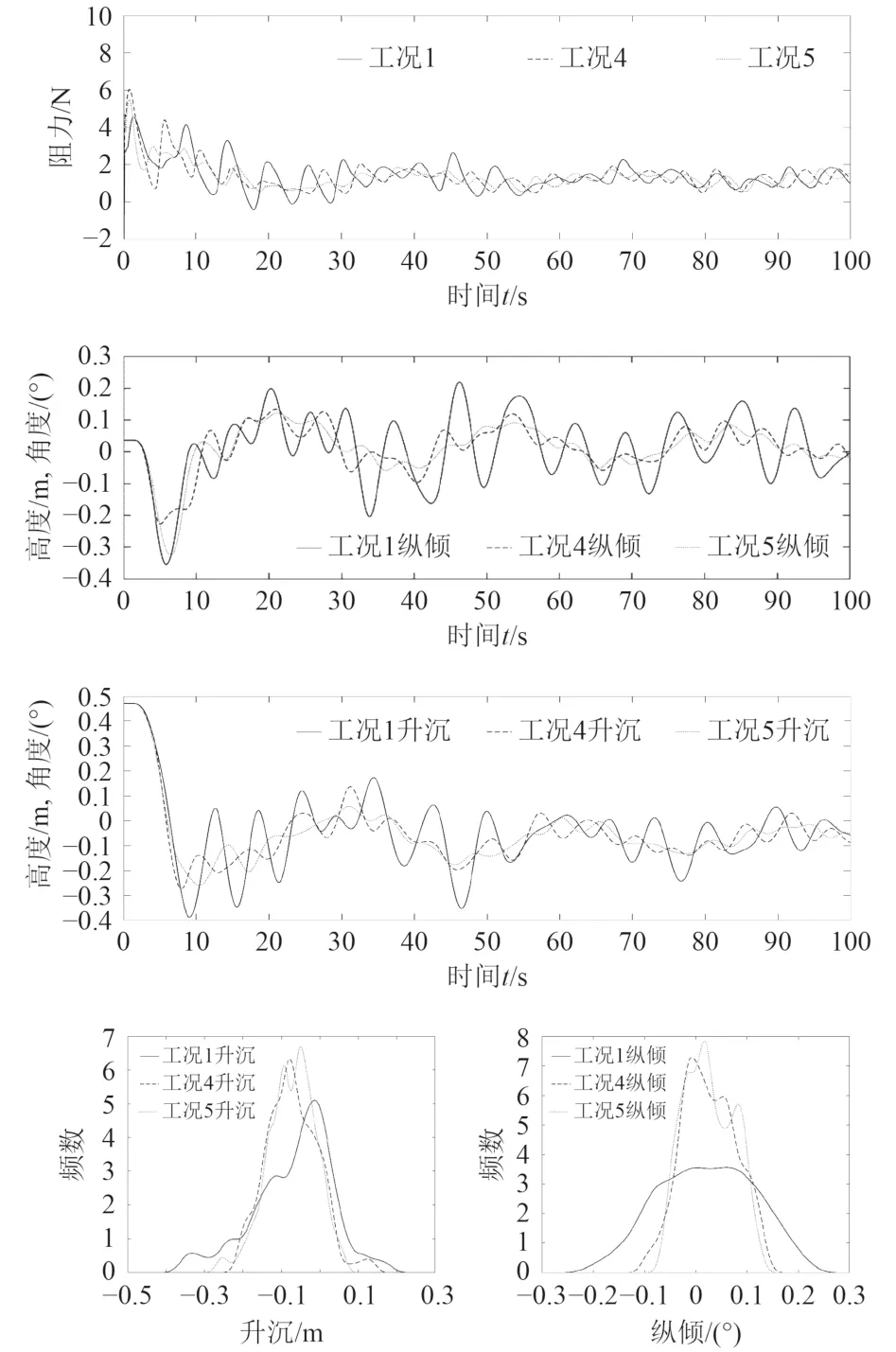
图12 海浪谱峰周期变化下的对比Fig. 12 Comparison of changes caused by wave spectrum peak period

其剪切压差阻力随工况变化如图13所示。

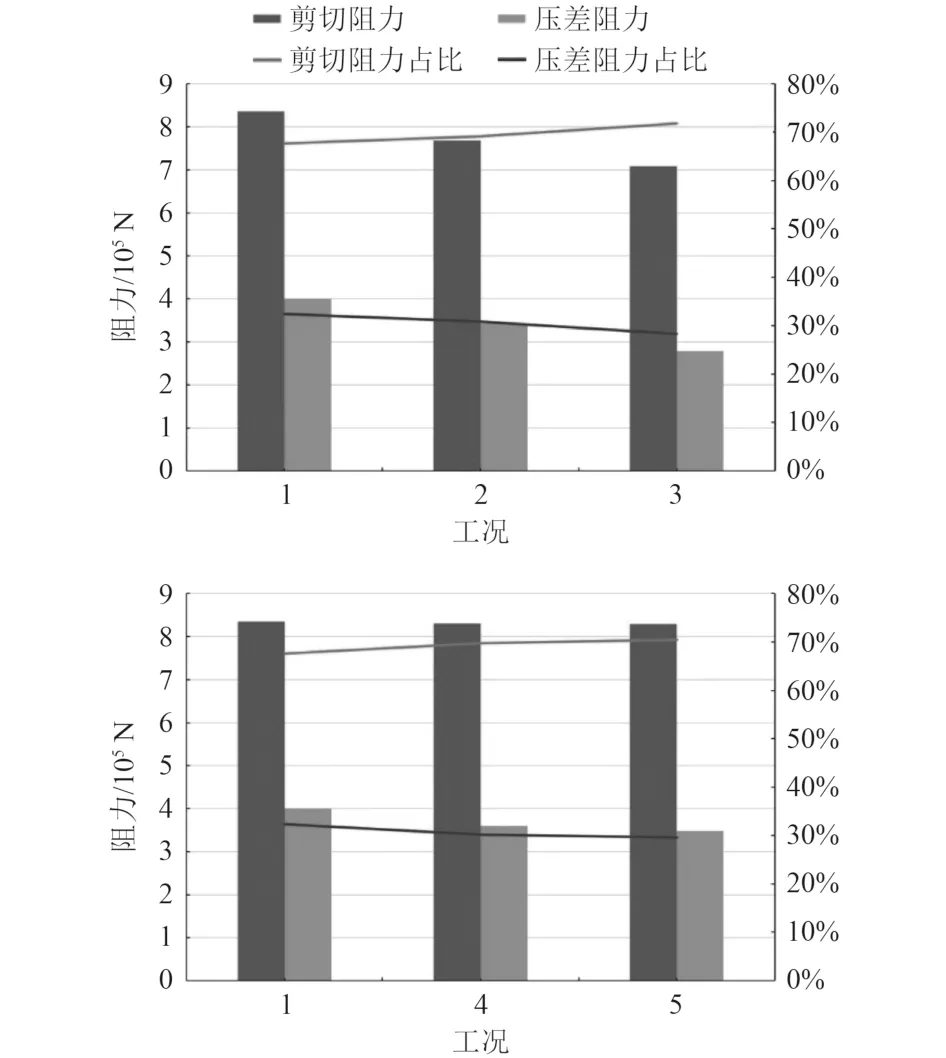
图13 阻力构成占比随工况的变化Fig. 13 Comparison of resistance composition ratio with working conditions

随着海流流速以及谱峰周期的减小，其剪切阻力占比都会增加。海流流速越小，其剪切阻力占比增加的越多，而随着谱峰周期的减小，其剪切压力占比增加的量越少。

5 结 语

1）船舶迎浪航行时波浪起伏造成的船体运动响应其纵倾与升沉变化的周期一致且正负相反，运动响应与阻力变化之间有很大的相关性，但其影响集中于压差阻力，属于船体运动兴波带来的阻力变化，对于剪切阻力影响较小。

2）对于海浪流的迎浪航行在一定程度上会加深吃水且加剧其升沉，对于纵倾影响较小，而波浪周期足够短时更有利于船舶航行的稳定。

3）基于真实海况的实船顶浪航行数值模拟为邮轮耐波性及吊舱的选型奠定了基础，后续可开展基于真实海况的吊舱船体耦合分析。