基于AHP-CRITIC法的半潜式钻井平台主尺度多准则决策

傅 强， 刘笑语， 唐 品， 孟 珣,3*

(1. 中国海洋大学 工程学院， 山东 青岛 266100; 2. 烟台中集来福士海洋工程有限公司， 山东 烟台 264035；3. 山东省海洋工程重点实验室， 山东 青岛 266100)

0 引 言

21世纪，人类进入全面开发利用海洋的新时代。我国近年来逐步加大对海洋资源的勘探、开发力度。大型半潜式钻井平台是深海油气资源开发的主力装备，也是展示国家海洋科技水平、保障海洋权益的国之重器。

半潜式钻井平台的设计和建造难度较大，是典型的高技术、高投入、高风险、高附加值的海洋工程装备，在作业能力、总体性能、抗风浪能力、甲板面积和装载量以及适应水深范围等方面有显著的优势。在平台的设计选型中，需要考虑作业环境、工作能力、经济性等综合因素。尺度规划是设计初始阶段，传统方法大多采用耗时的试算和误差评估，根据初步方案计算平台的相关性能，逐一分析平台的性能指标是否满足设计要求，若不满足，则需根据工程设计经验等修改参数并重新计算相关性能，直至达到设计要求，该办法效率低，且后期相关配套专业改动工作量大。

针对上述问题，国内外学者逐步开展了将工程问题与管理科学和计算机技术应用结合的相关研究。AKAGI等[1]提出采用计算机辅助设计方法获得最优的半潜式平台尺度，将设计转化为非线性多目标优化问题，利用广义约化梯度法进行数值推导得到Pareto最优解集。TAKAGI等[2]采用简化方法计算水动力参数，并用二次规划方法求得半潜式平台在随机海浪下运动最小的平台尺寸。PARK等[3]提出一种用于半潜式浮式生产装置船型优化的全自动程序，运用模拟退火算法得到4个优化方案。彭小佳等[4]根据设计经验对半潜式起重铺管船的船型优化方法及优化过程中应重点考虑的因素、J-Lay塔的布置、船型优化设计过程等方面进行总结，为优化设计提供参考。孟珣等[5-6]综合考虑海上施工、安装、运营的环境影响、经济性能和结构水动力特性，采用多准则评价方法给出Barge、Spar和张力腿平台(Tension Leg Platform，TLP)浮式风电支撑结构的整体工作性能及TLP试验验证。周佳等[7]以半潜式平台垂荡运动最小为优化目标，选择非受控排序多目标遗传算法获得最优解。张艳芳等[8]采用经典的模糊评价方法对自升式钻井平台总体方案进行评价和优选，建立评价指标集，对5个设计方案建立评价矩阵并进行求解，得出最佳方案。QIU等[9]利用人工神经网络预测方法和逆多二次函数(Inverse Multi-Quadric，IMQ)径向基函数建立代理模型以评估不同型式平台的水动力性能，利用粒子群算法获得Pareto最优集。傅强[10]提出一种基于整体工作性能的大型半潜式平台主尺度多目标寻优决策方法，在多准则优劣解距离法(Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS)中引入熵权，建立特定工程问题客观评价矩阵。

综上所述，国内外已经将优化算法应用于半潜式平台的尺度规划中，以获得最优解集。但是，如何合理确定多目标Pareto解集中的最优方案排序研究较少；大多以母型设计判断和以往经验获得最终主尺度方案，缺乏必要的决策数据支撑。本文采用多目标遗传算法(Multi-Objective Genetic Algorithm，MOGA)对第七代半潜式目标平台进行主尺度多目标寻优，并采用AHP-CRITIC(Analytic Hierarchy Process-Criteria Importance Though Intercriteria Correlation)主客观综合赋权法进行综合决策，使最优解既满足决策者的主观期望，又符合各指标之间非一致性的客观判断要求，并将其与现有典型平台方案对比，证明该方法的合理性和高效性。

1 多目标优化

第七代超深水半潜式钻井平台立足于深海油气开发，最大工作水深达3 660 m，比第六代平台增加20%；钻井深度达15 250 m，比第六代平台增加30%；操作工况可变载荷达10 000 t，比第六代平台增加25%。同时实现低能耗、低噪声、高效率，更加绿色环保，适用于中国南海、墨西哥湾、巴西及西非等全球除北海外绝大多数海域。这使结构设计难度达到了前所未有的水平。指标的提升必然带来主尺度的增加，若无限制增加平台尺度，会带来总体和结构性能的问题，易引起平台重量及排水量、设备能力及等级的增加。如定位系统规格的提高、主机及推进器功率提升会使平台造价显著提高、建造难度增大，严重影响平台的经济性。

1.1 综合性能要求

平台主尺度规划需要综合考虑多种因素，尽可能在性能最优与成本最小之间达到最优的配合，是典型的多目标优化问题。根据半潜式钻井平台特点，在优化问题中需要关注的主要性能如下：

(1) 稳性。稳性是半潜式钻井平台设计中的关键性能之一。由于甲板上布置钻井架、管柱等器材，平台的重心较高。如果稳性控制不当，将威胁平台作业安全，因此必须在设计阶段充分考虑其稳性性能。

(2) 垂荡运动性能。垂荡运动性能是钻井平台最重要的性能之一，其运动幅度越小越好。半潜式钻井平台在海面作业时，立管连接平台和海底，而平台的周期性垂荡运动会带动钻柱的垂向运动。运动幅度一旦过大，就会造成井底的钻压变化，甚至导致钻头脱离井底。此外，钻井平台常采用的顶张式立管和干采油树系统，其并不适用于垂荡响应过大的平台，只能采用钢悬链线立管和湿采油树系统，不利于日常的维护和检测，从而增加了作业难度和成本。目前，常用的减小半潜式钻井平台垂荡响应的方法主要有增加吃水、安装垂荡板、采用H形浮箱平台等，但大部分方法是针对四浮体平台设计的。

(3) 气隙性能。对于正常作业的半潜式钻井平台，气隙指波浪距离平台下甲板的最小值，是衡量载体能否正常工作的重要指标。气隙性能差会导致甲板上浪、波浪抨击下甲板等现象的出现，严重影响平台的正常作业和工作人员的安全。前人的各种理论分析和数值模拟都表明，海洋平台的气隙响应会受到诸多因素的影响，包括立柱的长宽度、水线面面积、平台整体的重心重量分布及固有频率、立柱间距等。此外，波浪遇到立柱会发生爬升现象，将波浪前进的动能转化为势能，导致波高在立柱附近异常增加，对海洋平台的安全性产生极大隐患, 因此在设计时须充分考虑气隙大小。

(4) 多海域服役需求。超深水钻井平台的设计环境条件主要考虑中国南海海域的海况，同时兼顾墨西哥湾、西非、东南亚及巴西等主要深水区域。在主要深水海域中，中国南海和墨西哥湾海域台风或飓风条件下极端波浪、风速和流速放大，是平台结构强度设计、定位能力设计等的控制海况条件。

1.2 优化问题的数学模型

在初步设计阶段，应评估平台的工作性能，以保证平台作业的安全性。因此根据设计要求和平台资料，确定设计变量x=(x1，x2,…,xj)的范围及彼此之间的约束，确保气隙hA、初稳心高hGM、垂荡周期Th、纵摇Hp满足要求，以实现最小化平台钢材重量W(t)和垂荡响应Hh的目标。综上所述，平台的优化模型数学表述为

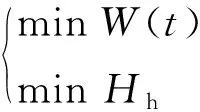
(1)

式中：W(t)为立柱与浮筒钢材重量之和；Hh为平台垂荡RAO峰值；Th为平台垂荡运动固有周期；Hp为平台纵摇RAO第一个峰值；CA,min、CGM,min、CTh,min、CHp,min分别为允许的最小气隙、最小初稳心高、最小垂荡运动固有周期、最小纵摇RAO第一个峰值。

1.2.1 设计变量

主尺度规划往往是海洋平台设计的第一步，对后续水动力性能的影响较大。由于主尺度各参数之间并不是完全独立的，最终根据目标平台的结构选取7个设计变量，具体如图1所示。初始平台参数参照第七代半潜式钻井平台数据，如表1所示。多目标优化中设计变量的变动范围取为初始值的±10%。初始参数、变化范围、常量等如表2所示。

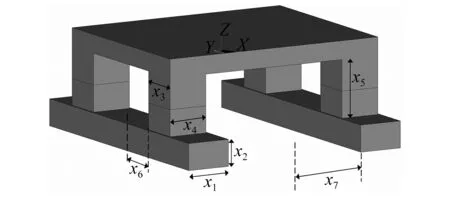
图1 初始半潜式钻井平台湿表面模型

表1 初始半潜式钻井平台参数

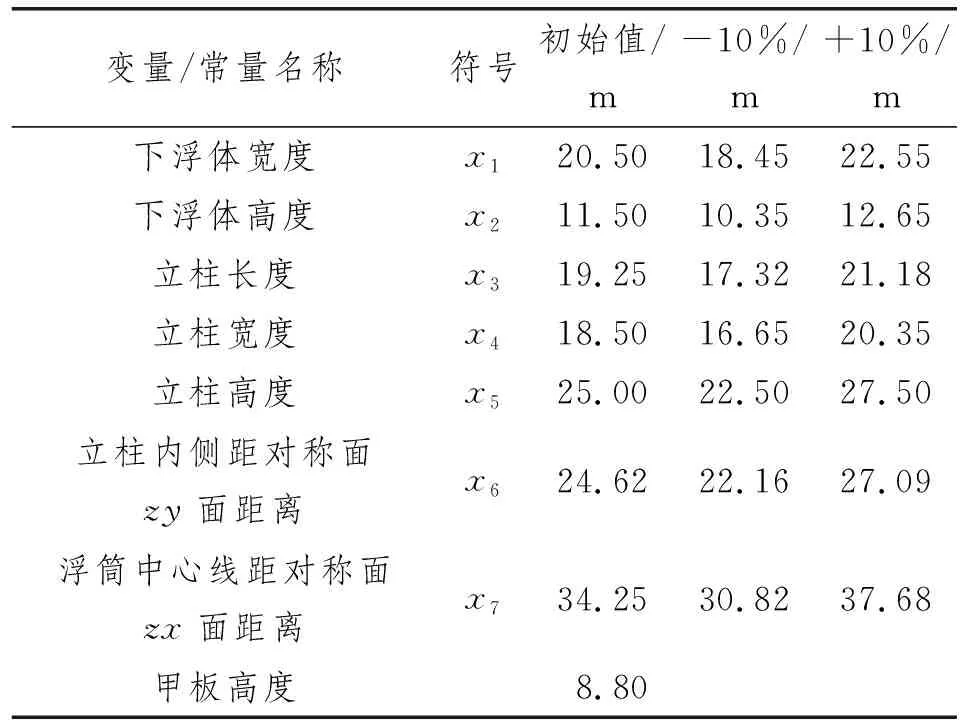
表2 设计变量、常量相关参数

1.2.2 目标函数

为使优化后的半潜式钻井平台最优主尺度方案可以在保证运动响应和稳性的同时具有更低的建造成本，优化目标为平台钢材重量和平台垂荡响应。

(1) 平台钢材重量

半潜式钻井平台生产成本包括钻井设备的价格、钢材成本、船厂的运输成本、安装成本等部分。其中，钢材成本约占总成本的一半。因此，合理减少钢材用量对于降低成本而言具有重要意义。PENNEY对许多已有或在建的海洋平台进行数据统计分析，把平台分为下浮体、立柱、甲板等几个部分，得到半潜式钻井平台各部分钢材重量估计公式。

① 下浮体钢材重量

W1=9.4×10-3(SpT)1.05

(2)

Sp=2Lp(Bp+Dp)

(3)

式(2)和式(3)中：W1为单个下浮体钢材重量；Sp为下浮体的表面积；T为作业吃水，即下浮体高度x2；Lp为下浮体长度；Bp为下浮体宽度x1；Dp为下浮体高度x2。

② 立柱钢材重量

PENNEY认为，可将截面带圆角的矩形近似为矩形进行计算，则：

W2=0.286HcBc1.612

(4)

式中：W2为单个立柱重量；Hc为立柱高度x5；Bc为立柱宽度x4。

③ 甲板钢材重量

(5)

式中：W3为甲板钢材重量；Am为主甲板面积；Ar为其他甲板面积，假设其与主甲板面积相等；HD为甲板高度。考虑到甲板面积与上部结构的布置有关，在估算平台重量时，甲板钢材重量不计入主尺度优化过程。

将各个下浮体、各个立柱钢材重量相加，即可得到半潜式钻井平台的钢材重量，作为优化的目标之一。

(2) 垂荡运动幅值

半潜式钻井平台在垂荡方向只允许较小范围的运动响应，通常不超过2 m。在通常情况下，主尺度一旦确定，往往垂荡性能就会基本确定，重心位置、转动惯量等参数的调整通常只会影响平台的纵摇、横摇等。且相对于纵摇、横摇等，垂荡运动对于上部结构的可操作性起着决定性作用。因此，更关心目标平台的垂荡性能。

1.2.3 约束函数

(1) 垂荡固有周期

垂荡性能是主尺度优化阶段重要的考虑因素，由于半潜式钻井平台在垂荡方向允许的灵活性比较小，且要求平台的垂荡运动固有频率尽可能低于设计波浪谱峰频率，因此根据DNV-RP-F205建议，平台的垂荡固有周期不小于20 s。

(2) 纵摇第1个峰值

纵摇固有周期一般明显大于可能遇到的波浪周期，纵摇第1个峰值不大于5°。

(3) 气隙性能

平台的瞬态气隙可以表示为

δ(t)=δ0-ηrel=δ0-[ζ(t)-ηver(t)]

(6)

式中：δ0为海洋平台的初始气隙；ηrel为平台甲板下方任意一点P处的波面升高值；ζ(t)为P处的时域下波高；ηver(t)为平台甲板在相同位置P处的垂向位移。

因此，对于新建浮式平台，根据API-RP-2FPS推荐，极端工况下的净气隙不小于1.5 m，生存工况下的气隙大于零。

(4)初稳心高

在平台的主尺度设计阶段，可将初稳心高作为衡量平台稳性的指标。根据中国船级社(CCS)规范建议，海上浮式移动平台的初稳心高应不小于0.15 m。

1.2.4 多目标遗传算法

优化算法采用MOGA，该算法是基于受控精英概念改进的非支配排序遗传算法(NSGA-Ⅱ)的一种变体，支持多个目标和约束，旨在找到全局最优值。算法流程如图2所示。

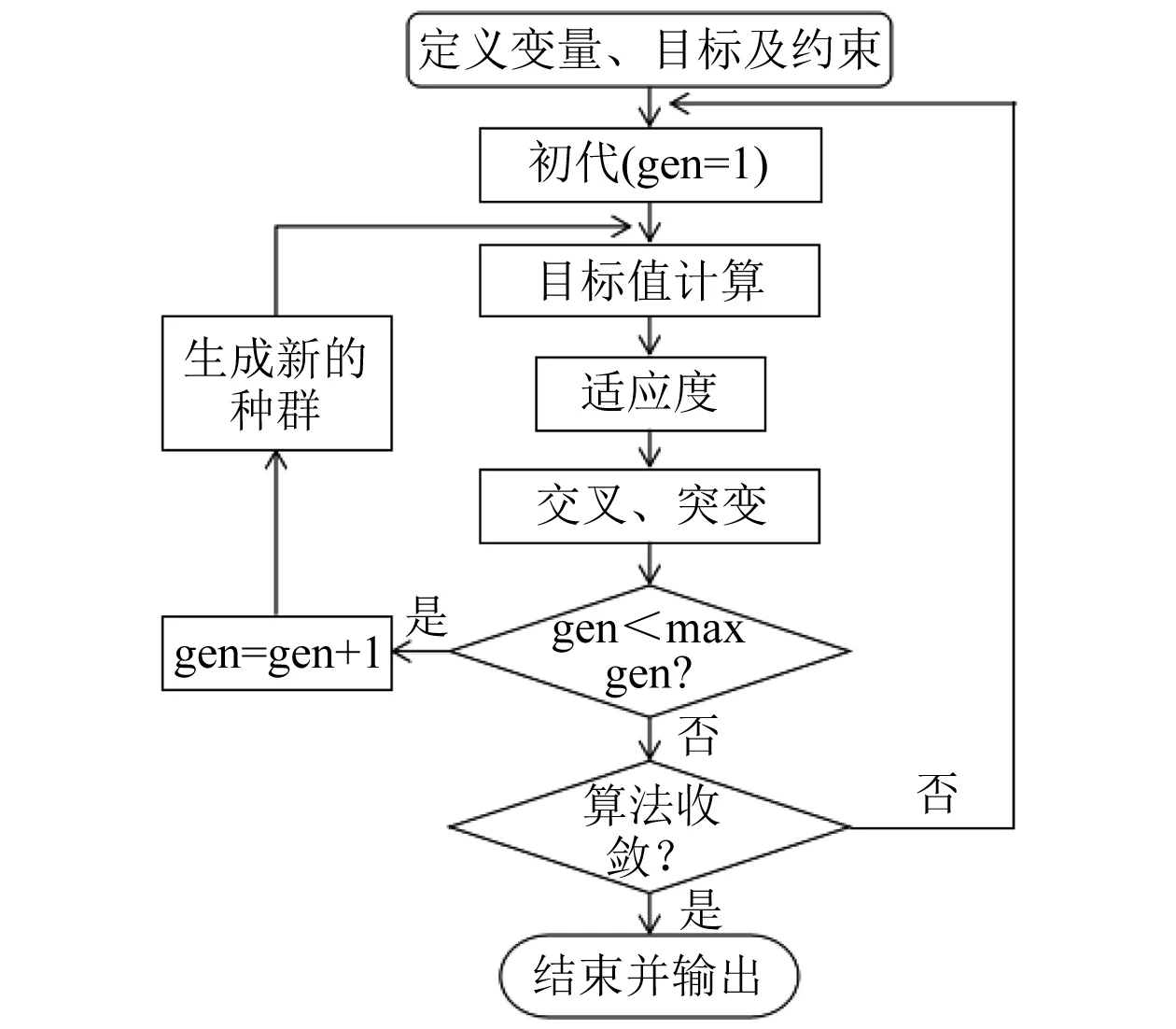
图2 MOGA算法流程

1.3 优化结果分析

采用AQWA和Design Exploration模块进行水动力性能数值模拟和多目标优化。按照表2数据设置输入变量及变化范围，采用响应面优化设计法通过建立简单的数学关系来表示工程问题中设计变量与输出变量之间的非线性关系。在得到响应面后，采用MOGA进行优化。样本点初始样本数量为1 000个，每次迭代样本数为50个，最大允许Pareto百分比为70%，候选样本数为3个。最终得到3组候选主尺度方案(见表3)及目标函数Pareto图(见图3)。由表3可知，3组方案的大部分水动力性能指标优于初始方案，且钢材用量更少，降低了成本，证明该优化方法的可行性和可靠性。

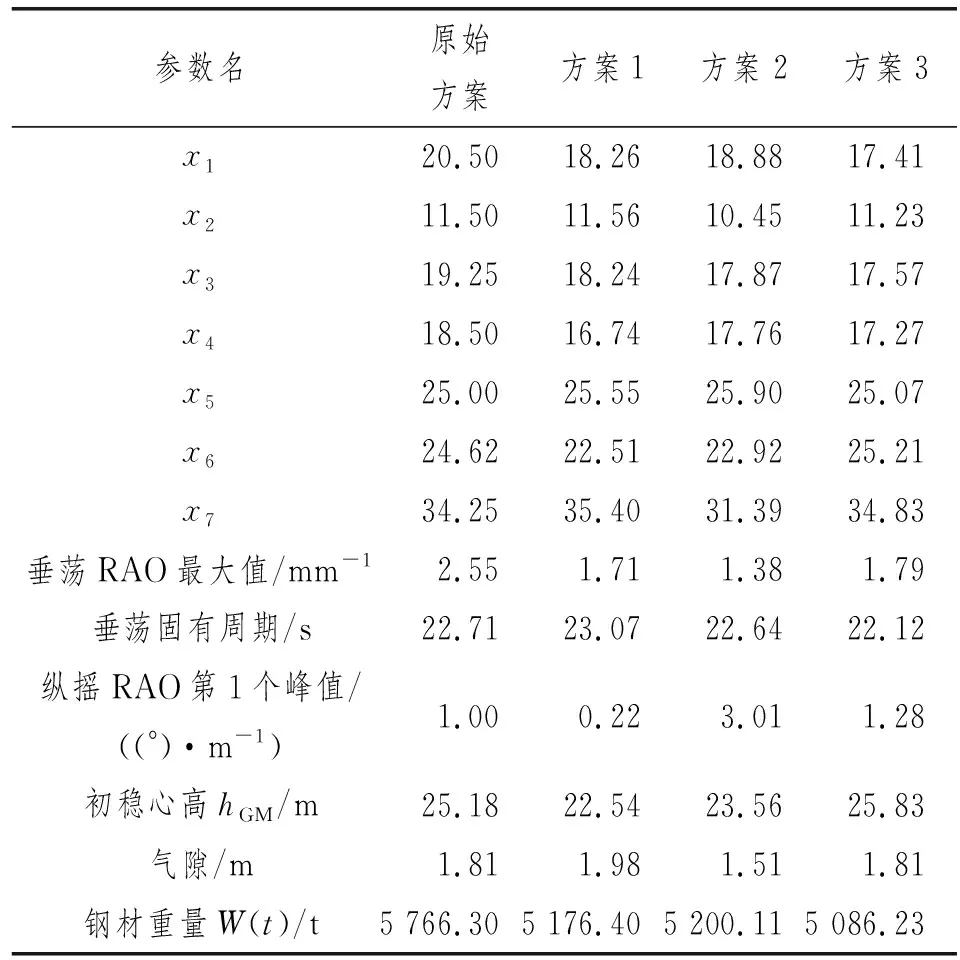
表3 原始方案与候选方案对比

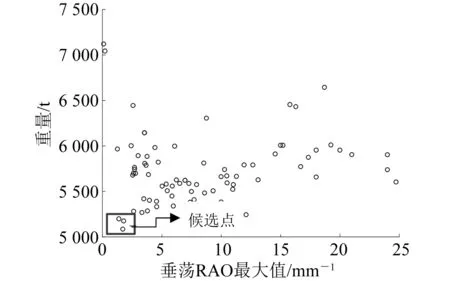
图3 优化目标Pareto图

图4描述了50组候选方案中立柱内侧距对称面zy面距，即表征半潜式钻井平台同一浮体上立柱间距x6的相对大小。由于在本模型中立柱间距影响着下浮体的长度，从而间接影响了钢材成本，因此应尽可能减小x6。但在实际上，立柱间距的增加有利于平台稳性的提高。但是在本次优化模型中，由于大部分设计点的hGM均在20 m以上，远高于约束函数中0.15 m的标准，因此提高稳性不作为优化的首要目的。从降低成本的角度考虑，更小的立柱间距有利于减小建造成本。

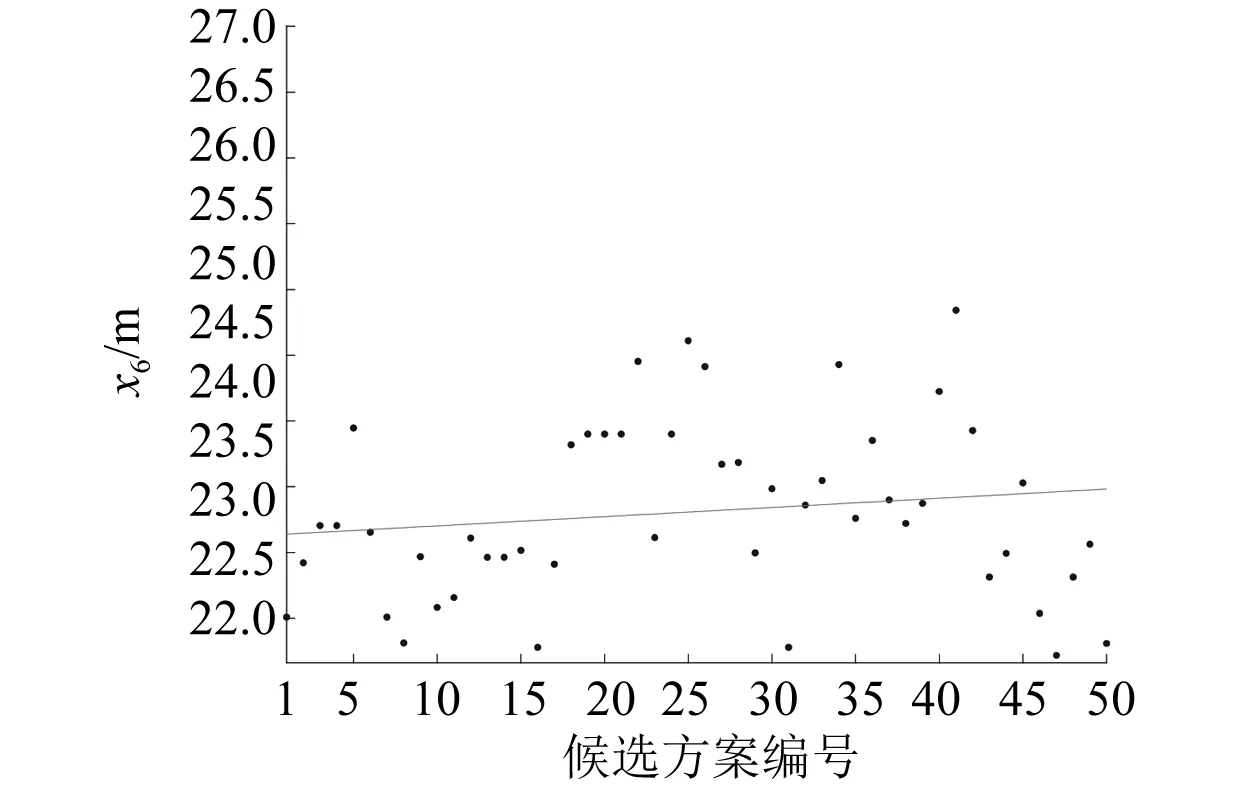
图4 x6在候选方案组中的分布情况

图5描述了50组候选方案中立柱宽度x4的相对大小。由于在本模型中立柱的宽度影响着钢材成本，且二者成正比，因此从降低成本的角度考虑，应尽可能减小x4。从安全性的角度考虑，增加立柱宽度有利于增加水线面面积，从而提高平台的稳性。但是在本次优化模型中，同样由于大部分设计点的hGM均在20 m以上，远高于约束函数中的0.15 m的标准，因此提高稳性不作为优化的首要目的。从降低成本的角度考虑，更小的立柱宽度有利于减小建造成本。

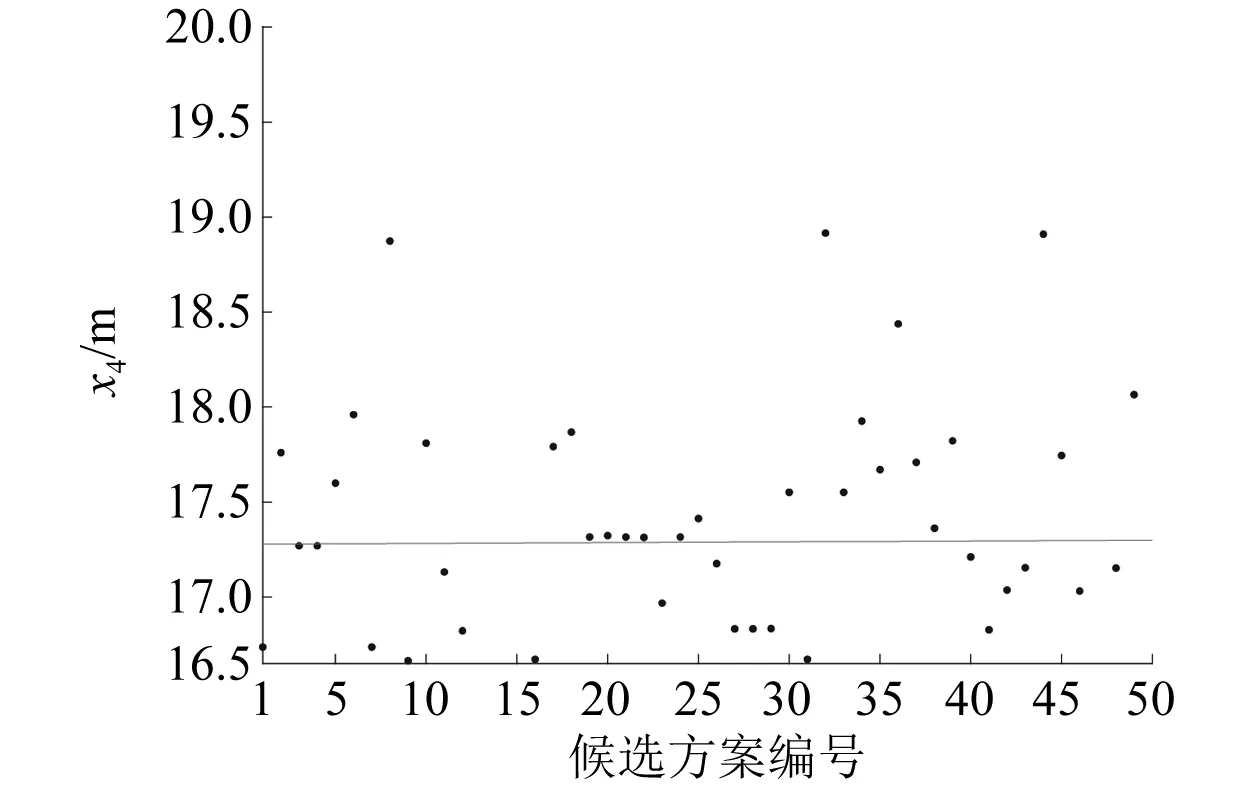
图5 x4在候选方案组中的分布情况

图6描述了x1～x7对于垂荡RAO最大值的局部灵敏度。由图6可知，增加立柱的长、宽有利于减小平台的垂荡响应最大值，这是因为立柱的水线面面积得到增加，从而增加平台的静水恢复力，减小垂荡响应。然而，增加下浮体的宽度和高度、立柱高度会导致平台的垂荡响应显著增加，这是由于本优化模型定义结构的质量为定值，排水体积的增加会导致吃水减少，从而增加垂荡响应。解决方法之一是增加压载水量，从而增加整体平台重量，在垂向外力不变的情况下减小垂荡加速度、增加吃水。因此，在实际工程问题中，可通过采用增加压载水量的方法减小平台的垂荡响应。

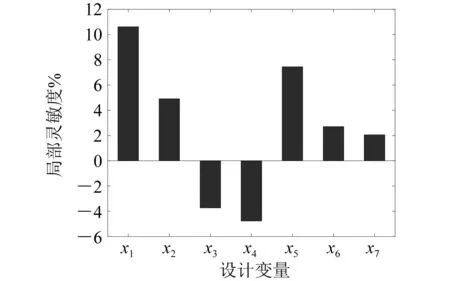
图6 垂荡RAO最大值的局部灵敏度

2 多准则决策

2.1 AHP法确定评分权重系数

层次分析(AHP)法将定量与定性分析结合，先由决策者衡量各优化目标之间的相对重要性，再合理地计算出其标准权重，并以此进行优劣排序。

AHP法确定权重系数的步骤如下：(1) 将实际问题按照决策目标、约束条件、候选方案分为3个层次；(2) 两两比较中间层中各指标的重要性，并生成判断矩阵；(3) 计算判断矩阵的特征值和权相量；(4) 一致性检验。

在本模型中，中间层为半潜式钻井平台纵摇响应最大值、垂荡响应最大值、钢材用量，生成判断矩阵A为

(7)

计算得最大特征值λmax=3.009 2，将其特征向量标准化后，得到权向量为

U=[0.126 01,0.416 06,0.457 93]T

(8)

一致性指标IC为

(9)

式中：n为指标的数量。查随机一致性指标表(见表4)可得，IR=0.52，则一致性比率RC为

表4 随机一致性指标IR表

(10)

因此，一致性良好，得到各评价指标的主观权重，如表5所示。

1.2.5 考核 每项基本操作培训后，均要进行考核，操作合格分为90分，对护士操作中存在的不足，进行当场点评，保证操作的规范。对健康档案的建立与更新，均进行上机考核，了解护士操作熟练与正确程度，评分标准参照公共卫生考核标准，合格分为100分。

表5 AHP法得到评价指标的主观权重

2.2 CRITIC法确定评分权重系数

CRITIC权重分析法是通过2个客观因素判断各数据的权重：第一个是对比度，基于标准离差法，如果某个指标的标准差越大(即同一指标的所有备选方案的差别越大)，则认为该优化条件包括的信息量越大；第二个是指标之间的矛盾性，用2个指标之间的相关系数来衡量，如果其呈现正相关，则矛盾性较低。

(11)

其中，

(12)

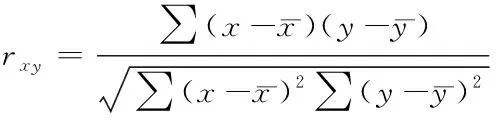
(13)

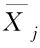
(14)

将原数据经过无量纲化处理后得到其相关系数矩阵为

(15)

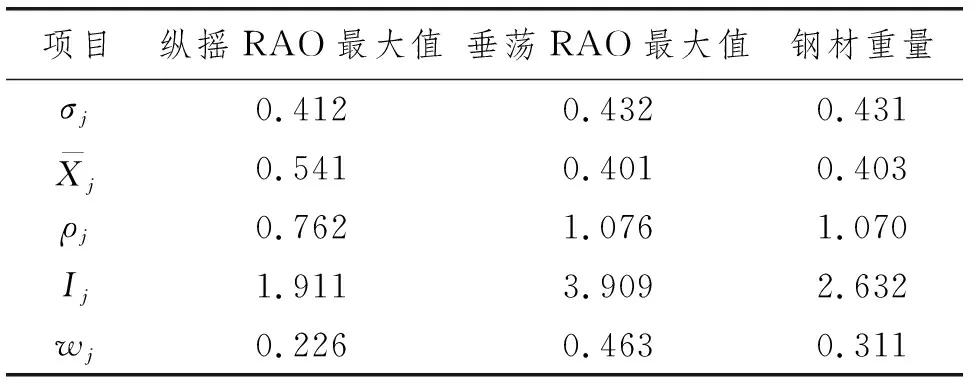
表6 各评价指标的权重系数及中间结果

2.3 AHP-CRITIC法确定综合评分权重系数

为得到一组既反映决策者主观意愿又考虑客观模型属性的权重系数，采用AHP-CRITIC法综合考虑各指标权重系数。具体公式为

(16)

式中：wj,A为通过AHP法得到的权重系数；wj,c为通过CRITIC法得到的权重系数。

由此可以得到AHP-CRITIC法综合赋权的各项评价指标的权重系数，如表7所示。

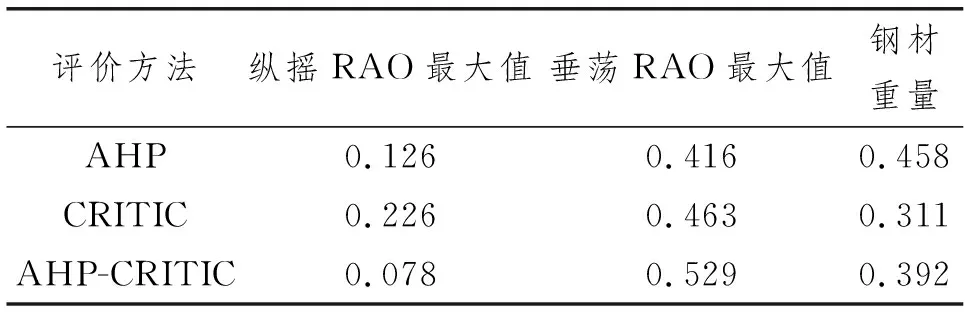
表7 3种方法得到的权重系数

对3种方案的各项指标进行无量纲化处理，即可得到各方案的评分，如表8所示。

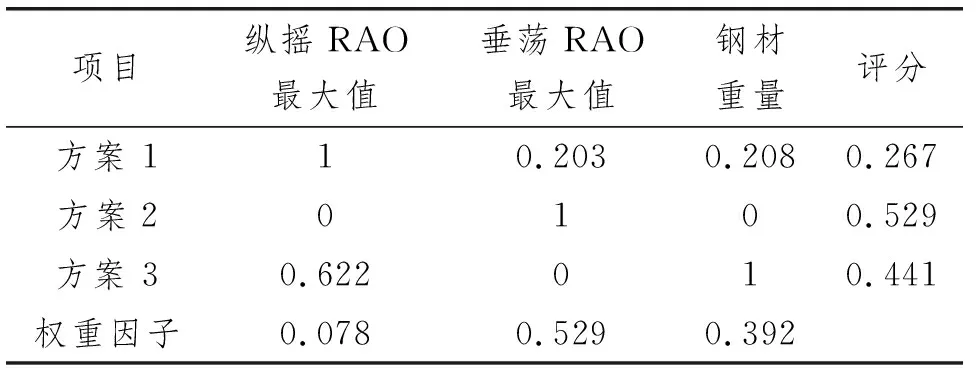
表8 采用AHP-CRITIC法得到的各方案评分

采用SPSS 20.0软件对结果进行分析，CRITIC法得到的权重与AHP法得到的2种权重的相关系数r=0.7，较为接近1，且P值(Pearson’s correlation coefficient)为0.517，说明两者相关性不显著(P>0.05)，即2种赋权法反映的内容相互独立，不具有重复性。

综上所述，AHP-CRITIC法具备主观和客观上的合理性，使结果既满足决策者的主观期望，又符合各指标之间冲突性和对比强度。因此，对于目标平台而言，方案2中的主尺度参数可使平台同时具有相对更低的建造成本和更优的水动力性能。

表9比较了最优方案与原始第七代半潜式钻井平台方案的3个主要尺度参数。由于以减少钢材成本作为主要优化目标之一，因此整体平台优化后的长度和宽度有明显减小；但整体垂向高度变化不大，说明减小平台高度对于整体平台钢材重量的影响并不显著，同时出于平台的安全性及吃水考虑，平台高度不应过小。

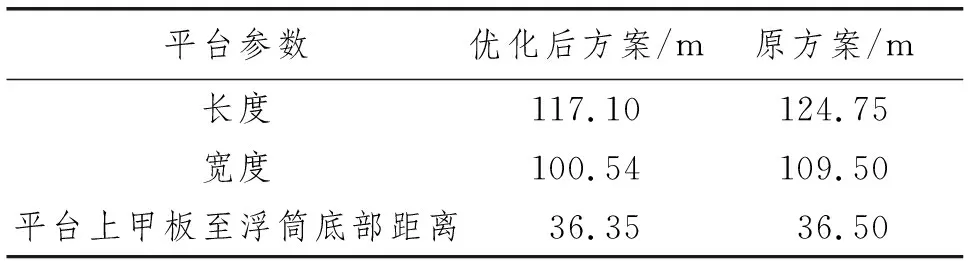
表9 最优方案与第七代半潜式钻井平台方案对比

3 结 论

利用参数化建模技术，基于深水钻井平台布局规划原则及方案综合性质，建立半潜式钻井平台简易模型，在满足平台初稳性、气隙等设计要求的情况下，快速地得到满足垂荡水动力特性及最小用钢量的主尺度的最优解集，并引入多准则决策概念，科学地决策以得到平台的主尺度方案，该优化寻优方案结构主尺度与现有第七代半潜式钻井平台方案的主尺度对比小于10%，证明基于综合性能的自动寻优决策方法的高效性，可应用于实际项目的工程选型设计。具体结论如下：

(1) 采用响应面设计法和MOGA对半潜式钻井平台的主尺度参数进行优化设计，运算精度较高、速度较快；可同时考虑到建造成本和水动力性能之间的关系，找到相对最优的候选方案，克服单一目标的局限性。

(2) 对于稳性有较大裕量的半潜式钻井平台，可通过减小立柱宽度、同一浮体上立柱间距的方法来显著降低建造成本。增加下浮体的长度和宽度可减小平台的垂荡响应。此外，深吃水也是减小垂荡响应的有效方法。

(3) 采用AHP-CRITIC法对方案进行多目标决策，同时考虑决策者的主观意愿和不同指标之间的客观对比度和矛盾性，将两种赋权方法结合，增强了评价结果的科学性，减小了单一评价方式造成的误差。