海底管道端部行走评估的解析方法

崔少敏， 夏日长， 李 庆， 雷震名， 赵 党

(海洋石油工程股份有限公司， 天津 300451)

0 引 言

随着我国海洋油气田开发逐渐走向深水，输送高温高压介质的海底管道建设日益增多。高温高压海底管道产生较大的轴向膨胀和轴向力，易导致管道端部行走现象的发生[1-2]。过高的端部行走量会对管道端部海底结构物如井口设施、管汇或立管等造成损害，从而引发管道破坏和泄漏，导致海洋环境污染和重大经济损失。因此，海底管道端部行走行为的评估对深海油气田开发具有十分重要的意义。

目前，国外学界及工程界对于海底管道行走分析技术进行一定的理论研究。GAILLARD等[3]研究西非深水海域中黏土区管道设计中的海底管道行走模式，对包括由海床斜坡导致的行走、热瞬态导致的行走、布线弯曲不稳定导致的行走、行走与侧向屈曲相互作用导致的行走等4种海底管道行走模式进行分析，并给出潜在的解决方案。BRUTON等[4]探究管道侧向屈曲与管道行走的相互作用，对单层管和双层管系统中管道屈曲及行走所采用的解决方案进行描述与讨论。TORNES等[5]对海底管道轴向行走进行研究，通过大量非线性有限元分析，探究管道轴向行走机理，并对限制此类行走的方法进行阐述。BRUTONG等[6]将分析研究与模型试验结合，论述管道-土壤相互作用对易发生侧向屈曲和管道行走的海底管道设计的影响。

国内对于该领域的理论研究尚处于起步阶段，数个相关项目均采用有限元法对管道行走进行评估。虽然该方法更贴合实际，但模型复杂、计算周期长等原因使该方法并不适用于可行性研究阶段、基本设计阶段等项目前期的初步评估。因此，研究能提供管道行走行为快速评估的数值解析方法十分迫切且具有重要的工程意义。

1 海底管道行走评估解析方法

1.1 海底管道行走行为筛选

当海底管道启动时加热加压，管道沿轴向会发生膨胀。当管道关停时冷却收缩，受海床摩擦阻力的影响，管道两端可能不会收缩回到原来的位置。伴随启动和关停的循环，管道会产生全局轴向移动。这种管道全局轴向移动被称为管道行走。

行走是一种发生在短、高温管道的现象。术语“短”是指在膨胀过程中管道中间位置未达到全部约束，相反“长”是指在膨胀时管道中间存在虚拟固定段。随着管道操作温度的升高，短管道长度可达数公里。行走现象也可发生在已发生侧向屈曲的较长管道。

通常管道膨胀现象通过沿管道分布的有效轴向力进行定义。管道内的有效轴向力由管壁轴向力和压力引起的轴向力组成，定义为

S=SW+peAe-piAi

(1)

式中：S为有效轴向力(文中提到的轴向力都为有效轴向力)；SW为管壁轴向力；pe为外压；Ae为管道外截面积；pi为内压；Ai为管道内截面积。这里张力为正。

对于两端完全自由释放无约束的管道，管道中的轴向应变为零的力被称为完全无约束有效力，定义为

P=SL-(piAi)(1-2v)-EAα(θ-θinst)

(2)

式中：P为完全无约束有效力；SL为残余敷设张力；v为泊松比；E为弹性模量；A为管道截面积；α为热膨胀系数；θ为操作温度；θinst为安装温度。

对循环加载的管道，在完全约束力卸载情况下式(2)更新为

ΔP=-(p2-p1)Ai(1-2v)-EASα(θ2-θ1)

(3)

式中：ΔP为完全无约束有效力增量；下标1和2表示操作前后变化。

通过完全无约束有效力增量可计算得出发生行走管道的临界循环约束力为

(4)

式中：f*为临界循环约束力；L为管道长度。

一般认为当管道摩擦力f=μW(式中：μ为管道与海床之间的摩擦因数；W为管道水下重)小于f*(即f/f*<1)时，管道被认为是自由移动的。此时管道可被定义为“短”管道，此类管道易发生行走。

在初次循环中，f/f*>2的管道可被认为是全约束的。全约束段将有效地防止管道行走，除非在后期循环中热力曲线梯度非常高。

1.2 海底管道端部行走量评估

管道行走评估需考虑的一个重要问题是油气流的方向及由此产生的热瞬态。通常将距井口或管汇最近的管端称为热端，而接收设施或立管处的管端为冷端。在热瞬态载荷作用下行走的方向通常朝着管道的冷端。

该解析评估方法考虑如下前提假设：(1) 瞬态温度为线性分布，整个升温过程中热梯度为常数；(2) 不考虑内压变化；(3) 不考虑轴向摩擦滑动位移；(4) 管道可以完全移动；(5) 管道轴向摩擦力小于管道膨胀引起的有效轴向力；(6) 仅考虑第2次和随后循环加热。

使用k个等步长的xA对管道行走过程进行模拟，考虑k个增量步后，管道的热锚固点从管道入口到达管道中间位置kxA。此时管道内介质温度在xθk处降至等于环境温度。可根据热瞬态第k-1增量步至第k个增量步的轴向力变化以及沿管道的应变和位移变化方程确定管道的行走位移。由于锚固点处管道位移为零，此时仅管道的加热长度xθk未知，可推导得出管道加热长度计算公式为

(5)

式中：xθk为管道加热长度；k为增量步个数；xA为增量步步长；xθk-1为第k-1个增量步管道加热长度；fθ为热驱动力。

假定管道初始加热长度等于增量步步长，即xθ0=xA。当xθk确定后，管道中间位置的位移为

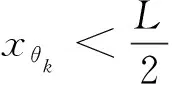
(6)

式中：Δwk为第k个增量步管道行走量。

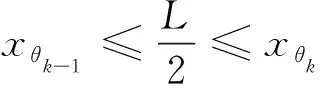
(7)

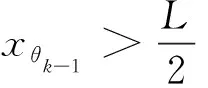
(8)

在热冷却循环中由热瞬态所导致的管道行走可表达为

(9)

式中：Sw为单个循环内总行走量。

当fθ/f≥1.5时，式(6)～式 (9)可简化为

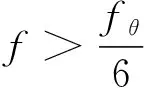
(10)

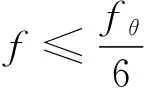
(11)

式(10)和(11)中：fθ=EAαqθ，为热梯度驱动力；qθ为热力梯度。

2 数值算例

中东某项目海底管道参数如表1所示。

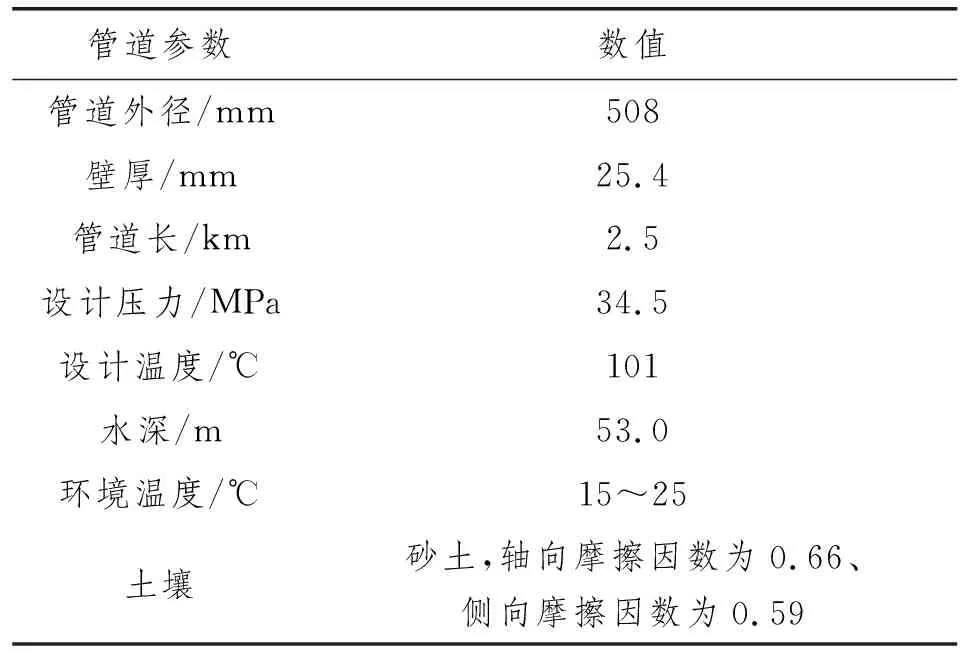
表1 管道设计参数

使用2组再启动温度曲线：热启动温度曲线和冷启动温度曲线。曲线分时图如图1和图2所示。

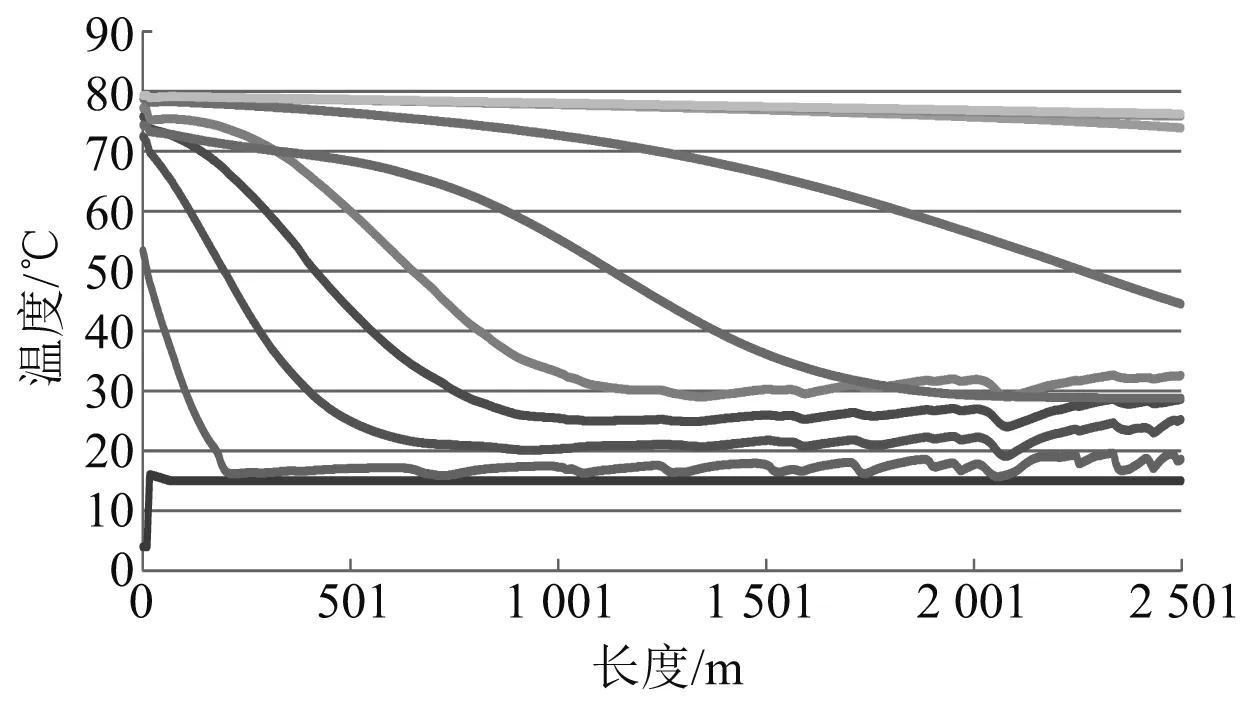
注：自下而上分别为t=0,1,5,10,20,40,60,80,120,240,360 min曲线图1 热启动管道温度曲线

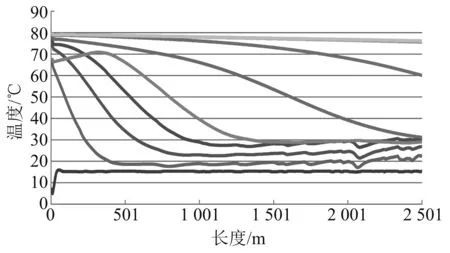
注：自下而上分别为t=0,1,5,10,20,40,60,80,120,240,360 min曲线图2 冷启动管道温度曲线

2.1 解析法计算结果验证

单次重启动过程分别使用热启动和冷启动两组温度数据进行计算。在整个设计寿命内重启动行为发生40次。同时，为验证解析法结果有效性并计算误差，使用Abaqus软件对相同工况下的海底管道行走进行有限元模拟。建立管道全尺寸模型，海床模拟采用指数刚度模型。计算结果如表2所示。

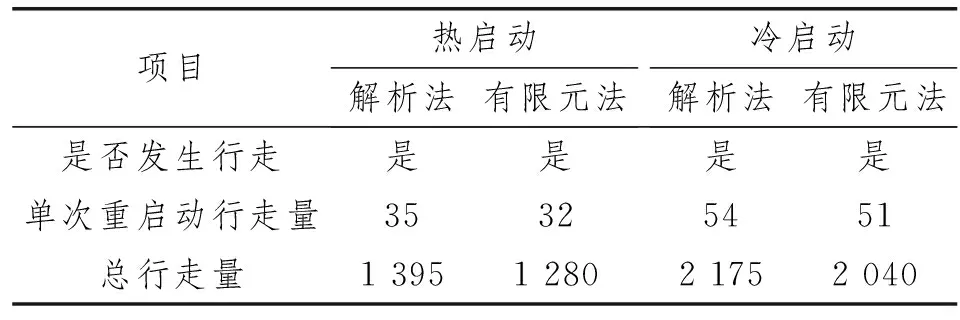
表2 解析法和有限元法计算结果 mm

由表2可知：热启动时解析法与有限元法的总行走量误差为9.0%；冷启动时解析法与有限元法的总行走量误差为6.6%。两者结果差异小于10%，且解析法结果大于有限元法，较为保守。因此，解析法能较有效地评估管道行走行为。同时，冷启动行走量远大于热启动行走量，因此在管道实际运营中应尽可能减少冷启动次数。

2.2 参数敏感性分析

考虑到行走计算中部分参数对行走行为起到至关重要的作用，使用解析法对管道长度、摩擦因数和热力梯度进行敏感性分析。

2.2.1 管道长度敏感性

计算1～6 km长度的管道行走量，增量步为1 km。计算结果如表3所示。

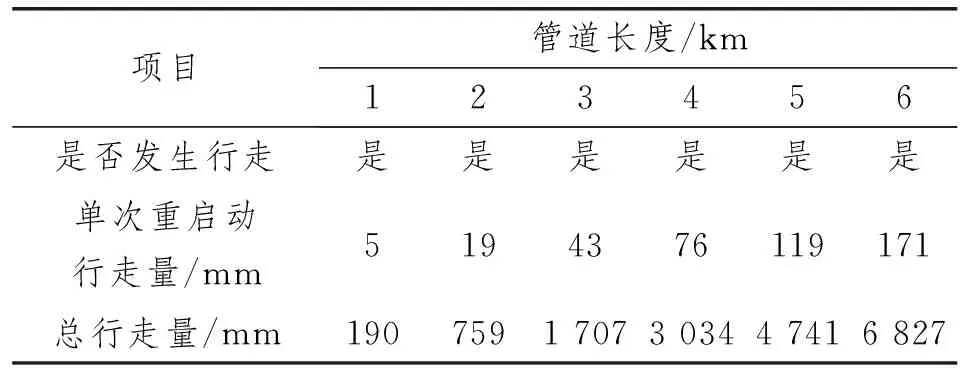
表3 管道长度敏感性分析结果

由表3可知，在发生管道行走前提下，管道行走量随管道长度增长而变大。但需注意当管道长度增长到一定值时，管道行走的驱动力可能不足以克服摩擦力，从而管道不会发生行走。

2.2.2 摩擦因数敏感性

计算土壤摩擦因数为0.2～0.8时的管道行走量，增量步为0.1。计算结果如表4所示。

由表4可知：管道行走量随着摩擦因数增大呈抛物线形状变化；在某个摩擦因数下，管道行走量达到峰值。究其原因是海底管道在渐增的轴向摩擦因数下，轴向约束由完全自由渐变为循环约束，最终至全部约束的过程。

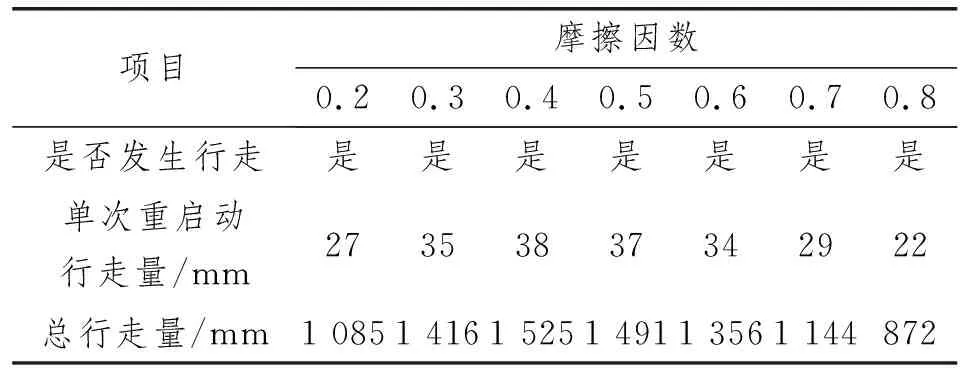
表4 摩擦因数敏感性分析结果

2.2.3 热力梯度敏感性

计算热力梯度为15～30 ℃/km的管道行走量，增量步为2～3 ℃/km。计算结果如表5所示。

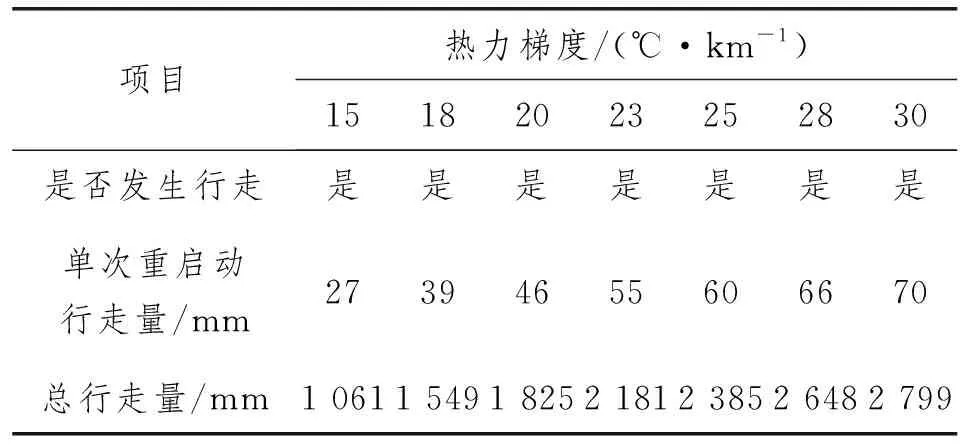
表5 热力梯度敏感性分析结果

由表5可知，管道行走量随着热力梯度变大而增加，大约随热力梯度呈线性增加。因此，建议在管道启动操作时，尽可能控制管道上的热力梯度为最小。

3 结 论

提出一种基于解析方法的海底管道端部行走评估方法，并进行有限元模型验证，对部分关键参数进行敏感性分析，得到以下结论：

(1) 该方法略保守，计算结果与有限元方法差异小于10%。该方法可用于项目前期初步评估海底管道端部行走行为，更精确的结果可在项目后期使用有限元方法分析得出。

(2) 管道越长(在发生管道行走的前提下)，热力梯度越大，管道行走量越大；随海床土壤摩擦因数增大，管道行走量呈抛物线变化。因此，为抑制海底管道行走，可相应采取管道在布线中锚固、管道在启动前预热或其他增加轴向摩阻力等措施。同时对于预期行走问题严重的管道，建议在项目早期进行必要的土壤试验和模型试验，进行更全面的管-土相互作用评估，以准确评估海底管道端部行走行为，避免过度保守设计，降低项目成本。