数据驱动的湍流标量混合非闭合深度学习模型
◆于建
数据驱动的湍流标量混合非闭合深度学习模型
◆于建
(辽宁工程技术大学信息化与网络管理中心 辽宁 123000)
借鉴物理信息深度学习和深隐藏物理模型,提出一个从噪声的时空概率密度函数测算中辨识湍流模型的框架。该模型适用于由运积单点概率密度函数方程描述的条件Fickian标量期望扩散或耗散。采用均匀湍流二元标量混合的振幅映射闭包/Johnsohn-Edgeworth变换模型获得精确解,对所构建的模型进行了测评。
概率密度函数模型;湍流混合;模型辨识;深度学习
湍流标量混合问题在近几十年得到学术界广泛研究和应用[1-3]。在Reynolds-averaged Navier-Stokes(RANS)模拟中,湍流的输运概率密度函数(PDF)明确地描述了这一问题。对于单点PDF描述子, Fickian标量的混合作用表现为:条件期望耗散项和/或条件期望扩散项为非闭合的[2]。通过概率滤波密度函数(FDF)在大涡流模拟(LES)中也遇到了类似的非闭合问题[4]。相关非闭合项的闭包开发已成为热点研究问题。湍流模型的首要目标是为PDF/FDF输运方程中出现的未闭合项找到精确的闭包。在湍流建模中,常采用封闭项表达非封闭项。这种闭包的形式是基于对已有问题的物理检查,它本身就容易出错。这是湍流闭合过程中建模不确定性的主要来源。
本文介绍了一种新的湍流标量混合闭包方法,即从高保真度观测中学习非闭合项。这种观察可能来自直接数值模拟(DNS),如文献[5-7];或时空分辨实验测量,如文献[8-9]。显然,在DNS中,未闭合项可以直接从模拟结果中提取出来。然而实际应用中执行DNS成本过高。另一方面,从实验数据中寻找闭包涉及从实验数据中获取时空和分解空间的导数(在某些情况下是高阶导数),难度较大,且易因时空测量的分辨率引入新的闭包不确定性。本研究的最终目标是开发一个闭包发现框架,从稀疏的高保真数据(如实验测量)中学习闭包。上文中所提出的框架用一种数据驱动的方法取代了常用的“猜测”方法。该方法以系统的方式从数据中揭示出封闭性。本研究方法以偏微分方程深度学习[10]和数据驱动建模策略[11],特别是基于物理学的深度学习[12]和深层隐藏物理模型[13]为理论基础。
二进制标量混合常用在PDF闭包开发中[14-15],本研究中以它为演算实例。该问题通常出现在设置空间均匀流研究中,其亦考虑标量PDF的时间传输。在这种情况下,亟须开发一个能够准确预测PDF的演化的闭包框架。这个问题相对简单,适合DNS和实测实验。文献中有大量通过这些方法获得的数据[5-7,16-23],测评结果表明:本文提出的计算模型学习获得的条件期望耗散和扩散可靠性高误差小。
1 二元标量混合


其中竖线表示条件值。式(1)也可表示为:
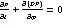
其中表示条件期望扩散:


2 深度学习解决方案
2.1 条件期望扩散
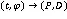
从上述设定及公式(3)可获得以下物理信息神经网络(见图1)。


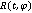
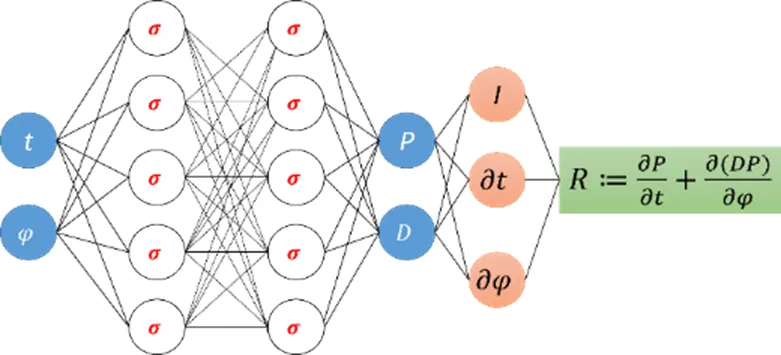
图1 条件期望扩散的物理信息神经网络示例

2.2 条件期望耗散



3 测试评估

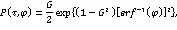


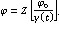
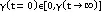



4 结果评估与讨论

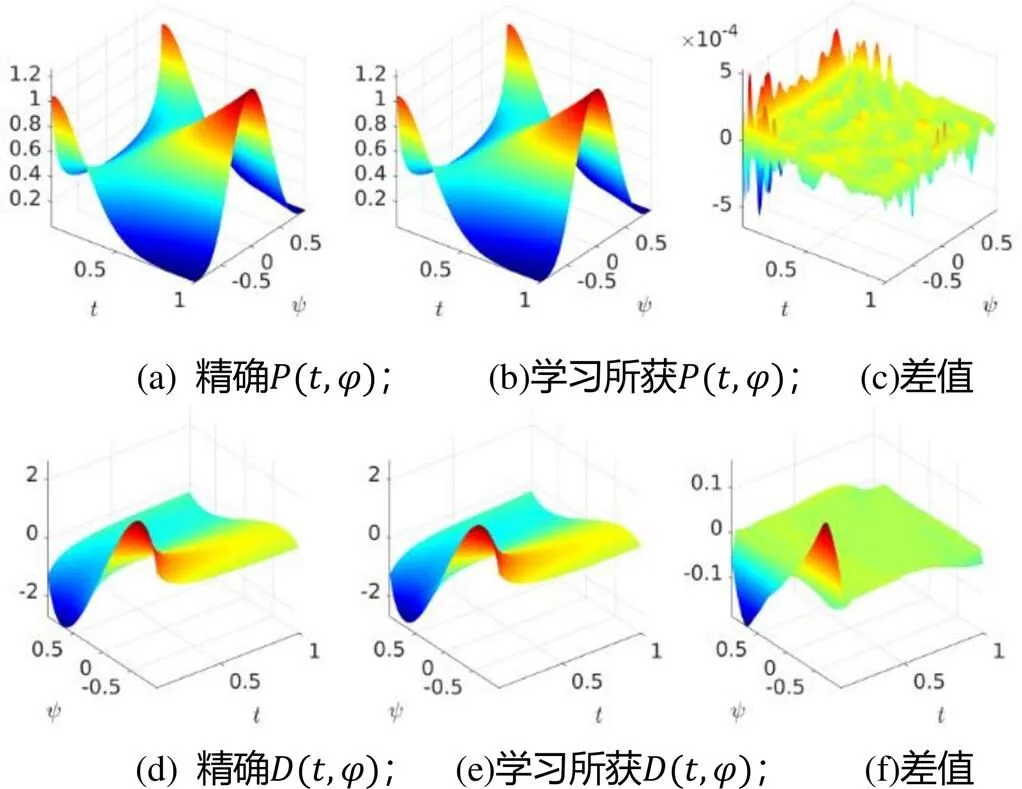
图3 第一组概率密度函数、条件期望扩散函数及其深度学习结果值的分布情况(a)为精确概率密度函数,(b)为精确概率密度函数的深度学习结果,(c)为二者的差值;(d)为条件期望扩散D,(e)为条件期望扩散D的深度学习结果,(f)为二者的差值
训练过程简述如下:测试结果是在Adam优化器[32]的105、2×105、3×105和4×105的连续时间段之后获得的,相应的学习率分别为10-3、10-4、10-5和10-6。每个时间段均对整个数据集完整计算一次。因此,Adam优化器的总迭代次数是数据个数除以最小批量值的106倍。本文使用的小批量大小是20000,数据点的数量是20000。
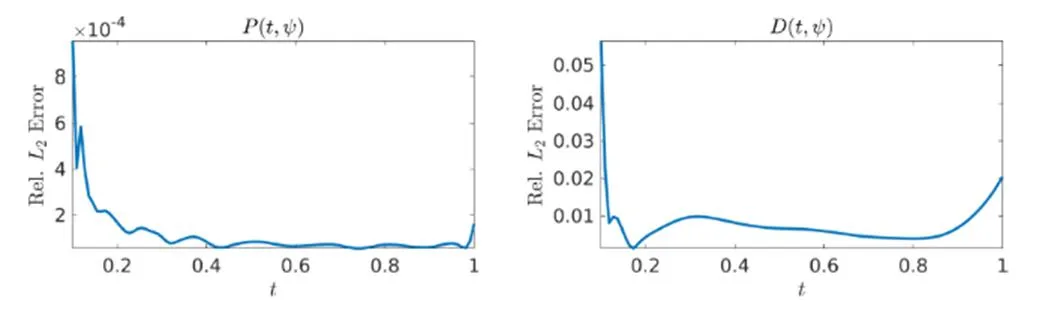
图4 条件期望扩散模型学习所得数据的误差。左图为精确概率密度函数及其深度学习结果的相对L2误差(Rel. L2 Error),右图为精确和学习的条件期望扩散D(t,) 的相对L2误差(Rel. L2 Error)
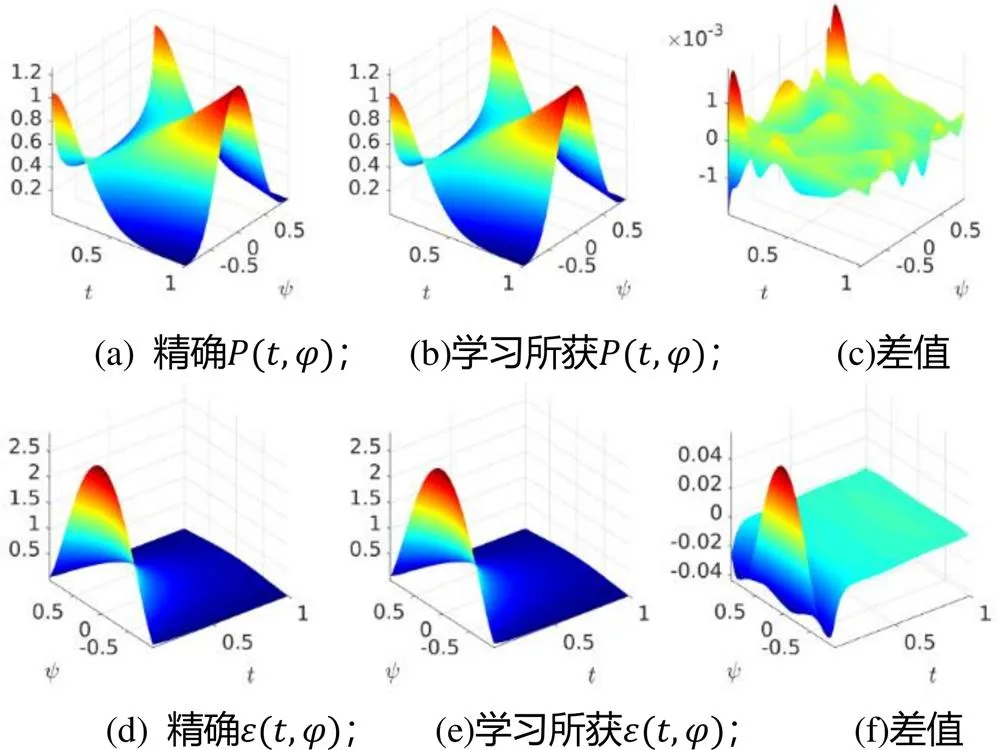
图5 第二组精确概率密度函数、条件期望耗散函数及其深度学习测试值的分布情况。(a)精确概率密度函数,(b)精确概率密度函数的深度学习结果,(c)二者的差值;(d)条件期望耗散,(e)条件期望耗散的深度学习结果,(f)二者的差值

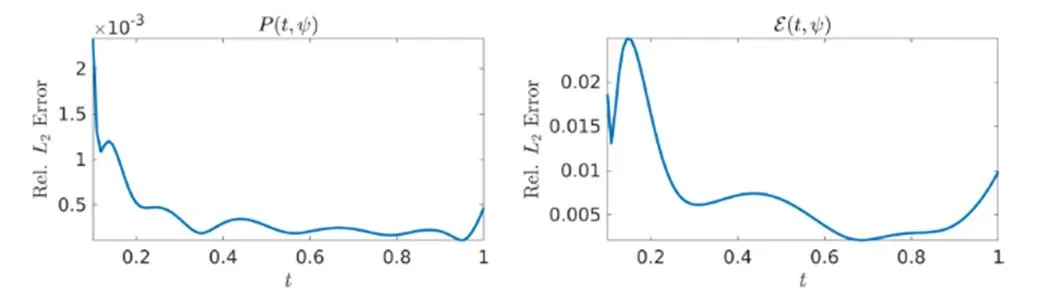
图6 条件期望耗散模型学习所得数据的误差。顶部面板中描绘了与学习函数相邻的精确概率密度函数P(t,ψ),而精确和学习的条件期望耗散E(t,ψ)绘制在底部面板中
5 结束语
本文提出了一个数据驱动的湍流标量混合非封闭项学习模型框架。在这个框架中,非闭合项是通过PDF输运方程,以及在PDF上观察到一些高保真的观测值来学习的。上述提出的框架可以直接扩展到涉及多物种混合的高维情况,避开了数值离散化的缺陷,利用数据点位于低维流形的特点设计了可扩展到高维的算法。此外,本研究中所提出方法也可以高度扩展到研究湍流时经常遇到的大数据客体,使这些数据将以更小批量、更小计算量得到有效处理。
[1]R.S. Brodkey(Ed.), Turbulence in Mixing Operation[D]. Academic Press,New York,NY,1975.
[2]S. B. Pope,Turbulent Flows[D]. Cambridge University Press,Cambridge,UK,2000.
[3]D. C. Haworth,Progress in probability density function methods for turbulent reacting flows[J]. Prog. Energ. Combust.,2010(36):168-259.
[4]A. G. Nouri,M. B. Nik,P. Givi,D. Livescu,S. B. Pope, A self-contained filtered density function[J]. Phys. Rev. Fluids,2017(2).
[5]S. S. Girimaji,Y. Zhou, Analysis and modeling of subgrid scalar mixing using numerical data[J]. Phys. Fluids,1996(8):1224-1236.
[6]F. A. Jaberi,R. S. Miller,C. K. Madnia,P. Givi,Non-Gaussian scalar statistics in homogeneous turbulence[J]. J. Fluid Mech.,1996(313):241-282.
[7]S. L. Christie,J. A. Domaradzki,Scale dependence of the statistical character of turbulent fluctuations in thermal convection[J]. Phys. Fluids,1994(6):1848-1855.
[8]A. Eckstein,P. P. Vlachos,Digital particle image velocimetry (dpiv) robust phase correlation[J]. Measurement Science and Technology,2009(20):055401.
[9]F. Pereira,M. Gharib,D. Dabiri,D. Modarress, Defocusing digital particle image velocimetry:a 3-component 3-dimensional dpiv measurement technique. application to bubbly flows[J]. Experiments in Fluids,2000(29):S078-S084.
[10]E. Weinan,J. Han,A. Jentzen,Deep learning-based numerical methods for high-dimensional parabolic partial differential equations and backward stochastic differential equations[J]. Communications in Mathematics and Statistics,2017(5):349-380.
[11]S. H. Rudy,S. L. Brunton,J. L. Proctor,J. N. Kutz, Data-driven discovery of partial differential equations[J]. Science Advances,2017(3):1602614.
[12]M. Raissi,P. Perdikaris,G. Karniadakis,Physics-informed neural networks:A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics,2018.
[13]M. Raissi, Deep hidden physics models: Deep learning of nonlinear partial differential equations[J]. Journal of Machine Learning Research,2018(19):1-24.
[14]S. Subramaniam,S. B. Pope,A mixing model for turbulent reactive flows based on Euclidean minimum spanning trees[J]. Combust. Flame,1998(115):487-514.
[15]S. B. Pope,A Model for Turbulent Mixing Based on Shadow-Position Conditioning[J]. Phys. Fluids,2013(25):110803.
[16]S. Tavoularis,S. Corrsin,Experiments in nearly homogenous turbulent shear flow with a uniform mean temperature gradient[J]. Part 1,J. Fluid Mech.,1981(104):311-347.
[17]V. Eswaran,S. B. Pope,Direct numerical simulations of the turbulent mixing of a passive scalar[J]. Phys. Fluids,1988(31):506-520.
[18]P. A. McMurtry,P. Givi,Direct numerical simulations of mixing and reaction in a nonpremixed homogeneous turbulent flow[J]. Combust. Flame,1989(77):171-185.
[19]S. L. Christie,J. A. Domaradzki,Numerical evidence for the nonuniversality of the soft/hard turbulence classification for thermal convection[J]. Phys. Fluids,1993(A 5):412-421.
[20]T. H. Solomon,J. P. Gollub,Thermal boundary layers and heat flux in turbulent convection:The role of recirculating flows[J]. Phys. Rev.,1991(A 43):6683-6693.
[21]S. T. Thoroddsen,C. W. Van Atta,Exponential tails and skewness of density-gradient probability density functions in stably stratified turbulence[J]. J. Fluid Mech.,1992(244):547-566.
[22]Jayesh,Z. Warhaft,Probability distribution of a passive scalar in grid generated turbulence[J]. Phys. Rev. Lett.,1991(67):3503-3506.
[23]Jayesh,Z. Warhaft,Probability distribution,conditional dissipation,and transport of passive temperature fluctuations in grid-generated turbulence[J]. Phys. Fluids A,1992(4):2292-2307.
[24]M. Raissi,G. E. Karniadakis, Hidden physics models: Machine learning of nonlinear partial differential equations[J]. Journal of Computational Physics,2018(357):125-141.
[25]Baydin A. G.,Pearlmutter B. A.,Radul A. A.,et al. Automatic differentiation in machine learning:A survey[J]. Journal of Machine Learning Research,2018,18(153):1-43.
[26]M. Abadi,A. Agarwal,P. Barham,et al.,Tensor flow: Large-scale machine learning on heterogeneous distributed systems[J]. arXiv:2016,1603(04467).
[27]R.H.Kraichnan,Closures for probability distributions[J]. Bull. Amer. Phys. Soc.,1989(34):2298.
[28]H.Chen,S.Chen,R.H. Kraichnan,Probability distribution of a stochastically advected scalar field[J]. Phys. Rev. Lett.,1989(63):2657-2660.
[29]S. B. Pope,Mapping closures for turbulent mixing and reaction[J]. Theor. Comp. Fluid Dyn.,1991(2):255-270.
[30]R. S. Miller,S. H. Frankel,C. K. Madnia,P. Givi, Johnson-Edgeworth translation for probability modeling of binary scalar mixing in turbulent flows[J]. Combust. Sci. Technol.,1993(91):21-52.
[31]P. Ramachandran,B. Zoph,Q. V. Le, Searching for activation functions[J]. arXiv:2017,1603(04467).
[32]D. P. Kingma,J. Ba,Adam: A method for stochastic optimization[J]. arXiv:2014,1412(6980).

