圆形蜂窝的异面冲击性能研究
孙玉瑾,孙德强,安 兴,焦思涵
(陕西科技大学 轻工科学与工程学院 中国轻工业功能印刷与运输包装重点实验室3S包装新科技研究所 轻化工程国家级实验教学示范中心 陕西省造纸技术与特种纸品开发重点实验室,陕西 西安 710021)
0 引言
蜂窝结构作为一种轻量化结构,具有优异的吸能特性,在先进航空航天零部件、包装材料、军事装备、车辆零部件等领域有着重要的应用[1-3].蜂窝的共面力学行为,包括坍塌模式、压缩强度、能量吸收能力等,蜂窝相对密度、蜂窝壁角度、蜂窝壁厚和冲击速度对六边形蜂窝变形模式和力学性能的影响已经得到了广泛的研究[4-7].在共面压缩条件下,圆形蜂窝比相对密度相同的六边形蜂窝吸收更多的能量.作为夹芯部分,蜂窝的异面力学性能相比共面,表现出更高的比刚度和更好的比能量吸收特点[8].因此,研究圆蜂窝结构异面动态力学行为和能量吸收特性,是十分必要的.
多层排列的圆形蜂窝作为二维轻质蜂窝材料,其弹性变形、塑性破坏和能量吸收特性得到了广泛研究.例如,Sun等[9]给出了多层规则排列圆形蜂窝共面变形模式的临界转换速度、动态致密化应变和动态峰应力的经验公式,并采用简化的能量吸收模型对其能量吸收性能进行了评价;Hu等[10]分别采用理论和数值方法研究了规则和交错排列圆形蜂窝的动态异面冲击性能,两者结果具有较好的一致性.已有研究表明,结构参数和冲击速度影响着二维蜂窝的动态性能[11-14];此外,D′Mello等[15]采用试验方法研究了不同速度下圆形聚碳酸酯蜂窝的异面动力学破碎响应;付春英等[16]比较了规则排列和交错排列圆形蜂窝共面动态冲击力学性能,得出了两种排列方式的变形模式;何强等[17]建立了具有固定相对密度的含随机固体填充孔的蜂窝结构的有限元模型,研究了不同孔洞填充比和冲击速度对圆形蜂窝变形模式和吸能特性的影响,得到在高速冲击下含固体填充孔的蜂窝结构比能量吸收高于规则排列的蜂窝结构.
从上述分析可以看出,蜂窝结构受到异面冲击载荷时,缺少对其能量吸收特性的研究.本文在此基础上,建立了基于阵列的圆形蜂窝显示动力学有限元计算模型,在研究其受异面冲击时的变形模式基础上,重点分析了壁厚、排列方式和冲击速度对其能量吸收特性的影响.
1 圆形蜂窝结构的计算模型
1.1 圆形蜂窝结构
圆形蜂窝由相邻几个空心薄壁圆筒相切组成,如图1所示.常用的圆形蜂窝有两种排列方式:其一,为规则排列,如图1(a)所示,每一个圆筒与周围4个圆筒相切;其二,为交错排列,如图1(b)所示,每一个圆筒与周围6个圆筒相切.图中参数t为壁厚,R为半径,h为蜂窝深度.异面方向指垂直于x-z平面的每个圆筒的轴线方向,即y轴方向.

图1 图形蜂窝结构示意图
假设基材密度为ρs,圆形蜂窝的密度为ρ*,两者比值ρ*/ρs即为蜂窝结构的相对密度Δρ.根据圆形蜂窝结构的构型特征,以图2中框线部分计算相对密度.假设规则排列和交错排列圆形蜂窝的相对密度分别为ΔρR和Δρc,则:

图2 圆形蜂窝相对密度计算示意图

1.2 有限元模型
采用显式动力学软件ANSYS/LS-DYNA 建立圆形蜂窝异面冲击分析的有限元模型,具体的异面冲击计算模型如图3所示.将圆形蜂窝样品置于两刚性压板之间,上压板有足够大的质量,以恒定的速度v向下移动,保证试样绝对塌陷.蜂窝初始深度h=15 mm,基体材料为双线性应变硬化模型,一典型材料为铝合金,其参数如表1所示.对蜂窝体采用五个积分点的Shell163壳单元进行网格划分,剪切因子为5/6,定义整个模型为单面自动接触,蜂窝体与上下刚性压板之间设为自动面面接触,摩擦系数设为0.02.
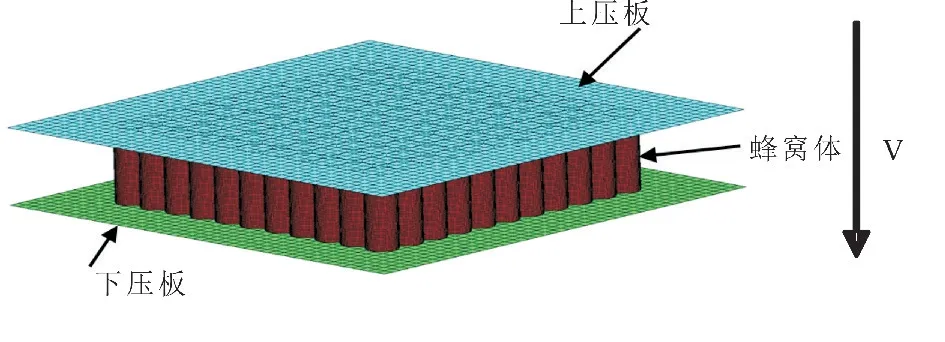
图3 圆形蜂窝阵列的异面冲击有限元模型

表1 圆形蜂窝基体材料的参数
1.3 模型的可靠性分析
Hu等[10]通过动量守恒推导出圆形蜂窝结构在冲击速度v下的平台应力σ,可采用式(3)进行:

式(4)中:C1—固定常数;n1—固定常数;σys—蜂窝基材的屈服应力.
为了验证有限元计算模型的可靠性,建立规则排列圆形蜂窝结构,其参数设置(v=10 m/s,t=0.018 mm,R=1.5 mm)与Hu等一致,得到准静态压缩载荷作用下结构的应力-应变曲线,如图4所示,应力σ为刚性上压板作用在蜂窝芯材上的压缩力F与蜂窝体受力面积A的比值;应变ε=l/h,l为异面方向刚性压板的压缩位移.图4 给出了Hu等的平台应力理论计算值.
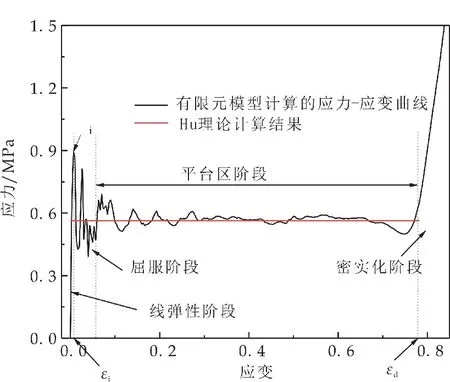
图4 准静态载荷下规则圆形蜂窝结构的应力应变曲线
从图4的应力-应变曲线来看,应力随应变的变化过程分为四个阶段:(1)线弹性阶段,在此阶段,应变很小,但应力急剧增加到局部最高点,称为初始蜂应力σi,对应的应变称为初始应变εi;(2)到达初始峰应力后,应力快速下降并呈现较大波动,这一阶段称为屈服阶段;(3)随着应变的增加,应力趋于平稳,并在小范围内波动,此阶段称为平台区阶段;(4)当应变进一步增加至某一值时,应力快速增加,从而使得曲线进入密实化阶段,此时的应变称为密实化应变,记为εd.
该应力-应变曲线与Hu 文中的曲线变化一致,而且平台区阶段的应力与Hu的理论计算值吻合较好,充分证明该计算模型的可靠性.
为了消除尺寸效应对模型的影响,本文创建了5×7、7×7、8×9、9×11、10×11、11×11、11×12、13×15、16×16、21×21共10种不同单元数目的交错排列圆形蜂窝有限元模型进行运算,通过比较得到,单元数目为35 的5×7 阵列与单元数目为441的21×21 阵列的平台区应力变化差距为4.5%,而单元数目为121的11×11阵列与其差距仅0.4%,因此为计算精确并节约时间成本,本文选用11×11的阵列.同时,为了保证计算模型的计算精度,计算结果表明当单元边长小于0.30 mm时,其关键的力学参数平台应力趋于稳定,因此采用0.25 mm 作为有限元模型的单元边长.
2 计算结果与分析
本文采用的圆形蜂窝结构参数为:R=3 mm,h=15 mm,t=0.02~0.06 mm,v有3 m/s、50 m/s和100 m/s三种,从而研究冲击速度和壁厚对圆形蜂窝结构异面冲击性能的影响规律.
2.1 变形模式及应力-应变曲线
图5给出t=0.06 mm 的交错排列圆形蜂窝在不同冲击速度下的变形模式.从变形过程来看,低速(v=3 m/s)冲击时,冲击端首先发生微小屈曲变形,随后在固定端产生较大局部变形;当应变达到0.2时,固定端的变形明显大于冲击端变形.而且,随后随压缩位移的增加,变形均集中到固定端,冲击端变形较小,直至蜂窝被压实.当冲击速度增加到50 m/s时,蜂窝变形首先发生在冲击端,随后固定端才发生变形;当应变为0.2时,可见冲击端变形明显大于固定端;但是当应变达0.4时,上下两端的变形程度几乎相同,且随着位移的增加,两端的变形同时增加,直至被压实.冲击速度达到高速100 m/s时,惯性效应增加,变形首先发生在冲击端,并且变形持续增加,固定端变形量较小;当应变达到0.4时,固定端才有明显变形,之后变形仍以冲击端为主,直至蜂窝被压实.此外发现,规则排列圆形蜂窝在不同冲击速度下也发生类似的变形模式.由此可见,圆形蜂窝受到不同速度冲击时,其变形模式各不相同.

图5 不同冲击速度下交错排列圆形蜂窝的变形模式
图6给出了交错排列圆形蜂窝结构的应力-应变曲线.从图中可以看出,在不同冲击速度下,其应力-应变曲线也表现不同.当v=3 m/s时,初始峰应力较小,平台区应力基本恒定,变化较小,直到应变为0.75 左右时,应力急剧增加,蜂窝发生密实化.当v=50 m/s时,初始峰应力大幅度增加,平台区应力明显高于低速时的平台应力,但在一定范围内出现波动.当v=100 m/s时,初始峰应力进一步增大,平台区应力增加明显,且发生较大幅度波动,直至发生密实化.由此可见,冲击速度对圆形蜂窝结构异面性能的影响较大,速度增加使初始峰应力增加,平台区应力得到提高,密实化应变也发生延迟.

图6 不同冲击速度下交错排列圆形蜂窝的应力应变曲线(R=3 mm,t=0.06 mm)
2.2 圆形蜂窝结构的平台应力分析
平台应力(σ)是描述二维多孔材料或结构能量吸收特性的重要指标.平台应力越大,其能量吸收能力越强.将其定义为试样从平台区到密实化发生时的应力平均值,其计算公式[18]为:

式(5)中:εi—初始峰应力(MPa),σi—初始应变;εd—密实化应变.εd指发生密实化开始时的应变,是评价材料或结构吸能特性的重要参数.本文利用能量吸收效率法[19]来确定,即能量吸收效率取得最大值时所对应的应变.
在此,能量吸收效率Eea为:
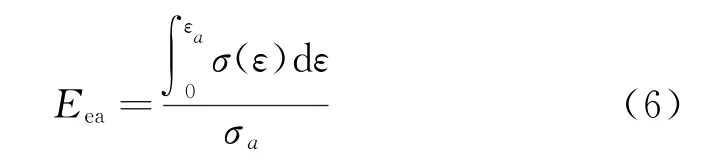
式(6)中:εa—应力-应变曲线中的任一应变,σa—εa对应的应力(MPa).由下式可得到密实化应变εd为:

图7为交错排列圆形蜂窝一典型的应力-应变曲线及其对应的能量吸收效率-应变曲线.由图可知,能量吸收效率最大值对应的应变即为密实化应变εd,此时的开始应力快速上升引起了能量吸收效率开始下降.
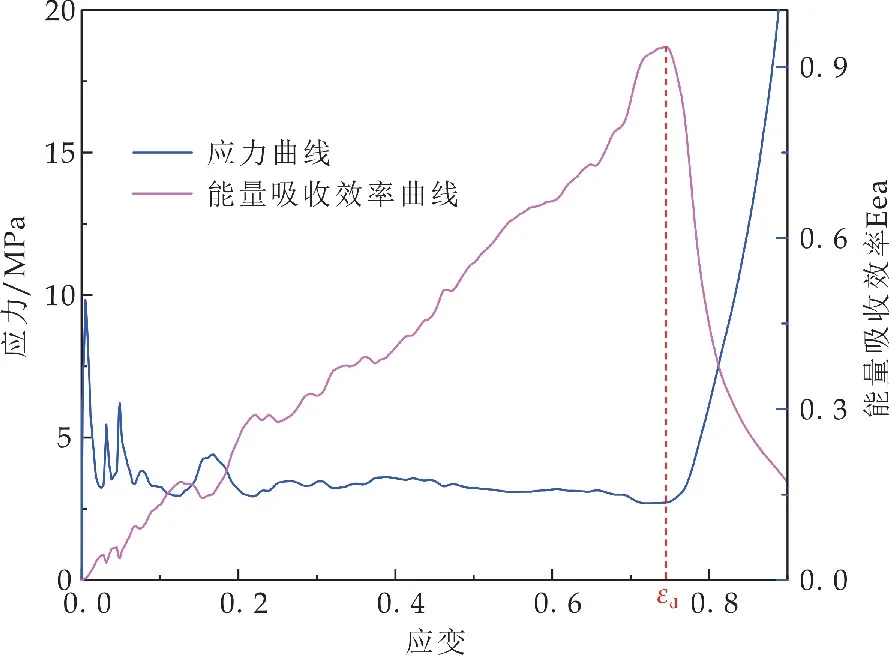
图7 应力-应变曲线及能量吸收效率曲线(t=0.06 mm,R=3 mm,v=50 m/s)
表2给出了两种排列方式的圆形蜂窝在不同壁厚和冲击速度下的平台应力.从表中数据可以看出,在同一冲击速度下,其余结构参数一定时,平台应力随着壁厚的增加而增加,这符合公式(3)的变化规律;而且当结构参数和冲击速度一定时,交错排列圆形蜂窝的平台应力均高于规则排列.
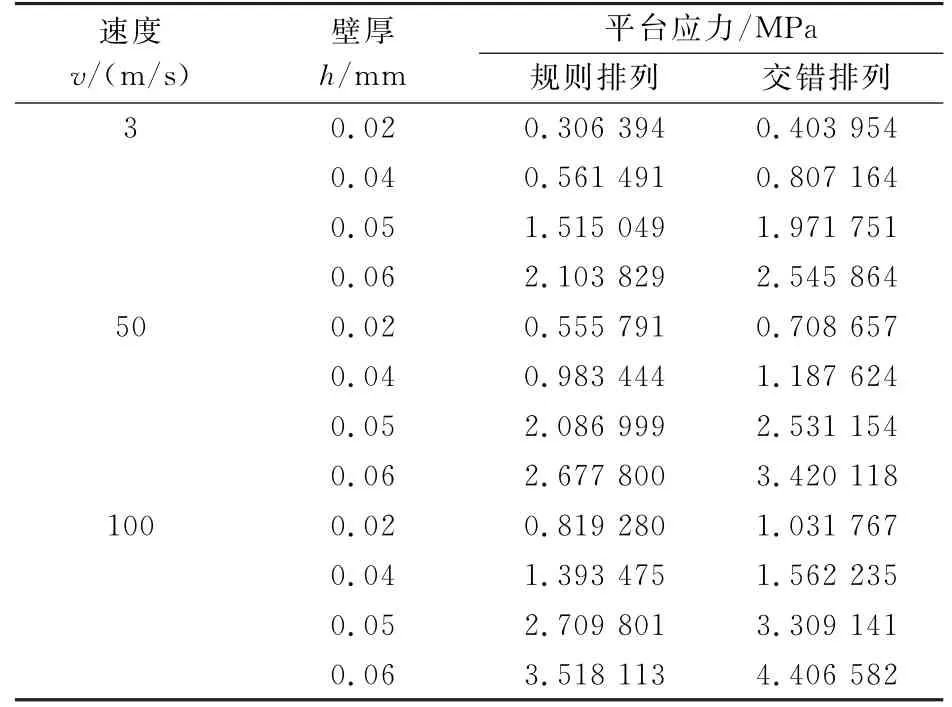
表2 圆形蜂窝的平台应力值
为了定量比较这种增强,图8通过数据拟合描述了交错排列和规则排列圆形蜂窝在低、中、高三种冲击速度和四种壁厚情况下的平台应力.结果表明交错排列圆形蜂窝的平台应力是规则排列的1.23倍左右,表明交错排列圆形蜂窝的承载能力比规则排列圆形蜂窝的高.
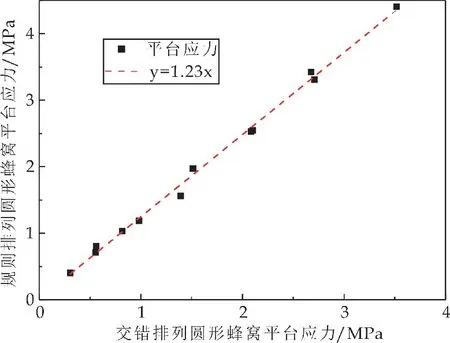
图8 规则排列和交错排列圆形蜂窝平台应力比较
2.3 圆形蜂窝的能量吸收特性
多孔材料结构比能量吸收是评价其能量吸收能力的另一个重要指标,定义[14]为:

式(8)中:E—结构材料单位体积能量吸收(J/cm3),即应力-应变曲线所围的积分面积.曲线中任一应变下的单位体积能量吸收[14]为:
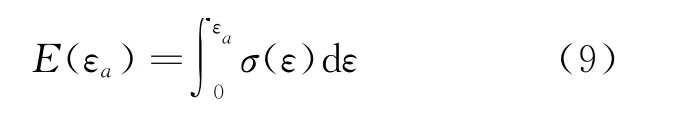
式(9)中:εa—应力-应变曲线中任一应变,且0<εa≤εd.
从任一应变下的比能量吸收比率η,可以了解材料结构在不同应变下的能量吸收变化特点,从而能够更好的控制材料结构的能量吸收能力,其计算公式如下:

图9给出了t=0.06 mm 时,两种排列方式的圆形蜂窝在不同冲击速度下的单位质量能量吸收图.由图可以看出,圆形蜂窝单位质量能量吸收随速度的增加而增加,而且在密实化应变(εd为0.75左右)之前,与应变呈近似线性增长.在相同结构参数下,交错排列的比能量吸收要高于规则排列的.当应变小于0.2时,二者差距较小,当应变大于0.2时,二者的差距逐渐变大,密实化应变之后差距再次缩小.当v=3 m/s时,交错排列圆形蜂窝比规则排列的比能量吸收高5%,而当v=50和100 m/s时,二者相差10%和8%.由此可见,在动态冲击条件下,交错排列圆形蜂窝的比能量吸收要高于规则排列的,而且随着冲击速度的增大二者的差距会进一步增加.

图9 不同冲击速度下圆形蜂窝结构的比能量吸收(R=3 mm,t=0.06 mm)
图10给出了交错排列下两种壁厚的圆形蜂窝在不同冲击速度下的比能量吸收与应变的关系图.从图10可以看出,随着壁厚的增加,比能量吸收也在增加,但同时也受到冲击速度的影响,很难确定哪一个因素影响更明显.此时可以通过比能量吸收比率进一步研究圆形蜂窝结构的能量吸收特性,图11给出了交错排列下两种壁厚的圆形蜂窝在不同冲击速度下的比能量吸收比率与应变的关系图.

图10 交错排列圆形蜂窝结构比能量吸收(R=3 mm)
从图11可以看出,壁厚和冲击速度的增加均使不同应变下比能量吸收比率得到提高.当ε=0.2时,t=0.02 mm 的圆形蜂窝在v=3 m/s、50 m/s和100 m/s的冲击下的比能量吸收比率分别是36%、43%和47%,明显高于t=0.06 mm时的26%、29%和32%.但是当应变从0.2变化到0.4时,t=0.06 mm的比能量吸收的比率增长迅速,三种速度下最大增幅为25%,此时t=0.02 mm 的最大增幅仅为12%.随后的应变中,两者比能量吸收的比率增幅相差不大.当ε=0.7时,两种壁厚的比能量吸收比率在同一冲击速度下几乎无差别.另外,冲击速度的变化对相同壁厚的圆形蜂窝比能量吸收比率影响规律类似.分析表明,比能量吸收比率主要取决于应变的大小,因此可以通过调整不同应变下的能量吸收比率,从而有效的控制材料结构的吸能特性,这可为不同应用条件下缓冲吸能结构的设计提供一定的参考价值.

图11 交错排列圆形蜂窝的比能量吸收比率(R=3 mm)
3 结论
本文建立了两种排列方式的圆形蜂窝结构受到异面冲击的有限元模型,并验证其可靠性.通过分析它们的变形模式、平台应力和能量吸收能力,得到圆形蜂窝结构异面力学性能如下:
(1)圆形蜂窝受到不同速度的异面冲击时,表现出不同的变形模式.受惯性效应的影响,低速时,变形集中于固定端;中速时,冲击端和固定端变形均衡;高速时,变形集中于冲击端.
(2)圆形蜂窝的平台应力受冲击速度和壁厚的影响.在结构参数固定时,平台应力随着冲击速度增加而增加;在同一冲击速度下,平台应力随着壁厚的增加而增大;冲击速度和参数相同时,交错排列圆形蜂窝的平台应力要高于规则排列的.
(3)圆形蜂窝比能量吸收同样受冲击速度和壁厚的影响,且随二者的增大而增大.变形应变不同,圆形蜂窝能量吸收比率不同.应变较小时,小壁厚蜂窝结构的能量吸收效率高于大壁厚,但是随着应变的增加大壁厚蜂窝结构的能量吸收比率增长迅速,发生密实化应变时,二者能量吸收比率相差最小.

