Adaptive fuzzy terminal sliding mode control for the free-floating space manipulator with free-swinging joint failure

Qingxuan JIA, Bonan YUAN, Gang CHEN, Yingzhuo FU

School of Automation, Beijing University of Posts and Telecommunications, Beijing 100876, China

KEYWORDS Space manipulator;Free-swinging joint failure;Sliding mode control;Adaptive fuzzy control;Robust controllers

Abstract Space manipulator with free-swinging joint failure simultaneously contains kinematic and dynamic coupling relationships, so it belongs to a new underactuated system. To allow the manipulator to carry on tasks, an effective robust underactuated control method for the space manipulator with free-swinging joint failure is studied in this paper.Considering the effect of model uncertainty and joint torque disturbance,a robust underactuated control system based on the Terminal Sliding Mode Controller(TSMC)is designed,but two drawbacks are discussed:(A)Robustness depraves with eliminating chattering. (B) Control parameters are difficult to be determined under unknown uncertainty and disturbance.To improve the TSMC,the adaptive fuzzy controller is introduced to estimate the real effect of unknown uncertainty and disturbance according to deviations of sliding mode and its reaching law.The estimated result is directly compensated into active joints torque.In simulation,the space manipulator with free-swinging joint executes tasks based on the TSMC and the Adaptive Fuzzy Terminal Sliding Mode Controller (AFTSMC) respectively.Same tasks can be finished with smaller joints torque and stronger robustness based on the AFTSMC. Therefore, AFTSMC can serve as an effective robust control method for the space manipulator with free-swinging joint failure under unknown model uncertainty and torque disturbance.

1. Introduction

With strong flexibility and outstanding working performance,the space manipulator is widely utilized to perform various onorbit tasks,such as space station assembling,spacecraft capturing and releasing,EVA supporting,etc.To coordinate with space station long-term service, the space manipulator is required to work reliably more than a decade. As the basic actuator of space manipulator, the joint is a complex electromechanical system consisting of many parts. Abnormal operation of any parts will cause joint failure. However,space manipulator usually executes many burdensome tasks, like carrying large load whose mass reaches up to 8–25 tons,which makes joint parts always work in ultimate conditions,and suffer from severe abrasion, so that joint is prone to fail in longterm service.Subjected to hazardous space environment,repairing the fault joint on-orbit unavoidably relies on human astronaut extra-vehicular activity,which causes high costs and risks in maintenance procedure. Thus many researchers try to study effective failure treatment strategies to keep using the space manipulator with joint failure.

According to the failure experience of Canadarm1 on US space shuttle,Wu et al.divided joint failure of space manipulator into two types:Fail-on and fail-off,explicitly corresponding to subsequent Locked joint failure and Free-swinging joint failure.Locked joint failure means the joint is rigidly locked as long as the abnormal operation is detected, and it makes the space manipulator lose some Degrees of Freedom (DOFs)and turn into a new manipulator.Reconfiguring the kinematic and dynamic model, we can keep using the space manipulator with locked joint failure. Free-swinging joint can’t support torque anymore, so it freely swings like a frictionless hinge.Free-swinging joint failure may be caused by motor excitation losing, gear engagement separating, or transmission shaft cracking in frequently alternant speed-up and speed-down.It makes the manipulator working performance seriously degrade, especially losing operation force on End-Effector(EEF). And kinematic and dynamic characteristics of the whole system become more complicated.

Researches on locked joint failure treatment are abundant.However,there is still lacking in an effective treatment strategy for free-swinging joint failure.For the space manipulator with free-swinging joint failure, its DOFs are more than effective actuators,so it belongs to an underactuated multibody system.According to working experiments of the underactuated manipulator on the ground,passive joint regulation is the typical task,so researchers designed many types of underactuated controllers based on dynamic coupling between healthy joints and free-swinging joints.But for the space manipulator with free-swinging joint failure,motions among healthy joints,freeswinging joints,free-floating base,EEF are strongly coupled in the meantime. Because of lacking effective actuation units,free-swinging joints, base, EEF can only be passively driven by healthy joints,so they are usually called as‘‘controlled units”. Particularly, we call free-swinging joints as passive joints and healthy joints as active joints. We need to decouple the complicated coupling motion inside the system to establish the dynamic model for the space manipulator with freeswinging joint failure. Then, an underactuated controller can be further designed.

First of all, we analyse the dynamic characteristics of the space manipulator with free-swinging joint failure, to obtain the analytical mapping relations from healthy joints torque to controlled units acceleration.Relevant researches have been carried out mainly aiming at dynamic modelling of the underatucated manipulator on the ground. Arai et al.derived the unintegrable acceleration mapping relationship between active joints and the third passive joint for a 3-DOF planar underatucated manipulator.It was called as the dynamic coupling relationship which belongs to the second-order non-holonomic constraint of state variables. Lai et al. discussed the dynamic coupling inside 2-DOF,3-DOF,4-DOF,and n-DOFplanar underatucated manipulators with single free-swinging joint, and pointed out only if the first joint freely swings, can the dynamic coupling between active joints and the passive joint be integrated into the kinematic one.However,researches above used too many geometric constraints of planar mechanism to simplify analysis procedure. For the high-DOF space manipulator with any number of free-swinging joints,Mukherjee and Chenestablished the dynamic model through Lagrange equation,and derived dynamic coupling relationship between active joints and passive joints based on Hamiltonian operator. Chen et al.discussed the dynamic coupling relationship between adjacent active joint and passive joint for the space manipulator. Lidefined the dynamic coupling degree to describe the ability of active joints regulating passive joints. However,researches above aimed at the space manipulator installed on the large spacecraft which can be regarded as the fixed base, so they couldn’t thoroughly decouple the complicated motion coupling inside the free-floating manipulator system. Fortunately, authors have analysed kinematic and dynamic characteristics of the free-floating space manipulator with free-swinging joint failure. And kinematic and dynamic coupling relationships between active joints and all controlled units have been definitely given in Ref.19 for the first time.Thereinto, the dynamic coupling relationship is the basis for underactuated controller design.

Surrounding underatucated manipulators ignoring gravity effect,many underatucated control schemes have been proposed.Shin and Leeestablished the EEF dynamic equation of the underatucated chain system,and designed PD controller to control EEF to track the predefined trajectory. Maciel et al.put forward joint torque calculation method based on PD control for a n-DOF underatucated manipulator. Considering viscous friction in the free-swinging joint,Chen et al.utilized the adjacent healthy joint to regulate the fault joint based on PD control method. According to the knowledge of robot control, PD controller is only effective without model uncertainty and external disturbance. However, the changeful state of free-swinging joint makes it difficult to acquire the accurate model parameters of the manipulator. Moreover, active joints usually suffer from external torque disturbance caused by abrasion, deformation,or vibration, which directly acts on the control input.Model uncertainty and torque disturbance exacerbate the dynamic characteristics of system,so we need to design the underatucated controller which is robust to uncertainty and disturbance.

Sliding mode control method possesses natural robustness.It makes the controlled variables converge in two stages.In the first stage, a compensation term‘‘covers” uncertainty and disturbance effect to make controlled variables converge to the‘‘Zero Sliding Mode Manifold”.The second stage has the natural invariance to uncertainty and disturbance,and controlled variables‘‘slide”to desired states along the sliding mode manifold. Many controllers have been designed based on sliding mode control method for the underatucated manipulator.Henmi et al.designed a sub-controller for passive joints based on conventional sliding mode control method, and the global stability is guaranteed. Aiming at the case that passive joints are more than active joints, Bergerman and Xuintegrated a stepwise strategy into sliding mode controller to regulate all joints to desired angles in several steps. However, the discontinuous switching in the vicinity of sliding mode manifold brings about ‘‘Chattering” phenomenon, which introduces high-frequency oscillation into controlled variables motions. Chattering threatens stability and safety of the system. To inhibit chattering, sliding mode control method is improved by adding high-order sliding mode manifold.With order increasing, the oscillation amplitude decreases.However, the high-order sliding mode controller can’t absolutely eliminate chattering, and the controller is more complicated with higher order. To eliminate chattering, some researchers proposed many methods to make the switching process equivalently continuous, but it will impair control robustness in the vicinity of the sliding mode manifold. There exists contradiction between chattering elimination and strong robustness. Meanwhile, the fact that model uncertainty and torque disturbance are usually unknown makes it difficult to select the reasonable control parameter to enable sliding mode controller perfectly cover uncertainty and disturbance effect.Moreover,because of dynamic coupling,the free-floating base drifts with manipulator motion. Large base deflection influences communication and energy collection efficiency, and makes the whole system unstable.Therefore,we need to design an underactuated controller, which is reliably robust to unknown model uncertainty and torque disturbance, to control space manipulator with free-swinging joint failure to execute tasks and limit base deflection at the same time.

In this paper, we study the underactuated control scheme which is reliably robust to unknown model uncertainty and torque disturbance for the space manipulator with freeswinging joint failure.First of all,we discuss the dynamic coupling inside the system, and derive mapping relationships between active joints acceleration/torque and controlled units acceleration.With the help of robustness of sliding mode control method, we design the Terminal Sliding Mode Controller(TSMC) which makes controlled variables converge in finite time.Particularly,we discuss control parameter selection difficulty with unknown model uncertainty and joints torque disturbance, and robustness degradation for eliminating chattering with continuously switching to sliding mode manifold. In fact, two problems above both due to the robustness of sliding mode controller are exceedingly dependent on a certain control parameter selection. To improve the TSMC, we further integrate the adaptive fuzzy controller. Fuzzy controller utilizes human prior knowledge to estimate the real effect of model uncertainty and torque disturbance according to current controlled variables states. The estimation result is further substituted into joints torque calculation to actively compensate uncertainty and disturbance effect. In this way,the decisive effect of control parameter on robustness can be reduced for the most part. To improve fuzzy estimation accuracy, the fuzzy control parameters are adaptively adjusted according to real-time compensation results. The Adaptive Fuzzy Sliding Mode Controller (AFTSMC) that is strongly robust to model uncertainty and torque disturbance is acquired for the space manipulator with free-swinging joint failure.The effectiveness of the AFTSMC is verified in simulation. The traits of this paper mainly include:

(1) We proposed an effective robust underactuated control method for a new underactuated multibody system,the space manipulator with free-swinging joint failure,for the first time, to enable the space manipulator to keep executing on-orbit tasks.

(2) After integrating adaptive fuzzy controller, the effect of unknown model uncertainty and torque disturbance is actively estimated and compensated, so the robustness of TSMC is not strictly dependent on parameter selection. Control parameter selection difficulty and robustness degradation for eliminating chattering can be effectively avoided.

(3) Through adaptively adjusting fuzzy control parameters,the estimation result will be close to the real effect of uncertainty and disturbance as much as possible,so that active joints can accurately compensate uncertainty and disturbance with smaller torque.

The remaining paper is organized as follow: In Section 2,we derive dynamic coupling relationships between active joints and passive joints, base, EEF, respectively. The TSMC is designed based on the dynamic coupling in Section 3.Particularly, we discuss the control parameter selection difficulty under unknown model disturbance and torque disturbance,and show the robustness degradation with continuous switching to the sliding mode manifold to eliminate chattering. We further introduce the AFTSMC in Section 4, and its stability and robustness are proved. In Section 5, we give simulation experiments for some typical tasks with two kinds of controller. With comparing task results, the strong robustness of the AFTSMC to unknown model disturbance and torque disturbance is verified. Conclusion is in Section 6.

2. Dynamic coupling of the free-floating space manipulator with free-swinging joint failure

Underactuated controller design should be based on dynamic modelling of the underactuated manipulator. Therefore, we establish the dynamic model of the free-floating space manipulator with free-swinging joint failure in this section,to obtain analytical mapping relationships between active joints acceleration/torque to passive joints, free-floating base, EEF accelerations, which are defined as dynamic coupling.

2.1. Lagrange dynamic equation of the space manipulator with free-swinging joint failure

n-DOF space manipulator with free-swinging joint failure that we study is in Fig. 1. In this paper, vectors and matrixes with subscript in the upper left corner are with respect to the corresponding coordinate frame,and others with no subscript in the upper left corner are with respect to the inertial coordinate frame. Definitions of frequently-used variables are as follow

Fig. 1 Kinematic model of the n-DOF space manipulator with free-swinging joint failure.

where K is system kinetic energy, and e is system potential energy. Space manipulator is free from gravity, and we consider joints or links as rigid, so e=0. Lagrange function only contains total kinetic energy of the free-floating space manipulator system

2.2. Dynamic coupling between active joints and different controlled units

Dynamic coupling relationships can be derived from Eqs.(6)–(8).

2.2.1.Dynamic coupling between active joints and passive joints,free-floating base

2.2.2. Dynamic coupling between active joints and EEF

EEF acceleration doesn’t exist in Lagrange dynamic Eq.(4),so we can’t directly obtain dynamic coupling between active joints and EEF. When the manipulator isn’t in singularity,Eq. (A9) in Appendix A.1 is differentiable, so we have

Eq. (19) provides dynamic model for controller design for current task. After determining control law of ¨θ, the inverse solution of active joints torque can be obtained

Torque calculated from Eq. (20) is directly allocated to active joints. If the dynamic model of joint is precise, outputting torque in Eq. (20) can regulate active joints to desired angles states accurately. In this paper, we mainly study the space manipulator system control method instead of the joint control problem,so we don’t consider joint model uncertainty.

3. Terminal sliding mode controller

In practice, we can’t acquire accurate model of the space manipulator with free-swinging joint failure,and joints usually suffer from torque disturbance because of friction, flexible vibration, abrasion, and so on. We design a robust controller based on the terminal sliding mode control for the space manipulator with free-swinging joint failure, to ensure that space tasks can be completed with model uncertainty and joint torque disturbance. Then, we analyse stability and robustness of the controller, and discuss control method defects.

3.1. General control law for the free-floating space manipulator with free-swinging joint failure

Sliding model control method is primarily proposed by Emelyanov and Fedotova,and it is developed and applied in MIMO system and non-linear system by Utkin.Sliding mode controller makes controlled variables converge in two stages.Controlled variables converge to the sliding mode manifold in the first stage.In the second stage,controlled variables‘‘slide” to desired states along the sliding mode manifold. We design control laws for these two stages, respectively.

Based on Lasalle maximum invariance principle,the control system is globally stable, when V（x）<0 for s≠0, and ˙V（x）=0 only for s=0.Therefore, the sliding mode manifold corresponds to the maximum invariant set for controlled variables. To satisfy Eq. (23), we choose the exponential reaching law,which makes controlled variables converge to the sliding mode manifold in finite time.

However,sgn（S）causes the discontinuous switching to the sliding mode manifold,and time-delay of the large inertia system and discrete control process make it impossible for controlled variables to switch to sliding mode manifold in time.In subsequent control cycles,controlled variables swing in the vicinity of the manifold. This phenomenon is called as‘‘Chattering” phenomenon of the sliding mode controller. It causes high-frequency oscillation of controlled units acceleration and joint torque, which severely threatens safety and stability of the whole system. To eliminate chattering, we replace the sign function with a new saturation function containing sinusoidal function transition to obtain the continuous reaching law ˙s=-ηsat（s）-ks, where

Fig. 2 Convergence time surface to sliding mode manifold.

where bis a boundary layer of the sliding mode manifold.When |S|≤b, the continuous switching process starts, and the chattering can be eliminated thoroughly.

However,the introduction of a saturation function into the reaching law will weaken the robustness in the first convergence stage. Assuming controlled variables have been arrived at the sliding mode manifold, but model uncertainty and torque disturbance make controlled variables deviate from the manifold with speed ˙S>0,for ΔT →0,it will bring about deviation S→0≠0 in the next control period.Then,there will appear corrected speed ˙S=-η. If η> ˙S, the discontinues reaching law in Eq. (26) can rapidly subdue controlled variable into the sliding mode manifold regardless of uncertainty and disturbance. Therefore, the sliding mode controller with the discontinuous reaching law has strong robustness.The compensation item ηsgn（s） can ‘‘cover” the effect of uncertainty and disturbance.

3.2. Analysis on stability and robustness of TSMC

Then,we should substitute the reaching law and terminal sliding mode manifold into dynamic coupling to calculate active joints torque,to serve as the control input u=τto make controlled variables converge. Eq. (33) can be expressed as

Fig. 3 Convergence time curves of controlled variables ‘‘sliding” to desired values.

Fig. 4 TSMC scheme.

We obtain the TSMC for the space manipulator with freeswinging joint failure with model uncertainty and torque disturbance shown in Fig. 4.

The stability and robustness of two convergence stages need to be discussed.

3.2.1. Stability for controlled variables converging to the sliding mode manifold

Substituting Eqs. (43) and (44) into Eq. (41), we have

˙V（T）=0 only for S=0, so the TSMC is asymptotically stable.

However, in practical application, the effect of model uncertainty and torque disturbance is random and unknown,so we can’t find the analytic expression of din Eq. (40),and the accurate optional range of ηcan’t be determined. It is difficult to select a reasonable ηto perfectly cover the effect of uncertainty and disturbance. If ηis too small, the control system lacks robustness. If ηis too large, the effect of uncertainty and disturbance will be excessively compensated so that active joints torque is very large.

In conclusion, the TSMC has two disadvantages: (A)Eliminating chattering with continuous switching to the sliding mode manifold will deprave the robustness of control system. (B) As the robust parameter for TSMC, ηis difficult to be determined with unknown uncertainty and disturbance. Unreasonable ηmay take away control stability and robustness, or excessively compensates the effect of uncertainty and disturbance. Therefore, we need to propose a more effective underactuated control method for the space manipulator with free-swinging joint failure.

3.2.2. Invariance of controlled variables converging to the desired states

We give Theorem II to discuss the stability of the second convergence stage.

Theorem. When the nominal inertia matrix ^Mis full rank,the convergence of controlled variables along the sliding mode manifold is invariant to the effect of model uncertainty and torque disturbance.

Proof. Expressing the dynamic coupling containing uncertainty and disturbance as

where E∈Ris an identity matrix. As can be seen from Eq. (53), the convergence of controlled variables to desired states is invariant to model uncertainty and torque disturbance. Therefore, if controlled variables have arrived at the sliding mode manifold, they must converge to desired states.

The TSMC the space manipulator with free-swinging joint failure can be robust to model uncertainty and torque disturbance, but its robustness and stability entirely depend on parameter η.coupling to calculate active joints torque.It belongs to an indirect adaptive fuzzy control method which doesn’t directly modify parameters of TSMC. It has three design steps:

Step 1. Fuzzification of crisp inputs s，˙s, and output d.

Step 2. Establishing fuzzy rules and selecting reasonable fuzzy inference, we can infer fuzzy output from fuzzy inputs.

Step 3. Defuzzification of fuzzy output. And adaptively adjusting control parameters according to the compensation effect.

4. Adaptive fuzzy terminal sliding mode controller

In fact, two disadvantages of the TSMC both due to the robustness excessively relies on the selection of η, and ηsat（s）always passively covers the effect of uncertainty and disturbance. If we can estimate the effect of model uncertainty and torque disturbance according to specific controlled states, it can be actively compensated,and the decisive effect of ηselection on control robustness and stability will be obviously weakened.

In this section,we integrate adaptive fuzzy controllerinto the TSMC. Adaptive fuzzy controller utilizes heuristic human knowledge to estimate the real effect of unknown model uncertainty and torque disturbance according to specific behavior of controlled variables, and directly compensate them into active joints torque calculation.To acquire more accurate estimation result,fuzzy control parameters need to be adaptively adjusted according to the practical compensation effect. Fuzzy controller doesn’t require the specific model of system or disturbance, so it serves as an effective control scheme for unknown uncertainty and disturbance for the space manipulator with free-swinging joint.

4.1. Adaptive fuzzy control law

According to stability analysis on the TSMC, model uncertainty and torque disturbance only act on the first convergence stage. Mathematically, the effect of uncertainty and disturbance brings about the deviation position and speed of controlled variables from the sliding mode manifold. Therefore,we can fuzzily infer the total disturbance daccording to current s and ˙s. Then, dis directly substituted into dynamic

4.1.1. Fuzzification of inputs and output

The crisp inputs and output need to be fuzzified into fuzzy words according to their domains. To accord with symmetry of input/output domain, the fuzzy word set usually contains odd number of elements.In this paper,we fuzzify input/output as follow

The input fuzzy sets of S， ˙Sare A and B, and the output fuzzy set of dis C. Then, we allocate membership function for every fuzzy word and ambiguity of the data. It illustrates the fulfilment degree of a crisp value to certain fuzzy word.There are two typical kinds of membership function, namely,the singleton membership function and the nonsingleton membership function. Singleton membership function only maps a crisp input into singleton fuzzy word. It assigns membership value μ（S） of as follow

where S∈A. However, the singleton membership function will bring about discontinuous estimation result. The nonsingleton membership function assigns μ（S）=1 when Sstrictly equals to S, and μ（S） decreases as Smoves away from S. It doesn’t change control continuity. We introduce Gaussian membership functions for elements in fuzzy set.For input S, its Gaussian membership function is

where l denotes the lth fuzzy rule.j represents jth element in fuzzy input set of S.k represents jth element in fuzzy input set of ˙S. h represents hth element in fuzzy output set. ‘‘If” is the precondition, and ‘‘Then” is the conclusion. Traversing all possible fuzzy input value, we can obtain rule base R: ^A×^b →^C containing 7×7=49 fuzzy rules. For example, ^Sis PB and ^˙Sis PB illustrates the effect of uncertainty and disturbance is very large to lead controlled variables to keep away from the sliding mode manifold.Thus,the fuzzy rule should be

We can obtain fuzzy output according to membership function value in Eq. (64).

Table 1 Fuzzy rule base between ^Si，^˙Si and ^di.

4.1.3. Adaptive defuzzification of fuzzy output

The fuzzy output needs to be defuzzified as the crisp output.Defuzzification method matching with Mamdani inference mechanism is the Gravity method. It has high accuracy.

To acquire more accurate estimation result closing to the real effect of model uncertainty and torque disturbance, we update Δwith rate

The AFTSMC structure is shown in Fig. 5.

4.2. Analysis on stability and robustness of the AFTSMC

Fig. 5 AFTSMC scheme.

5. Simulations

In this section, the space manipulator with free-swinging joint failure executes some typical on-orbit tasks based on the TSMC and the AFTMSC, respectively. Then, the advancement of the AFTMSC is verified by comparing task execution effects.

Simulation experiments are carried out surrounding SSRMS type7-DOF space manipulator in Fig. 6. Its kinematic and dynamic parameters are in Tables 2 and 3.

5.1. Task execution simulation on the TSMC

We direct the space manipulator with free-swinging joint failure to execute passive joints regulation task, and a combination task of limiting base attitude disturbance when regulating passive joints based on the TSMC.

5.1.1. Passive joints regulation

Fig. 6 SSRMS type 7-DOF space manipulator.

Table 2 Kinematic parameters of SSRMS type 7-DOF space manipulator.

Table 3 Dynamics parameters of the 7-DOF space manipulator.

Fig. 7 Passive joints angle and sliding mode value with η1 =η2 =1.5 in TSMC.

Utilizing Point-to-Point control mode.To avoid singularity of the TSMC, we set P=P=3 q=q=5 α=α=0.1,k=k=0.1 and η=η=1.5 to guarantee strong robustness to above model uncertainty and torque disturbance. Furthermore, we introduce the saturation function in Eq. (28) to eliminate chattering, and set b=b=0.03. Passive joints angle and sliding mode value are shown in Fig. 7.

Fig.7(b)shows the steady states errors of sliding mode values obviously varying with sinusoidal model uncertainty and torque disturbance, so the elimination of chattering truly impairs the robustness. But because ηis very large to absolutely satisfy Eq. (46), it can guarantee passive joints to precisely converge to desired angles, and the controller is strongly robust to uncertainty and disturbance. Active joints torque is in Fig. 8.

Fig. 8 Active joints torque with η1 =η2 =1.5 in TSMC.

Fig.8.shows the excessive compensation is caused by large η,so the active joint torque peak reaches up to-3671.77 N·m,which will be overloaded for many types of space manipulator

5.1.2. Passive joint regulation with base attitude zerodisturbance

The passive joint is required to continuously track desired displacement, velocity and acceleration. Passive joint angle and sliding mode value are in Fig. 9. Active joints torque and base attitude disturbance are in Fig. 10.

θin Fig.9(a)represents the desired trajectory of the passive joint. The passive joint arrives at desired angle and base attitude disturbance is very small,the manipulator finishes this combined task placidly. But owing to η=1 , excessive compensation also exists. Joints torque peak is 29.52 N·m.

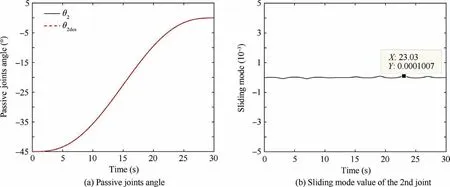
Fig. 9 Passive joints angle and sliding mode value with η1 =η2 =1.0 in TSMC.

Fig. 10 Active joints torque and base attitude disturbance with η1 =η2 =1.0 in TSMC.

The space manipulator with free-swinging joint failure can finish typical space tasks based on the TSMC. Especially, we demonstrate the excessive compensation on model uncertainty and torque disturbance with large η(Fig. 8), and the steady state error caused by robustness degradation because of chattering elimination with continuous switching to the sliding mode manifold(Fig. 7(b)and Fig. 9(b)).

Fig.11 Passive joints angle and sliding mode value with η1 =η2 =0.1 in TSMC.

Fig. 12 Passive joints motion and active joints torque with η1 =η2 =0.1 in AFTSMC.

5.2. Task execution simulation on the AFTSMC

The space manipulator executes same tasks as the TSMC based on the AFTSMC.

5.2.1. Passive joints regulation

Fig. 13 Passive joints motion and active joints torque with η1 =η2 =0.3 in AFTSMC.

Aiming at the same passive joints regulation task in Section 5.1.1,we carry out contrast simulation experiments based on the AFTSMC.To prove the fact that the AFTSMC can be more reliably robust to unknown model uncertainty and torque disturbance than the TSMC, we only decrease η，ηto 0.1 but don’t change other parameters.Under the same uncertainty and disturbance, passive joints angle and sliding mode value are in Fig. 11.

Fig. 14 Passive joints angle and sliding mode value with η1 =η2 =0.05 in AFTSMC.

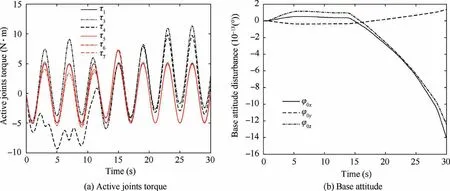
Fig. 15 Active joints torque and base attitude disturbance with η1 =η2 =0.05 in AFTSMC.

Passive joints angle can’t converge to desired value, and sliding mode values can’t converge to zero, which illustrates that ηis too small to cover the effect of uncertainty and disturbance, and the TSMC has lost stability and robustness for.

Passive joints accurately converge to desired angles with η=η=0.1, and the steady state errors in the vicinity of the sliding mode manifold are close to those in Fig. 7(b).Meanwhile, active joints torque peak drops to-1325.19 N·m, which decreases 63.19% compared with active joints torque peak based on the TSMC. Therefore, the adaptive fuzzy controller succeeds in accurately estimating the effect of model uncertainty and torque disturbance at every control cycle, and the controller acquires strong robustness with smaller η.

Although smaller ηcan make passive joints converge with smaller active joints torque, the steady state error in the vicinity of the sliding mode manifold is obvious. Furthermore, small ηcorresponds to slow dynamic response,and fuzzy control overshoot is obvious. It means that we shouldn’t blindly decrease ηonly for acquiring smaller joint torque. For the same passive joints regulation task, if setting η=η=0.3 but maintaining other parameters, passive joints angle, sliding mode values and active joints torque are in Fig. 13.

Passive joints also converge accurately, and active joints torque peak is -1879.21 N·m, still decreasing 48.82% compared with torque peak based on the TSMC. More importantly, steady state errors in Fig. 13(b) fall further than those in Fig.12(b),and the control overshoot is effectively inhibited.Therefore, sacrificing partial optimization effect of active joints torque, the task execution reliability can be observably improved based on the AFTSMC.

5.2.2. Passive joint regulation with base attitude zerodisturbance

The space manipulator finishes the task placidly. The steady state error of sliding mode value almost disappears,and active joints peak drops to 11.34 N·m, decreasing 61.59% compared with torque peak based on the TSMC.

From simulation results,the AFTSMC accurately estimates and actively compensates the real effect of unknown model uncertainty and torque disturbance. Therefore, the selection difficulty of η is avoided,and the control system still possesses strong robustness. Furthermore, because the estimation is coincide with the real effect at every control cycle, the manipulator can execute task with smaller active joints torque. The AFTSMC is very appropriate to underactuated control of space manipulator with free-swinging joint failure with the effect of unknown model uncertainty and torque disturbance.

6. Conclusions

In this paper, we design the AFTSMC to control the freefloating space manipulator with free-swinging joint failure to execute on-orbit tasks under unknown model uncertainty and torque disturbance.We derived the mapping relationships between active joints acceleration/torque and passive joints,free-floating base, EEF accelerations, which make up the dynamic coupling inside the manipulator system. Then, the TSMC which is robust to model uncertainty and torque disturbance is designed, but it has two drawbacks: (A) Control robustness depraves in the vicinity of the sliding mode manifold with eliminating chattering. (B) Under the action of unknown model uncertainty and torque disturbance, the robust control parameter is difficult to be determined. To improve the conventional TSMC, we introduce the adaptive fuzzy controller to estimate the real effect of unknown model uncertainty and torque disturbance, and actively compensate it into joints torque calculation.In this way,selection difficulty of the robust parameter is avoided,and the control robustness is guaranteed.The tasks execution effects based on the TSMC and the AFTSMC are compared, and we point out the AFTSMC is effective for the undeactuated control of the space manipulator with free-swinging joint failure under the action of unknown model uncertainty and torque disturbance. The main contributions in this paper including:

(1) We provide an effective control method for the freefloating space manipulator with free-swinging joint failure, which belongs to a new underactuated multibody system containing hybrid-order nonholonomic constraints for the first time.

(2) The decisive effect of control parameter on robustness of sliding mode control is impaired and the control robustness gets guaranteed by actively compensating model uncertainty and torque disturbance with the AFTSMC.

(3) With accurate estimation of model uncertainty and torque disturbance, active joints can compensate uncertainty and disturbance with the smaller torque.

(4) In future research, we will we will introduce joint/link flexibility to study modelling and control method for the space manipulator with free-swinging joint failure,and pay more attention to the optimal control theory with the help of‘‘passive redundancy”when active joints are more than DOFs of controlled units.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This study was co-supported by the Fundamental Research Funds for the Central Universities of China (No. 2019PTB-012) and the National Natural Science Foundation of China(No. 51975059).

Appendix

Kinematic and dynamic modelling of the space manipulator with free-swinging joint failure

A.1. Derivation of the Jacobian matrix