Effects of wing flexibility on aerodynamic performance of an aircraft model

Qinfeng GUO, Xi HE, Zhuo WANG, Jinjun WANG

Key Laboratory of Fluid Mechanics, Ministry of Education, Beihang University, Beijing 100083, China

KEYWORDS Aerodynamic forces;Flexible wings;Flow field;Fluid structure interaction;Wing tunnel tests

Abstract The low-speed wind tunnel experiment is carried out on a simplified aircraft model to explore the influence of wing flexibility on the aircraft aerodynamic performance.The investigation involves the measurements of force,membrane deformation and velocity field at Reynolds number of 5.4×104–1.1×105. In the lift curves, two peaks are observed. The first peak, corresponding to the stall, is sensitive to the wing flexibility much more than the second peak, which nearly keeps constant.For the optimal case,in comparison with the rigid wing model,the delayed stall of nearly 5° is achieved, and the relative lift increment is about 90%. It is revealed that the lift enhanced region corresponds to the larger deformation and stronger vibration, which leads to stronger flow mixing near the flexible wing surface. Thereby, the leading-edge separation is suppressed, and the aerodynamic performance is improved significantly. Furthermore, the effects of sweep angle and Reynolds number on the aerodynamic characteristics of flexible wing are also presented.

1. Introduction

In the field of aircraft design, better aerodynamic characteristics are the relentless pursuit of designers. Traditionally, the flaps are always used to change the camber and the area of wing to provide additional lift at low speed, and the ailerons provide the moments through the asymmetric torsion of wing.In recent years, morphing, which refers to the vehicles’ ability to achieve seamless outer shape change, has attracted more and more attention.Although from the aerodynamic perspective,the advantages of morphing wing have long been recognized, the designing complexity, as well as a series of technical challenges, limits its practical application.

The membrane flexible wing, as one of the passive morphing wings, is a capable technology to maintain the optimal aerodynamic characteristics over a broad range of flight conditions.The origination of membrane flexible wings goes back to the beginning of human flight, the Wright Brothers’ flyer.They used the compliant membrane as lifting surfaces and controlled the roll through wing wrapping. In the following decades,because of the revolution in both commercial and military aviation,the original membrane was replaced by the stiffer structures, such as rigid wings and metal control surfaces.Till more recently, with the prosperity of Micro Air Vehicles(MAVs) and Unmanned Aerial Vehicles (UAVs), the membrane flexible wings showed the substantial potential application again in aircraft design.

For the MAVs and UAVs,most of the early works concentrated on the manufacture of flexible wing, and some of them have achieved successful flights.They combined the rubber membrane with the carbon fiber skeleton to create the aircraft with a flying wing. It was shown that the flexible wing could deform and vibrate to optimize its aerodynamic characteristics to meet different mission requirements.

To further investigate the mechanism of flexible wing,Song et al.proposed a bioinspired compliant membrane wing and conducted the study of flexible membrane airfoil. The aerodynamic differences between rigid and flexible wings were compared. Later, Hu et al.focused on the membrane wings with free trailing edge and found that trailing-edge deflection resulted in a reduction of the effective angles of attack. This reduction delayed airfoil stall at high angles of attack. At this stage, the computational simulations were also conducted based on the two-dimensional assumption. Gordnierand Tiomkin et al.calculated the mean deformation and the unsteady response of membrane airfoil, and found that the membrane oscillations positively contributed to the airfoil aerodynamic characteristics.

Gordnier et al.investigated the lift enhancement over flexible nonslender delta wing. Various experimental methods were used to analyze the characteristics of three-dimensional flexible wing as well as the rigid wing.The results showed self-excited antisymmetric vibrations of the nonslender delta wing promoted reattachment of the shear layer,which resulted in the lift enhancement. Moreover, the stall characteristics were discussed in the works of Liuand Wang et al.The surface oil flow visualization demonstrated that the stall of flexible delta wing was accompanied by the helical flow structure,while the vortex bursting appeared for the rigid wing.

For the aerodynamic performance of the three-dimensional membrane wing,Be´guin et al.carried out a series of studies on a semi-span model with the sweep angle changed morphing wing. It was shown that, after varying the dynamic pressure and the pre-stress,the camber and thickness of the wing could be influenced to some extent. Meanwhile, the variation of the wing planform effectively altered the lift and drag characteristics.In such a way,the relatively high lift to drag ratio could be maintained in a broad range of flight conditions.Based on the improvement of the baseline model, the pre-stress was modified by moving the trailing edge spar. It was obtained that small pre-stress could lead to a larger efficiency at low freestream dynamic pressure and vice versa.

In this paper, a simplified aircraft model is designed with the sweep angle changed membrane wing. The influence of sweep angle, Reynolds number, and membrane flexibility on the aircraft aerodynamic characteristics is investigated. The angle of attack α is from 0° to 60°. In order to further reveal the mechanism behind the enhancement of the flexible wing aerodynamic performance, the velocity field for both rigid and flexible wings, as well as the membrane deformation, is measured at the sweep angle Λ=15°.

2. Experimental setup

The experiments were conducted in the open circulation lowspeed wind tunnel D1 at Beihang University.This wind tunnel has a 1.45 m long oval test section with 1.02 m×0.76 m inlet and 1.07 m×0.82 m outlet. The axis of the test section is 1.45 m high away from the ground.The maximum free stream velocity is 50 m/s,which is driven by the stepless direct current motor. The experimental free stream velocity is fixed at 20–40 m/s.

2.1. Model design

Fig. 1 Sketch of experimental model.

The sweep angle is changeable for the simplified aircraft models with both flexible and rigid wings. The designed fuselage has a total length of 219.3 mm, and a diameter of 40 mm.The axial section of nose is elliptical, and the leading edge of wing root is 101.3 mm away from the nose. Fig. 1(a) is the schematic sketch of the model, showing that the leading-edge sweep angle of the wing Λ is 15°.The inner part of leading edge is straight,and the outer side adopts an elliptical transition.As shown in Fig.1(b),the flexible wing consists of a rigid leading edge and an extendable trailing edge, over which the flexible membrane is spanned. The rigid leading edge is hinged to the fuselage and controlled by two YINYAN ES08MA II Metal Analog Servos. The thickness of leading edge is 3 mm,and the Λ is adjusted between 15° and 30° with an interval of 5°. Similarly, the diameter of trailing edge is also 3 mm. The length of wing root cis 39.5 mm, and the corresponding span L with Λ is shown in Table 1. As shown in Fig. 1(c),the membrane is attached to the rigid leading edge plainly when Λ is 15°. At the trailing edge, the membrane is wrapped around it, but not attached to ensure the membrane deforms smoothly. The fuselage and rigid leading edge are both made of aluminum (LY12CZ). Two different membrane materials are used in the experiments, which are Polyethylene (PE) with a thickness t=0.01 mm and Acrylonitrile Butadiene Styrene(ABS) with a thickness t=0.04 mm, and Young’s modulus is 173.56 MPa and 656.32 MPa, respectively. In the previous works, different dimensionless parameters were proposed to indicate the relative flexibility.In Table 2, the aeroelastic parameter Π=(Et/qc), where q is the free stream dynamic pressure, is shown.The membrane of t=0.01 mm is relatively more flexible, and the one of t=0.04 mm is less flexible. The flat plat rigid wing, which is made of aluminum (LY12CZ) with a thickness of 3.0 mm,has the same planform configuration with the flexible wing.FW1, FW2 and RW are used to mark the less flexible wing,the more flexible one and rigid wing, respectively.

2.2. Force measurement

For force measurement, the model was supported by a sixcomponent strain balance. As shown in Fig. 2, the balance was installed at the tail of the model and disposed inside with a taper fit. The force results were obtained by averaging 2000 sampling points within 20 s. The angle of attack α was controlled by a mechanism varying from 0° to 60° with an accuracy of 0.05°. The maximum blockage ratio was 2.2%obtained at α=60°, which is less than the critical value 5%.Therefore, the blockage correction is neglected. The interval of α was 1° for small value and 2°for high one. The Reynolds number based on the length of wing root was Re=5.4×10–10.8×10. As measured by repeated experiments, the uncertainty was less than 3%.

2.3. Particle image velocimetry

To reveal the mechanism behind the improvement of the flexible wing aerodynamic performance, the velocity field of bothrigid and flexible wings with Λ=15°was measured by Particle Image Velocimetry(PIV).The MicroPIV system was adopted,which employed a Charge Coupled Device (CCD) camera, a Nd:YAG double-pulsed laser as a light source, and Ethylene glycol droplets as tracer particles. The laser power was 500 mJ, and the wavelength was 532 nm. The resolution of the CCD camera was 2456×2058 pixels to capture the field of view of about 100 mm×80 mm resulting in the magnification of 0.04 mm/pixel. The time interval between two straddle frames was 20 μs, and the sampling frequency was 4 Hz. 5000 instantaneous velocity fields were obtained in a single experiment. The tracer particles with a mean diameter of 1 μm were spread in the wind tunnel expansion section. To obtain the velocity fields, the multiple iterative Lucas-Kanade algorithm was used to process the raw practical images with 75%overlap and final interrogation areas of 32×32 pixels.The laser sheet and CCD for PIV measurement are shown in Fig. 2.The measured section was the wing mid-span location, which was 57.4 mm away from the wing root, and the experimental Re was fixed at 5.4×10.

Table 1 Span of model with different sweep angles.

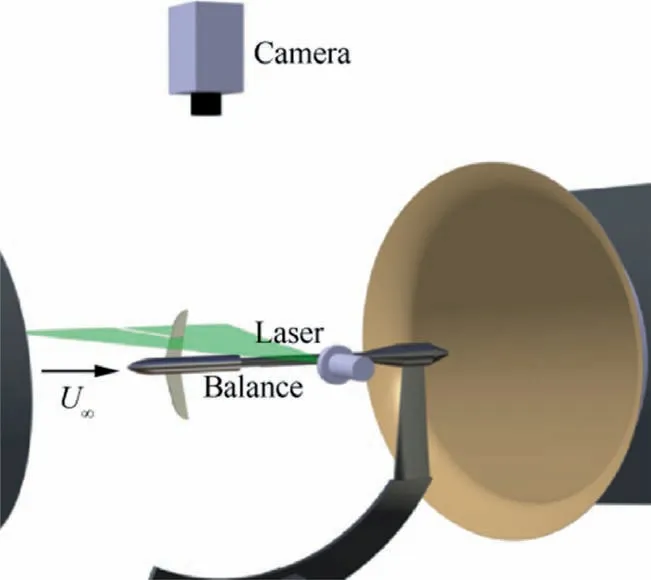
Fig. 2 Schematic sketch of PIV experiment and deformation measurement.

2.4. Deformation

Membrane deformation was measured with a Fastcam Photron SA2 CMOS camera and a continuous laser source. The arrangement of camera and laser was the same as in the PIV measurement, as shown in Fig. 2. The resolution of camera was 2048×2048 pixels with the 90 mm×90 mm field of view,which resulted in the 0.04 mm/pixel magnification. The power of laser was 8 W, and the wavelength was 532 nm. The deformed configuration was recognized using the boundary recognition algorithm,and the pixel coordinate was converted to physical coordinates by the calibration.The upper surface deformation of the flexible wing was captured, where the measured section and experimental Re kept the same as in the velocity measurement, i.e. Re=5.4×10.

3. Results

Table 2 Aeroelastic parameter of flexible wing.

In this investigation, the effects of wing sweep angle Λ, Reynolds number Re and membrane flexibility on aerodynamic characteristics of the flexible wing are considered. Since the model is symmetric,the longitudinal aerodynamic characteristics,especially the lift and drag,are primarily focused.Furthermore,the mechanism behind the flexible wing lift-enhancement is investigated based on the membrane deformation and flow structure at Λ=15° and Re=5.4×10.

3.1. Aerodynamic characteristics of flexible wing

3.1.1. Effects of sweep angle

Fig. 3 shows the lift curves with Λ=15°-30° at Re=10.8×10, and two peaks are observed. The first one is occurred at α=10°-20°, and the second peak at α=40°-44°. The first peak is caused by stall, accompanied with the separated flow and suddenly decreased lift, which is widely identified.For the second one, although similar phenomenon has shown in many works about the airfoil aerodynamic characteristics,its causes were less investigated.Michos et al.worked on the pressure distribution of NACA0012 airfoil at high angle of attack, and they observed that the suction on the upper surface increased with the development of α beyond the stall.Zhou et al.predicated the second peak using the product of the midpoint pressure and the wing area projected on the freestream direction.They assumed that the pressure is increased as α increases after the stall,while the area is monotonically decreased.As a result,the maximum value around α=45° was produced by the coupling influence of two factors. Two lift peaks were also observed in the aerodynamic performance of the swift’s wing model, which indicated that this characteristic also existed in the whole aircraft model at moderate Reynolds numbers.For the aircraft model with membrane flexible wing, this phenomenon is also observed.

The expressions of the two lift peaks are slightly different without the explicit segmentation in most articles.In the works of Rainbird et al.,the lift was divided based on the angle of attack.The lift at α=10°-20°was called the immediate vicinity of stall,and the part of α>20°was called the deep stall.In this classification, the same criteria for all experimental cases could not reflect the mechanism precisely. This paper divides Cinto four regimes. Before the first peak of C, the lift is called the pre-stall regime.In this part,the wing has not stalled and the flow has not completely separated. It should be noted although the Cis non-linear due to the effects of separation and other factors,the overall relationship is still approximately linear. When the α exceeds the first peak, it is called the poststall regime.Specifically,the lift between the first peak and the recovery point is called the immediate vicinity of stall. Then,the Cbefore the second peak is called the increase regime of deep stall.In the increase regime of deep stall,the increased Cis dominated by the increased suction and accompanied by the significant nonlinear characteristic.The rest of Cis called the decrease regime of deep stall.Compared with the previous one, the monotonically drop of Cis dominated by the decreased projected area. In Figs. 3–8, four parts are marked respectively in black, red, blue and magenta points. As for the two lift peaks, the first one is occurred at stall angle α,and the corresponding lift is called C. The second peak is called post stall peak, and the corresponding lift is called the maximum lift coefficient Cat angle of attack of α. It should be noticed the nomination of Cis only valid in this paper.The maximum lift coefficient may occur at the first peak when the circumstance is changed.

Fig. 3 Effects of Λ on CL of FW1 at Re=10.8×104.

Fig. 4 Effects of Λ on Cm of FW1 at Re=10.8×104.

Fig. 5 Effects of Re on CL of FW1 with Λ=15°.

Fig. 6 Effects of Re on drag polar of FW1 with Λ=15°.

Fig. 7 Effects of membrane flexibility on CL of the wing with Λ=15°.

Table 3 shows the lift coefficient variation with Λ at Re=10.8×10. The first one, the slope of lift curve C,reflects the trend of pre-stall regime, and the other coefficients reflect the characteristics of two lift peaks.Cis obtained with the linear polynomial fitting to the pre-stall regime. It can be seen that Cgradually decreases with the increase of Λ,which is consistent with the conclusion of the conventional rigid wing.For the first peak,the stall angle αand the lift coefficient at stall angle Cincrease with the increase of Λ,and they vary from C=0.704 at α=14°to C=0.775 at α=22°with the increment of Cof nearly 10%. As for the second peak,the αin this paper, is between 40° and 44°. The Crises from 0.945 at Λ=15° to 0.986 at Λ=30°, increasing by 4.3%. Comparing the two peaks, the first peak is more sensitive to the Λ, which indicates the membrane flexibility influence more intensively on the stall.

Fig. 4 shows the variation of nose-up pitching moment Cwith Λ. The Cis measured about the nose of aircraft model.Overall, the aircraft model shows the static stability except from some specific angles around the first peak of lift coefficient.More precisely,Cis not only influenced by C,but also by the sweep angle.For the pre-stall regime,Cis nearly consistent with C, which means the increased Cleads to the increased absolute value of C.Similarly,the immediate vicinity of stall corresponds to a lesser extent decrease of C, even to a small fluctuation. In the following part, the influence of sweep angle appears. The larger the sweep angle, the more backward the resultant force. Furthermore, the decrease of Cafter the second lift peak may relate to the influence of fuselage.

Fig.8 Effects of membrane flexibility on drag coefficient CD and lift to drag ratio K with Λ=15° at Re=5.4×104.

Table 3 Statistical results of lift curves of FW1 at Re=10.8×104.

3.1.2. Effects of Reynolds number

Fig. 5 shows the lift curves at Re=5.4×10, 7.1×10, and 10.8×10with Λ=15°.Different from the conventional rigid wing, aerodynamic characteristics of flexible wing model is much more sensitive to Re. At the pre-stall regime, Cdecreases as Re increases, corresponding to 3.96, 3.04, and 2.89 rad, respectively. This variation is caused by the different membrane deformation, as well as the different camber.Meantime,the first lift peak is also influenced.With the raising of Re, the stall angle αis 9°, 13°, and 14°, and corresponding lift coefficient Cis 0.639, 0.666, and 0.704, respectively. For the second peak, Cincreases from 0.898 to 0.945 with a relative increment of 5.2%, while αhas been maintained between 40° and 44°. In addition, an increase in Re can result in better deep stall characteristics.

Fig.6 is the drag polar at different Re with Λ=15°.It can be seen that the zero-lift drag increases with Re in this investigation, from about 0.110 at Re=5.4×10to 0.176 at Re=10.8×10. Moreover, stall can be clearly observed. In immediate vicinity of stall, the Ccorresponding to the same drag coefficient Cbecomes larger as Re increases, which is closely related to the delay of stall and the improvement of lift coefficient.

3.1.3. Effects of membrane flexibility

Fig. 7 shows the lift characteristics of rigid wing model (RW),as well as flexible wing models (FW1 and FW2) at Λ=15°.Compared with the rigid wing, the flexible wings delay stall,enhance the lift coefficient at the stall angle, and result in a substantial improved lift performance around the first peak.The stall of rigid wing model occurs at about α=5°, while it approaches α=10° for the flexible wing. When Re=5.4×10, αas well as Cof FW2 is higher than that of the other two models.The lift improvement is obvious near α=10°, at which Cincreases from 0.362 to 0.688 with an increment of 90%.At Re=10.8×10,the FW1 shows better lift characteristics because of the higher Cstarting from α=5°. Specifically, Fig. 9 shows the differences of lift coefficient ΔCbetween FW2 and FW1. The part of ΔC>0 reveals the more flexible wing is superior to the other one.As shown in Fig. 9, with the increase of Re, ΔCgradually turns from positive dominant to negative dominant.The more suitable flexible wing is changed from more flexible to less flexible. Therefore, within the experimental conditions, the more flexible the wing, the better the lift characteristics at lower Re, vice versa.

It can be seen from Fig. 8(a) that the increase in the lift of flexible wing is at the expense of drag penalty. The zero-lift drag and the drag due to lift of the flexible wing are both larger than that of the rigid wing,so the maximum lift to drag ratio is not enhanced as much as lift. Under the experimental condition, the maximum lift to drag ratio of FW1 is close to that of the rigid wing, which is 4.25 and 4.26, respectively. Benefiting from the delayed first stall, angle of attack corresponding to the maximum lift to drag ratio is delayed from 4° to 8°.As a result,the flexible wing can provide a more significant lift while still ensuring the relatively high efficiency.Since the FW1 is superior to the FW2 in the maximum lift to drag ratio,accompanied by the approximately similar lift as well as the stall angle,this model will be further analyzed in the following sections to investigate the mechanism behind the improvement of flexible wing aerodynamic characteristics at Re=5.4×10.

Fig.9 Difference in lift coefficient ΔCL between FW2 and FW1.

3.2. Flexible wing deformation

The membrane deformation reflects the effects of the aerodynamic force on the flexible wing, while the deformed wing reacts to the flow field that changes the aerodynamic characteristics. Since the lift is mainly provided by the suction force on the upper side of the flexible wing,the upper surface membrane deformation at the wing mid-span location was measured.The membrane curves are shown together with the flow fields. In Fig. 10, the statistical results of the membrane deformation D/cis presented.The points show the time-averaged deformation of the midpoint along the direction perpendicular to the chord direction, and the bars reflect the vibration amplitude of that point.Although the midpoint deformation cannot fully reflect the deformation of the whole airfoil, the tendency can still be revealed.

In the pre-stall regime, the time-averaged deformation is positively correlated with α. This increase is resulted from the gradually increased suction force on the flexible upper surface. Under the measured condition, the time-averaged deformation reaches the maximum value near α=10°,at which the lift is most obviously enhanced.The bars show that the flexible wing encounters the strong vibration near α=2° and 10°. At α=2°, the leading edge separation still exists because of the blunt leading edge, while the deformation of the flexible wing is small. The large membrane fluctuations at this angle of attack is mainly due to the aerodynamic loading and the bistable nature of flexible membrane.As α increases,this vibration gradually decreases until the near region of the first lift peak. The second peak of vibration amplitude is shown at α=10°, which is around the stall and the lift obviously improved region.It is revealed that the significant lift improvement corresponds to larger deformation and stronger vibration,and this will be further discussed in the following section.

3.3. Velocity field

Fig. 10 Deformation D/croot at the midpoint of flexible wing upper surface.

Fig. 11 Time-averaged streamlines at α=6° and 10°.

Figs. 11 and 12 show the time-averaged streamlines, in which the red lines show the time-averaged deformation of the flexible wing upper side. For the flexible wing in the following figures, the initial flat part of upper surface is caused by the attachment between the rigid leading edge and the flexible membrane.For the rigid wing,it maintains the initial configuration during the whole experiment. The results of the flexible wing are selected for α=6°, 10°, 20°, and 40°, corresponding to the pre-stall regime, the immediate vicinity of stall, the increase regime of deep stall, and the region close to the decrease regime of deep stall,respectively.In order to compare with the flexible wing,the results of the rigid wing at the same α are also presented.

As shown in Fig. 11, the deformation and vibration of the flexible wing upper surface can effectively suppress the flow separation, thereby increasing the Cof flexible wing. In the works of Be´guin et al.,the results of surface flow visualization showed the development of mid-span sectional flowfield was similar to the most parts of flexible wing. For the threedimensional flexible wing, although the illustrated velocity field cannot totally reflect the flow of the entire wing,it can still reflect the variation of the dominant flow structure. For the rigid wing at α=6°, it is near the first stall accompanied by a visible separation bubble in the upper surface. At α=10°,the flow clearly separates at the blunt leading edge for both rigid and flexible wings. However, the separated flow reattaches to the flexible wing surface, dominated by the attached flow.For the rigid one,separated flow will not reattach downstream, and the whole surface is in the recirculation region.The ability of the flexible wing to maintain the separated flow reattached is the main reason for the significant liftenhancement near α=10°.

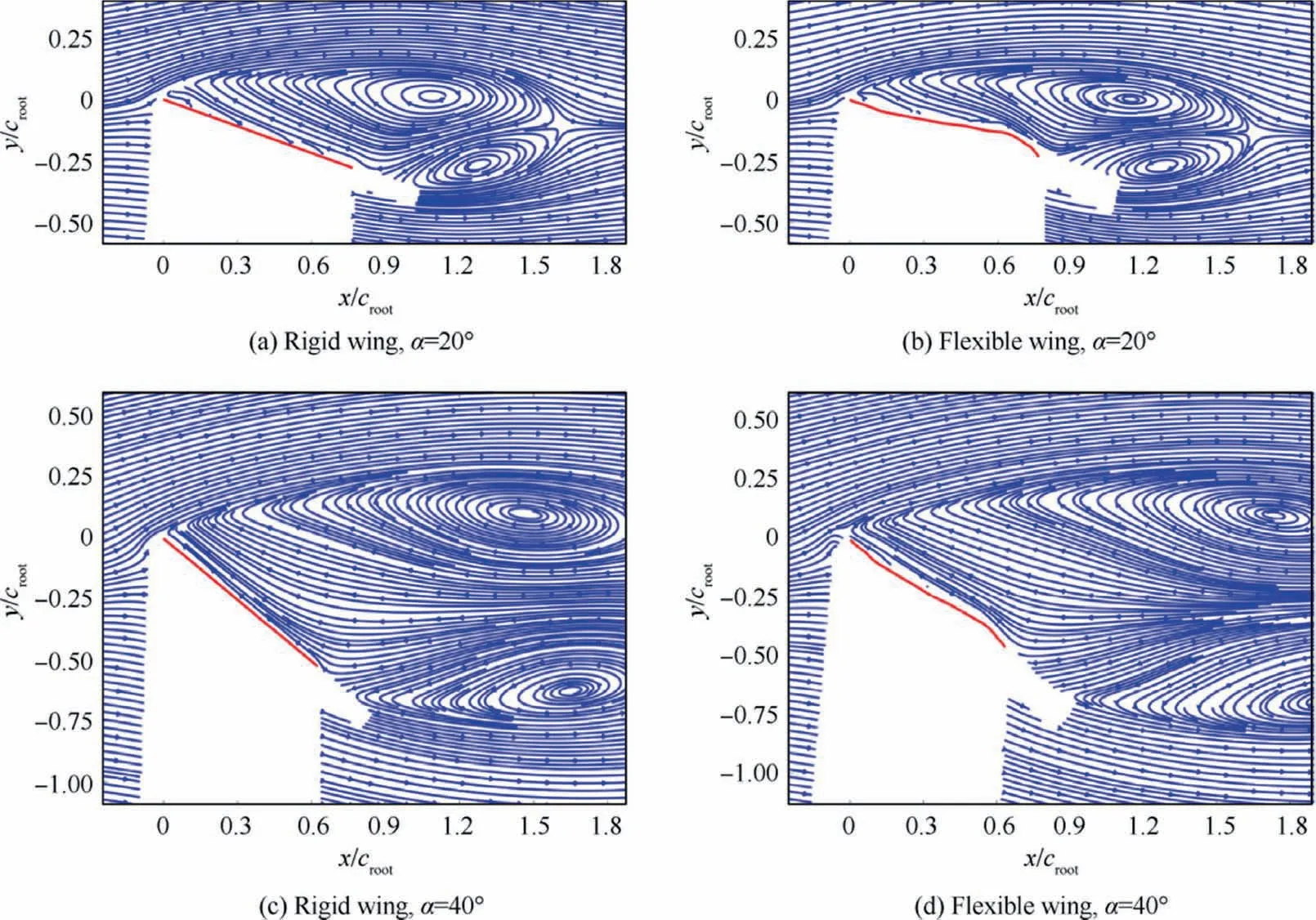
Fig. 12 Time-averaged streamlines at α=20° and 40°.

As shown in Fig.12,the separated flow,as well as the trailing edge vortex, can be observed for both flexible and rigid wings at α=20°. Compared with the rigid wing, the flexible wing still deforms positively, resulting in a positive camber,and has a relatively smaller separation bubble. At α=40°,the deformation of the flexible wing upper surface is significantly reduced, and the Cis close to that of the rigid wing.

Fig. 13 shows the streamwise velocity u/Udistribution near the leading edge at x/c=0.2 and near the wake at x/c=1.5. Since the flexible upper surface is positively deformed in the y direction,the curves of the flexible and rigid wings are not aligned at the lowest point at x/c=0.2. The negative value of streamwise velocity is observed at α=6°for the rigid wing,while it appears at α=10°for the flexible wing.When α=10°, the membrane deformation not only suppresses the leading-edge separation but also increases the streamwise velocity, thereby enhancing the leading-edge suction peak. As α continues to increase, the difference between the flexible and the rigid wings is reduced. At the position of x/c=1.5, the half-width of flexible wing wake is smaller than that of the rigid wing. Especially at α=10°, the halfwidth value is reduced by 15.1%,accompanied by the reduced maximum velocity deficit. The half-width of the near wake region, as shown in Table 4, is determined by the vertical distance between the two points where the mean streamwise velocity falls to half of the maximum deficit.The reduction of the wake deficit is mainly caused by the suppression of the leading-edge separation. At α=20° in Fig. 13(g), the half-width of the flexible wing wake is slightly larger than that of the rigid wing, but becomes obviously wider at α=40°,which indicates the increase of drag.

In summary,the lift-enhancement of flexible wing is caused by the coupling of deformation and flowfield. As shown in Fig.10,the deformation increases positively with the incidenceuntil the first peak of lift coefficient, where the liftenhancement is most obvious.The membrane vibration as well as the deformation reaches the peak value at the angle of attack of 10°. Correspondingly, the turbulent characteristics in Fig. 14 at the same angle of attack indicate there is strong flow mixing near the upper surface of flexible wing.The effects on the time-averaged flowfield are shown in Fig. 11. The separation is obviously suppressed.As a result,the increase of lift coefficient is achieved.

Table 4 Half-width of wing wake at x/croot=1.5.

Fig. 13 Streamwise velocity distribution umean/U∞at different streamwise locations.

Fig. 14 Turbulent characteristics of the flexible and rigid wings at α=10°.

4. Conclusions

To further reveal the influence of flexible wing on the aerodynamic performance of aircraft and the mechanism behind this phenomena, the wind tunnel experiments including the measurements of force,flow field and membrane deformation were conducted on a simplified aircraft model with flexible and rigid wings.The experimental parameters,including the sweep angle,Reynolds number,and membrane flexibility,were investigated at angle of attack of 0°-60°.At the end,the mechanism behind the aerodynamic performance improvement of the flexible wing was explained. The main conclusions are as follows.

(1) Two peaks are observed in lift curves.Based on this phenomenon, the lift curve is divided into four regions,including the pre-stall regime, the immediate vicinity of stall, the increase regime of deep stall, and the decrease regime of deep stall.

(2) The slope of the lift curve decreases with the increase of the sweep angle. At the same time, the stall angle is increased. Different from the rigid wing, the aerodynamic characteristics of flexible wing are clearly influenced by Reynolds number, including the decreased slope of lift curve in the pre-stall regime, the delayed stall angle, and the improved first lift peak. The increased Reynolds number can make the experimental flexible model have better deep stall characteristics.Furthermore,compared with the rigid wing,lift characteristics of the flexible wing are improved with delayed stall and enhanced lift with maximum relative increment of 90%.Under the experimental conditions, the more flexible wing is more suitable at lower Reynolds number,and vice versa.

(3) The improvement of the lift performance of the flexible wing is caused by the interaction of membrane deformation and fluid structure. Firstly, the stall of the model is closely related to the enlargement of the leading-edge separation. Moreover, for the flexible wing, significant lift improvement corresponds to larger deformation and stronger vibration. Due to the membrane deformation, the stronger mixing near the upper wing surface is observed and the flow separation is suppressed. As a result, the lift characteristic is improved.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Nos. 11761131009 and 11721202).