边缘计算系统中资源分配防策略拍卖机制设计 *

池来新,杨旭涛,谢 宁,张学杰

(云南大学信息学院，云南 昆明 650000)

1 引言

1.1 问题的提出

云计算[1]是最近十多年间流行的计算模式，它将大规模的计算资源(CPU、内存、磁盘存储等)集中起来，可以通过通信网络方便地为用户按需提供计算服务。但是，随着物联网技术和移动互联网的发展，人们对于计算任务的需求更加丰富，云中心数据压力不断增大，同时通信网络存在延迟性高的特点，传统的云计算模式已渐渐不能满足现今庞大而多样化的任务需求，而边缘计算[2]的出现则能有效地解决这一问题。

边缘计算是传统云计算的改进计算模式，它在保留云计算中心的计算能力之外又在靠近用户的网络边缘部署一定量的计算资源，通过缩短与用户的物理距离克服了云计算高延迟的问题，同时对于时延要求低的任务仍可以放在云中心执行，数据的分流也有效地缓解了传统云计算中数据中心压力大的问题。边缘计算的资源提供商可以通过虚拟化技术[3]将各种计算资源整合在一起，以虚拟机的形式为用户提供服务，提高用户的体验质量，由于边缘计算资源提供商的资源容量有限，为了能取得最大利益，边缘计算资源提供商需要合理地针对用户所提交的资源需求和报价进行资源分配。

目前主要有2种资源分配方式，一种是传统的分配方式，即由资源提供商设置好虚拟机配置和对应价格供用户进行购买使用；另外一种即基于拍卖的方式，由用户提交资源需求和报价来通过竞争使用资源，资源提供商会根据最大化社会福利(拍卖获胜用户的报价之和)的目标计算出拍卖获胜用户和他们应该支付的价格。基于拍卖的方式使得资源的分配和定价更加灵活，可以充分利用资源提供商的闲置资源，提高了资源提供商的资源利用率和社会福利。但是，这增加了计算模型的复杂性，且难以确定用户的最终支付价格；同时，用户往往会通过诸如虚报资源需求和报价等策略性行为来用更低的价格获取同样多的资源，或以同样的价格获取更多的资源，这损害了资源提供商的利益。所以，如何设计一个防策略拍卖机制也是一个重大挑战。

1.2 相关工作

边缘计算环境下的防策略拍卖机制主要需要解决3个问题，即资源分配算法的设计(拍卖获胜用户的确定方法)、用户支付价格的确定和防策略拍卖机制的实现，下面将在上述3个方面分别阐述相关研究工作。

(1)在资源分配算法方面。文献[4,5]提出了一种在云计算环境下针对虚拟机的组合拍卖机制，给出了资源分配近似算法，但该算法仅能针对资源类型单一的虚拟机进行分配，且算法仅适用于云环境。文献[6]详细介绍了移动边缘计算资源分配中的一些常见策略，主要包括最小化时延、最小化能耗和最大化收益3种类型。文献[7]研究了移动边缘环境下在移动蜂窝网络中的资源分配算法，但算法未能同时考虑云端和边缘端的资源分配。文献[8]提出了云计算环境下的虚拟机分配贪婪算法并给出了算法近似比，该算法运算速度快，且能够满足防策略。文献[9,10]提出了云计算环境下支持多需求的资源分配算法，可同时兼容传统的单一需求情况。文献[4,5,8-10]提出的算法均能满足防策略，可以给边缘计算的防策略机制实现提供参考。文献[11]提出了基于改进粒子群算法的资源分配策略，能够在较短时间内取得较好的实验结果，但该算法具备一定随机性，在拍卖机制中无法保证防策略。

(2)在支付价格计算方面。文献[12,13]将经济学中的VCG(Vickrey-Clarke-Groves)理论用于拍卖机制中的支付价格计算，并给出了大量理论铺垫。文献[14]在网格计算中使用VCG理论进行资源定价，使得资源拍卖机制实现了防策略，但通过VCG理论进行定价是一个NP难问题，计算时间耗费太大，难以用于实际场景中。文献[8]在资源分配算法为满足单调性的贪婪法的前提下，提出了基于临界价格的支付价格算法，该支付算法使得拍卖机制满足了防策略，同时计算速度相比基于VCG理论的支付价格算法要快。文献[9，10]采用二分法计算基于临界价格的支付价格，使得算法性能得到进一步提高。

(3)在防策略拍卖机制设计方面。文献[15]详细介绍了防策略拍卖机制设计的相关原理并对防策略拍卖机制的实现给出了理论推导。文献[8,16]分别提出了在云计算环境下基于单调性和临界价格理论的离线和在线2种情况下的防策略拍卖机制。文献[17,18]提出了云计算环境下资源异构时的防策略拍卖机制，能解决多服务器资源分配的问题。文献[19]提出了在包含多个资源提供商的情况下的双向防策略拍卖机制，在资源提供商合理选择获胜用户的同时用户也需合理地选择资源提供商。文献[20]提出了移动区块链同边缘计算相结合的最优拍卖机制。文献[21]提出了一种基于边缘计算环境的无嫉妒拍卖机制，该机制可以保证资源分配公平，但无法最大化资源提供商的社会福利。

综上所述，在资源分配的防策略拍卖机制的问题上，已有许多积极的研究成果，但当前研究在边缘计算环境下的资源分配求解、支付价格的计算和防策略拍卖机制的实现方面仍存在较大挑战。在资源分配求解方面，边缘计算平台除了保留有云端的资源服务器外还增加了边缘端的资源服务器，不同的用户也会对于资源的部署位置有着不同的要求。因此，资源分配算法还需合理地选择将用户的资源在云端还是边缘端进行分配，这给资源分配算法的设计增加了难度。在支付价格的计算方面，传统基于VCG理论的定价算法计算时间太长，而基于临界价格的定价算法虽能提高计算速度，但在边缘计算环境下用户的支付价格还需考虑用户的资源部署约束，这成为了边缘计算环境下定价算法设计的一大挑战。在防策略拍卖机制设计方面，现有研究中均通过单调性和临界价格理论来保证拍卖机制满足防策略，但这些研究均要求将云资源抽象为资源池(或一台服务器)进行资源分配才能满足单调性，而边缘计算环境下云端和边缘端的服务器具有不同的特性(如时延、传输能耗不同)，无法将两者进行整合，这使得边缘计算环境下拍卖的单调性难以满足，这成为了边缘计算下的防策略拍卖机制设计中的一大挑战。

1.3 本文贡献

本文研究了边缘计算环境下的资源拍卖机制问题，对边缘计算环境下的资源分配问题进行了数学建模，提出了最优拍卖机制和贪婪拍卖机制2种防策略拍卖机制，可以解决边缘计算中的资源分配问题和支付价格确定问题。其中最优拍卖机制能取得资源分配的最优结果，但由于求解最优解需要消耗大量计算时间而导致应用场景受限，所以还需要提出贪婪拍卖机制，能够在较短时间内合理地分配资源，同时使得资源提供商取得较大社会福利和收益。

本文对提出的算法进行了仿真实验分析，实验结果表明本文算法在资源提供商的社会福利、收益、资源利用率和计算时间等多方面取得了不错的效果，验证了本文算法的有效性和可行性。

2 问题描述和相关定义

边缘计算系统中包含云端服务器和边缘服务器，通常需要设置服务器集群来建立资源池，以实现资源的虚拟化，云端服务器集群和边缘服务器集群通过建立资源池可抽象为云端和边缘端的2台资源服务器，为用户提供资源进行计算服务。用户可以向边缘计算资源提供商提交资源需求和报价以申请资源，但因为云端服务器和边缘服务器上的资源有限，无法满足所有用户的资源需求，故而边缘计算资源提供商需要合理选择用户进行资源分配，以使得自己的社会福利(拍卖获胜用户的报价之和)最大化。

云端服务器部署在资源提供商的数据中心，具有较大的资源容量，但由于距离实际用户过远，所以具有较大时延，只能满足时延敏感性低的用户需求。边缘服务器部署在用户所在社区附近的通信基站(网络边缘)，仅为该社区提供计算服务，与用户距离近，故而拥有较小的时延，可以满足时延敏感性高的用户需求，同时也可以为时延敏感性低的用户分配资源。将边缘计算的资源分配问题刻画成数学模型进行描述，需要先对问题中的角色进行相关定义。

根据上述定义，可将边缘计算的资源分配问题定义为如式(1)～式(5)所示的线性整数规划模型：

Maximize:

(1)

Subject to:

(2)

(3)

xi1+xi2≤1,∀i∈U

(4)

xi1,xi2∈{0,1},∀i∈U

(5)

(6)

在上述线性整数规划模型中，式(1)为目标函数，用于最大化资源提供商的社会福利，其中x为决策变量(如式(6)所示)，xij=1代表用户i的资源分配在云端服务器 (j=1) 或边缘服务器 (j=2)上，xij=0则代表用户i的资源在云端服务器 (j=1) 或边缘服务器上 (j=2) 不被分配。式(2)～式(5)为约束条件，其中式(2)保证分配在云端服务器上的任务所占用的资源不超过云端服务器上各类型资源的容量；式(3)保证分配在边缘服务器上的任务所占用的资源不超过边缘服务器上各类型资源的容量，式(4)保证用户的资源需求不可分，即一个用户的资源不能同时部署在云端服务器和边缘服务器上；式(5)限定了决策变量xij仅能取值为1或0，分别代表分配资源和不分配资源。因为资源种类有多种，部署服务器也包括云端服务器和边缘服务器2种，同时带有资源的服务器部署约束，所以该问题本质上是一个带有部署约束的多维多背包问题，是一个NP难问题[22]。

3 防策略拍卖机制设计

3.1 防策略拍卖机制设计理论

一个拍卖机制包含资源分配和定价2个阶段。在资源分配阶段中，所有用户提交其资源需求和报价，用户的报价可以看作是用户对其提交的资源需求的一个估值，拍卖机制根据资源提供商的资源容量、用户的资源需求情况和报价来合理选择拍卖获胜的用户而对其分配资源，目的是最大化资源提供商的社会福利，其中社会福利为获胜用户的报价之和。在定价阶段，拍卖机制需要计算出获胜用户需要最终支付的价格，形成资源提供商的最终利润。

在现实情况中，提交资源需求的用户都具有利己性[12]，希望以更低的价格或者低于用户资源需求估值的价格来获取资源，或者以同样的价格获取更多的资源，这些会使得用户产生策略性行为，提交有利于自己的不真实的资源需求和报价，从而使自己获利，这会影响到资源提供商的社会福利，因而需要设计一个防策略拍卖机制。

定义1(用户效用) 用户效用用u表示，定义如式(7)所示：

∀i:ui=vi-pi

(7)

其中，vi表示用户i对提交的资源需求的真实估值，pi为用户最终需要支付的价格。用户效用可以代表用户对拍卖结果的满意程度，从式(7)可以看出，用户效用越大，代表其最终需支付的价格愈加低于用户对资源需求的真实估值，所以用户希望最大化其用户效用。

定义2(个体理性) 如果在一个拍卖机制中，所有用户的用户效用均大于或等于0，如式(8)所示，那么这个拍卖机制是个体理性的，个体理性说明不会产生负的用户效用，这可以鼓励用户参与拍卖。

∀i:ui=vi-pi≥0

(8)

定义3(防策略) 防策略也可以称之为可信或激励相容，如果一个拍卖机制使得用户提交真实的信息报告产生的用户效用比用户提交虚假的信息报告产生的用户效用更大，如式(9)所示，则这个拍卖机制是防策略的。

(9)

防策略是一个拍卖机制中的良好性质，可以激励用户提交真实的信息报告，从而不影响资源提供商的社会福利。

接下来将定义拍卖机制中资源分配算法的单调性，定义单调性之前首先引入用户信息报告之间的偏序关系，当时，即表明信息报告中的报价不小于的报价，信息报告中的每种资源需求量均不大于所对应类型资源的需求量，同时信息报告中的时延敏感性值不大于中的时延敏感性值，如式(10)所示：

(10)

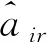
(11)

3.2 最优拍卖机制VMAPEC-OPT

最优拍卖机制VMAPEC-OPT (Virtual Machine Allocation and Pricing for Edge Computing-OPTimal)设计分为最优资源分配算法和最优支付算法2部分。

(12)

(13)

(14)

由文献[12]可知，当一个拍卖机制的资源分配结果是最优解的同时获胜用户的支付价格根据式(12)计算时，则这个拍卖机制是满足防策略的。但是，由于VMAPEC-OPT机制需要求解线性整数规划模型，这会耗费过多计算时间，甚至在用户数量过大的情况下无法计算出结果，使得VMAPEC-OPT机制在实际运用中受限比较大，因而需要设计出计算速度快同时实验效果较好的防策略拍卖机制。

3.3 贪婪拍卖机制VMAPEC-G

3.3.1 VMAPEC-G机制

基于最优拍卖机制VMAPEC-OPT因计算时间过长而难以运用在实际场景中的问题，本文提出了贪婪拍卖机制VMAPEC-G (Virtual Machine Allocation and Pricing for Edge Computing- Greedy)。VMAPEC-G机制同样由分配算法和支付算法2部分组成，首先通过调用资源分配算法VMAPEC-G-A(Virtual Machine Allocation and Pricing for Edge Computing-Greedy-Allocation)计算出社会福利V和资源分配决策变量x，然后对拍卖获胜用户调用临界价格计算算法VMAPEC-G-P(Virtual Machine Allocation and Pricing for Edge Computing-Greedy-Payment)求取用户的支付价格，最后再通过支付价格计算资源提供商的最终收益。

3.3.2 单调资源分配算法

介绍单调资源分配算法时需先引入任务的资源密度，用户的资源密度定义如式(15)所示，代表资源提供商愿意接受用户的程度，用户的资源密度越高时，算法越倾向于给该用户分配资源。

(15)

单调资源分配算法如算法1所示，算法首先需要对所有用户进行用户密度的非升序排序(第3行)，这可以更加充分地利用服务器的资源并实现算法的单调性；然后依次遍历用户并对用户进行资源分配。考虑到时延敏感性高的用户的资源只能分配在边缘服务器，故算法对所有用户优先选择云端服务器进行资源分配(第5行)，这样可以在提高资源利用率的同时提高资源提供商的社会福利；而当用户为高时延敏感性用户时，则会直接选择边缘端服务器进行分配(第6、7行)。分配资源时需要判断服务器上每种类型资源的剩余容量是否能满足用户的需求(第9～15行)，当资源容量均能满足要求时再进行资源分配；同时需要更新对应服务器的剩余资源容量和当前社会福利V以及资源分配决策矩阵x(第16～23行)。为了不对用户重复分配资源，算法需要在第22行跳出第5～25行的for循环。

输出：社会福利V,资源分配决策变量x。

1.V←0;

2.x←0;

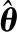
5.forj=1,2do

7. continue;

8.else

9.flag←true;

10.forr=1:Rdo

12.flag←false;

13. break;

14.endif

15.endfor

16.ifflag=truethen

17.forr=1:Rdo

19.endfor

20.V←V+vi;

21.xij← 1;

22.break;

23.endif

24.endif

25.endfor

26.endfor

27.returnV,x.

定理1资源分配算法VMAPEC-G-A满足单调性。

(16)

□

3.3.3 基于临界价格的支付算法

基于临界价格的支付算法如算法2所示，算法需要遍历所有用户，通过决策变量x判断该用户是否拍卖获胜(第2行)，仅当拍卖获胜时才通过二分法进行支付价格的计算(第7～15行)，否则支付价格被设为0(第18行)。二分法由于要不断修改用户的报价，故需先将用户的信息报告暂存起来(第3行)，然后将当前报价上界和下界之和的一半作为新的报价(第6行)，并测试用户是否还能拍卖获胜。当拍卖仍然获胜时，就将当前报价作为新的上界，否则将其作为新的下界，当上下界的差小于一个给定的足够小的ε时，就将支付价格设为当前修改后的报价，其中ε需要小于支付价格的最小单位。

输出:支付价格向量P=[p1,p2,…,pN]。

2.ifxi1=1 orxi2=1

5.lower← 0;

7.whileupper-lower>εdo

9.ifxi1=1 orxi2=1then

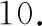
11.else

13.endif

15.endwhile

17.else

18.pi← 0;

19.endif

20.endfor

21.ReturnP.

定理2支付算法VMAPEC-G-P是基于临界价格进行设计的。

证明在支付算法中，当用户i为拍卖获胜用户时，通过取支付价格的上界和下界之和的一半作为当前支付价格，将此支付价格作为用户i的报价再重新判断用户i是否能拍卖获胜，当获胜时以当前支付价格作为上界，否则以当前支付价格作为下界。显然，只要支付价格上界和下界的差控制在预设的数值ε(ε小于实际交易的最小计价单位)之内，即可保证当用户i的报价大于此价格时就会拍卖获胜，小于此价格时就会拍卖失败，根据定义5，此时的支付价格即为临界价格。

□

定理3VMAPEC-G机制是防策略的。

证明根据文献[12]，只要拍卖机制的分配算法满足单调性，并且拍卖获胜用户的支付价格为临界价格，则该拍卖机制是防策略的，由定理1和定理2可证明VMAPEC-G机制是防策略的。

□

定理4VMAPEC-G机制满足个体理性。

证明对于任意的用户i，若用户i拍卖失败，根据支付价格计算算法VMAPEC-G-P可知用户i的支付价格为0，所以用户i的用户效用满足式(17)：

(17)

(18)

综上，根据定义2，拍卖机制满足个体理性。

□

定理5VMAPEC-G机制满足多项式时间复杂度。

□

4 实验

4.1 实验设置

对于虚拟机配置，本文使用了Microsoft Azure[24]的实际虚拟机配置数据，每种虚拟机包含3种计算资源(CPU核心、内存、磁盘)。用户对于虚拟机数量的需求在[1,10]，用户的报价由式(19)进行计算:

(19)

对于资源提供商，本文设置它的云端服务器的CPU、内存和磁盘容量分别为2 000核心，10 000 GB和200 000 GB，边缘服务器的CPU、内存和磁盘容量分别为1 000核心，5 000 GB和100 000 GB。本文按照用户规模从小到大分别针对200,500,1 000,5 000,10 000个用户需求进行测试。

为了体现用户需求的客观性，本文在上述实验配置的基础上模拟了100组用户需求，取其实验结果的平均值作为最终的实验结果。实验还与文献[8]提出的G-VMPAC-II(Greedy-Virtual Machines Provisioning and Allocation in Clouds-II)机制进行了对比。该机制是经典的资源分配拍卖机制，能在较短时间内得出不错的实验结果，但该机制没有考虑边缘计算环境下的资源异构情况，同时还无法在边缘计算环境下满足防策略。实验平台软硬件配置为Windows10操作系统，Intel i7-8550U CPU, 16 GB内存,512 GB固态硬盘存储，编程语言为Java。

4.2 实验结果及分析

4.2.1 社会福利及资源分配时间

社会福利是拍卖机制中获胜用户的报价总和，社会福利最大化是资源分配的目标，同时资源算法需要合理地将计算时间控制在较小范围内，以使算法具备良好的可行性，因此社会福利的结果与资源分配的时间可以直接体现出算法的效果。

图1显示了本文提出的最优拍卖机制VMAPEC-OPT、贪婪拍卖机制VMAPEC-G和文献[9]中G-VMPAC-II机制的社会福利对比结果。由图1可以看出，VMAPEC-OPT机制总能得到最高的社会福利，因为VMAPEC-OPT机制直接对资源分配的线性整数规划模型进行求解，它求出的资源分配结果是最优解；VMAPEC-G机制的社会福利结果介于其它2种机制之间，大约能达到VMAPEC-OPT机制的90%以上；而G-VMPAC-II机制由于未能考虑边缘计算环境下的资源异构和部署约束情况，导致结果比本文提出的2种机制的结果差。同时还可以看出，在用户数目为200的时候，3种机制的社会福利较为接近，因为当用户数目过少时，边缘计算系统的计算资源较为充沛，用户的资源竞争过小，3种机制的差距难以凸显。

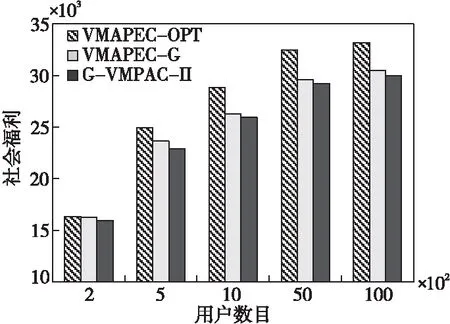
Figure 1 Comparison results of social welfare图1 社会福利对比结果

图2显示了3种机制的资源分配时间对比结果，资源分配时间即社会福利的计算时间。由图2可知，VMAPEC-G和G-VMPAC-II机制的资源分配时间相近且均为较低值，而VMAPEC-OPT的资源分配时间却远高于其它2种机制，甚至在用户数量较少的情况下(200个用户)仍需花费大量的计算时间，这与第3节的分析一致。资源分配最优解的求解为NP难问题，无法在多项式时间内执行，这使得VMAPEC-OPT机制在可行性方面存在较大限制。定理5表明，VMAPEC-G机制中的资源分配满足多项式时间，故而能在较短时间内执行，同时由图1可知VMAPEC-G能取得不错的社会福利结果，故而VMAPEC-G具有极强的可行性。

Figure 2 Comparison results of resource allocation time图2 资源分配时间对比结果

4.2.2 收益及收益计算时间

收益是拍卖机制中获胜用户的支付价格的总和，它能代表资源提供商最终的利润，而支付价格需要在完成资源分配的前提下再由支付算法计算得出，因此，收益计算时间会大于资源分配时间。同时G-VMPAC-II由于在边缘计算环境下无法满足防策略，故其计算支付价格没有意义。

图3显示了VMAPEC-OPT和VMAPEC-G机制的收益对比结果，可知在用户数量较大(大于500)时，VMAPEC-OPT会产生更大收益，这与VMAPEC-OPT机制的资源分配算法是最优算法有关，但VMAPEC-G机制仍然能达到最优结果的90%以上；而在用户量较小(200个用户)时，VMAPEC-G和VMAPEC-OPT的结果相差不大，因为较小用户量时资源竞争也相对较小。

Figure 3 Comparison results of revenue图3 收益对比结果

图4显示了VMAPEC-OPT和VMAPEC-G机制的收益计算对数时间对比结果，可明显看出VMAPEC-G机制的收益计算时间远小于VMAPEC-OPT机制的，约小于VMAPEC-OPT机制的1%。因为支付价格的计算需要先进行资源分配，同时支付算法还需要不断迭代计算资源分配情况，造成收益计算时间远大于资源分配时间，相比之下，VMAPEC-OPT机制的高时耗的资源分配算法会严重影响收益计算时间，这使得VMAPEC-G机制相比VMAPEC-OPT机制拥有更好的可行性。

Figure 4 Comparison results of revenue calculation time图4 收益计算时间对比结果

4.2.3 资源利用率

资源利用率是拍卖获胜用户的资源需求总和占资源提供商对应类型资源容量总和的百分比，可由资源分配的结果计算得出。资源利用率对资源分配算法的衡量具有一定参考。

图5～图7分别显示了3种拍卖机制的CPU、内存和磁盘的利用率。从图5～图7可以看出，3种拍卖机制的资源利用率总体较为接近，表明VMAPEC-G和G-VMPAC-II机制与最优机制一样均趋向于使资源耗尽，这表明2种贪婪机制也能够比较充分地利用资源。从图7还可以发现，3种机制的磁盘利用率相对较小，但这和各虚拟机的配置和资源提供商的资源容量配置有关，这也可以给资源提供商进行实际的资源配置时提供一定参考。

Figure 5 Comparison results of CPU utilization图5 CPU利用率对比结果

Figure 6 Comparison results of memory utilization图6 内存利用率对比结果

Figure 7 Comparison results of disk utilization图7 磁盘利用率对比结果

5 结束语

本文研究了边缘计算环境下的资源分配问题，并对该问题进行了数学建模，提出了VMAPEC-OPT和VMAPEC-G 2种拍卖机制，并从理论上证明了这2种拍卖机制是防策略的。同时，通过实验结果分析可以看出，VMAPEC-G机制在社会福利、资源分配时间、收益、收益计算时间和资源利用率等多方面都能取得不错的效果，表明VMAPEC-G机制在边缘计算系统的资源分配问题中具有良好的有效性和可行性。

在下一步工作中，拟考虑用户资源需求的动态性，引入时间尺度，用户的资源需求可以在不同时刻动态产生，以增强机制的实用性。