基于GeoGebra的高中数学课题教学研究

吴国强

摘要：为了能够有效提升GeoGebra的高中数学课题教学实效性，本文通过具体论述GeoGebra的高中数学课题教学策略，为增强高中学生的数学素养提供可参考的资料。

关键词：GeoGebra;高中数学;课题

GeoGebra界面中包含了诸多的基本元素，如向量、角、函数、直线、点等。当然，也正是基于众多元素的不同组合与排布，方使得图像也具备了“动态化”的特征，继而可将原本枯燥、抽象的内容生成过程以直观化的形式进行呈现。这将进一步增添图像的可观性。不仅如此，GeoGebra中还内置了非常多的属性，除了最为常用的几何属性外，指令区中包含的各类属性也具备了众多的功能。诸如计算圆锥的曲线、正多边形、切线、函数、离散、统计以及列表等。除此之外，GeoGebra上的多元化属性还能让图形呈现出更佳的视觉效果，如针对文本格式的调试、对颜色、位置的掌控以及样式等。至于GeoGebra作图则有两种最为常见的应用方式，分别为“尺规作图”与“代数输入”。其中，“尺规作图”主要运用了绘图工具中包含的各类作图基本元素。如多边形、滑竿、点、直线等。而代数输入则是利用了函数方程式，通过将函数方程输入到指令区域内边疆得到相应的函数图像。

一、多角度揭示概念內涵，合理进入课堂教学

基于数学概念本身具有的多元、多样、复杂、抽象等特征，故在揭示其内涵时亦当基于不同的背景、层次以及结构等众多角度进行。如此方能让学生对概念产生一个较为完整的认知。诸如针对“函数概念”的相关内容教学，借助GeoGebra则相关函数概念的刻画则可由解析式、图像及表格三方面结构切入。

首先，指导学生参与策略。相较于教师的传输与交到，学生通过自身的摸索或是直接操作相关模型，势必更能掌握其中概念。因此，针对概念部分的具体教学，教师需将第一要务放到激发学生学习的主观能动性之上，以此为学生探索概念本质属性提供一个良好平台并进一步提升学生的课堂参与度。

其次，形成概念体系。针对概念的学习并不能将之作为独立章节，原因便在于众多概念的形式过程本身便有着极为密切的关联。

二、优化教学过程，锻炼学生数学思维

基于GeoGebra的高中数学课题教学时，应该优化教学过程，注重学生的数学思维锻炼。例如，以椭圆的标准方程这节内容为例进行分析：

对于“椭圆”章节的具体教学，教师的主要教学目标有如下几方面：一是椭圆的定义;二是坐标系的建立;三是椭圆标准方程。当然，该过程教师可使用GeoGebra来为学生展示相应模型，随后一步步指引学生去总结椭圆定义。在探索出椭圆定义后，教师同样可基于GeoGebra来推导椭圆的标准方程。如此一来，学生不仅能学习到相关知识，同时也能强化他们发现与总结规律的能力，继而逐步形成严谨的数学思维。

除了上述教学方法外，教师亦可采取学生合作学习的方式，以此还能同步培养学生的合作交流能力，这对学生今后的学习及发展均有较大助益。

教学难点：推导椭圆标准方程

教学过程：首先，创设情境、导入新课利用 PPT 投影仪展示生活中常见的椭圆形建筑物，并提出问题.如图2：

问题：PPT上显示为何种图形？还有哪些事物与之相似呢？

预设学生活动：椭圆、盘子、篮球投影等。

在学生举例后，教师又可为学生讲述与该知识相关的故事。如针对圆锥曲线的教学，教师便可为学生讲述古希腊时代人们运用平面切割圆锥的方式获得曲线的事例并借助GeoGebra来加以战士。如此学生势必能快速找准本章节的学习重点并形成完整的知识体系。

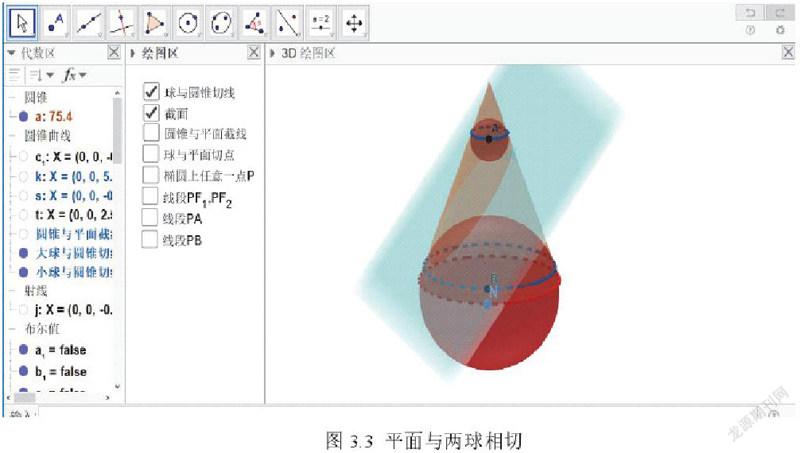
教师向学生展示书上阅读内容里的数学科学家 Germinal Dandelin 从纯几何的角度证明平面截圆锥是一个椭圆.在圆锥里放置两个球，一平面与两球相切，如图3所示：

让学生回顾本节课学历哪些知识点，并强调要注意双曲线定义的重点以及与椭圆的区别。

就传统教学而言，针对双曲线定义部分的具体教学往往仅是基于拉链的开合，随后的双曲线定义、焦点、焦距等内容同样基于此。这不仅让教学过程显得过于简易且并不能让学生体会知识的形成过程，继而也很难对学生思维产生有效培养。因此，为规避以上教学避免。教师可充分利用GeoGebra来为学生详尽呈现双曲线相关知识的形成过程，如此一来，学生在建构知识轮廓时势必更为完整，继而也能深化学生对知识的记忆与理解。

总之，将GeoGebra引进高中数学教学不仅能帮助学生更好地理解数学知识、概念、定义等极具抽象性的内容，同时还能有效激发学生的学习兴趣。因此，教师亦当对GeoGebra的引进给予高度重视，继而在保证良好的教学效率同时亦为学生今后的学习及发展奠定牢固基础。

参考文献：

[1]张志勇. GeoGebra软件在高中数学教学中的应用举例[J].福建中学数学，2014（4）：6-9.

[2]寇恒清. GeoGebra在高中数学教学中的应用初探[J].数学通报，2015（9）：48-51.