基于整数规划的营养配餐决策优化研究

史节

摘要：本文對营养配餐决策优化问题进行研究，建立多类菜品选择下的整数规划的0-1规划模型，以广州工商学院第三食堂大众餐饮的营养配餐购买决策优化为例，建立0-1整数规划模型，并利用Microsoft Excel进行求解，求解结果可以有效实现在满足基本营养和口味丰富化的需求前提下，费用成本最小化的目标。

关键词：营养配餐：0-1整数规划;决策模型

一、绪论

在人类的整个生命周期中，膳食是维持人体生长发育和健康至关重要的因素，长期均衡而合理的膳食是实现全面、均衡营养的基础和保障。它能维护和促进人体健康，提高机体免疫能力。而大学生尚处于身体的成长发育阶段，兼之有丰富的校园活动和学习任务，营养配餐可为其提供合适的膳食，提高学生的学习和工作效率。

而从《国民营养计划（2017-2030年）》、《健康中国行动（2019-2030年）》[1]、《“健康中国2030”规划纲要》等最近发布的权威文件中，我们可以看到如今正是是我国改善国民营养健康、降低疾病负担的关键战略期，作为新时代新青年，我们应积极响应政府号召，提高自身身体素质，可以从注意生活中的饮食开始做起。

二、研究综述

在查阅寻找相关营养膳食文献资料的过程中，我们对在营养配餐方面的一些具代表性的学者研究方向和观点作出了整理。

潘敏[2]认为一般大学生没有收入，在就餐时会考虑到饮食成本的问题，才用了线性规划模型，以满足营养和热量为条件前提，对大学生实现经济营养配餐做出了研究。

马立新[3]以配餐营养、配餐成本的降低为目标，提出了营养的优化问题，并建立了相关线性规划模型，同时对相关食品的物价如何进行预测和模型建立。

崔京进[4]认为营养配餐是一种蕴涵了多学科知识的崭新的餐饮模式，他对餐饮业经营者如何进行合理的营养配餐，从营养食谱的确定、岗位操作工艺等角度进行研究与阐述。

廖晓寰、张羽、梁少萍、高青、郑泓[5]通过问卷方式，联合对广东省的高校学生一周内的用餐情况进行调查分析，发现广东省高校大学生存在膳食结构不合理的情况，对此推出了五套营养配餐方案。

目前，在营养配餐领域，还没有出现研究机构专门对大学生这一群体的营养状况进行深入的调查分析。此外，国内在营养配餐的优化问题研究成果不够丰富，其多数文献资料的内容主要是模型的假设上，实际的举例不多。

而在本文，作者在建立模型后，以广州工商学院三水校区大众食堂为具体对象，进行了相关膳食的调查。调查分析结果可为本校学生提供营养配餐优化的思路，也可为食堂的经营者供应什么菜品提供参考。

三、模型构建

学生进行饮食决策的过程中受到多方面因素的影响，包括：菜品价格、菜品种类、就餐便利性、营养需求等因素。那么如何对这些菜品进行抉择，才能满足学生的最低营养需求前提下，使得饮食成本最小化呢？

为深入地对大学生饮食成本最小化的问题进行研究，进一步建立优化模型，我们将基于成本最小化原则，以满足学生的基本营养需求为驱动因素，构建学生营养配餐决策的优化模型。学生使用该模型进行配餐决策，可以改善自身营养状况，缩减饮食费用，同时提高自身的健康意识和理财意识。

（一）营养配餐问题的适用模型

整数规划是要求全部或部分决策变量为非负整数值的一种线性规划类型，常用于设备的购买、投入的车辆数等需要取非负整数的决策问题中。

整数规划一般可以分为一般整数规划和0-1整数规划两大类，在此我们主要运用0-1规划。0-l规划属于整数规划的特殊情况，它的决策变量取值仅可为0或1，适用于我们进行高校学生一天中午餐最优决策的问题研究。

为了进行科学准确的评价方案选择，我们进行了必要的假设条件的设定。

（二）0-1整数规划模型的建立

假设食堂提供n种饭菜，一个餐盘容量可装x份菜。学生以选择的菜品满足营养和口味丰富化为前提，进行一天午餐和晚餐的规划，尽可能使饮食费用花费最少，由此建立模型。

1.决策变量

设变量Xi（其中，i=1，2，3…N）以表示每个菜品的分别购买份数。

2.目标函数

以午餐与中餐一共花费的最小成本z作为目标函数，则目标函数为：minz=

其中，CL以表示每个菜品的单价（单位：元/份）。

3.约束条件

①Aw<=<=Bf 即购买的各饭菜中的相同营养素的含量之和受人体的营养需求量范围限制。其中，YJ代表饭菜中不同营养素的相应含量，Xi代表各类饭菜的对应购买份数，Aw，Bf 表示人体中晚两餐对不同营养素的需求量。

②D<=<=E，即学生中餐与晚餐所选择购买的菜品份数在D份到E份之间;

③Xi=0，1，即各菜品的购买份数只能取整，且取值“0”或“1”。

由得到该决策的整数线性规划模型为：

四、实例分析

广州工商学院三水校区的一位大三学生准备提前进行第二天的中、晚餐的饮食规划，初步确定在第三食堂大众餐饮就餐。在校园外卖购微信小程序了解饭堂提供的菜品信息后，该学生准备应用上述整数模型以优化饮食决策，他希望一天饮食的总和能满足基本营养需求，且饮食费用能最小化。

（一）配餐决策的条件

1.客观条件

经实地调查，结合中国营养学会中国营养学会制定的《中国居民膳食营养素参考摄入量》、中国营养学会理事长杨月欣与王光亚、潘兴昌主编的《中国食物成分表》等相关营养文献资料，我们得到第三食堂大众餐饮常供菜品的种类、价格以及对应的人体必要的营养素含量，相关数据如下表4-1，表4-2所示。

在表4-1中，菜品每份100g，营养元素含量以每100g计。

2.主观条件

（1）出于营养和口味丰富化的考虑，学生购买午餐或晚餐时，设定一餐的购买的菜肴份数不低于2份，一种菜肴最多点一份或者不点。

（2）为尽量避免粮食浪费，学生购买午餐或晚餐时，设定一餐的菜肴份数最高不超过3份，每份菜的单位规格以100g/份计。

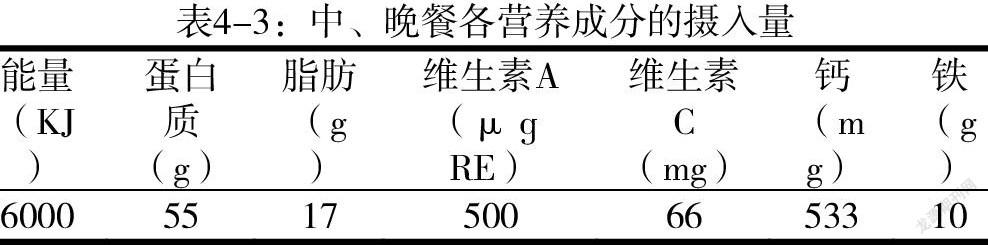
（3）该学生的体重目标为保持，中餐和晚餐的营养成分摄入量为每日膳食营养素参考摄入量的2/3。该学生结合自身情况计划出中晚餐的各营养成分的基本摄入量，如表4-3所示。此外，他计划中、晚餐摄入的能量之和不超过7000KJ。

（二）配餐决策模型求解

由上述条件，利用整数线性规划寻找饮食费用最小化的方案，建立数学模型如下：

Minz=2x1+2x2+1.5x3+3.5x4+3.5x5+3.5x6+3x7+3x8+3x9+6x10+6x11+5x12+5x13

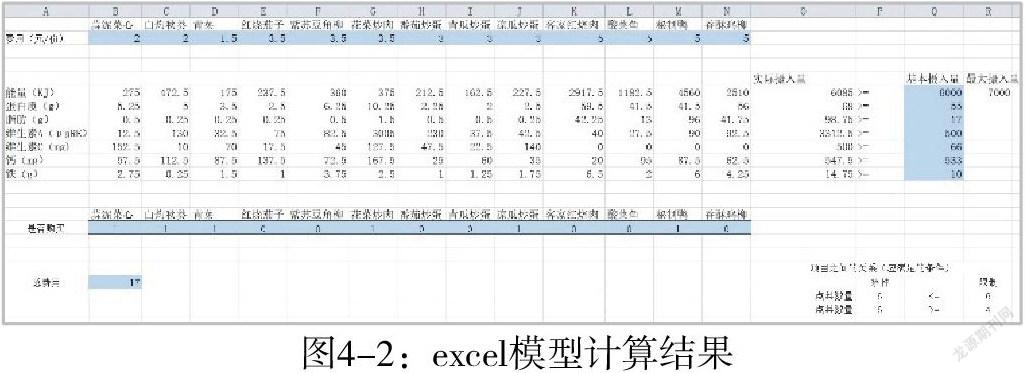
把该线性规划数学模型代入microsoft excel 软件中，采用线性规划方法进行求解，约束条件与计算结果如图4-1、图4-2所示：

由图，我们可以看到，午餐和晚餐总共选择菜品蒜泥菜心、白灼秋葵、青菜、花菜炒肉、凉瓜炒蛋、秘制鸭六道菜为饮食最优决策，此时营养成分摄入达到需求，饮食总费用为17元。学生可以将其按自己的偏好分成两部分点餐，比如，午餐点蒜泥菜心、青菜、秘制鸭，晚餐点白灼秋葵、花菜炒肉、凉瓜炒蛋。

五、结论

在本文中我们采用0-1整数规划法，建立饮食决策数学模型，并以广州工商学院三水校区第三食堂大众餐饮为例，对学生拟点午餐和晚餐的菜品购买决策进行了优化计算，从而得出中、晚餐可以选择购买的菜品和相关营养成分的实际摄入量以及饮食的总费用。我们基于整数规划模型的配餐决策研究为高校大学生如何进行合理的饮食决策提供了一个参考思路。此外，在我们的生活中，这类整数模型可以作为一个简单实用快捷的决策工具应用，解决其他领域的问题，比如工作人员的指派、物流运输网络选址、水资源配置等。我们此次的研究有一些不足的地方，比如，在建立此饮食决策模型时，为了突出问题重点以及让模型应用能更具体化，我们对菜品的种类、份数等一些条件进行了约束;再加之在购买菜品进行调查时，没有充足的工具对食品相关营养成分进行精确检测，这使得在实际生活中我们建立的该模型在计算结果上可能有一定的偏差。欢迎各界有识之士与我们一起探讨模型的进一步改善，让模型计算结果更具有可操作性，更贴合实际。

参考文献：

[1]健康中国行动（2019—2030年）：总体要求、重大行动及主要指标[J].中国循环杂志，2019，34（09）：846-858.

[2]潘敏.經济营养配餐的线性规划模型[J].食品界，2017（09）：80.

[3]马立新.优化理论在营养配餐问题中的应用[J].科技信息，2007（07）：164.

[4]崔京进.餐饮业中的营养配餐[J].中国食品，2004（03）：30-31.

[5]廖晓寰，张羽，梁少萍，高青，郑泓，梁惠仪，李彦奇.广东省高校大学生膳食调查及营养配餐推荐[J].广东微量元素科学，2003（08）：24-41.