快速傅里叶变换在信号处理中的应用

於 玺

（同济大学浙江学院 浙江 嘉兴 314000）

1 引言

傅里叶变换在信息学科拥有很高地位。但计算机只能处理离散且有限长序列，因此它在离散域中的表达形式—离散傅里叶变换（discrete fourier transform，DFT）产生了。离散傅里叶变换可以直接用来进行计算分析工作，因此在数字信号处理中，常常会用到此方法来分析信号频谱、计算频率响应等。1965年，快速傅里叶变换算法（fast fourier transform，FFT）首次被提出。在对速度要求没有非常高的情形下，FFT基本上可以满足工业应用的要求。在处理数字信号时，常常可以用离散傅里叶变换来实现它的运算，所以快速傅里叶变换算法之于数字信号处理具有不可替代的作用。因此，在快速傅里叶变换诞生之后，数字信号处理技术的发展越加迅速、应用范围也越加广泛，几乎渗透进了社会生产和生活的方方面面。

2 国内研究现状

张玲佳[1]在对FFT算法的原理及FFT硬件加速器的影响因素进行研究之后，对高维度FFT加速器进行了设计及硬件实现。在雷达信号处理领域，为实现动目标检测技术，谢辉辉[2]设计了一种可变点和一种定点FFT处理器。在图像融合领域，曹端良[3]提出一种改进的HIS+SWT算法，此外，还提出一种改进的快速傅里叶变换的泊松图像融合算法。在频谱分析方面，邢鑫[4]对基于FFT的频谱细化算法进行了深入研究。在电力系统下，为减少谐波污染问题，张旭东[5]基于FFT的谐波检测算法提出加6项组合余弦窗双谱线插值修正谐波检测算法。黄纯等[6]提出分通道分时段压缩方案，以减少电力系统中大量故障数据的传输问题。在对色谱噪声进行平滑方面，杨黎等[7]将FFT法与其他数字滤波法进行比较后发现，FFT法能更好进行噪声平滑处理，并使信噪比提高18倍。在对图像中的噪声进行平滑方面，林志斌等[8]提出一种新的基于OGSTV的图像去噪方法，该法加入了FFT理论后，大大缩短了去噪时间。此外，陆文祺[9]深入研究了基于高阶模型的图像去噪，此外对其快速算法进行了分析。在轨道电路移频信号检测上，安义岩[10]提出基于带通采样的FFT轨道移频信号调解算法以提高解调精确度。

3 快速傅里叶变换FFT原理及其优越性

3.1 快速傅里叶变换FFT原理

模拟信号x（t）连续傅里叶变换：

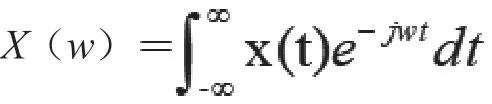
x（t）T个抽样周期后变为x（nT）。设x（n）为N点有限长序列。

其DFT为：

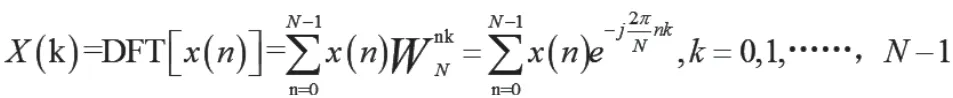
由上式可见，接下来运算十分复杂。

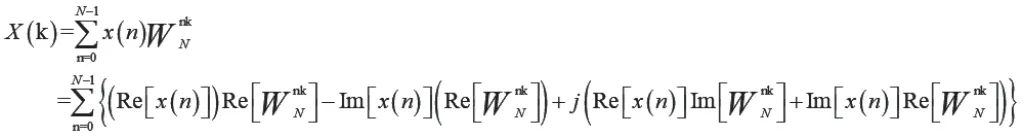
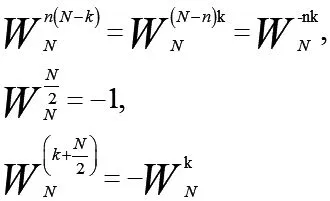
3.2 快速傅里叶变换的优越性

计算的工作常常通过计算机来进行。在使用傅里叶变换进行复杂运算时，计算机往往会因为运算负担过大而导致高耗电量。因此，运算速度相对较慢的计算机系统常常对此敬而远之。而由于快速傅里叶变换对运算的低要求及其运算快的优点，使得FFT在生产和生活中作用都极其巨大。

4 快速傅里叶变换在信号处理中的应用

信号处理，简言之，就是人们为了得到有用信息，而对原信号进行一系列处理的方式。以下是对FFT在信号处理中的应用进行的分析与总结。

4.1 用FFT进行离散信号压缩

FFT算法压缩比高，因而可以用其进行信号压缩。快速傅里叶变换可以在某个给定的错误容限下，把小于相应阈值的快速傅里叶变换系数置零，从而减少需要传输的系数，最后实现压缩。例如，大量故障录波数据常会出现在电力系统中。庞大数量的故障录波数据会使得之后存储和实时传输故障信号会变得十分困难，而压缩录波数据的方法可以大大改善这一问题。

4.2 用FFT实现快速卷积

卷积在分析数学中有重要作用，常被用来进行信号分析。如果f（x）、g（x）为 (实数集)上两个可积函数，对其作积分：

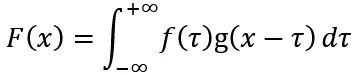
则称F(x)为函数f（x）、g（x）的卷积。常表示为F（x）=f（x）*g（x）。

对于定义在 Z（整数集）上的函数f 、g，卷积定义为：

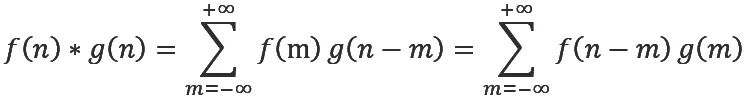
卷积定理：如果两个时间序列h（k）和x（k）分别为 H（m）和X（m），那么h（k）*x（k）的DFT为H（m）点乘X（m），H（m）点乘X（m）的IDFT为h（k）*x（k）。应用快速傅里叶变换实现快速卷积，简言之，是将N点的DFT不断等分到很小，计算2点、4点或混合基的DFT，此法能使DFT的计算难度降低。

4.3 用FFT进行谐波检测

随着经济的迅猛发展、各类电力电子设备的广泛使用，电力系统的污染比如谐波问题也日渐严重。快速傅里叶变换常常被用来检测基波和整数次谐波，从而进行谐波检测。

尽管基于FFT的谐波检测算法应用范围广，但其也存在局限，比如FFT法存在较大误差。此外，FFT法还需一定时间进行采样。为了使FFT法的计算准确率和计算速度有所提升，目前，改进方法有加窗插值算法、双峰谱线修正算法和组合方法。此外，针对此法的局限性，许多学者提出了许多能够起到明显效果的小策略，如张旭东[5]提出的优化算法。

4.4 用FFT进行去噪

在各领域进行信号检测，都会产生一定噪声信号，以下以色谱、图像两方面的信号去噪为例。

色谱数字信号除了包含检测器对所分析的样品产生的响应信号，还包含整个系统带来的噪声信号，这使得色谱峰的检测、判别与数据处理变得困难。在对色谱信号进行去噪方面，使用快速傅里叶变换能大大缩短检测时间、提高检测灵敏度。

在图像去噪方面，由于图像常会产生不同的噪声，为了得到清晰优质的图像，我们需要在图像处理之前对其进行去噪处理，使用FFT对其在频域进行操作是一种有效的方式。将图像进行傅里叶变换使其转化到频域，我们可以将得到的图像像素中高频部分的幅值置为0，同时只保留低频部分幅值，图像噪声从而得以简单去除，使得图像得到一定平滑，但此法未能精确去除噪声。因此，也产生了许多基于FFT的新算法，如林志斌[8]在传统OGSTV的图像去噪方法中引入了FFT，使得图像去噪时间大大缩减。

4.5 关于FFT的硬件实现

在合理利用硬件特性的基础上，硬件加速器能够使计算更为快速。而硬件本身存在一定的局限性，如内存、成本等方面。因此许多学者针对这一局限，提出了自己的想法，如张玲佳[1]在文献中提出了一种高速、低资源消耗的变维度FFT硬件加速器。这种硬件加速器可以很好地适应复杂数字信号处理对不同维度、不同点数的快速傅里叶变换计算任务。

4.6 用FFT进行信号检测

雷达探测的环境中通常都充斥着各种杂波，进而干扰雷达探测到的结果。因此我们需要通过动目标检测以滤除干扰项、保留运动目标的回波。在雷达信号领域，FFT常用于滤波。由文献[2]动目标检测常使用多普勒滤波器组FIR横向数字滤波器进行滤波。为了提高运算效率、简化实现过程，快速傅里叶变换算法大大降低运算要求，同时大大缩小了所需硬件面积。而此法在检测性能上有局限性，因此常常将其与MTI配合使用。此外，FFT滤波器组在灵活性、抑制杂波能力等方面也有一定局限，在这些方面仍需深入研究。

在轨道交通领域，常需要检测列控系统中的移频信号，以判断轨道区段是否占用，从而防止错误办理。然而，轨道电路中的信号检测常受到牵引电流和相邻轨道区段的移频信号的影响。因此，想对其进行信号检测，首先需要进行信号解调，使用FFT算法的频域检测法目前常用于信号解调。目前，许多学者在此基础上对移频信号检测技术进行了优化，如安义岩[10]提出基于带通采样的FFT轨道移频信号调解算法，使解调精确度进一步提高。

5 结语

本文对快速傅里叶变换算法进行了分析，并详述了FFT在信号处理中的应用。快速傅里叶变换运算高效便捷，为信号处理提供了良好的条件。