我国体育院校发展的预测模型建立

林子淇，李明俊,曹秀玲

(1.山东体育学院 研究生教育学院， 济南 250102; 2.北京工业职业技术学院,北京100042; 3.湖北第二师范学院 体育学院, 武汉430205)

在我国高等教育快速发展的背景下，我国体育院校也随之迅猛地发展。那么，体育院校的发展情况如何，发展趋势怎样，这些都成为研究体育院校发展的关键性问题。本研究以体育院校生态的模糊综合评价指标值为对象，应用趋势外推预测模型、指数平滑预测模型、非平稳时间序列预测模型三种重要的预测方法，来推断我国体育院校的未来发展趋势。

1 预测模型的构建思想

我国体育院校(系)专业在必修与选修、学科与术科、限选课与任选课，开课门数等方面进行过多次调整，本研究以1997年后我国体育院校(系)数量增长情况、国家社会科学基金体育学课题立项情况和国家社科基金立项课题成果形式，由模糊综合评价方法，利用SPSS软件计算得出可以用来衡量体育院校生态优劣程度的一个综合评价指标(F)，从1997年至2019年的每一年都与一个综合评价指标值相对应，也可以称之为综合评价指数。本研究的目标是构建出一个综合评价指标综合值的预测模型，对2020年之后的F值做出相应的预测。

为了提高最终构造的预测模型的准确性，研究采取以下的建模步骤来建立综合评价指标的预测模型：

第一步，采用1997-2012年的数据初步建立一个预测模型A；

第二步，通过2013-2015年的真实值与预测值的比较来检验模型A的精确性；

第三步，模型A的稳定性得以确定后，将2013-2015年的数据也用于建模，重新构建一个预测模型B；

第四步，由模型B对2016-2020年的综合评价指数进行预测。

为了进一步提高模型的精确性，在建立模型A和模型B时，研究采取如下的方法：

第一，采用单个模型进行预测，具体有趋势外推预测模型，指数平滑预测模型，时间序列模型。

第二，将单个模型预测值取不同的权重进行组合预测，所得出的预测值作为预测的最终结果。

2 单个预测模型的初步建立

2.1 趋势外推预测模型

2.1.1 模型介绍

统计资料表明，以时间为自变量，预测依时间变化呈现出某种上升或下降的趋势，建立趋势模型：

y=f(t)

在实际应用中，需要给予变量所需要的值，这样就能够得到未来的时间序列值，即趋势外推法。

2.1.2 数据分析

根据《普通高等学校本科专业目录》和已收集到的数据，由模糊综合评价方法，利用SPSS软件计算出1997-2019年的综合评价指标。

运用SPSS软件，根据数据建立趋势模型，为了判断模型的趋势，研究中先画出原始值的趋势图，发现趋势图显示明显的非线性的特征，为了确定模型的方程，对其拟合不同曲线，与观测值进行比较，选择最优的拟合模型。

A．拟合线性模型(图1)

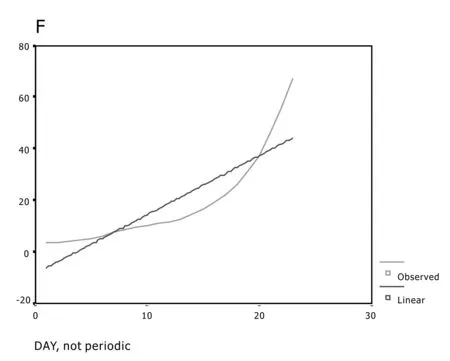
图1 拟合线性模型

B．拟合二次曲线(图2)

图2 拟合二次曲线

C．拟合三次曲线(图3)

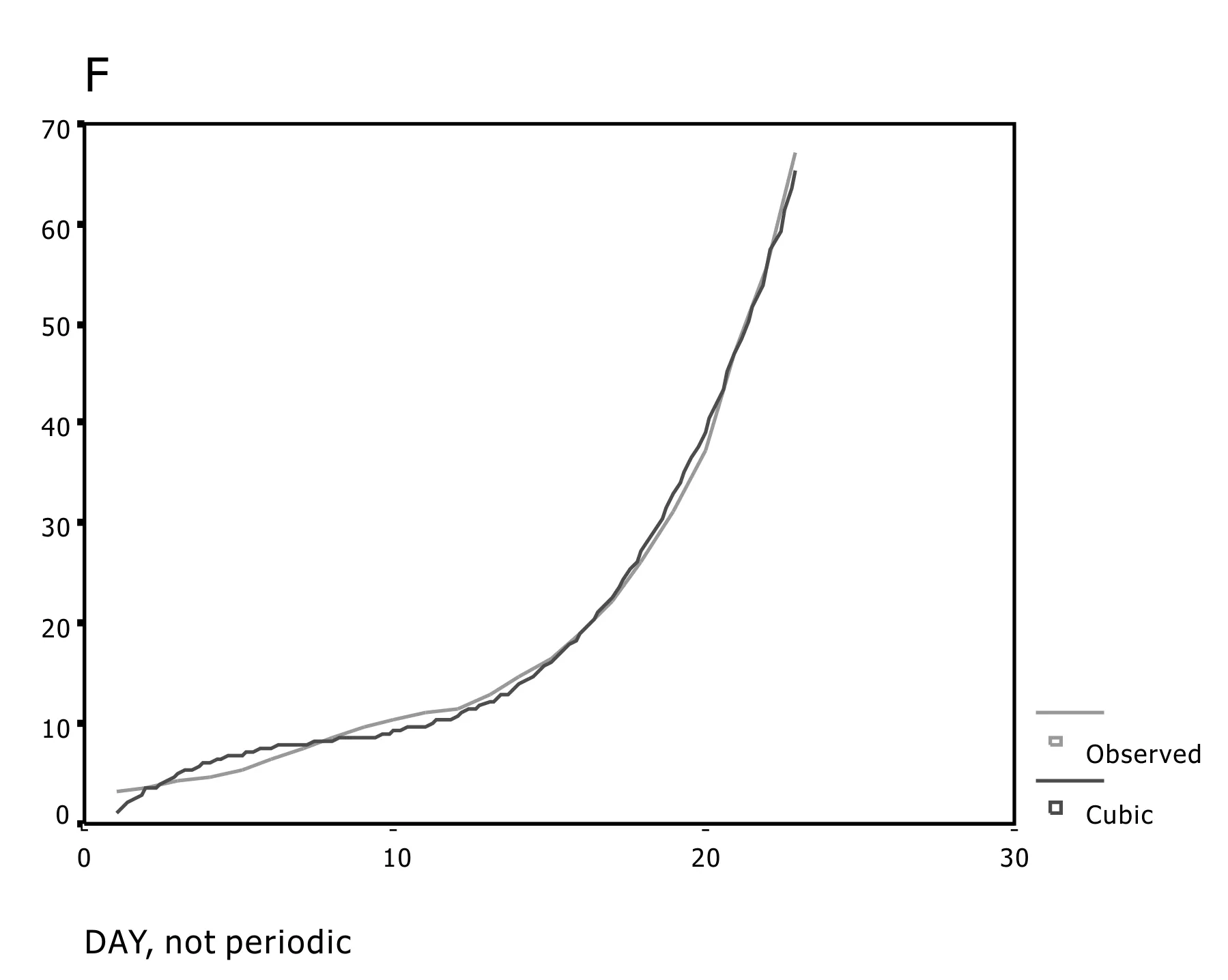
图3 拟合三次曲线

D．拟合指数曲线(图4)

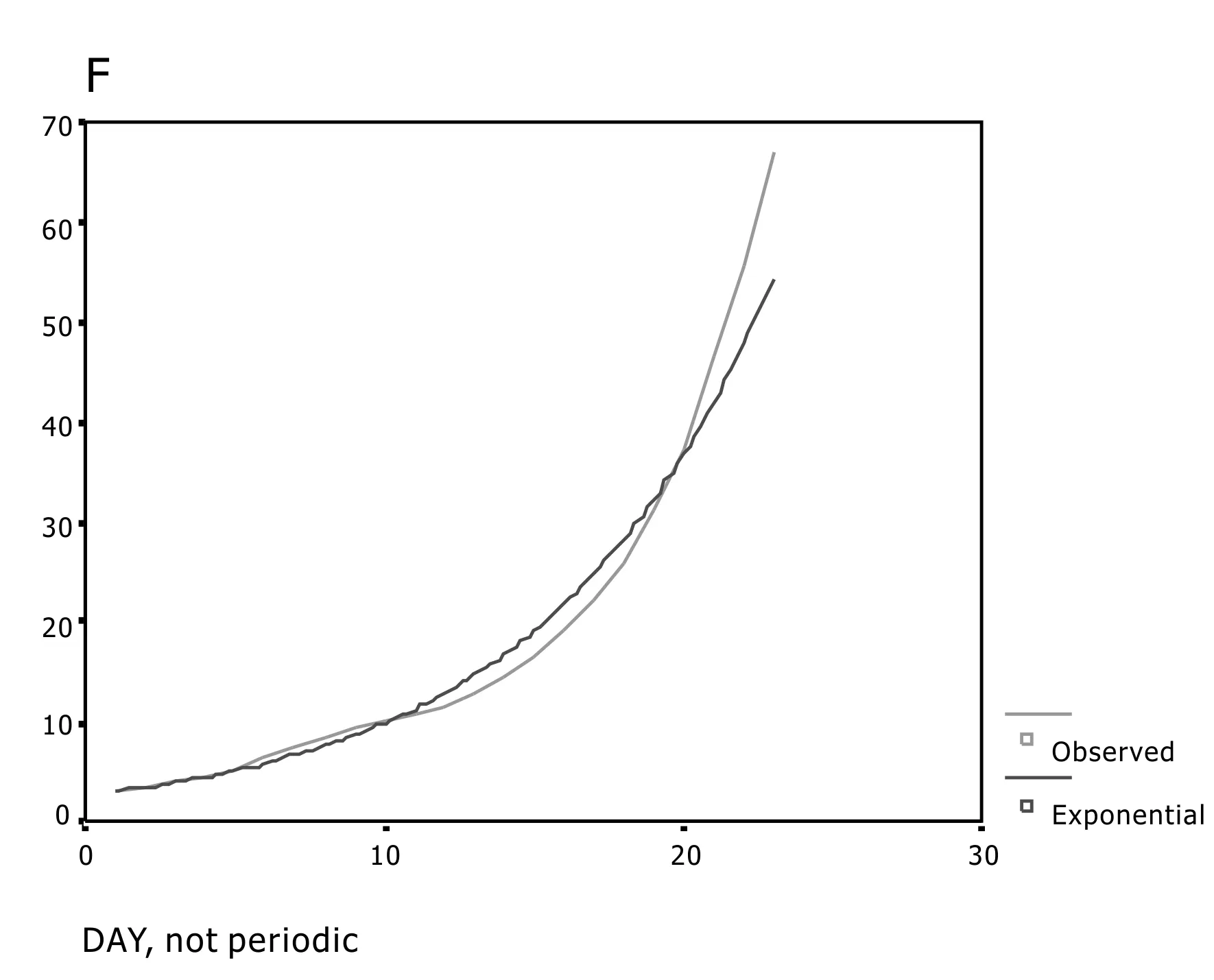
图4 拟合指数曲线

观察以上各图可以得出用三次曲线对模型进行拟合效果最好，下面继续用SPSS软件对数据进行三次曲线的拟合。拟合的模型为：

F=B0+B1X+B2X2+B3X3

其中F为综合评价指标值，X为序号(X=1，2，…23),B0,B1,B2,B3为参数。

SPSS软件运行的结果如下：

由输出结果得到的拟合方程为：

F =-1.748844306+3.131597795X+

-0.355581331X2+0.015064606X3

在汇总的信息中，显示了R2为0.99563，表明拟合方程显著有效。

做出拟合曲线与观测值比较的预测效果图，如图5：

图5 拟合3次方曲线的预测效果图

通过上面显著性检验以及拟合曲线与散点图的比较可以得知，模型的拟合是显著的。

由回归方程可以预测得到后三年(2013-2015年)的F值，另记为F1，见表2。

表2 用趋势外推模型预测的综合评价指标值(2013-2015年)

2.2 指数平滑预测模型

2.2.1 模型介绍

作为进行趋势分析和预测常用的指数平滑法，其基本思想是考虑时间间隔对事件发展的影响，各期权重随时间间隔的增大而呈指数衰减。

由趋势图原始值中可知本文所要研究的综合评价指标的时间序列数据含有线性递增的趋势，因此考虑采用霍尔特(Holt)双参数线性指数平滑的方法进行分析和拟合。

霍尔特(Holt)双参数线性指数平滑是分别对原时间序列及时间序列的趋势进行平滑。它的具体模型如下：

St=αYt+(1-α)(St-1+bt-1)

3-2-1

bt=γ(St-1-St-1)+(1-γ)bt-1

3-2-2

Ft+m=St+bt·m

3-3-3

其中：

α为水平平滑系数；S1为t时期的平滑值；γ为趋势平滑系数；

bt为t时期的趋势平滑值；m为预测长度。

2.2.2 数据分析

采用SPSS软件拟合霍尔特(Holt)双参数线性指数平滑模型，输出结果如下：

由以上输出结果可得两参数为α=0.9,γ=1

做出拟合曲线与观测值比较的预测效果，从拟合指数平滑曲线的预测效果可以看出，霍尔特(Holt)双参数线性指数平滑模型拟合良好。

下面对2013-2015年的F值做出预测，另记为F2，见表3：

表3 用指数平滑模型预测的综合评价指标值(2013-2015年)

2.3 非平稳时间序列预测模型

2.3.1 模型介绍

具有如下结构的模型称为求和自回归移动平均(autoregressive integrated moving average)模型，简记为ARIMA(p,d,q)模型：

(*)

式中：▽d=(1-B)d

φ(B)=1-φ1B-…-φpBp,为平稳可逆ARMA(p,q)模型的自回归系数多项式

Θ(B)=1-θ1B-…-θqBq,为平稳可逆ARMA(p,q)模型的移动平滑系数多项式

(*)式可以简记为：

(**)

式中，{εt}为零均值白噪声序列。

ARIMA(p,d,q)模型的实质就是差分运算与ARMA(p,q)模型的组合。任何非平稳序列只要通过适当阶数的差分实现差分后平稳，就可以对差分后序列进行ARMA模型拟合了。

2.3.2数据分析

利用SAS软件上机编程对1997-2019年综合评价指标评价值(见表1)建模，具体步骤如下：首先绘制时序图，然后对模型进行检验，输出结果如下：

表1 1997-2019年体育院校的综合评价指标值

参数显著性检验结果显示两参数均高度显著。做出拟合曲线与观测值比较的预测效果，并且看出ARIMA模型拟合良好。

下面对序列作为期3年的预测。对F的预测值另记为F3，见表4：

表4 用ARIMA模型预测的综合评价指标值(2013-2015年)

3 组合预测模型的初步建立

3.1 组合预测模型

3.1.1 模型介绍

研究表明，因组合预测模型能获得更好的预测值，所以比单一预测模型更具优势。

具有如下形式的组合模型称为线性组合模型：

y0t=W1y1t+W2y2t+…+Wnynt

其中Y0t为t期的组合预测值；

y1t,y2t,…ynt为n种不同单项预测模型在t期的预测值；

W1,W2,…Wn为相应的 n 种组合权数。

线性组合预测模型的关键在于确定合理的权数Wi，Wi依据组合预测误差的方差最小原则加以确定。

最优线性组合模型是线性组合模型中的一种，它的原理是：利用样本期的实际值和各单项预测模型的拟合值，进行线性回归，然后利用线性回归模型，以原方案的预测值作为外生变量进行外推预测。

最优线性组合模型的一般形式为：

yt=a+b1y1t+…+bnynt

其中为样本期实际值；

y1t…ynt,为样本期n个不同模型得到的预测值；

3.1.2 数据分析

利用SAS软件的INSIGHT模块进行最优线性组合模型拟合。将1997-2019年体育生态综合评价指标实际值(F)作为因变量，趋势外推预测模型、指数平滑预测模型和时间序列预测模型这三个单一模型对F的预测的结果(F1，F2，F3)作为自变量，进行多元线性回归拟合，具体数据见附表5。上机输出的结果如下：

输出结果显示，拟合的方程各方面的都是显著的。由回归方程：

F=0.1883F1+0.5379F2+0.2958F3

可以对2013-2015年的体育院校生态综合评价指数水平值(F)进行预测，预测结果见表5：

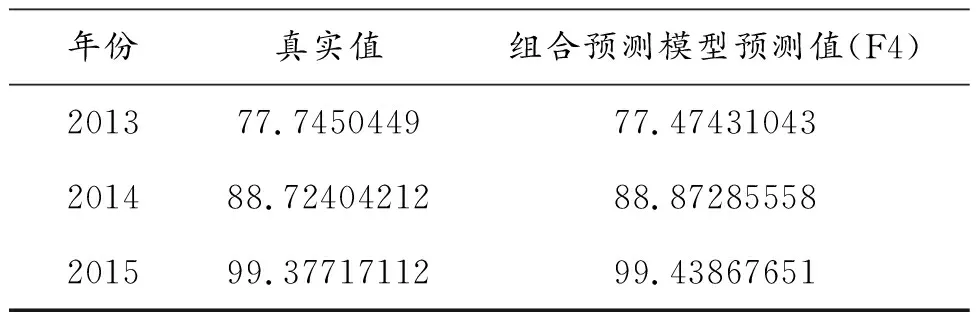
表5 用组合预测模型预测的综合评价指标值(2013-2015年)

3.2 组合预测模型的精确性检验

本研究首先采用了三种单一的预测模型，对2013-2015年的体育院校生态综合评价指数值进行了预测。虽然每种模型都有各自不同的特点，但是组合预测将各种预测效果进行总体性综合考虑，比单个模型更系统、更全面。

下面通过对各个单一模型的预测误差的绝对值来比较各个模型的预测精度。从表6可以看出，组合预测模型的预测误差要远远小于单一模型的预测误差。

表6 各模型预测精度的比较

做出组合预测与真实值比较的预测效果，研究显示预测值与真实值拟合的非常好。

4 模型的最终建立

通过前面的结果证明了应用三种单项预测，可以组合出优于每个单项的预测结果，能进一步有效提高预测精度，因此本研究继续使用如上的组合预测模型的构建方法，对全部数据进行建模，并对未知的2016-2020年的综合评价指标值做出预测。

使用1997-2015年的全部数据建立预测模型，并对2016-2020年的综合评价指标值进行预测，各个模型预测结果如下：

4.1 趋势外推预测模型

拟合方程：

F=-0.959889719+ 2.738759877 X -0.31266558 X2+0.013818583 X3

预测结果：

表7 用趋势外推模型预测的综合评价指标值(2016-2010年)

4.2 指数平滑预测模型

拟合模型：霍尔特(Holt)双参数线性指数平滑模型, 两参数为=0.9 ,=1

预测结果：

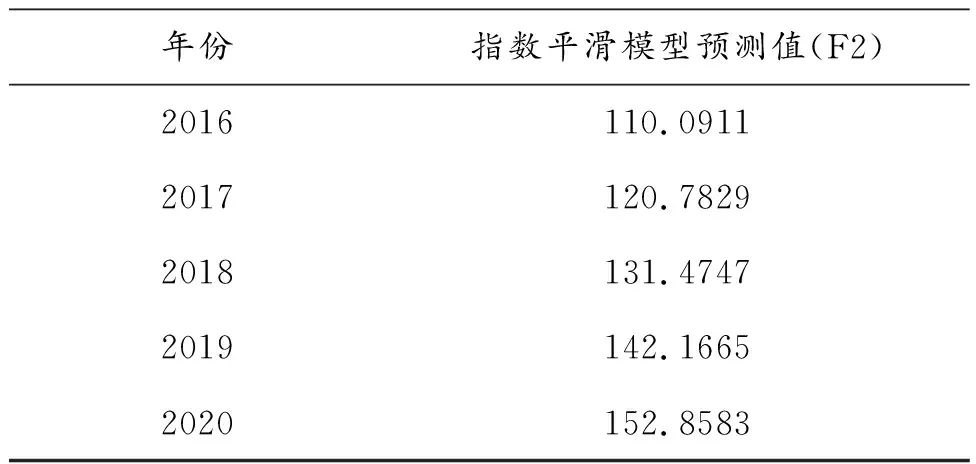
表8 用指数平滑模型预测的综合评价指标值(2016-2020年)

4.3 时间序列预测模型

拟合模型：ARIMA(2，2，2)，模型口径为：

预测结果：

表9 用ARIMA模型预测的综合评价指标值(2016-2020年)

4.4 组合预测模型

拟合方程：

F=0.2595F1+0.4178F2+0.3241F3

预测结果：

由组合预测模型，可以得出2016-2020年我国体育院校发展综合评价指数水平的预测值(见表10)。从预测结果可看出：我国在2020年体育院校生态综合评价指数水平将达到163.19，与2015相比增加了64.11%，我国体育院校生态综合评价指数程度有显著性的提高。

表10 用组合预测模型预测的综合评价指标值(2016-2020年)

5 结论

通过初步建立我国体育院校发展的趋势外推预测模型、指数平滑预测模型、非平稳时间序列预测模型，得出以上单一的预测模型不及组合预测模型效果显著，组合预测模型获得预测值更能减少预测的系统误差，这样就能更好地推断出我国体育院校生态综合评价指数水平的未来走势。