基于时间卷积网络改进的自动数学应用题解算器

杨 波，张 珑，罗琨杰，孙华志

（天津师范大学 计算机与信息工程学院，天津300387）

数学应用题（math word problem）是指一种用自然语言描述的简短问题，问题中包含一些数字和变量信息以及它们之间的数量关系，自动解算器需要理解问题中涉及的逻辑和规则，利用数学知识进行定量推理，计算得到一些未知量，从而得到问题的答案.解决数学应用题涉及自然语言理解和人类问题解决的关键问题，数学应用题常被用作研究自然语言理解的理想对象.

目前，构建自动数学应用题解算器主要有4种方法：①基于模板匹配的方法[1-3]；②基于统计分类的方法[4-7]；③基于树或图的图形方法[8]；④基于深度学习框架的方法[9-11].基于统计机器学习[4-6]和模板匹配[1-2]的方法在小规模数据集上获得了比较满意的结果，但这些方法需要大量的人工操作进行特征提取和模板注释，并且在处理大型或多样化的数据集时，解算器的性能会急剧下降.随着深度学习的兴起，Wang等[9]于2017年首次提出使用seq2seq模型[10]设计解算器，该方法避免了繁杂的特征提取和数据注释工作，同时增强了解算器的泛化性能，对数学应用题解算器的发展做出了里程碑式的贡献.受到文献[9]的启发，文献[12]提出的Ensemble Model模型将解算器建立在seq2seq模型上，通过添加表达式生成规则和规范化策略，提升了解算器的性能.但是，现有工作大多忽略了输入数据的质量这一重要因素，数学应用题复杂多样，解算器对于应用题语义的理解与人的理解存在很大差异，且数学应用题的解决具有较强的时序性，因此，提高输入数据的质量和增强处理应用题的时序性也是提升解算器性能的关键.

算数应用题是以单词序列形式展现的数学问题描述，包含若干已知数量及相应的数学问题.本文针对只需进行简单计算的算数应用题，基于seq2seq模型和时间卷积网络[13]（temporal convolutional network，TCN）提出一种seq2seq+TCN模型构建解算器.该模型选取长短期记忆网络[14]（long short term memory，LSTM）和门限循环单元（gated recurrent unit，GRU）2种循环神经网络[15]（recurrent neural network，RNN）分别作为seq2seq模型的编码器（Encoder）和解码器（Decoder），构成4种不同的seq2seq模型，分别为BiLSTM-LSTM、BiLSTM-GRU、BiGRU-GRU和BiGRU-LSTM，将其应用于构建自动解算器.在数据预处理部分，使用FoolNLTK分词工具[16]和ELMo词嵌入方法[17]，对数据集中的数学应用题进行加工处理，以获得较高质量的输入数据.将TCN加入解码器中，以扩大解码器的感受野，解决一定的时序性问题.在公开数据集Math23K[9]和AI2[8]上进行实验，结果表明，由BiLSTMLSTM构成的seq2seq+TCN模型性能最优，准确率高于现有模型.

1 seq2seq+TCN模型

将数学应用题的解决看作一种映射过程，其中问题文本P作为源序列，其对应的数学表达式模板TP作为目标序列.seq2seq+TCN模型的结构如图1所示，主要包含2个阶段：①数据预处理阶段，将问题文本中出现的数字按照其自然顺序映射到数字标签列表{n1，n2，…，nm}中，经由分词与词嵌入后，获得相应的词向量，用于训练解算器；②训练阶段，每输入一个问题，通过Encoder层获取上下文语义，Decoder层则根据上下文语义从表达式词典中选择相应的数字标签，并重新排列组合，生成正确且可解释的数学表达式，从而得到数学问题与数学表达式的一一映射关系.

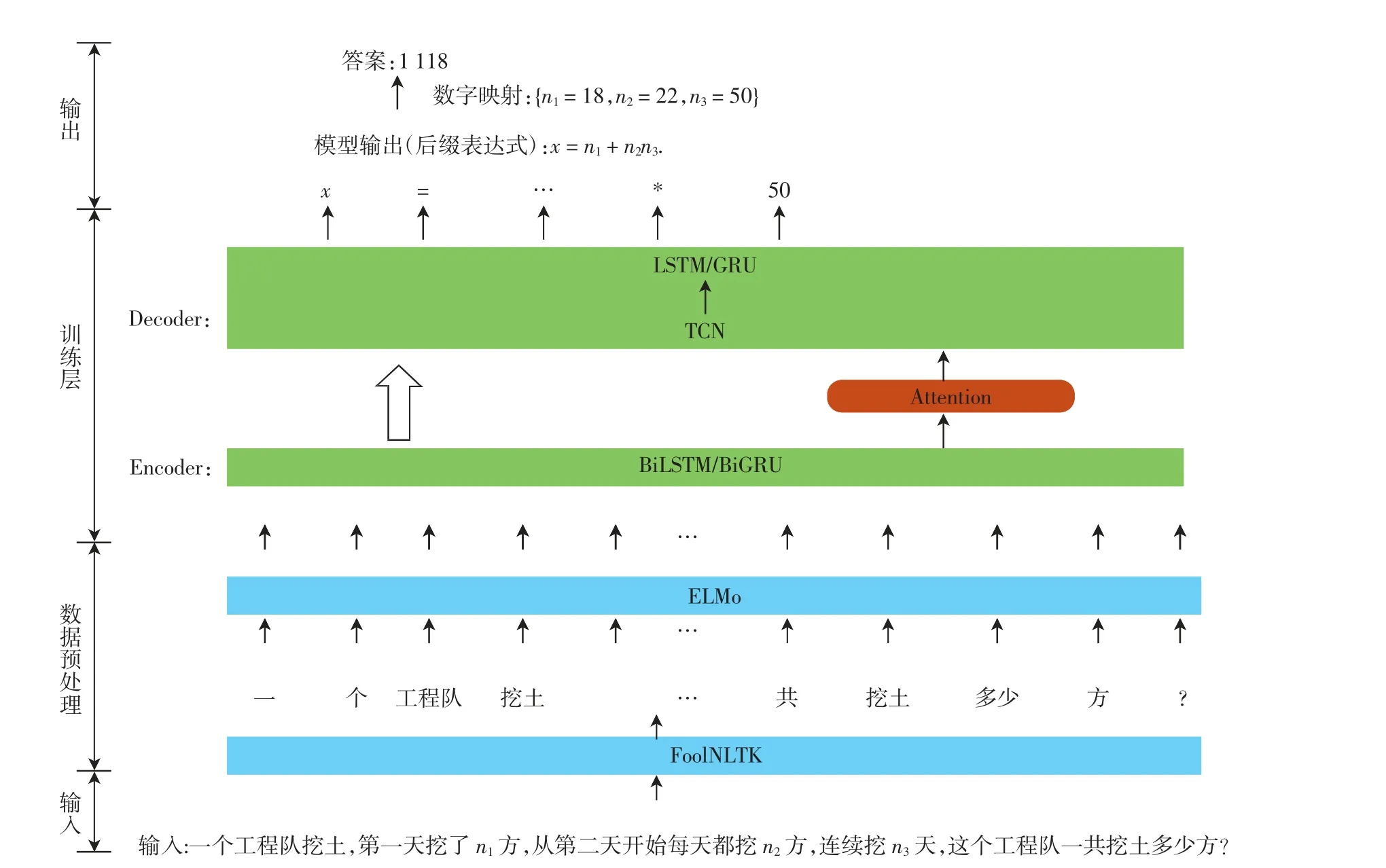
图1 seq2seq+TCN模型Fig.1 Model diagram of seq2seq+TCN

1.1 数据预处理

1.1.1 分词工具

中文分词是将连续的字序列按照一定的规范重新组合成词序列的过程，其目的是辅助机器对自然语言的理解.本文模型处理的数据集既有中文问题，也有英文问题，因此需要选择合适的分词方法.本文使用的FoolNLTK分词工具是一种基于BiLSTM模型训练的分词方法，包括分词、词性标注、实体识别等功能.FoolNLTK对于数学问题这类较为专业性的文本，倾向于将其分为更为离散的词汇，这样有利于组合成更多样的数学问题.对于数学领域涉及的计量单位、运算符号等一些专用词汇，可以将其加入到用户自定义词典中，根据需求设置不同的权重，以使分词结果更加适用于数学运算.

1.1.2 词嵌入方法

由于文本数据的语言类型不同，也需要选择合适的词嵌入方法以获得高质量的词向量.中文文本数据最常用的词嵌入方法是Word2vec，它是一种浅层神经网络，可以较好地表达不同词之间的相似和类比关系，但其训练方式一般是上下文无关的，即同一个词的词向量是固定的，与语境无关，这种方法在处理多义词时会发生错误.本文采用ELMo作为词嵌入方法，该方法以双向语言模型为基础，用各层之间的线性组合来表示词向量.ELMo模型的结构如图2所示，模型的整体结构是BiLSTMs两层激活的串联，不同层的BiLSTM对单词不同类型的信息进行编码，然后连接所有层组合成各种文字表示.ELMo产生的词向量与上下文相关，很大程度上避免了歧义的发生.

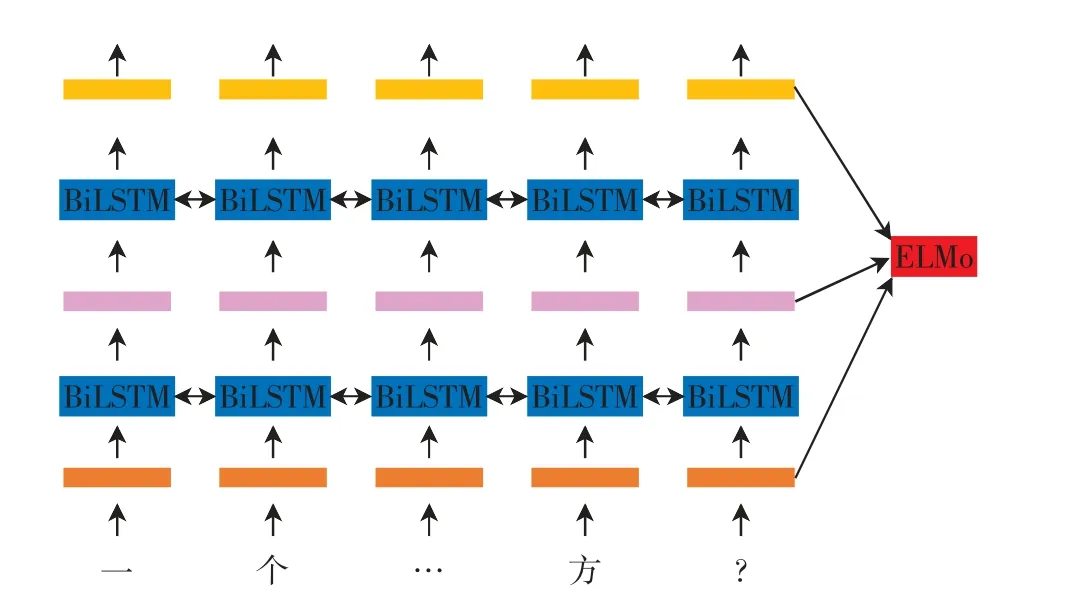
图2 ELMo的结构Fig.2 Structure of ELMo

对于词向量的构建，本文使用已经训练好的128维的ELMo词向量文件来做映射，并将映射后的问题文本P表示为P∈R|P|×128，其中|P|为问题文本的长度.

1.2 训练层

1.2.1 编码器

解算器的编码器需要完成语义捕获，双向RNN不仅能获得当前信息和历史信息，也会捕获到当前位置之后的相关信息，可以全面捕获语义信息.因此，本文将编码器的RNN全部设置为双向RNN，目前最为常用的RNN是LSTM和GRU.

LSTM是一种特殊的RNN，它使用门控机制以更好地建立数据中的长期依赖关系.LSTM的基本操作为：

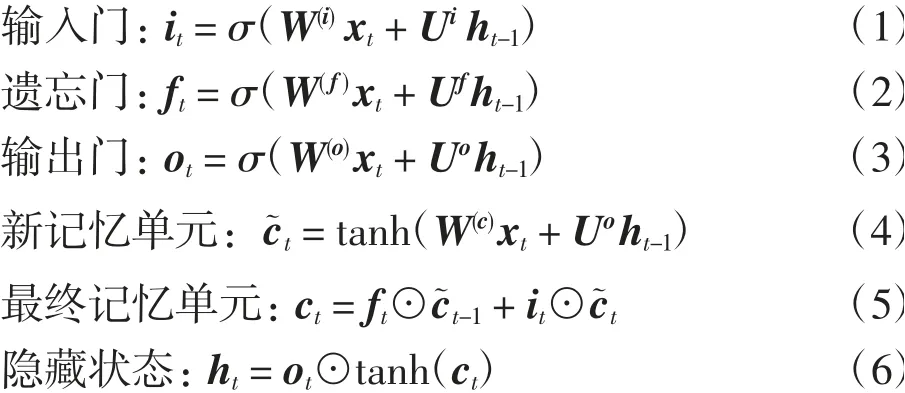
其中：σ为sigmoid函数；⊙表示元素点乘；输入x t由当前单词wt与之前生成的状态r t-1构成.LSTM通过门控机制决定信息的保留或舍弃，解决了RNN的数据长期依赖问题.

GRU是LSTM的简化版本，它保留了LSTM模型的长期记忆能力，主要变动是将LSTM中细胞的输入门、遗忘门、输出门替换为更新门和重置门，并将细胞状态和输出2个向量合二为一.GRU的的基本操作为：

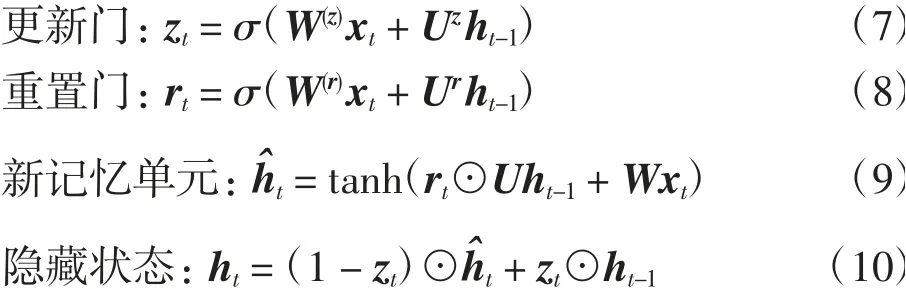
编码器将经过数据预处理后的问题文本P输入到两层双向RNN，并将两层双向RNN的输出拼接起来，获得编码器输出EP[max_length，batch_size，seq_len]，以及最后一个时间步的隐藏层状态HP[n_layers×2，batch_size，hidden_size]，这个隐藏状态包含了整个序列的信息编码，即语义编码，其中：max_length为文本序列最大长度；batch_size为批处理大小；seq_len为问题文本长度；hidden_size为隐藏单元数；n_layers为RNN层数，本文使用双向RNN，因此对n_layers做乘2操作.

1.2.2 注意力层

为提高模型运行效率，在编码器与解码器之间加入注意力（Attention）机制.通过计算源序列和目标序列的加权和，从大量信息中有选择地筛选出重要信息.Attention机制的具体操作为：

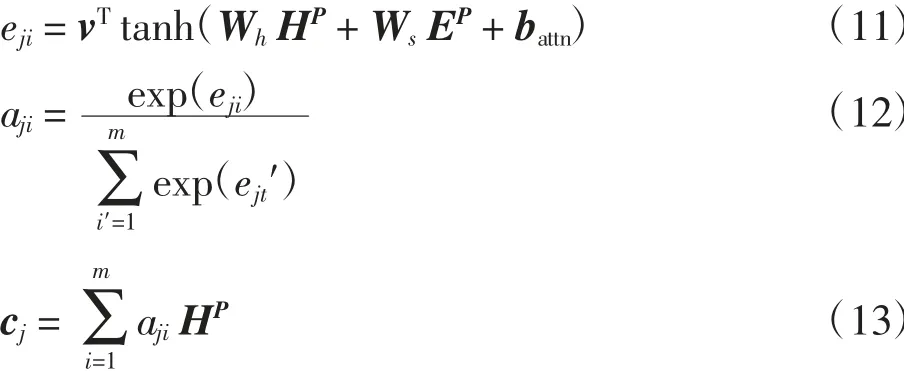
其中：aji定义了注意力在输入词上的概率分布，由未标准化的注意力得分eji计算得到；c j为上下文向量，是编码器隐藏状态的加权和.

1.2.3 解码器

解码器根据编码器传递的上下文向量预测并生成数学表达式.在解算器生成的数学表达式中，数字标签应尽量按照其在源文本中的顺序排列，以减少生成表达式的数量，这要求表达式中元素的出现具有一定的时序性.解决时序性问题有2个关键要求：①输出时序数据（y）和输入时序数据（x）大小要一致；②时刻t的预测输出y t只能由时刻t之前的输入x1，…，x t-1确定.TCN网络中的空洞卷积可以使每个隐层的序列都与输入序列的大小一样，同时降低计算量，扩大感受野，另外，TCN网络的残差卷积可以将下层特征拿到高层增强生成当前信息y t的准确率.因此，本文在解码器中加入TCN网络，其结构如图3所示.TCN网络由因果卷积和空洞卷积组成.对于输入序列x∈Rn和滤波器f（i），空洞卷积对序列中的元素s进行如下操作：

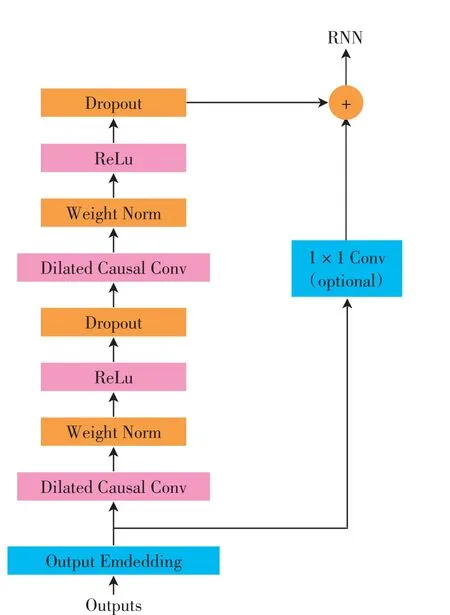
图3 TCN的结构Fig.3 Structure of TCN

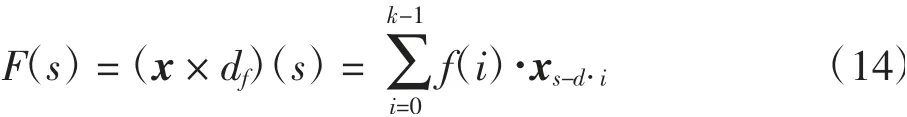
其中：d为膨胀系数；k为过滤器尺寸（取k=3）；s-d·i代表过去的方向.当d=1时，扩张卷积减小为规则卷积.使用较大的扩展可以使顶层的输出表示更广泛的输入范围，从而有效地扩展上下文向量的接收字段.

本文模型将TCN和RNN结合使用，在预测表达式序列y1，y2，…，y t时，对每个时间步t，解码器基于y1，y2，…，y t-1和语义编码HP得到y t的条件概率；解码器的前馈网络中的RNN使用前一步的输出与隐藏状态HD′作为当前时间步的输入ID[batch_size，1，hidden_size]，计算当前时间步的输出以及隐藏状态HD.本文模型将每个时间步的输入ID首先经过一层TCN网络，虽然其维度构成没有发生变化，但其扩大了对输入内容的感受野，并补充了注意力机制中所缺失的时序性，将处理后的数据再经过RNN网络来预测每一时间步的输出.

在数字映射阶段，表达式模板TP已经获得.表达式可能出现冗余项或者括号匹配等问题，本文采用文献[12]的规范化策略进行处理：①将2个长度不等的重复表达式模板规范化为较短的模板；②表达式模板中出现数字标签的顺序要尽量与问题文本P一致；③利用表达式树的唯一性[9]解决括号匹配问题.

2 实验结果与分析

2.1 数据集

本文使用Math23K和AI2数据集进行实验.

Math23K包含23 161个中文数学应用题，它们是从在线教育网站上超过60 000个应用题中利用一种基于规则的提取方法得到的.该数据集中的所有问题都具有完整标签，且仅涉及线性单变量数学问题与加、减、乘、除4种基本运算，题目类型丰富，规模大，是验证深度学习方法的首选.

AI2数据集来源于math-aids.com和ixl.com 2个网站，包含395个三、四、五年级的单步或多步英文数学应用题，问题类型只涉及加法和减法，每个数学问题都包含多个数量，并有可能包含与解决方案无关的量.

2.2 实验设计与参数配置

首先，采用FoolNLTK+ELMo技术进行数据预处理.然后，选择GRU和LSTM组合成4种不同的seq2seq模型建立数学应用题解算器.最后，在seq2seq中添加TCN网络，依次记为seq2seq+TCN（BiLSTM-LSTM）、seq2seq+TCN（BiLSTM-GRU）、seq2seq+TCN（BiGRUGRU）和seq2seq+TCN（BiGRU-LSTM）.

对于Math23K，分别随机抽取1 000个问题作为验证集和测试集，其余作为训练集.AI2规模较小，将其以6∶2∶2的比例划分为训练集、验证集和测试集，验证集用于调试超参数.模型的参数配置见表1.

表1 参数配置Tab.1 Parameter configuration

2.3 实验结果与分析

为了对模型效果进行评估，将本文模型与2个具有代表性的集成seq2seq的自动数学应用题解算器[9，12]进行比较.文献[9]的DNS+Retrieval算法，通过设置一个超参数θ作为相似度阈值，将检索模型和seq2seq模型结合，当测试问题PT与检索问题Q的Jaccard相似度大于θ时，利用Retrieval算法直接选择Q的表达式模板作为PT的表达式模板，否则利用seq2seq模型自动生成表达式模板，省去了繁琐的人工特征提取.文献[12]提出的Ensemble Model算法选择RNN、ConS2S和Transformer 3种常用于机器翻译的seq2seq模型，根据概率公式计算选择最优的seq2seq模型生成表达式，并添加了一些对于表达式的规范化策略.以答案准确率衡量模型的性能，以上2种方法和本文模型在数据集Math23K和AI2上的答案准确率见表2.由表2可见，在大型中文数据集Math23K和小型英文数据集AI2上，基于BiLSTM-LSTM的seq2seq+TCN模型的答案准确率均为最高，分别达到70.3%和87.5%.

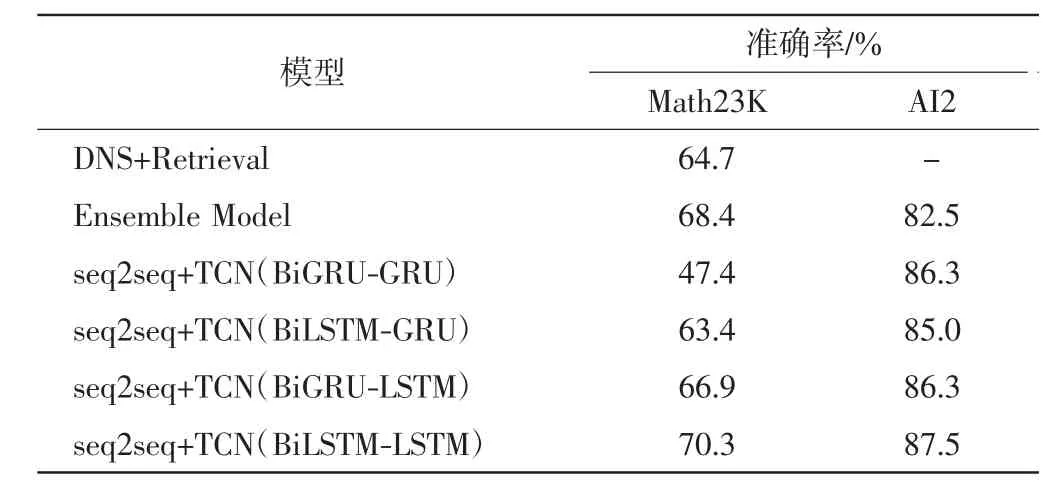
表2 不同模型在Math23K和AI2数据集上的准确率Tab.2 Accuracies of different models on Math23K and AI2 datasets

为验证数据预处理的重要性，对Math23K验证集的数据进行手工分词，并比较了Jieba与FoolNLTK 2种分词工具的准确率、召回率和F1 3个性能指标，结果见表3.由表3可见，FoolNLTK的分词质量明显优于Jieba，F1从66%提升至90%.

表3 2种分词工具的性能比较Tab.3 Performance comparison of two word segmentation tools

为评价数据预处理方法在解算器中的作用，分别在2个数据集上比较了Jieba+Word2vec和FoolNLTK+ELMo方法对seq2seq+TCN模型性能的影响，结果见表4.由表4可见，在Math23K和AI2上，FoolNLTK+ELMo方法的性能均优于Jieba+Word2vec.在小型数据集AI2上，由于英文具有天然的分隔符，分词工具的作用不大，所以模型性能的提升主要源于词向量嵌入方法ELMo，ELMo得到的词向量的质量明显优于Word2vec方法.本文采用的FoolNLTK分词工具和ELMo词嵌入方法均对模型性能的提升有所帮助.

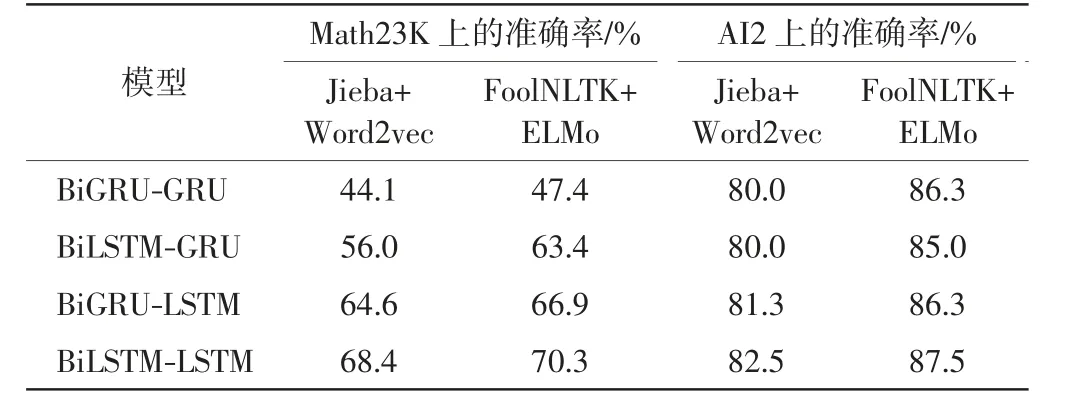
表4 不同数据预处理方法对模型性能的影响Tab.4 Impacts of different data preprocessing methods on the performances of models

另外，本文分别在2个数据集上比较了加入和不加入TCN网络对seq2seq+TCN模型性能的影响，结果见表5.由表5可见，在Math23K和AI2上，TCN网络的加入使模型准确率分别提升约1.225%和1.875%.在解码器中加入TCN网络，解决了注意力机制中欠缺时序性的问题，并扩大了解码器的感受野，起到一定的特征增强的作用.

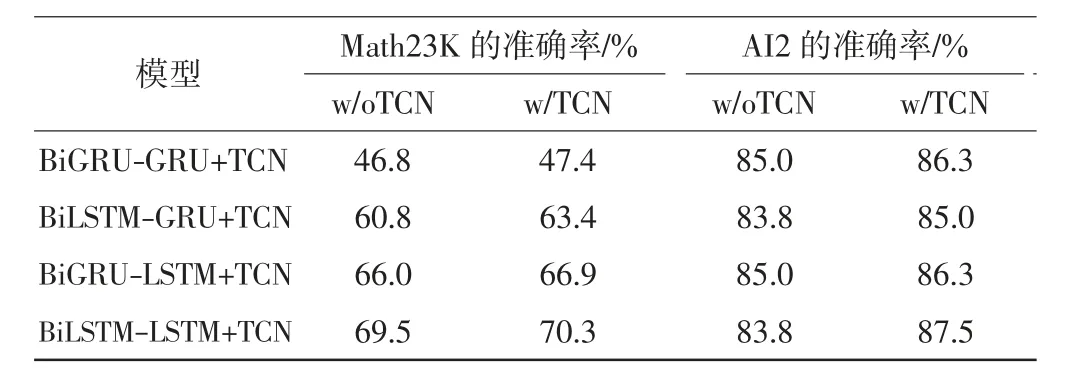
表5 TCN网络对模型性能的影响Tab.5 Impacts of TCN on the performances of models

3 结语

本文提出seq2seq+TCN模型设计自动数学应用题解算器，采用FoolNLTK分词工具和ELMo词嵌入方法优化数据预处理操作，以获得高质量的输入数据，将TCN与RNN结合使用，扩大了解码器的感受野，解决了一定的时序性问题.在大型中文数据集Math23K和小型英文数据集AI2上进行实验，对比了选用不同RNN组合的seq2seq+TCN模型的性能，结果表明，基于BiLSTM-LSTM的seq2seq+TCN模型性能最优，其答案准确率高于现有的2个具有代表性的集成seq2seq的解算器.在未来的研究中，希望在模型中加入更适合于数学文本解析的相关特征以辅助解算器理解数学问题，从而进一步提高解算器性能.