Onboard actuator model-based Incremental Nonlinear Dynamic Inversion for quadrotor attitude control:Method and application

Zexin WANG,Jiang ZHAO,Zhihao CAI,Yingxun WANG,Ningjun LIU

School of Automation Science and Electrical Engineering,Beihang University,Beijing 100191,China

KEYWORDS Actuator;Attitude control;INDI;NDI;Quadrotor

Abstract This paper addresses the robust attitude control problem for quadrotors subject to model mismatch and disturbances.A dynamic inversion based attitude control scheme is proposed,which consists of an outer loop attitude controller and an inner loop angular acceleration controller.The attitude controller is designed based on the Nonlinear Dynamic Inversion(NDI)to precisely linearize the nonlinear dynamics between the angular acceleration and the attitude.An onboard actuator model-based Incremental Nonlinear Dynamic Inversion (INDI) controller is designed in the angular acceleration control loop to improve the robustness against the model mismatch and disturbances.Meanwhile,the onboard actuator model with a modified structure eliminates the oscillation phenomenon when the sampling rate of the controller is higher than that of the actuator.Numerical simulations and flight tests demonstrate the effectiveness and robustness of the proposed controller in comparison with the PID controller.

1.Introduction

In recent years,the unmanned rotorcraft vehicle received increasing attention in research.1–3It can carry multiple types of equipment to perform military or civil tasks,such as surveillance,navigation,rescue,media,and delivery.4,5.But in order to accomplish these tasks in complex environments,the quadrotor vehicles need high disturbance rejection capabilities,which increases the difficulty of attitude controller design.

Many linear control algorithms have been applied to the flight control design for quadrotors,such as PID control,6,7Linear Quadratic Regulator/Gaussian (LQR/LQG),8and robustH∞control.9However,they are both designed based on the linearized dynamics model.When the vehicle performs high speed or big attitude angle maneuvers,its nonlinear effects are not negligible.

Thus,many attempts have been made to use nonlinear control techniques in the flight controller design of the quadrotor vehicles,such as dynamic inversion,10backstepping,11,12sliding mode,12,13and adaptive control.14,15Some control schemes even combine multiple control algorithms,16,17and adapt different disturbance observers to the controller,18,19to improve the robustness of the controller.Although the disturbance rejection capability is improved,the complexity of the controller is also greatly increased.While these complex methods may be desired from a control theory standpoint,it is challenging to adapt these methods to different quadrotors for lack of transparency between the control parameters and the resulted response.20

One of the straight forward and practical nonlinear control techniques is the Nonlinear Dynamic Inversion (NDI).Theoretically,it transforms the original nonlinear dynamics into the desired linear one.In recent years,the NDI control approach has achieved some success in practical applications.21,22But it is sensitive to model mismatch.In this paper,NDI is used as a part of the whole attitude controller to linearize the nonlinear dynamics between the attitude and angular accelerations of the quadrotors.Because these dynamics can be precisely modeled based on the kinematic equations with no model-related parameters such as the aerodynamic coefficients and the control effectiveness.

The Incremental Nonlinear Dynamic Inversion(INDI)is a robust Nonlinear Dynamic Inversion method which retains the advantages of the NDI technique and increases the robustness.It is a sensor-based robust control approach which uses the estimations of the acceleration from sensor data to replace the plant dynamics model used in NDI.Therefore,in the case of controlling highly nonlinear plant,it can achieve strong robustness to model mismatch and faster response to disturbances.23,24In this paper,it is used in the angular acceleration control of the quadrotor.

Although there are some successful applications of INDI to the quadrotor platforms,23,25previous studies ignored the oscillation phenomenon of the INDI controller when the controller sampling rate is higher than that of the actuators.Few studies have paid attention to the applicability of the INDI controller with onboard actuator models when applied to the quadrotors with low sampling rate actuators.It has been proven theoretically that the INDI controller with a higher sampling rate has a larger stability margin and better performance.26But in practice,the maximum sampling rate of the actuator is limited by the hardware.For instance,the maximum Pulse Width Modulation (PWM) frequency for most servos ranges from 40 Hz to 200 Hz,27and the maximum sampling rate of the Electronic Speed Controllers (ESC) with conventional PWM protocols is lower than 500 Hz.28This phenomenon is easily overlooked when using highperformance actuator hardware or a lower controller sampling rate.However,it should be considered in the INDI controller structure to avoid the limitation of actuator hardware.If we ignore the difference in sampling rate,the estimated current actuator position will not be synchronized with the actual value.This causes oscillation.

The main contributions of this paper are:(A) An easy-totune robust attitude controller for quadrotor platforms is designed,which consists of an NDI control loop and an INDI control loop to counteract the nonlinearity,model mismatch,and the disturbances.(B) A modification is made inside the INDI controller to compensate for the sampling rate mismatch between the controller and the actuator.It extends the applicability of the INDI method on quadrotor platforms with low sampling rate actuators.(C) Both flight tests and simulations are conducted to demonstrate the performance and robustness of the proposed controller.(D)The disturbance rejection capability of the proposed controller is compared to that of a welltuned PID controller in both simulations and flight tests.

This paper is organized as follows.A 6 degree-of-freedom quadrotor dynamics model and the basic theory of INDI are presented in Section 2.The proposed controller is designed in Section 3.Numerical simulation results are presented in Section 4.Flight test results are presented in Section 5.Conclusionsare drawn in Section 6.

2.Preliminaries

2.1.Quadrotor model

A 6 degree-of-freedom quadrotor is shown in Fig.1(a).The body-fixed coordinate system is used in modeling forces and moments of the quadrotor,andlx,lyare the moment arm of the rotors.

The vehicle rotational dynamics are given by

whereyis the output vector,η=[φ,θ,ψ]Tis the Euler angle vector,Ω=[p,q,r]Tis the angular velocity of the quadrotor,Jis the vehicle moment of inertia tensor.The moment vector generated by the rotors is denoted asM,and the external disturbance moment is denoted asMext.And Tηis the transformation matrix between attitude rate and body angular velocity:

To improve the fidelity of the model,the force and torque of the rotor are measured in the bench test with zero inflow airspeed as shown in Fig.1(b).The force and torque of each rotor are denoted as TiandQi,(i=1,2,3,4),which can be presented as quadratic functions of the rotor’s rotation speed:

Fig.1 Hardware configurations.

where ωiis the rotation speed of each rotor,kτthe rotor thrust coefficient,kqthe rotor torque coefficient.The bench test data is fitted using quadratic functions in Eq.(3),as shown in Fig.2.The fitting results are kτ=9.25×10-6and kq=1.136×10-7.The effect of the inflow airspeed is ignored and treated as the model uncertainty in the controller design.

Fig.2 Results of the rotor bench test.

Then the moments generated by the rotors is calculated using Eq.(3)to obtain the control coefficientsG1andG2which are used in the controller design:

Where the Hadamard power,ω=[ω1,ω2,ω3,ω4]Tthe rotation speed vector of the rotors,lx,lythe length of the moment arms which are shown in Fig.1,andIrthe propeller moment of inertia.Additional gyroscopic moments of the rotors aboutbxandbyaxis are negligible.29Only thez-component of the rotor gyroscopic moment is considered.

2.2.Incremental Nonlinear Dynamic Inversion (INDI)

The general form of a nonlinear,non-affine system is

wherex(T) is the state vector,u(T) is the control input vector,y(T) is the output vector.Instead of inverting entire system dynamics like the NDI,INDI linearizes and inverses the system dynamics at the current statex0and control inputu0.

Rewriting Eq.(7)by using a first-order Taylor series expansion and neglecting high order terms yields

Due to the short sampling time of the flight control computer and relatively fast response speed of the actuator,the contribution of Δxon the output derivative is negligible as compared to Δu.23Hence,Eq.(8) can be simplified as

3.Robust attitude control with sampling rate compensation

The overall attitude controller comprises an outer control loop and an inner control loop.The outer loop calculates the desired pseudo controls using pilot commands and attitude and angular rate feedback signals based on the NDI control law.The inner loop produces the rotor control signals incrementally based on the INDI control law.The structure of the proposed attitude controller is shown in Fig.3.It is a sampled-data system and the real actuator and quadrotor dynamics are discretized in the closed-loop analysis.

Fig.3 Overall controller structures.

3.1.NDI based outer loop controller

The second-order differentiation of the Euler angles expressed by the angular velocity vector Ω and the transformation matrix Tηis derived from Eq.(1):

The outer loop NDI controller is designed to track the pilot’s attitude command with the desired dynamic response.The body angular accelerationis the input of the system shown in Eq.(11).So the NDI controller can accurately cancel out the original dynamics in Eq.(11) without any model related uncertain parameters,which avoids the effects of model mismatch.

The dynamic response is determined by the virtual controlIt takes the form of a PD controller to guarantee the secondorder dynamics of the desired closed-loop attitude response:

wherekηandk˙ηare the gains tuned according to the frequency and damping ratio requirement of the system,ηcis the pilot’s attitude command.Finally,the pseudo controlwhich is the input of the inner loop controller is derived by bringing Eq.(12) to Eq.(11):

3.2.INDI based inner loop controller with sampling rate compensation

A simplified first-order Taylor series expansion of Eq.(1) is

withω0the vector of current rotor rotation speed andthe current angular acceleration vector.The partial derivative of the moment in Eq.(14)is calculated from Eqs.(4)-(6).In order to get the derivative,Eq.(4) is discretized using finitedifference approximation over the controller sampling time ΔT,which yields

withωcthe command of rotor rotation speed.Note that in Eq.(17),the predicted angular accelerationis replaced by the desired angular accelerationfrom the NDI controller.

The filter cut-off frequency ωnis tuned according to the vibration characteristics and the bandwidth of the vehicle.In the meantime,the estimated angular acceleration is delayed because of the filter.All the terms in Eq.(17) should be synchronous,otherwise,the equation will become incorrect and the closed-loop system will oscillate.29For this reason,the current rotor angular velocityω0is filtered by the same low-pass filter.The filtered term in Eq.(17) is rewritten with the subscriptf.

In order to obtain the current rotor rotation speedω0,we use a modified actuator model to estimateω0for lack of extra rotation speed sensors and the rotation speed feedback from the electronic speed controllers of the rotors,as shown in Fig.4.The dynamics between the motor’s rotation speed setpoint and its response can be represented as a continuous first-order transfer function.

where ωci,is the rotation speed command of each rotor,τathe time constant of the actuator that can be obtained by parameter identification.

The main difference between the original INDI controller and the proposed INDI controller is that a ZOH is separated in the onboard actuator model whose sampling rate can be designed based on the actuator’s sampling rate to compensate the sampling rate mismatch between the controller and actuator.In original applications,the onboard actuator model is discretized with the sampling rate of the controller,in which the sampling-rate-tunable ZOH is ignored,23,29,as shown in Fig.4.

The modified actuator model in the INDI controller feedback loop is discretized,during which a ZOH is added and its sampling rate is designed separately as shown in Fig.4(b).The resulted discrete actuator model is

Fig.4 INDI controller structure.

with Tmthe sampling time of the ZOH.

Special care should be taken when setting the sampling rate of the ZOH in the actuator model.In conventional applications,the actuator model is discretized with the sampling rate of the controller,in which the sampling-rate-tunable ZOH is ignored.But in this paper,Tmis designed independently to compensate for the difference between the high controller sampling rate and the low actuator sampling rate.The derivation of Tmis illustrated in the next section.

3.3.Closed-loop analysis based ZOH sampling rate design

The function of the independent ZOH can be illustrated based on the linear analysis of the attitude control closed-loop system.The angular acceleration closed-loop system of the INDI controller along with the discretized quadrotor rotation dynamics is shown in the block diagram of Fig.5.

Fig.5 Angular acceleration closed-loop system.

WhereA(z) is the discretized motor dynamics with a sampling time Ta;is the aforementioned modified actuator model with a sampling time Tm;Tsis the sampling time of the controller;Gis the simplified representation of the control effectiveness matrix.Then the closed-loop angular acceleration transfer function can be derived:

It is shown from Eq.(22) that the closed-loop angular acceleration dynamics are not only determined by the motor dynamics but also by the sampling times of the real actuator and the onboard actuator model.

To evaluate the effect of the sampling rate mismatch on the closed-loop response,a simplified linear quadrotor dynamics model is used.In standard hover flight,the body angular rates and pitch roll angles are zero.So the closed-loop system containing the NDI and INDI controller and the quadrotor dynamics can be linearized,as shown in Fig.6.

Fig.6 Attitude closed-loop system.

Note that the control system is discretized for frequencydomain analysis using z-transform because the control system is a sampled-data system which contains a continuous plant and a discrete controller running on the flight control computer.By closing the attitude and angular rate control loop,the final closed-loop transfer function of the attitude dynamics is derived.

In the ideal case where Tm=Ta,the angular acceleration transfer function becomes

Then the attitude response is nearly a typical secondorder response ignoring the fast dynamics of the actuator.But if Tm≠Ta,the attitude response degrades because of the oscillation caused by the dynamics not canceled out in Eq.(22).

The oscillation phenomenon caused by the sampling rate mismatch can be illustrated using the dominant poles of the closed-loop linear transfer function.Two typical cases with different Tmare studied.Their parameters are listed in Table 1.

The dominant poles of each case are calculated using the closed-loop transfer function and compared in Fig.7.The frequency and damping ratio of each of the poles are listed in Table 2.

Fig.7 Dominant poles for different pairs of Tm and Ta in the zplane.

Table 1 Control parameters in the linear analysis.

As a consequence of the dynamics not canceled out in Eq.(22),a pair of high-frequency underdamped poles with an overshoot of 43.2% arise in Case 1.Thus its time-domain response oscillates which is shown in the simulation results in the next section.And in Case 2,the high-frequency underdamped poles disappear with the help of the tuned sampling rate in the modified actuator model.So the difference between the controller sampling rate and the actuator sampling rate can be successfully compensated by the modified onboard actuator model with Tmset to the same value as Ta.

It can be seen from the above controller design process that there are four tunable parameters for each control channel:kη,k˙η,ωn,and Tm.Among them,Tmis determined by the actuator sampling rate and does not need tuning;the filer cut-off frequency ωnis determined by the vibration characteristics and the bandwidth of the overall closed-loop system.Once these hardware-related parameters are settled down,the handling quality of the vehicle is only determined by kηand k˙η,which makes the parameter tuning easy and transparent.

4.Simulation tests

4.1.Effectiveness of the modification in INDI

In order to verify the effectiveness of the modified onboard actuator model when applied to quadrotors with low sampling rate actuators,several cases are studied in the simulation with the nonlinear quadrotor model.The key parameters of the quadrotor platform are listed in Table 3 and the control parameters of the cases are listed in Table 4.

Table 2 Frequency and damping ratio of the dominant poles.

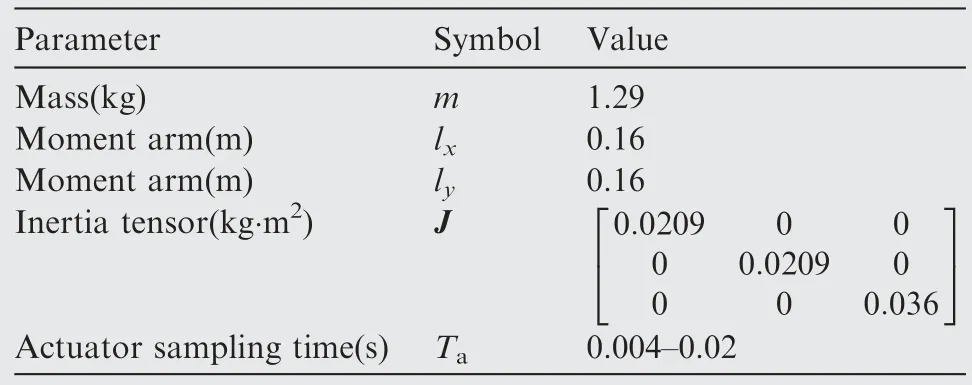
Table 3 Parameters of the quadrotor platform.

Table 4 Control parameters in simulation tests.

The simulation results of the three cases are shown in Fig.8.

Fig.8 Attitude responses for Case 1–3.

In Case 1,the parameters are set to the nominal values,and the attitude response has a rise time less than 0.4 s and a small overshoot.It is concluded from the results that with the help of the modified onboard actuator model in the INDI controller,the oscillation phenomenon is avoided and the performance of the controller does not degrade much when using low sampling rate actuators.

4.2.Robustness against disturbances

The disturbance rejection capability of the proposed controller is examined and compared to that of a well-tuned conventional PID attitude controller through simulations.The simulation tests are conducted with the following procedures.

(1) The sampling rate of the actuator is set to 50 Hz,and the sampling rate of the controller is 250 Hz.

(2) The gains in the PID controller are tuned manually to make its response as fast as the proposed controller.Their step responses are compared in Fig.9(a).

(3) In the hovering state,constant external roll and pitch disturbance moments are applied to the quadrotor model at the same time.The magnitude of the disturbance moment is 0.32 N∙m,which is 25% of the maximum control torque of the studied quadrotor.

(4) The same test is repeated using the PID controller and the proposed controller respectively.And the disturbance rejection responses for the two controllers are compared in Fig.9(b).

Fig.9 Step response and disturbance rejection response for the PID controller and INDI controller.

The peak value of the disturbance rejection response for the proposed controller is 2.9°which is only 43.6%of PID is.And the settling time of the response for the proposed controller is 1.34 s which is 39.3% of PID.Because the INDI controller directly estimates and compensates the disturbance in accelerations,but the PID controller uses the integration of the errors in attitude angles or angular rates to compensate for the disturbance.And its integrator gain is limited by the stability requirement of the controller,which means a trade-off must be made between the stability and disturbance rejection capability during the design of the PID controller.

4.3.Robustness against model mismatch

The important model-related parameter used in the INDI controller is the control effectiveness of rotors.And it is hard to bemeasured accurately especially in high-speed flight or with different inflow angles of rotors.In the design process,only the nominal value of the control effectiveness is used.Here,its robustness against control effectiveness perturbations is checked.The control effectiveness of the rotor is denoted as:

The nominal value ofKis denoted aswhich is used and kept unchanged in the INDI controller.Perturbations are added onKin the simulation model:

For comparison,the same simulation is also done with the PID controller.The attitude responses for the PID controller and the proposed controller with different values of Δ are shown in Fig.10.

Fig.10 Response with model mismatch.

It is shown that the proposed controller is less sensitive to the control effectiveness perturbation than the PID controller.Although the model mismatch affects the responses for both the PID controller and the proposed controller,its influence is smaller on the proposed controller.And the change in the overshoot or damping ratio of the PID controller is severer than the proposed controller.

5.Flight tests

5.1.Effectiveness of the modification in INDI

To validate the performance of the proposed attitude controller,several flight tests have been conducted using a general quadrotor platform.The flight test is shown in Fig.11.The flight controller runs PX4 open-source software with a sampling rate of 250 Hz.Linear acceleration and angular rate are measured by the onboard IMU.High-performance ESCs and motors are used which allows PWM frequency range up to 500 Hz to enable different PWM frequency settings in different flight tests.The sampling rate of the actuator is changed by the PWM output frequency setting of the controller.Table 5 lists their parameter settings.

Fig.11 Animation of flight tests.

Table 5 Flight test settings.

Flight test 1 represents the ideal case where the sampling rate of the quadrotor’s actuator is as high as the controller’s sampling rate.In this flight test,the performance of the nominal controller is evaluated.Flight tests 2 and 3 simulate the situation when applying the INDI controller to the quadrotors with low sampling rate actuators.And,in flight test 3,the ZOH sampling rate is tuned to 50 Hz to compensate for the difference between the sampling rates of the controller and actuator.The attitude responses are shown in Fig.12.

It is concluded from these results that the modification in the INDI controller successfully eliminates the oscillation phenomenon without degrading the command tracking performance.The flight test results agree with the closed-loop analysis and the simulation results.In test 1 and test 3,the roll and pitch angle reaches the reference value within 0.5 s and the responses are well-damped.And as mentioned in previous sections,if the difference between the controller sampling rate and the actuator sampling rate is ignored,the estimated current actuator position cannot synchronize with the actual value.The unsynchronized signal will cause controller oscillation,which can be seen explicitly in Fig.12(b).This problem is solved by adding a separated ZOH in the onboard actuator model in the INDI controller and setting its sampling rate to the same value as the actuator sampling rate.Its effect can be seen clearly in Fig.12 (c),where the oscillation disappears and the command tracking response has little difference from that in flight test 1.

Fig.12 Attitude responses for flight test 1–3.

5.2.Comparison of the disturbance rejection capability

The disturbance rejection capability of the proposed dynamic inversion based attitude controller is compared with that of a well-tuned PID controller used in the simulation test.The flight tests are conducted with the following procedures.

(1) The sampling rate of the two controllers is set to 250 Hz.And the PWM frequency and the ZOH sampling rate is set to 50 Hz.

(2) A constant additional roll moment is applied to the quadrotors in the hovering flight to simulate the external disturbance.The roll moment is generated by adding an extra asymmetric thrust command to the rotors mounted on the left and right side of the quadrotors at the same time.And the direction of the resulted artificial disturbance moment is along the positive direction of the bx-axis and its magnitude is about 0.12 N∙m to ensure flight safety.

(3) The same artificial disturbance moment is applied to the same quadrotor platform controlled by the proposed controller and PID controller respectively.The flight results are shown in Fig.13.And the data is extracted and compared with synchronized timestamps in Fig.14.

Fig.13 Disturbance rejection responses.

Fig.14 Comparison of the disturbance rejection response for the proposed controller and PID controller.

The flight test results validate that the proposed controller has a higher disturbance rejection capability than the PID controller.The peak value of the response for the proposed controller is 1.56°which is much smaller than the PID controller’s 4.5°.And the settling time of the response for the proposed controller is 0.75 s which is much shorter than the PID’s 2.22 s.

6.Conclusions

(1) This paper presents an easy-to-tune INDI based robust attitude controller which can be applied to the quadrotor platforms with low sampling rate actuators.The controller consists of an NDI attitude and angular rate control loop and an INDI angular acceleration control loop to counteract the nonlinearity,model mismatch,and the disturbances.A modified onboard discrete actuator model is proposed to compensate for the difference between the controller sampling rate and actuator sampling rate.

(2) Both simulation and flight test results demonstrate the effectiveness of the modified actuator model and the robustness of the entire controller.And the disturbance rejection capability of the proposed controller is also compared to that of a well-tuned PID controller in the simulation and flight tests.The results show that the proposed controller has a higher disturbance rejection capability and higher robustness against model mismatch than the conventional PID controller.

(3) The controller designed in this paper can bring two benefits.First,the high disturbance rejection capability allows the quadrotors to operate in complex environments with satisfactory performance.Second,the modified onboard actuator model in the INDI controller extends the applicability of the INDI method on different quadrotor platforms with low sampling rate actuators.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This study was co-supported by the National Natural Science Foundation of China(Nos.61803009,61903084)and the Fundamental Research Funds for the Central Universities of China (No.YWF-20-BJ-J-542).