Supersonic flutter control and optimization of metamaterial plate

Wei TIAN,Tian ZHAO,Yingsong GU,Zhichun YANG

School of Aeronautics,Northwestern Polytechnical University,Xi’an 710072,China

KEYWORDS Local resonators;Metamaterial plate;Nonlinear aeroelastic responses;Parametric optimization design;Supersonic flutter control

Abstract A metamaterial plate is designed by embedding a periodic array of local nonlinear resonators for its supersonic flutter control.Based on the von Karman large deformation theory and supersonic piston aerodynamic theory,the nonlinear aeroelastic equations of the metamaterial plate are obtained by using the Hamilton principle.The comparisons for aeroelastic behaviors of the metamaterial plate and pure plate show that the proposed metamaterial plate can lead to an enlarged flutter boundary and lower vibration amplitude.Furthermore,a parametric optimization strategy for local nonlinear resonators is proposed to improve the nonlinear flutter behaviors of the metamaterial plate,and a significant enhancement of passive control performance can be achieved through optimization design.The present study demonstrates that the design of the metamaterial plate can provide an effective approach and potential application for nonlinear flutter suppression of supersonic plate.

1.Introduction

Panel flutter is a self-excited oscillation of the skins structure of flight vehicles which are exposed to supersonic or hypersonic airflow on one side.1,2As the design of flight vehicles trends toward high speed,high maneuverability and lightweight,the thin-walled structures with high strength and new type of materials have been widely applied to the structural design of flight vehicles.As a result,these thin-walled structures may behave nonlinear flutter phenomena because of geometric nonlinearity by large deformation,which could cause fatigue failure of structures.3,4Thus,the demand of nonlinear flutter suppression technology for panels becomes necessary and important.

Recently,the concept of metamaterials,where subunits or local resonators are designed and embedded in the primary structure with conventional materials,has been extended to vibration and acoustic suppression.5–7These metamaterial structures show some unique dynamic behaviors,such as bandgap,low frequency absorption and directional propagation.8–9The designs of various metamaterial structures have been introduced into the vibration control of panels and shells.Basta et al.10studied the vibration mitigation of the nonlinear metamaterial beam by attaching a distributed array of local absorbers and performed an optimization design for obtaining desired resonant frequency.Subsequently,they proposed a rotating metamaterial cantilever beam with embedded springmass-damper subunits for vibration reduction.11Similarly,Casalotti et al.12used periodic nonlinear absorbers for multimode vibration absorptions of a metamaterial beam.In addition,Song et al.13designed a metamaterial sandwich panel with periodically attached resonators for vibration and sound reduction.Li et al.14proposed a sandwich-like plate with massbeam resonators for vibration suppression and the results showed good control performance.Hu et al.15investigated a graded metamaterial beam for broadband vibration suppression.The obtained results revealed the effects of the frequency spacing and damping ratio on its performance.The study of Fang et al.16,17showed the ultra-broad band gaps of nonlinear metamaterials by inducing chaotic motions.The abovementioned studies demonstrated that,using the concept of metamaterial structure,the structure with periodic subunit design could achieve the vibration suppression over a wide band.

As demonstrated by the aforementioned studies,the design of metamaterial structures has seldom been used for the passive control of nonlinear aeroelastic system.Therefore,the objective of the present work is to provide a technique for supersonic flutter control of plate with the concept of metamaterial structure.A metamaterial plate is designed by embedding unit cells,say,periodic nonlinear resonators,for improvement of flutter and nonlinear aeroelastic behaviors.Moreover,we also propose an optimization strategy of parameters for designed unit cells to achieve the desirable passive control performance.

2.Nonlinear metamaterial plate model

We proposed a metamaterial plate coupled with a periodic array of unit cells (local nonlinear resonators),as shown in Fig.1.The length,width and thickness of the plate are denoted bya,bandh,respectively.Each unit cell,attached on one side of the plate,consists of a small massmj,dampercj,linear stiffnesskl,jand nonlinear stiffnessknl,j.For comparison,the total mass of unit cells is kept constant for different number of unit cells.In addition,the spaces between local resonators and plate are assumed to be large enough so that the local resonators do not collide with the plate during motion.Thus,the displacementspj(j=1,2,...,NR) are introduced as transverse motions ofNR(=nR×nR) unit cells.

Fig.1 Schematic diagram of metamaterial plate.

Based on the First-order Shear Deformation Theory(FSDT),the displacement components for the plate in thex,yandzdirections can be written as:

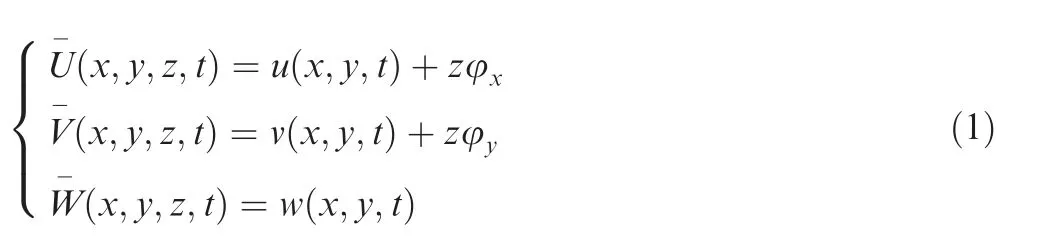
whereu,v,andwdenote the displacements on the middle surface of the plate in thex,y,andzdirections,respectively.φxand φydenote the rotations of the transverse normal to the middle surface about theyandxaxes,respectively.

According to the von Karman large deformation assumption using FSDT,the strain–displacement relations of the plate are given as18:

In Eq.(2),the stain vector can be divided into linear and nonlinear parts,

The constitutive relation of the plate structure is expressed as

whereσandεdenote the stress and strain vectors,respectively,Ddenotes elastic constant matrix.

The external work done by the aerodynamic pressure can be obtained by

where the linear stiffnesskl,jof local resonators can be rewritten asHere,ωR,jdenotes the resonance frequency of the corresponding derived linear resonators.

The Rayleigh’s dissipation function of the metamaterial plate is described as

Using the Rayleigh-Ritz approach,the displacement components of the plate can be obtained.19Then,substituting Eqs.(5)–(8) into the Hamilton principle,

Thus,the governing equations of the present metamaterial plate can be obtained as:

whereM,CandKdenote the mass,damping and stiffness matrices of the metamaterial plate,respectively.qsandqaare the generalized coordinate vector of the plate and displacement vector of resonators,respectively.FNLis the nonlinear restoring force term,andQis the generalized aerodynamic force.The linear flutter behavior of the metamaterial plate is obtained by solving the eigenvalue problem of Eq.(10),and nonlinear aeroelastic responses are solved by using Newmark integration technique combined with Newton-Raphson iterative scheme.18

To explore the energy transfer and passive suppression performance of the present metamaterial plate,several quantities(e.g.,the input energy by the airflow,dissipated energy and the total mechanical energy remained in the plate) are assessed by using the energy-based analysis approach.

The input energy by the airflow and dissipated energy fort∊[0,T] are obtained as

3.Results and discussion

In this section,the supersonic flutter control of the metamaterial plate is evaluated.A simply supported plate is made by aluminum alloy with material properties:Em=71.7 GPa,ρm=2700 kg/m3,υ=0.3.The geometrical parameters of the plate area=b=1.0 m,h=0.02 m.The flight condition is selected asMa=3.0,ρ∞=1.226 kg/m3.By neglecting the nonlinear restoring forceFNLand solving the eigenvalue equation of Eq.(10),the complex eigenvalue can be obtained as Ω=ΩR+iΩI,in which ΩIand ΩRare the imaginary and real parts of eigenvalue,respectively.As shown in Fig.2,the critical flutter aerodynamic pressure of the pure plate is λcr=513.3.The flutter is caused by the coupling between 1st and 2nd modes.For the metamaterial plate,variations of critical flutter aerodynamic pressure λcrand flutter frequencyfcrwith the resonance frequency ωR,jof local resonators for different number of unit cells are shown in Fig.3.The damping coefficientcj=0.02,the total mass ratio is kept asand this total mass is equally distributed to these resonators.It can be found that the resonance frequency of linear resonators between the 1st and 2nd modes of plate can enhance the flutter stability for all the cases.Moreover,with the increase of number of unit cells,the metamaterial plate has better aeroelastic behaviors.It can be seen from Fig.3(a)that the linear flutter boundary for the metamaterial plate with 10×10 unit cells is close to that for 8×8 unit cells.Hence,the use ofNR=8×8 can achieve the improvement of flutter stability for the present metamaterial plate.As shown in Fig.3(b),there is a sudden change at cutting point for the variation of flutter frequency for all the cases of number of unit cells.It can be divided into two regions for a further discussion.

Fig.2 Linear flutter behaviors of the pure plate.

Fig.3 Variations of critical aerodynamic pressure and flutter frequency with resonance frequency of local resonators for different number of unit cells.

Fig.4 presents the flutter behaviors of the metamaterial plate for ωR,j=9.66 and ωR,j=12.11,which are considered as typical cases of Region I and Region II,respectively.For the case of ωR,j=9.66,the coupling of the resonator mode and 2nd mode of the plate induces the flutter instability at λcr=533.8,where the resonator mode is destabilized with the increase of λ and the corresponding flutter frequency isfcr=13.75.For the case of ωR,j=12.11,the flutter instability of the system is produced by the coupling between the 1st mode of the plate and the resonator mode,and the coupled resonator mode destabilizes at λcr=524.4.The results demonstrate that the change in ωR,jof local resonators affects the coupled modes of the system flutter,and the flutter frequency of the unstable resonator mode is also markedly altered.Additionally,the present metamaterial plate can achieve a maximum of 8.24% flutter boundary increase.

Fig.4 Linear flutter results of the metamaterial plate with 8×8 unit cells.

Then,the nonlinear aeroelastic responses of the metamaterial plate are examined by using Newmark integration technique combined with Newton-Raphson iterative scheme.Fig.5 shows the bifurcation diagrams of nonlinear aeroelastic responses of the pure plate and metamaterial plate,where each unit cell has the same parameters.Here,the bifurcation diagrams are plotted with respect to a typical point (x,y)=(0.75a,0.5b) of the plate and dynamic pressure increment is Δλ=2.It is clearly seen that the design of the metamaterial plate can significantly influence dynamic bifurcation behavior of the plate.It can be found that the nonlinear aeroelastic responses of the metamaterial plate can be suppressed effectively in the region of λ<800.In this region,the metamaterial plate exhibits a random-like responses with smaller amplitude.As shown in Fig.6(a),the response of plate is reduced by up to 75%,and the amplitude of 52th unit cell (x52=13/16,y52=7/16)is far larger than that of plate,which indicates that the targeted energy transfers of local nonlinear resonators are activated by recurrent transient resonance capture.Using Eqs.(11)-(13),the energy analysis results can be obtained in Fig.6(b).It shows a dynamic balance between the input and dissipation of energy.It can also be seen that a great deal of energy transmission takes place in the region of λ<800 for the metamaterial plate.Nevertheless,the suppression effect of nonlinear aeroelastic responses become not obvious with the further increase of dynamic pressure (λ>800).Due to the same set of parameters used for unit cells in the previous cases,a modified design strategy and parametric optimization for unit cells are proposed in the following analysis to improve the passive control performance of the metamaterial plate.

Fig.5 Bifurcation diagram in terms of local amplitude extreme for the metamaterial plate.

Fig.6 Nonlinear aeroelastic responses of metamaterial plate at λ=600.

Fig.7 shows the design of the metamaterial plate with different set of unit cell arrays.As shown in Fig.7,there are four sets of parameters for unit cells by color,which should be determined by optimization design.We firstly choose the expected dynamic pressure λe,and then determine the optimization variables and objective.The linear and nonlinear stiffness coefficients both play key roles in suppression of flutter and nonlinear dynamic responses.In addition,the total mass of unit cells keeps constant and each unit cell has the same mass in order to have a common base for the comparison.Thus,the linear and nonlinear stiffness coefficients of the four sets of unit cells are set as design variables and we define the objective function as minimizing the amplitude of nonlinear aeroelastic responses at λe=1000.A hybrid pattern search optimization method20is adopted to obtain the optimal design parameters.

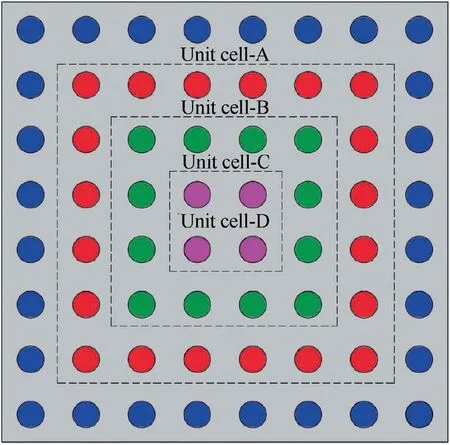
Fig.7 Modified design of metamaterial plate with different set of unit cell arrays.

Fig.8 shows the optimization process of the metamaterial plate using the hybrid pattern search method and the corresponding optimal parameters of unit cells are listed in Table 1.Clearly,the resonance frequencies corresponding to four sets of the derived linear resonators are located between the first two modes of the metamaterial plate,which can lead to an enlarged flutter boundary.The optimal amplitude of nonlinear dynamic response at expected dynamic pressure can be found at 75 iteration.It can be seen that the amplitude of plate at λe=1000 is reduced from 1.21 to 0.53 after optimization.Using the optimal parameters from Table 1,the dynamic bifurcation behavior of the metamaterial plate is compared with that of the pure plate in Fig.9.It is obvious that the amplitude of nonlinear aeroelastic responses for the optimized metamaterial plate can be controlled to a lower level.It should be noted that more than 55%reduction of response amplitude in the region of high dynamic pressure still can be accomplished.It indicates that the passive control performance does not degrade with the increase of dynamic pressure and more significant geometric nonlinear effect.

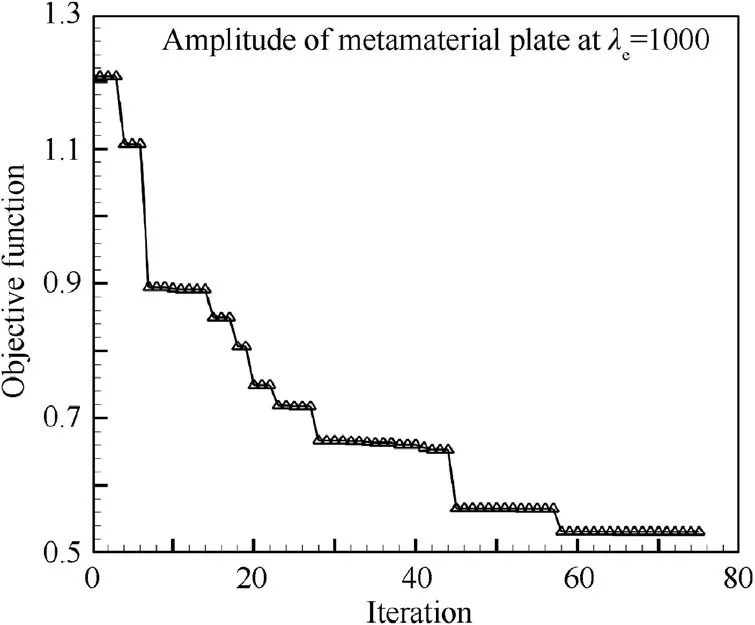
Fig.8 Optimization process of metamaterial plate by using hybrid pattern search method.

Table 1 Optimal parameters of unit cells in the design of metamaterial plate.

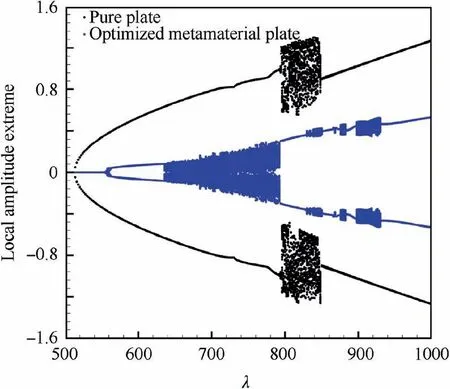
Fig.9 Bifurcation diagram in terms of local amplitude extreme for optimized metamaterial plate.

The above brief discussion indicates that the proposed parametric optimization strategy can achieve an enhanced suppression performance in terms of flutter and nonlinear aeroelastic responses.Furthermore,the present study demonstrates that the design of metamaterial plate can provide an effective approach for nonlinear flutter suppression of supersonic plate.

4.Conclusions

A metamaterial plate is designed by embedding periodic nonlinear resonators for its supersonic flutter control.The mathematical model of the metamaterial plate is established by the using the von Karman large deformation theory and supersonic piston theory of aerodynamics.The numerical examples show that the distributed nonlinear resonators can change the critical flutter modes and a proper stiffness value of local resonators can significantly enhance flutter stability.The phenomenon of recurrent transient resonance capture is found,and it is the mechanism of passive flutter suppression for the proposed metamaterial plate.Furthermore,we present a modified design strategy of the metamaterial plate and then perform a parametric optimization by using the hybrid pattern search algorithm.A significant enhancement of passive flutter control can be achieved by using of the optimal design parameters of unit cells,and its suppression performance does not degrade with the increase of dynamic pressure.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This study was supported by the National Natural Science Foundation of China (No.11972296) and the Overseas Expertise Introduction Project for Discipline Innovation,China(111 Project,No.BP0719007).