A Poisson multi-Bernoulli mixture filter with spawning based on Kullback–Leibler divergence minimization

Zhenzhen SU,Hongbing JI,Yongquan ZHANG

School of Electronic Engineering,Xidian University,Xi’an 710071,China

KEYWORDS Kullback–Leibler Divergence;Multi-target tracking;PMBM filter;Poisson Point Process;Random finite set;Target spawning

Abstract In the classical form,the Poisson Multi-Bernoulli Mixture(PMBM)filter uses a PMBM density to describe target birth,surviving,and death,which does not model the appearance of spawned targets.Although such a model can handle target birth,surviving,and death well,its performance may degrade when target spawning arises.The reason for this is that the original PMBM filter treats the spawned targets as birth targets,ignoring the surviving targets’information.In this paper,we propose a Kullback–Leibler Divergence (KLD) minimization based derivation for the PMBM prediction step,including target spawning,in which the spawned targets are modeled using a Poisson Point Process (PPP).Furthermore,to improve the computational efficiency,three approximations are used to implement the proposed algorithm,such as the Variational Multi-Bernoulli (VMB) filter,the Measurement-Oriented marginal MeMBer/Poisson (MOMB/P) filter,and the Track-Oriented marginal MeMBer/Poisson (TOMB/P) filter.Finally,simulation results demonstrate the validity of the proposed filter by using the spawning model in these three approximations.

1.Introduction

Multi-Target Tracking (MTT) is concerned with estimating the number and states of targets in the presence of target appearance uncertainty,detection uncertainty,clutter,and data associations.It has been widely used in many applications such as defense,1–4robotics,5–7aviation,8–11and cell biology.12,13The primary solution paradigms for MTT include the Multiple Hypothesis Tracking (MHT),14the Joint Probabilistic Data Association (JPDA) filter,15and the Random Finite Set (RFS) filters.16,17Since the multi-target Bayes filter can obtain an optimal estimation within RFS theory,RFS filters play a critical role in MTT.

In the early stage,several approximations of the multitarget Bayes filter have been proposed,such as the Probability Hypothesis Density (PHD) filter,18the Cardinalized PHD(CPHD) filter,19the Multi-target Multi-Bernoulli (MeMBer)filter,16and the Cardinality-Balanced MeMBer (CBMeMBer)filter.20Although the filters above can avoid the combinatorial explosion problem in the data association,their tracking accuracy is low due to the approximations in the Bayes recursion.Relatively new research is focused on the conjugate prior,which means that the prior distribution has the same form with the posterior distribution.The conjugate distribution in multitarget Bayes filter is a significant trend because it can provide more accurate approximations to the actual posterior distribution.

Conjugate prior based filters have been proposed based on labeled RFS and unlabeled RFS.For labeled RFS,the Generalized Labeled Multi-Bernoulli (GLMB) filter was proposed using the labeled multi-Bernoulli conjugate prior.21,22For unlabeled RFS,the Poisson Multi-Bernoulli Mixture(PMBM) filter was proposed using the PMBM conjugate prior,in which the unknown targets were modeled using a Poisson Point Process (PPP),and the surviving targets were modeled using a Multi-Bernoulli Mixture (MBM).23The PMBM filter solves the unlabeled multi-target Bayes filer in exact closed form.Therefore,the PMBM is a more efficient filter structure than the GLMB filter.24Some existing simulation results have shown that the PMBM filter outperforms the GLMB filter for both point target tracking and extended target tracking.24,25Besides,emerging research is the distributed/multi-sensor PMBM filter,which significantly promotes the PMBM filter application in wireless sensor networks.26–28

However,the PMBM filter exhibits lower performance when the target spawning arises.The reason for this is that the original PMBM filter considers the spawned targets as birth targets on their first occurrence.In fact,the spawned targets are dependent on the surviving targets,but the birth targets are not.At the same time,the Kullback–Leibler Divergence(KLD)minimization is widely used in RFS theory to design many effective filters.29–33Subsequent to our conference publication,34a new filter based on the PMBM density that formally incorporates spawning is proposed based on KLD minimization in this paper.Firstly,the spawned targets generated by each surviving target are modeled using a PPP,which guarantees the efficiency of the filter structure.Under such a spawning model,the multi-target prediction density is no longer a PMBM density,even if the initial prior follows a PMBM distribution.Secondly,in order to derive a trackable filter,the multi-target prediction density is approximated by a PMBM density based on KLD minimization.Thirdly,due to the intractability of the PMBM filter,the PMBM with target Spawning (PMBMS) is implemented using three PMBM approximations,such as the Variational Multi-Bernoulli(VMB) filter,the Measurement-Oriented marginal MeMBer/Poisson (MOMB/P) filter,and the Track-Oriented marginal MeMBer/Poisson (TOMB/P) filter.Finally,simulation results show that the VMB,MOMB/P,and TOMB/P filters with spawning outperform the original filters when target spawning arises.

The rest of this paper is organized as follows.In Section 2,the theoretical foundation of RFSs,multi-target Bayes filters,and KLD is reviewed.Then,the PMBM filter with spawning and its implementation are proposed in Section 3.Section 4 presents the simulation results.Subsequently,the conclusion is drawn in Section 5.

2.Background

This section provides a brief review of RFSs,multi-target Bayes filter,and KLD pertinent to the formulation of our multi-target tracking problem.

2.1.Random finite sets

The PMBM filter utilizes two basic forms of RFS distribution,known as PPP and Bernoulli process.

2.1.1.Poisson Point Process

For an arbitrary RFS densityg(X),its intensity function is defined as16

where λ(x) is the intensity function offppp(X).Xis with Poisson distributed cardinality,in which all elements are independent and identically distributed.

2.1.2.Bernoulli process

A Bernoulli RFS is empty with probability 1-ror a single element with probabilityrwhose Probability Density Function(PDF)isp(x).A Bernoulli density with probability of existencerand PDFp(x) can be defined as

2.1.3.Multi-Bernoulli process

A Multi-Bernoulli(MB)RFS is a unionof a fixed number of independent Bernoulli RFSsXi.An MB density can be defined as

wherefi(Xi) is the Bernoulli density with probability of existenceriand PDFpi(x).is the disjoint set union,i.e.,given RFSX,YandW,means thatX∪Y=WandX∩Y=Ø.

2.1.4.Multi-Bernoulli mixture

A Multi-Bernoulli Mixture (MBM) density is a linear combination of some MB densities,which can be given by

whereJis the number of the MB densities in the MBM density andwiis the normalized weight of theith MB density.

2.1.5.Poisson multi-Bernoulli mixture

A PMBM density is a linear combination of independent PPP and MBM components,which can be given by

2.2.Multi-target Bayes filter

In RFS filters,the multi-target transition model and measurement model in the multi-target Bayes filter are as follows.

2.2.1.Transition model

2.2.2.Measurement model

The multi-target measurement modelis to describe the multi-target measurementZkat timekgenerated by given target states,including the detections and false alarms.A target with statexkis detected with probabilitypd(xk)and generates a measurementzkwith likelihoodg(zk|xk),or missed with probability 1-pd(xk).It is assumed that the measurements inZkare mutually independent.The false alarms at each time appear according to a nonhomogeneous PPP with intensity λfa(z),which are independent of measurements generated by the targets.

2.2.3.Bayes recursion

An analytic solution to the Bayes recursion is presented,known as the PMBM filter.23In the PMBM filter,the multitarget stateXcan be divided into the unknown target statesXuand the detected target statesXd,which can be written as

Then,the posterior multi-target PDF is modeled as a PMBM density,in which the PPP and MBM densities describe the distribution of the unknown targets and the detected targets,respectively.Thus,the posterior PMBM density is expressed as

wherefppp(∙) is a PPP density with intensity λu(x) describing the unknown targets,fmbm(∙) is an MBM density describing the detected targets,nis the number of the components inXd,andNis the number of the tracks in each MB density.Ais the set of the global association history hypotheses,which can be expressed as

whereaiis the index of the hypothesis utilized for tracki,Mi,aiis the history of the measurement indices corresponding to tracki,hiis the hypothesis number of tracki,andMis the set of all measurement indexes up to and including the present time.is the global hypothesis weight,satisfying

2.3.Kullback–Leibler divergence

KLD is a measure of how one distribution is different from a second,reference distribution.For RFS densitiesf(X) andg(X),the KLD is defined to be the set integral

The following theorem shows the minimization of KLD for the Poisson RFS.

Theorem 1.Suppose that f(X)is an RFS density and g(X)is a Poisson density with intensity functionλ(x).Then,the intensity functionλ(x)minimizes the KLDD(f|g)satisfyingλ(x)=Df(x),where Df(x)is the intensity function of f(X).

Theorem 1 has been proved.30

3.PMBM filter with spawning

This section presents a spawning model for the PMBM density and a trackable multi-target filter for such a spawning model.

3.1.Spawning model

The schematic diagram of the PMBM filter is shown in Fig.1.In the prediction step,the predicted PPPis obtained involving the surviving hypotheses of the previous unknown targets and the birth hypotheses,while the predicted MBMincorporates the surviving hypotheses of the detected targets.In the update step,the updated PPPincludes the undetected hypotheses of the unknown targets,while the updated MBMis obtained involving the detected and undetected hypotheses of the previous detected targets,and the birth hypotheses of the previous unknown targets.

Fig.1 Schematic diagram of PMBM filter.

In the PMBM filter,the detected targets are generally more important than the unknown targets.The reason for this is that the detected targets are hypothesized to exist and have been detected before.In contrast,the unknown targets are hypothesized to exist but have never been detected.These unknown targets can be detected after the birth targets occur in the surveillance region.Therefore,the detected targets are modeled using an MBM density with high estimation accuracy.In contrast,the unknown targets are modeled using a PPP density with lower computational complexity and estimation accuracy.

The original PMBM filter can estimate the states of the spawned targets by treating them as birth targets.However,the spawned targets are different from the birth targets.This is because the spawned targets are separated from the surviving targets,which are related to the surviving targets,but the birth targets are not.Although the spawned targets can be tracked by considering them as birth targets,the surviving targets’information is neglected in the process.Such an operation degrades the performance of the PMBM filter when target spawning arises.In order to improve the performance of the PMBM filter,target spawning should be considered additionally.

The spawned targets are similar to the birth targets,which can be detected after target spawning occurs in the surveillance region.One strategy of modeling the spawned targets is to use the Bernoulli processes,while the other strategy is to use the PPP.If the spawned targets are modeled using the Bernoulli processes,the number of MB’s components after the prediction step will beNk|k-1=2Nk-1|k-1,which results in an exponential increase in the complexity of the PMBM update.If the spawned targets are modeled using the PPP,the number of the unknown target components after the prediction step will bewhich can be neglected compared with the former model.In order to estimate the states of the spawned targets with low computational complexity,we propose a target spawning model based on the PPP in this work,which is given under the following assumption.

3.2.Multi-target tracking with spawning

The schematic diagram of the PMBMS filter is shown in Fig.2.In the prediction step,the spawning hypotheses of the previous detected targets are added into the predicted PPPThen,the spawning hypotheses are captured into the updated MBMduring the update step.

Fig.2 Schematic diagram of PMBMS filter.

Since the predicted multi-target density is not a PMBM density without any approximations,the updated multitarget density is also not a PMBM density.The strategy of using the PMBM density to track spawning targets is to approximate the multi-target density by a PMBM density.Thus,a PMBM approximation is performed on the predicted multi-target density to reduce information loss based on the KLD minimization.Then,the PMBMS remains to maintain a closed-formed recursion in which a PMBM density is recursed over time.Based on this,the prediction and update steps of the PMBMS filter are given by the following two propositions.

Proposition 1.Given the posterior PMBM density at time k-1as

Proof of Proposition 1.According to the PMBM density(Eq.(11))and the prediction step(Eq.(8)),the predicted PMBM density is obtained by

Then,we will obtain a PMBM density,which minimizes the KLD with the density in Eq.(37).Since the spawning targets are modeled using a PPP density,the PPP density of the PMBM density should be used to describe all the birth targets and spawned targets.

Following the application of Lemma 1,fk|k-1(Xk) can be approximated based on KLD minimization as follows:

The existing hypothesesai=2,in whichai=2 denotes the birth hypothesis or the spawning hypothesis,are given by

The proof of Proposition 2 is the same as that of the update step of the PMBM filter.23

3.3.Efficient implementation

The previous subsection derived the PMBMS filter.However,the filter is intractable.Meanwhile,the PMBM filter has an obstacle that it is theoretically impossible to prune the PMBM distributions.37The reason for this is that pruning one or more MB densities of an MBM density does not affect the symmetry of the MBM density as each of the terms in the mixture is an MB density,which is symmetric.However,pruning the individual terms of one MB density is not permissible as the pruning of the MB density affects the symmetry of the MB density.37Thus,approximations must be made.There are mainly three implementation methods for the PMBM filter by approximating the MBM density of a posterior PMBM density as a single MB density,known as the VMB,MOMB/P,and TOMB/P filters.

It should be noted that the Poisson Multi-Bernoulli with Spawning (PMBS) recursion is a particular case of the PMBMS filter.34This is due to the fact that the prediction and update steps in the previous subsection can be simplified as the prediction and update steps of the PMB filter when the posterior PMBM density is approximated as an MB density.

Although the VMB filter can provide the most accurate target state estimation in these three filters,its computational burden is higher than the other two filters.Besides,the MOMB/P filter has better performance than the TOMB/P filter when the coalescence occurs.The TOMB/P filter exhibits higher performance than the MOMB/P filter when the targets are wellspaced.

In the simulation,these three filters are used to implement the PMBMS filter,respectively.The TOMB/P and VMB filters output the estimates for all tracks with the existence probability higher than 0.7,while the MOMB/P filter outputs the estimates for the corresponding number of tracks with the highest probability of existence.

4.Simulation

In this section,the results from a Monte Carlo simulation study are presented.The VMB,MOMB/P,and TOMB/P with spawning are denoted by the VMBS,MOMB/PS,and TOMB/PS,which are compared with the VMB,MOMB/P,and TOMB/P filters,respectively.

4.1.Parameter setting

Two challenging scenarios are used to verify the performance of the proposed filter.The true trajectories are shown in Fig.3.In the first scenario,as shown in Fig.3(a),the number of targets varies in a [-100,100]m×[-100,100]m surveillance region because of target surviving,birth,death,and spawning.During the 100 time steps,targets 1,2,and 3 are born at times {1,31,61} and generate generation spawns at times {11,41,71},respectively.Then,targets 1 and 2 die at times {50,85},respectively.In the second scenario,as shown in Fig.3(b),the number of targets varies in a[-150,150]m×[-150,150]msurveillance region because of target spawning.During the 200 time steps,targets 1,2,and 3 generate three generation spawns at times {40,100,160},respectively.The second scenario is more complicated than the first scenario because these targets move with a process noise in the second scenario.

Fig.3 Target trajectories.

where the sampling periodTis set to be 1s andq=0.01.I2×2and ⊗denote a 2×2 identity matrix and Kronecker product,respectively.In this work,the cases withare considered.pd=0.99 means that these targets can be detected well by the sensor,whilepd=0.80 means that the sensor cannot detect these targets well.Each target is observed with a Gaussian noise model

whereH=[1,0]⊗I2×2.

The initial unknown target intensity is assumed to be λb(x)=10N(x;0,P) withP=diag[1002,1,1002,1].In the first scenario,thebirth intensity of the original PMBM filter is assumed to be λb(x)=0.06N(x;0,P),which means that six targets are expected to arrive in the 100 time steps on average.Meanwhile,the birth intensity and spawning intensity of the proposed PMBM filter are assumed to be λb(x)=0.015N(x;0,P) andrespectively,which means that three targets are expected to arrive and each target generates one generation spawn in the 100 time steps on average.In the second scenario,the birth intensity of the original PMBM filter is assumed to be λb(x)=0.06N(x;0,P).The birth intensity and spawning intensity of the proposed PMBM filter are assumed to be

The average number of the false alarms λfaat each time step is set to be 10 and 30,respectively,which are uniformly distributed on the surveillance region.λfa=10 means that the false alarms distribute sparsely in the surveillance region with false alarm rate 1×10-3m-2,while λfa=30 means that the false alarms distribute densely in the surveillance region with false alarm rate 3×10-3m-2.

In order to evaluate the performance of the proposed filter,the Optimal Sub-Pattern Assignment (OSPA) distance40is adopted,which is defined as

whereX={x1,x2,∙∙∙,xm} andY={y1,y2,∙∙∙,yn} are finite subsets.Πkdenote the set of permutations on {1,2,∙∙∙,n}for any positive integerk.pandcare set to be 1 and 50,respectively.The simulations are implemented by MATLAB 2019b on Inter Core i9-9900 3.10 GHz processor and 16 GB RAM.To verify the validation of the proposed filters,200 Monte Carlo trails are performed.

4.2.Simulation results

4.2.1.VMB with spawning

The OSPA distance and cardinality estimate for the VMBS and VMB filters in the scenario one withpd=0.99 are shown in Fig.4 when the average number of the false alarms λfais 10 and 30.From Fig.4,it can be seen that the VMBS filter has a smaller error and adapts to the target number changes faster than the VMB filter when target spawning occurs at times{11,41,71}.This is due to the fact that the spawning model of the VMBS filter can immediately capture the spawned targets after target spawning occurs.From Figs.4(c) and (d),it shows that the spawning model promotes the tracking performance more with larger λfa.Simultaneously,the VMBS filter almost has the same performance with the VMB filter,when the target birth and death occur.

Fig.4 Performance of VMBS and VMB filters in scenario one when pd=0.99.

The OSPA distance and cardinality estimate for the VMBS and VMB filters in the scenario one withpd=0.80 are shown in Fig.5 when the average number of the false alarms λfais 10 and 30.From Fig.5,it can be seen that the VMBS filter still has better tracking performance than the VMB filter when target spawning occurs at times{11,41,71}.Although the VMBS and VMB filters have larger errors and adapt to the target number changes slower with lower detection probability,they are both suitable for the low detection probability.Meanwhile,the spawning model also promotes the tracking performance more with lowerpd.

Fig.5 Performance of VMBS and VMB filters in scenario one when pd=0.80.

Besides,because the number of the targets tends to increase during the 100 time steps and the OSPA metric can obtain the average estimation error of each target,the OSPA distance tends to drop if only one target is lost in the tracking process.For example,the OSPA distance at time 11 is higher than that at time 41.The reason for this is that one of the two targets is lost at time 11,while one of the four targets is lost at time 41.

The OSPA distance and cardinality estimate for the VMBS and VMB filters in the scenario two withpd=0.80 and λfa=10 are shown in Fig.6.It can be seen that the VBMS filter has better performance than the VMB filter in the complex scenario,especially when target spawning occurs.

Fig.6 Performance of VMBS and VMB filters in scenario two when pd=0.80 and λfa=10.

4.2.2.MOMB/P with spawning

The OSPA distance and cardinality estimate for the MOMB/PS and MOMB/P filters in the scenario one are shown in Figs.7 and 8 whenpdis 0.99 and 0.80,respectively.The OSPA distance and cardinality estimate for the MOMB/PS and MOMB/P filters in the scenario two withpd=0.80 and λfa=10 are shown in Fig.9.From Figs.7–9,it can also be seen that the MOMB/PS filter has better tracking performance than the MOMB/P filter when target spawning occurs.They are both suitable for low detection probability and complex scenario.

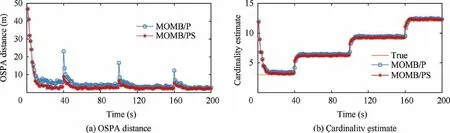
Fig.9 Performance of MOMB/PS and MOMB/P filters in scenario two when pd=0.80 and λfa=10.

Fig.7 Performance of MOMB/PS and MOMB/P filters in scenario one when pd=0.99.

It should be noted that the OSPA distance of the MOMB/P filter becomes smaller in Fig.8 when target spawning occurs.The reason for this is that the lower detection probability increases the weight of the undetected hypothesis.At this time,the spawned targets on their first occurrence may be associated with the measurement of the nearby surviving targets.Additionally,since the probabilities of existence in each Bernoulli component are both with small value at the beginning,the corresponding number of tracks with the highest probability of existence is with a significant bias at these time steps.Thus,the MOMB/PS and MOMB/P filters have significant error at the beginning.

Fig.8 Performance of MOMB/PS and MOMB/P filters in scenario one when pd=0.80.

4.2.3.TOMB/P with spawning

The OSPA distance and cardinality estimate for the TOMB/PS and TOMB/P filters in the scenario one are shown in Figs.10 and 11 whenpdis 0.99 and 0.80,respectively.At the same time,the OSPA distance and cardinality estimate for the TOMB/PS and TOMB/P filters in the scenario two withpd=0.80 and λfa=10 are shown in Fig.12.From Figs.10–12,it can also be seen that the TOMB/PS filter has the same advantages as the MOMB/PS filter compared with the TOMB/P filter.They are both suitable for low detection probability and complex scenario.

Fig.12 Performance of TOMB/PS and TOMB/P filters in scenario two when pd=0.80 and λfa=10.

Compared with the MOMB/PS filter,the TOMB/PS filter adapts to the target number changes slower when target spawning occurs.This is due to the fact that the TOMB/PS filter suffers from the coalescence,which adopts the idea of data association methods.However,the MOMB/PS filter has lower performance than the TOMB/PS filter,when the targets are well-spaced.It should be noted that the VMBS filter can overcome the disadvantages of the MOMB/PS and TOMB/PS filters.

The average runtime of a single Monte Carlo trial and the cardinality bias of the VMBS,VMB,MOMB/PS,MOMB/P,TOMB/PS,and TOMB/P filters in the scenario one are given in Table 1 withpd=0.99.It can be seen that the computation efficiency of the VMBS,MOMB/PS,and TOMB/PS filters is slightly slower than that of the VMB,MOMB/P,and TOMB/P filters,respectively.However,their difference in computation efficiency can be negligible,which is not apparent.Although the VMBS filter has better tracking performance than the MOMB/P and TOMB/P filters,the computational burden is higher.

Table 1 Average runtime and cardinality bias of these filters in scenario one when pd=0.99.

Fig.10 Performance of TOMB/PS and TOMB/P filters in scenario one when pd=0.99.

Fig.11 Performance of TOMB/PS and TOMB/P filters in scenario one when pd=0.80.

Fig.13 shows the tracking performance of these filters for various numbers of false alarms in the scenario one whenpdis 0.99.It can be seen that the average OSPA gap between the VMBS and VMB filters increases as λfaincreases.The average OSPA gap between the MOMB/PS and MOMB/P filters also increases as λfaincreases.The average OSPA gap between the TOMB/PS and TOMB/P filters increases slightly as λfaincreases.Fig.14 shows the tracking performance of these filters for various values of detection probability in the scenario one when λfais 10.It can be seen that the average OSPA gap between the VMBS and VMB filters decreases aspdincreases.The average OSPA gap between the MOMB/PS and MOMB/P filters also decreases aspdincreases.The average OSPA of the TOMB/PS and TOMB/P filters are quite close for a wide range ofpd.This is because the predicted PPP with spawning is more accurate to estimate the spawned target states.Furthermore,it can also avoid the generation of false tracks.In addition,the TOMB/PS and TOMB/P filters suffer from the coalescence whose tracking performance mainly depends on the influence between these targets.Thus,the spawning model has small influence on the TOMB/PS and TOMB/P filters when targets spawning occurs.

Fig.13 Average OSPA versus false alarms in scenario one when pd=0.99.

Fig.14 Average OSPA versus detection probability in scenario one when λfa=10.

Fig.15 shows the trajectories of the targets and the tracking result of a sample run,where the blue circles and the red points represent the estimation of the original filters and the proposed filters,respectively.It can be seen that the VMBS,MOMB/PS,and TOMB/PS filters can obtain less false targets than the VMB,MOMB/P,and TOMB/P filters,respectively.Simultaneously,the false targets of the MOMB/PS filter are more than those of the VMBS and MOMB/P filters.This is because the MOMB/P filter follows the philosophy of the MeMBer filter,which is sensitive to false alarms.

Fig.15 Ground truth trajectories of the targets and estimated trajectories in scenario two when pd=0.80 and λfa=10.

5.Conclusions

The motivation for the work presented in this paper is to solve the multi-target tracking problem in which the preexisting targets may generate generation spawns.To this end,a new PMBM filter considering target spawning is derived based on KLD minimization in which spawned targets are modeled by a PPP.The PMBM filter with spawning can take full advantage of the preexisting targets’ information to improve the tracking accuracy.Three approximations,known as the VMB,MOMB/P,and TOMB/P filters,are used to implement the new PMBM filter.Simulation results show that the proposed VMB and MOMB/P filters with spawning have betterperformance when target spawning occurs,especially in the challenging cases with lower detection probability or more false alarms.The VMB,MOMB/P,and TOMB/P filters with spawning can alleviate the generation of false targets.

The extended target spawning and group splitting problems are challenging because the data association in these problems is more complicated than that in multiple point target tracking.Possible future work includes how to solve the extended target spawning and group splitting problems based on the PMBMS recursion.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgement

This work was supported by the National Natural Science Foundation of China (No.61871301).