Simplification approaches for multi-level load spectra by using equivalent damage rule
Xiaohong LI,Qin SUN
School of Aeronautics,Northwestern Polytechnical University,Xi’an 710072,China
KEYWORDS Aircraft structure;Equivalent fatigue life;One loading block;Simplification approaches;Variable amplitude loadings
Abstract Reasonable and effective fatigue load spectrum is key of aircraft structural fatigue test.Two kinds of load spectra simplification approaches based on statistical consistent fatigue damage model are proposed in the paper.One method is to simplify the original multi-level load spectra to spectral load with fewer level and was verified by the experimental data of five levels and seven levels load spectra.The equivalent damage here is not equivalent fatigue life,but equivalent number of spectral blocks.Moreover,it was proved that a section of low stress load cannot be converted into the highest stress load considering equivalent damage.The other is to convert the life distribution under multi-level load spectra into that of constant amplitude spectrum according to a certain principle,that is,equivalent damage is achieved through equivalent fatigue life,and two groups of three levels spectral data were used for experimental verification.The results show that equivalent damage simplification approach of multi-level load spectra is feasible,and it achieve that the damage of one loading block before and after the simplification is equal in probability statistics.The life distribution of load simplified as constant amplitude spectrum is consistent with test data.The simplification method presented in this paper can be generalized and is a predictive engineering method which does not depend on experimental data.
1.Introduction
The used load spectrum in aircraft design is the basis of structural strength calculation,damage tolerance and durability analysis as well as test perform.In general,aircraft has a high number of flight hours,and the key parts of structure are designed as high-cycle fatigue according to durability.1–3The test verification of fatigue life for full-size structure is carried out directly in accordance with the standard load spectrum formed by the statistical specification of aircraft standard mission profile and the damage counting principle.Even if the two-fold life verification test is completed,the consumption of time and cost are huge.Therefore,the study of simplification methods for fatigue load spectrum has important engineering practical value for shortening experimental period and improving technical and economic benefits.
The premise of fatigue load spectrum simplification technique is to determine fatigue damage.Fatigue damage is a characteristic of the degradation of mechanical properties of aircraft components under various loads.Over the past few decades,a number of models have been exhibited on the fatigue damage theory of structures.4–9The early proposed method of using the Linear cumulative damage theory (Miner rule)10to do equal damage conversion has been widely applied.However,it is a linear and deterministic method without considering the sequential effect of load.11The model12–14pointed out later overcomes the shortcoming of Miner rule by using the coefficient of load interaction,and did not require material test.The numerical validation results of this model are not well consistent with the test,which leads to the limitation of its application.In addition,in recent decades,researchers have developed a series of damage models from damage evolution curve,15Continuous Damage Mechanics (CDM),16,17energybased method,18,19and based on the concept of crack propagation.20The above models did not take into account the statistical properties of cumulative damage in determining fatigue load damage.In,21a time-dependent double-scale probabilistic fatigue damage model was described.The reverse statistical inference method22was used to fit thep-S-Ncurve of fatigue to improve the prediction accuracy of small sample life data.The classic model was the statistically consistent fatigue damage model based on Miner criterion investigated by Sun.23It made a quantificationally accumulated calculation of engineering damage caused by every cycle load,which could be better applied to the prediction of fatigue damage under complex loads in engineering practice.This paper is a research based on the above model.
Aircraft usually is operated in a complex load environment,and the spectrum hours number of aircraft is far less than fatigue life.24–26The fatigue loading spectra of general flight is a random load or a random sequence of simple multi-level load cycles,among which small stress load cycles account for a large proportion and the damage caused by these loads for structure is relatively small compared with other load levels.27,28Moreover,the multi-level load spectra have great influence on the fatigue crack propagation life of acceleration test for whole aircraft.Therefore,it is an urgent problem for researchers to find an effective method to simplify multi-level load spectra.
So far,the existing simplified methods for load spectrum include low-load interception,29,30high-load acquisition,amplitude enhancement,and severity spectrum.31,32The influence of interaction and sequence effect of loading is often considered in the process of load spectrum simplification.33,34In view of the above simplification methods,the researchers put forward the simplification criteria of load spectrum,including the finite objective,the damage consistency and the damage equivalence,among which the damage equivalence criterion is the more commonly used in the estimation of fatigue life,compilation of fatigue load spectrum and simplification of load spectrum.35The equivalent damage principle of simplifying to adjacent large loads is adopted to minimize the number of loading cycles in each flight and thus shorten the test time.The approach of equivalent damage simplification be divided into:the original multi-level load spectra are simplified to the load blocks with fewer levels,and are converted to the load with constant amplitude.The key is that the concepts of these two types of equivalent damage are understood differently,which lead to different simplification effects.The rule of equivalent damage for constant amplitude spectrum is the same fatigue life,it is different for load spectrum with fewer levels.The existing simplified method for fewer-level load spectra was as follows:the load with low stress level was removed,and the damage caused by low load was converted to the load with high stress level,so as to reduce the number of load cycles.This simplified method belongs to the accelerated fatigue test.36,37The difficulty lies in finding a definite method to make statistical properties of damage distribution caused by one loading block before and after simplification be the same,that is to ensure that the number of blocks before and after conversion is identical distribution when structure reached fatigue failure.However,the fatigue life of structure is the product of the number of loading blocks and loading hours number or the total cycles number of one loading block.As the total cycles number decreases after simplification,the corresponding life is shortened.
The purpose of this paper is that original multi-level load spectra is simplified to fewer-level load on the basis of equal number of loading blocks and to constant amplitude spectrum considering equivalent fatigue life.The remaining part of the paper as follows:We first put forward the simplified method that to reduce the lower stress level load in falling section to the highest stress level in the case of low–high-low sequential programming.Secondly,the feasibility of the method is verified by the test load spectrum,and the low stress load in rising section cannot be converted into high stress load with equivalent damage rule is proved.In addition,the simplification method from multi-level load spectra to constant amplitude spectrum was studied,and the results of five transformation criteria are compared.The approaches presented in this paper are effective for realization of equivalent damage simplification in engineering practice.
2.Methods
2.1.To simplify multi-level load spectra to fewer-level load spectra
Assuming the level number of original loading spectra are 2m+1.Where 1 represents the intermediate level with the highest stress,andmdefines the load level number with lower stress in rising and falling section.The load levels of the falling section are converted to the intermediate load level with the highest stress.In order to minimize the number of cycles,all low stress loads except level 1 (m+2 in the total level) in falling section are converted,i.e.all loads in the laterm-1 levels are converted to the intermediate level with highest stress.There are two purposes for retaining the level 1 in falling section:one is to ensure the feasibility of equivalent damage conversion.Because the stress of this level is relatively high,the damage caused by it takes up a larger proportion in total damage.The other is to maintain a low–high-low spectrum arrangement although the load is asymmetrical.In this way,the levels simplified load spectra are at leastm+2,and the arrangement order is asymmetrical low–high-low.In addition,the concept of equal damage here means that damage caused by one loading block before and after simplification is equal in statistical properties (mean and variance) and pass the Smirnov test.
2.1.1.Method of simplification to fewer-level load spectra
The multi-level load spectra are simplified to fewer-level load spectra by using equivalent damage rule.Firstly,the load level with too little fatigue damage is cut off,generally corresponding to the first level or the last level load.Then the load levels with lower stress are converted to with highest stress level.The detailed steps of the simplification approach are as follows:
Step1.The cycle-life rationi/Eifor each level is sorted and the maximum value is assumed to ben(1)/E(1).Theith load level satisfyingni/Ei<(n(1)/E(1))∙5% criterion is cut off,and the original order of remaining loads level does not change.
Step2.Assuming the number of cycles per level for multilevel load spectra (total level of 2m+1) isn1,n2,...,nm+1,...,n2m+1and corresponding damage isD1,D2,...,Dm+1,...,D2m+1.For simplicity,the last load level(2m+1) is converted to the maximum stress level (m+1)according to equivalent damage.So that equationbe satisfied,and the number of cycles of the highest stress level is increased fromnm+1toThe detailed solution process is as follows:
(1) The probability calculation model of fatigue damage of multi-level load spectra in Ref.23as shown in Eq.(1)was used to solve the damage caused by each level of load.This statistical model considers the load sequence effects of multi-level load spectra.In fatigue load spectra,the effect of hysteresis is smaller when the difference between high and low load levels is small.On the contrary,the effect is greater.The load level in falling section is affected by load hysteresis effect of the highest stress level.It is precisely because of hysteresis factor exp(-f)that the equivalent damage conversion can be achieved in the probability sense.
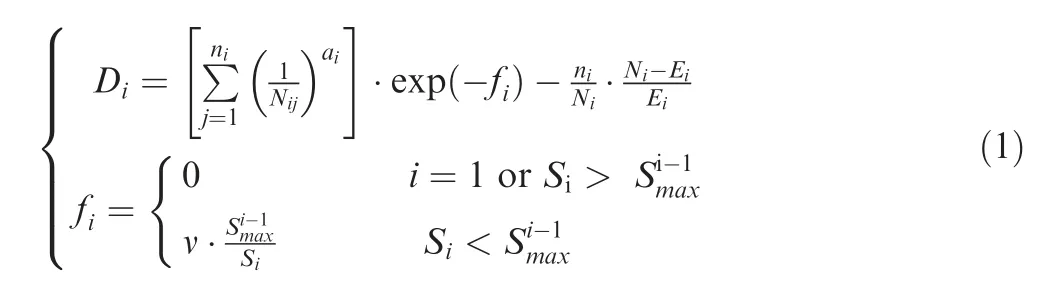
whereNijandNiare random fatigue life;Eiis expectation of fatigue life;nicycles;iload level;Difatigue damage of theith level;aiconsistent index;ficoefficient of hysteresis effect;Sistress amplitude;maximum stress from 1 toi-1 load level;vmaterial constant andv=2 for aluminum alloy.
The relevant parameters of load of level 2m+1 and levelm+1 were substituted into Eq.(1) for random sampling in 2000 groups,and then damage of the two levels in each group were added to obtain the damage data ofD2m+1+Dm+1with a maximum sample size.Maximum likelihood estimation was performed to obtain two damage distribution parameters of meanE0and standard deviation√----D0,with which the numerical sampling test would take the damage distribution as reference distribution.
(2)An appropriate number of cyclesis found by using dichotomy to make the damage distribution parameters caused by load in them+1 level of this cycle number approximately equal to the reference distribution parameters.The initial range of cycle numberis[a,b],whereais the original cycle number of levelm+1,that is,a=nm+1.bis determined by Miner equivalent damage criterion (Δnm+1/Sm+1)=(n2m+1/S2m+1),sob=nm+1+Δnm+1=nm+1+(Sm+1/S2m+1)∙n2m+1.

2.1.2.Smirnov test
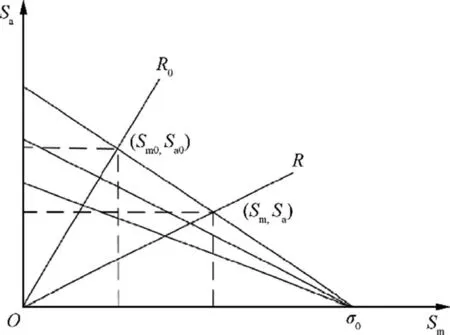
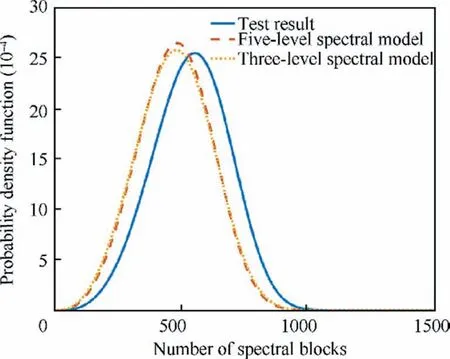
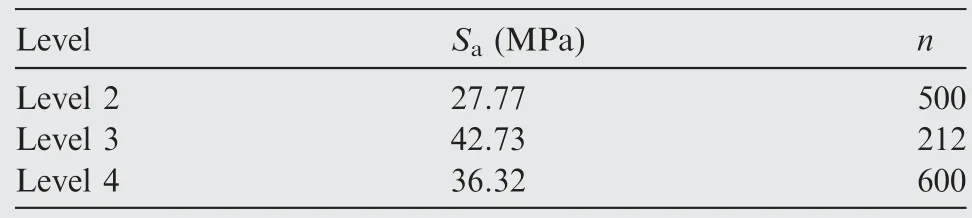
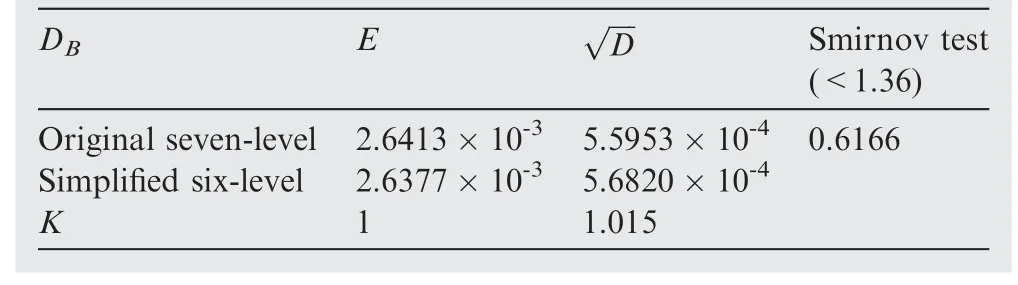
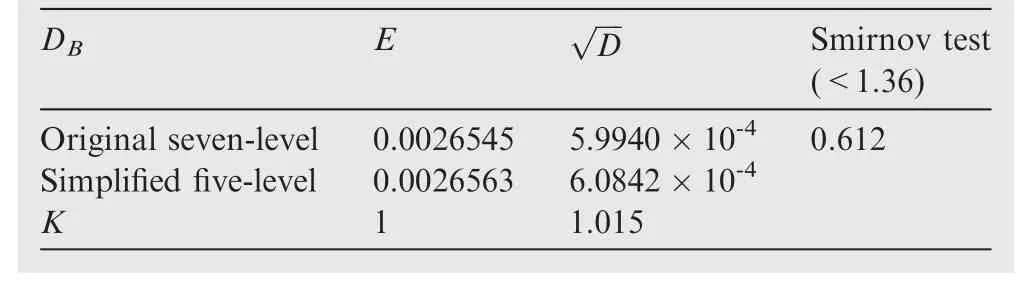
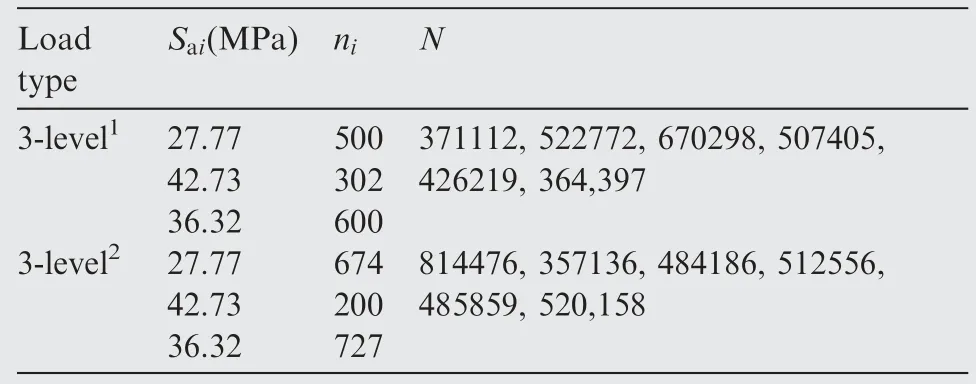
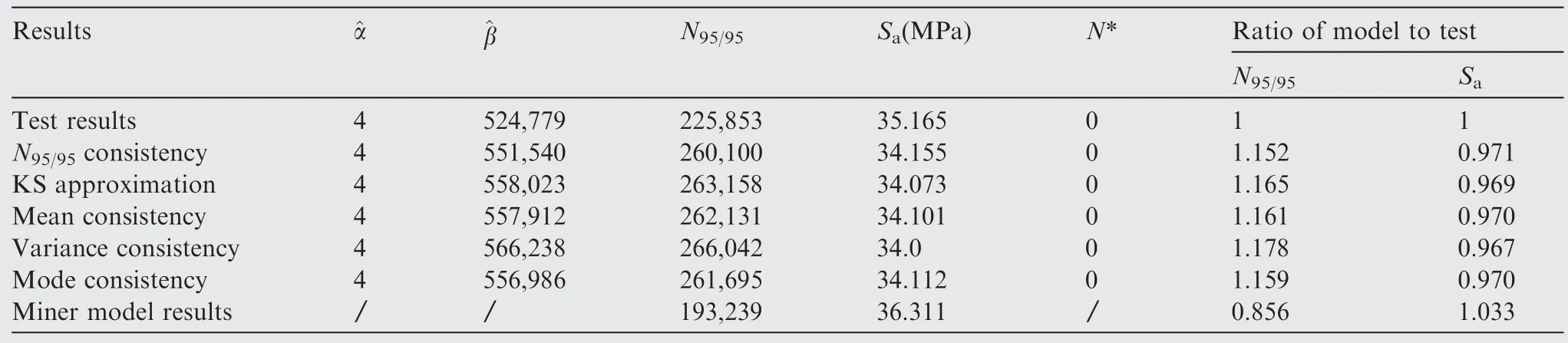
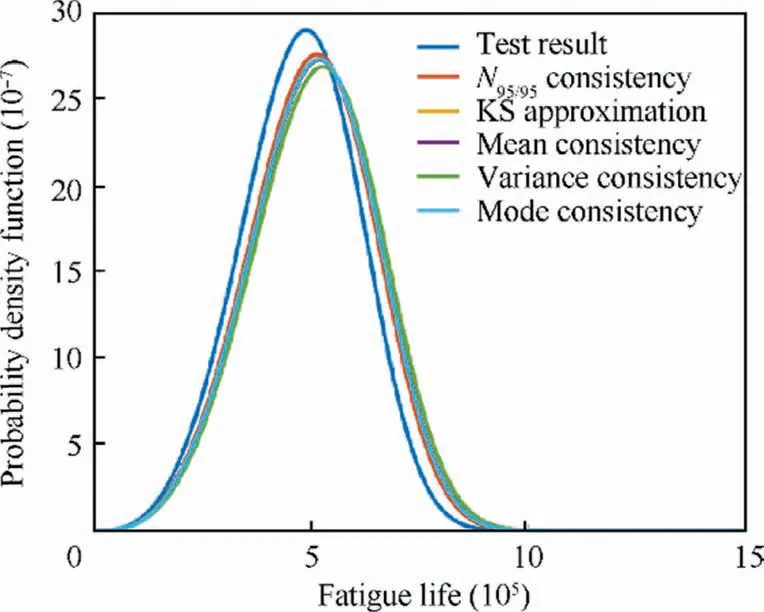
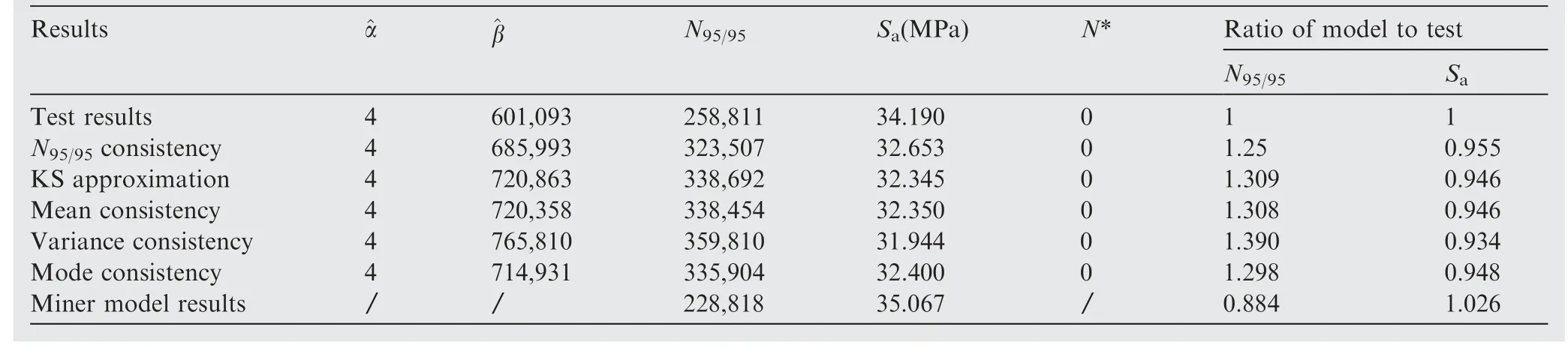
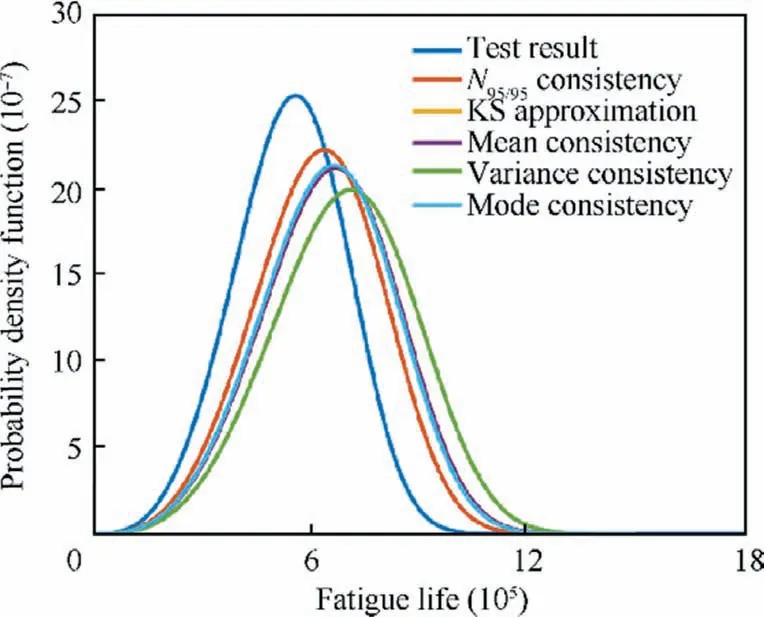
Smirnov test38can be used to check whether two samples come from the same population distribution by means of the empirical distribution function of samples.To set(X1,X2,...,Xn1)is a sample from populationXwith a continuous distribution functionF(x),and(Y1,Y2,...,Yn2)is a sample from populationYwith a continuous distribution functionG(x).It is assumed that the two samples are independent of each other.The hypothesis isH0:F(x)=G(x);H1:F(x)≠G(x),-∞ The exact distribution of above statistics does not depend on true distribution function of the population.For a given significant level α,letn=n1∙n2/(n1+n2),λ1-αcan be obtained from the relevant table,so thatWhen α=0.05,it can obtain that λ1-α=1.36.IfDn1,n2>Dn,α,then reject the null hypothesisH0.IfDn1,n2≤Dn,α,then accept. Fig.1 Flow chart of seeking cycle numberby dichotomy. For large sample data (X1,X2,...,Xn1) and (Y1,Y2,...,Yn2),the common methods are as follows:first,sort sample data.Next,divide it into an interval of appropriate size;Then calculate frequency of sampleXandYfalling into all interval ranges respectively.Finally,add them one by one to obtain the empirical distribution function of all interval. 2.2.1.Method of simplification to constant amplitude spectrum The simplification method for multi-level load spectra according to equivalent fatigue life is studied by taking fatigue life obeying Weibull distribution as an example.The steps to simplify multi-level load spectra to a constant amplitude spectrum are as follows: Step1.It is assumed that fatigue test data of aluminum alloy structure under multi-level load follows the Weibull distribution with shape parameter α of 4.Bayesian Jeffery method39is used to estimate scale parameter β and double 95%lifeN95/95,which is then substituted into thep-S-Ncurve to obtain stress amplitudeSaof constant amplitude spectrum corresponding to life distribution of multi-level load spectra. Step2.Firstly,the probabilistic statistical model of multilevel load spectra23is used to do numerical simulation of fatigue test data of aluminum alloy subjected to multi-level load,and fatigue life of large sample size is obtained.Secondly,the life distribution of model is estimated by the maximum likelihood method,and the shape parameter obtained is close to but not equal to 4.Then,according to one of the five criteria described below,it is appropriately transformed into the life distribution with shape parameter of 4,and the transformed distribution is taken as the life distribution under a certain constant amplitude load.Finally,the transformed life parameters are substituted intop-S-Ncurve to solve stress amplitude of constant amplitude spectrum. According to some criterion,the life distribution of model for multi-level load spectra is approximately transformed into a Weibull distribution with shape parameter of 4,that is,life distribution under a certain constant amplitude load on thep-S-Ncurve is obtained,and then stress of constant amplitude spectrum with the same effect can be gained.Due to shape parameter α in two-parameter Weibull distribution has been determined,the result of approximate transformation is only reflected in variation of scale parameter β.Therefore,the following five approximate criteria are proposed to transform life distribution of model into Weibull distribution with shape parameter α of 4. 1) N95/95consistency criterion The double 95% life consistency criterion means that the life distribution obtained by probabilistic statistical model is consistent with the double 95%lifeN95/95of Weibull distribution with shape parameter of 4.The fatigue lifeNC/Rwith confidenceCand reliabilityRis defined by The transformation formula calculated by using double 95% fatigue lifeN95/95is shown in Eq.(3). in whichmis the number of samples.2000 groups of sampling tests were carried out in the model simulation of multi-level load spectra test data,somis set as 2000.The life distribution of statistical model has the subscript 1,and Weibull distribution with shape parameter 4 has the subscript 2. Given α1,α2(α2=4) and β1,β2is obtained.The corresponding stress of constant amplitude spectrum is calculated by substituting β2intoS-β curve shown in Eq.(4) below.TheN95/95consistency criterion indicates thatN95/95formed by the constant amplitude spectrum after transformation is consistent with that of multi-level load spectra. whereA1andB1are constant. 2) The best Kolmogorov–Smirnov (KS) probability distribution approximation criterion The approximation criterion is to search for a scale parameter β in Weibull distribution with shape parameter of 4,so as to minimize the KS goodness of fit test statistics of life distribution obtained by probabilistic statistical model.The statistics of KS is expressed as Eq.(5). Parameters β2is obtained by MATLAB programming.Then substitute it intoS-β curve shown in Eq.(4) to calculate the corresponding constant amplitude fatigue load. 3) Mean consistency criterion The criterion is to make the mean of life distribution obtained by statistical model equal to that of Weibull distribution with a shape parameter of 4.The mean is defined as Eq.(6). 4) Variance consistency criterion The criterion is to make the variance of life distribution obtained by probabilistic model equal to that of Weibull distribution with a shape parameter of 4.The variance is expressed by Eq.(8) Thus,the transformation equation is shown in Eq.(9).α1,α2and β1are known,β2is obtained. 5) Mode consistency criterion Mode refers to fatigue life corresponding to the maximum value on the probability density function.The criterion is to make the mode of life distribution obtained by statistical model equal to that of Weibull distribution with shape parameter of 4.The modeMis obtained from Eq.(10) Similarly,it is obtained transformation equation shown in Eq.(11).Given α1,α2and β1,parameter β2is obtained.Then the fatigue life of constant amplitude spectrum is calculated byS-β curve shown in Eq.(4). Step3.The stress amplitude of the constant amplitude spectrum obtained from the life distribution of model in step 2 is compared with that of test data in step 1.The closer the two values are,the better the prediction of the proposed method which simplifies multi-level load spectra to constant amplitude spectrum based on the statistically consistent fatigue damage model. 2.2.2.Method of simplification to constant amplitude spectrum with arbitrary stress ratio The proposed simplification method in Section 2.2.1 only simplifies with same stress ratio,and it is further simplified and calculated.Firstly,the life distribution of multi-level load spectra model is simplified to the constant amplitude spectrum under the same stress ratio by using the method described in the previous section,and then it is converted to the constant amplitude spectrum with arbitrary stress ratio by using constant life diagram.The detailed method is as follows: Goodman linear model40is selected as the constant life curve,and all of them intersected with the horizontal axis at the same point σ0,where σ0represents ultimate strength of structural materials,as shown in Fig.3.Assuming that stress(Sm0,Sa0) under stress ratioR0is known,the stress (Sm,Sa)under arbitrary stress ratioRwith equivalent life rule be solved.Here,the arbitrary stress ratioRis suitable for fatigue test,and commonly used stress ratio isR=0.06 or-1. According to the properties of similar triangles,Eq.(12) is obtained in whichSmis mean stress,Sais stress amplitude. Smaxis the maximum stress andSminis the minimum stress,the stress ratio of fatigue is defined by Combining Eq.(12) and Eq.(13) yields the following expression: Fig.2 Goodman linear constant life diagram. In particular,R0=-1,that is,the given load is a symmetric load.The above equation is simplified to Eq.(15).Thus,givenR0andSa0as well asR,Sais obtained. 3.1.1.Simplify five levels spectra The low–high-low arrangement of five-level spectrum test data of the straight lugs from Ref.41was used to verify the method of simplifying multi-level load spectra to fewer-level load spectra.The calculation is as follows. The cycles-life rationi/Eiof each load level in five-level load spectra was calculated,and the results are shown in Table 1.Obviously,the ratio of cycles-life in level 1 is much smaller than that of the other four levels,so level 1 is directly cut off and the damage caused by it is without considering.That is,the original five levels spectrum becomes four levels spectrum. In accordance with the simplification method in Section 2.1,the four-level load spectra which has omitted level 1 was attempted to be simplified to three-level load spectra.The damage of level 5 in falling section was converted to level 3,which satisfiesThe numerical test using dichotomy method shown that distribution parameter of damagecaused by level 3 after conversion is approximately equal to that ofD5+D3whenpasses Smirnov test with the same distribution asD5+D3.The results are shown in Table 2. Krefers to the ratio of two statistical parameters ofandD5+D3in Table 2.It is seen thatKis very close to 1,indicating that the conversion method satisfies the equivalent damage in statistically significant.Thus,the original five-level spectrum is simplified to three-level spectrum shown in Table 3. In order to further test whether the distribution of damageDBof one loading block before and after simplification is equal,numerical sampling was conducted on damage calculation model of block spectrum again,and the results are shown in Table 4.It is obtained that the mean of damage before andafter simplification is equal,and the error of standard deviation is 1.05%. Table 1 Five-level spectrum test of straight lugs. When fatigue failure occurs,the number of spectral blocks isnB,which is calculated by Eq.(16): It is seen that when the damage of one block before and after the simplification is approximately equal,the distribution of number of spectral blocks should also be the same. The fatigue life test data of five-level load spectra for straight lugs are known,and the number of test spectrum blocks is obtained by dividing it by the number of cycles per spectral blocks,which is 3200.According to the probability correlation theory,ifN~W(α,β),thenN/n~W(α,β/n).Bayesian Jeffery method was used to fit parameter of number of experimental spectral blocks,and original five-level load spectra and simplified three-level load spectra were substituted into the probability calculation model ofnBrespectively for 2000 groups of numerical sampling.The estimated values of shape parametersscale parametermeanEand standard deviationare obtained as shown in Table 5.For comparison,Fig.3 shows the probability density curves of the three spectral blocks. As shown in Table 5 and Fig.3,the number of spectrum blocks in original five-level and simplified three-level load spectra are very close.The experimental results of the five-level load spectra show that the multi-level load spectra simplification method is feasible by first cutting off the lowest load of level 1 and then converting the damage of level 5 to level 3 by using equivalent damage rule.The damage of one loading block before and after simplification is statistical equal. Fig.3 Comparison of spectrum blocks number between experimental and model before and after simplification. 3.1.2.Simplify seven levels spectra To further verify feasibility of multi-level load spectra simplification method,seven-level load spectra was assumed,and given stress of load and cycle number are shown in Table 6.In order to use existingp-S-Ncurve of straight lugs,stress ratioRof the spectrum is set to 0.06.The stress amplitudeSawas substituted intop-S-Ncurve fitting based on test data of constant amplitude spectrum.The corresponding life distribution parameters of each load level was obtained for numerical calculation by substituting into damage statistical model of multi-level load spectra.As seen fromni/Eiin Table 6,cycle-life ratio of each load level is of the same order of magnitude,which does not differ greatly. Table 2 Statistical results of D5+D3= Table 2 Statistical results of D5+D3= Table 3 Simplified third-level spectrum Table 4 Comparison of damage in one loading block before and after simplification According to the simplification method,seven-level load spectra is simplified to six-level and five-level load spectra respectively.The realization method of six-level load spectra is to convert damage from level 7 to level 4,which satisfies the requirement ofThe numerical calculation using dichotomy found that distribution parameters of damage caused by level 4 is approximately equal toD7+D4whenpassed Smirnov test with the same distribution asD7+D4。The results are shown in Table 7.The comparison results of damage for one loading block before and after simplification are shown in Table 8.The mean of original seven-level load spectra is the same as that of the simplified sixlevel load spectra,and the ratioKof standard deviation is close to 1,indicating that the damage distribution before and after simplification is basically the same. The realization method of five-level load spectra is to convert the damage of level 7 and level 6 with lower stress into level 4 with the highest stress,satisfying the requirement ofBy using dichotomy,it is found that whenthe damage distribution parameter caused by the simplified level 4 is approximately equal toD7+D6+D4,andpasses the Smirnov test with the same distribution asD7+D6+D4,the results are shown in Table 9.The comparison of damage in one loading block before and after simplification in Table 10.The ratioKof the original seven-level load spectra and simplified five-level load spectra for meanEandstandard deviationis close to 1,and damage distribution of the two is basically the same. Table 5 Comparison of parameters estimated values Table 6 Assumed seven-level load spectra Table 7 Statistical results of D7+D4= Table 7 Statistical results of D7+D4= Table 8 Comparison of one loading block before and after simplification Table 9 Statistical results of D7+D6+D4= Table 9 Statistical results of D7+D6+D4= Table 10 Damage comparison of one loading block before and after simplification Numerical verification of the simplified seven-level load spectra shows that the proposed method is feasible to simplify seven-level load spectra to six-level or five-level.It achieves that damage of one spectrum before and after simplification is equal in a statistical sense. In the method of simplifying multi-level load spectra to fewerlevel load spectra proposed in Section 2.1,only the load levels in falling section were converted to the load level of highest stress,but the load levels in rising section were not simplified.The reason is that the load damage in rising section is not affected by load hysteresis effect,and the damage calculation model satisfies statistical consistency.The low stress load in rising section cannot be converted into a certain high load with equivalent damage rule. It has been verified in23that the probability calculation model of fatigue damage and life for constant amplitude spectrum,as shown in Eq.(17),is consistent,that is,theNfobtained by the model and the original fatigue lifeNobey same distribution. Damage caused by constant amplitude spectrum with cycle number ofnis calculated byD=n/N,whereNis the random fatigue life.μ is the mean of fatigue life.Due to the load in rising section is not affected by the load hysteresis effect,the corresponding damage is calculated byDi=ni/Ni.The damage of stress amplitudeS1in falling section andS2are respectivelyrepresented byD1andD2,then according to the equal damage criterion ofD1is converted toD2to satisfy Eq.(18). wheren1,n2andN1,N2are the number of cycles and fatigue life ofS1andS2,respectively.represents cycle number of stressS2after equivalent damage conversion. As showed below,based on two different fatigue life distribution models,it is proved that an appropriatewas not found to satisfy Eq.(18) under givenn1,n2andN1,N2. 3.2.1.Weibull distribution It is assumed that fatigue lifeNof material follows twoparameter Weibull distribution,i.e.,n~W(α,β),where shape parameter α is given.Then the probability density functionf(N) of fatigue life is defined by According to the chain rule of function derivative,fatigue damageDobeys the inverse Weibull distribution,that is,D=1/N~IW(α,β).The probability density functiong(D)ofDis expressed as Eq.(20). In addition,from Eq.(21)and Eq.(22),the mean and variance ofn/Nare given by Therefore,it is concluded thatn/N~IW(α,β/n).From the above proof can be obtainedn1/N1~IW(α,β1/n1) andn21/N2~IW(α,β2/n21). In order to prove invalidity of Eq.(18),a new cycle numbern21is introduced here,which satisfies the following equation: Son1/N1=n21/N2is true,that is,the damage distribution caused byS2with cycle numbern21is equal to that caused byS1with cycle numbern1. Then Eq.(18) becomes The fatigue lifeN2in the Miner linear criterion is taken as a certain value,and it is obvious that whenEq.(26) is true.Fatigue lifeN2obeys Weibull distribution,if Eq.(26) is required to be true,it means that mean and variance of damage around the equals sign should be equal. Namely,Eq.(27)and Eq.(28)are changed into the following form: The above equation indicates that Eq.(18)is not true,that is to say,it is proved that it is impossible to convert the low stress load levels in rising section to a certain high stress load level. 3.2.2.Lognormal distribution It is assumed that fatigue life follows Lognormal distribution,i.e.,N~lgN(μ,σ2),where standard deviation of logarithmic life σ is given.Then the probability density functionf(N) of fatigue life is defined by When Eq.(42)is true,it is obvious that Eq.(43)cannot be satisfied.It is proved that when fatigue lifeNfollows Lognormal distribution,low stress load levels in rising section cannot be converted to a certain load level of high stress by using equivalent damage rule. The feasibility of the proposed method of simplifying multilevel load spectra to constant amplitude spectrum was verified by using two kinds experimental data of three-level spectrum of straight lugs from Ref.23.Table 11 shows cycles numberniand fatigue lifeNunder same stress amplitudesSaifor threelevel load spectrum 1 (3-level1)and three-level load spectrum 2 (3-level2). The material of specimen cited in this paper is aluminum alloy,and fatigue life follows Weibull distribution and shape parameter α is generally set as 4.According to five equivalent criteria mentioned in Section 2.2,the model life distributions of two groups three-level spectra were transformed respectively.Table 12 shows transformed scale parameters β,the double 95% fatigue lifeN95/95,the number ofN* that the test data did not fall into transformed 95%life interval,and stress amplitudeSa.simplified constant amplitude spectrum.The test results in the table is constant amplitude stress obtained by substituting estimated scale parameter ^β intoS-β curve after obtaining fatigue life of multi-level load spectra by statistical method.In addition,N95/95andSawith stress ratioR=0.06 were compared with the corresponding test results. It is concluded from Table 12 that the maximum difference of ^β between test and value transformed by the five criteria is 7.90%.The number of test data that do not fall into 95% life interval is 0,and the ratios of model and test forN95/95andSais close to 1.Because Miner model did not consider load sequence effects of low stress loads on low loads,the ratio error ofN95/95between model and test was relatively large,indicating the effectiveness of simplification methods for multi-level load spectra in this paper.In addition,it is worth noting that stress amplitudeSaof simplified method in this paper is smaller than the corresponding test value,so the results are more conservative and meet requirements of engineering application. Table 11 Fatigue test data of three-level load spectra Table 12 Comparison of transformation results of life distribution for 3-level1 In Fig.4,the distribution of life obtained by approximate transformation of statistical model for three-level load spectrum 1 and that of test were compared.It is seen that life distribution of model obtained by using five approximateconsistency criteria has a small difference.Some are close to the test life distribution,and some are slightly away from it. Fig.4 Comparison of life distribution for 3-level1 between model and test. The above results are based on three-level load spectra 1 with stress ratioRof 0.06,which is further simplified to a symmetrical constant amplitude load with stress ratioRof-1.It is known in Ref.42that the ultimate strength of aluminum alloy 2024-T3 is 483 MPa.Table 12 shows that three-level load spectra 1 has been simplified to the stress amplitudeSa0of constant amplitude spectrumR=0.06,which is 34.155 MPa.According to the method simplified as constant amplitude spectrum with arbitrary stress ratio,Sa0is substituted into Eq.(14),and stress amplitudeSacorresponding to stress ratioR=-1 is 37.115 MPa. Similarly,the results of three-level load spectra 2 simplified to constant amplitude spectrum with stress ratioR=0.06 are shown in Table 13.It is seen that number of test data that do not fall into the 95% life interval is 0,and the ratio ofN95/95and stress amplitude between the model and the test is close to 1.The ratio ofN95/95between Miner model and test is small.Fig.5 shows comparison between life distribution of approximate transformation of the statistical model for three-level load spectrum 2 and test data,and the same conclusion is achieved as that of three-level load spectrum 1. Table 13 Comparison of transformation results of life distribution for 3-level2 Fig.5 Comparison of life distribution for 3-level2 between model and test. The transformation results of the five approximate criteria have little difference,and is selected according to actual situation.To sum up,in engineering application,a statistically consistent fatigue damage model was first used to conduct numerical simulation of multi-level load spectra fatigue test.Secondly,life distribution of obtained model was transformed in terms of some approximate criterion.Then transformed life parameter was substituted intop-S-Ncurve.Finally,stress amplitude of constant amplitude spectrum was obtained,which is the same as that of multi-level load spectra in life distribution. On the basis of the fatigue damage model and its statistical characteristics,the feasible simplified methods of fatigue spectrum loading combined with the technical principles of test was established to achieve the goal of efficient test.When the original multi-level load spectra by using equivalent damage rule is simplified to load spectra with fewer levels,equivalent damage does not mean equal fatigue life.The difference of life distribution before and after conversion is a multiple,but the number of loading blocks in fatigue failure satisfies the same distribution.The original multi-level load spectra were simplified to constant amplitude spectrum through equivalent fatigue life rule. In summary,the main findings are as follows: 1) The experimental verifications of the five and seven levels load spectra showed that the simplified method is reasonable.The lowest stress load was first cut off,and then the damage of low-level load was converted to load with the highest stress level.The number of spectrum blocks of original multi-level load spectra is very close to that of the simplified spectrum.The damage distribution before and after simplification is basically the same.The ratioKof mean and standard deviation was close to 1,which passed the same-distribution Smirnov test. 2) For multi-level load spectra arranged in low–high-low sequence,the damage calculation model satisfy consistent because load level in rising section is not affected by load hysteresis effect.The low stress load in rising section cannot be converted into the highest stress load with equivalent damage. 3) The maximum difference of distribution life between constant amplitude spectrum by approximate criterion transformation and test data is 7.90%.The number of test data that do not fall into the 95% life interval after transformation is 0,and the ratio of model to test forN95/95and stress amplitude is close to 1.In addition to simplifying multi-level load spectra to constant amplitude spectrum with the same stress ratioR,it is further simplified to constant amplitude spectrum with arbitrary stress ratio by using constant life diagram. Declaration of Competing Interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.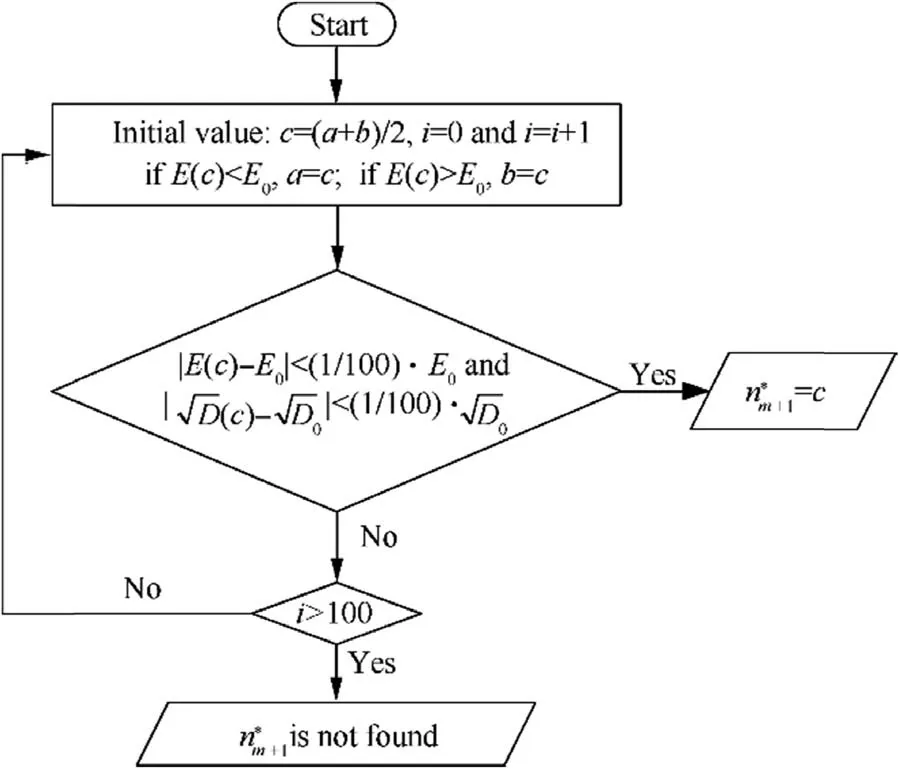
2.2.To simplify multi-level load spectra to constant amplitude spectrum













3.Results and discussion
3.1.Verification of simplification to fewer-level load spectra








3.2.A proof that some low stress load cannot be converted


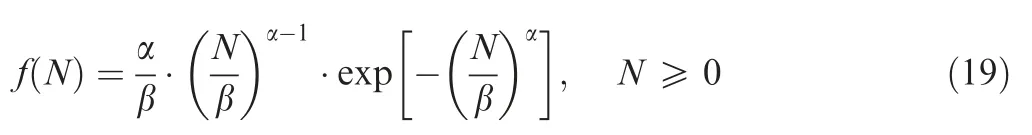
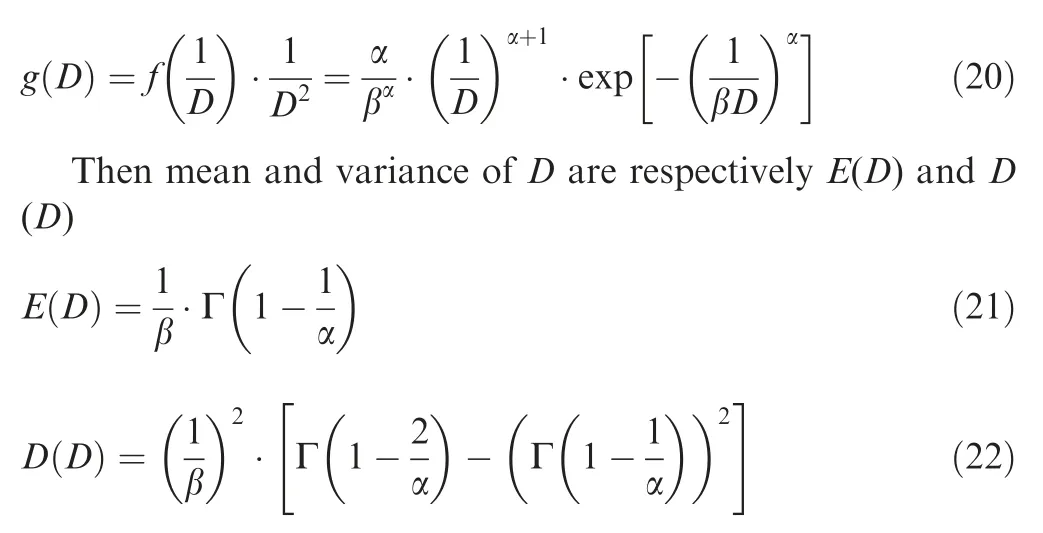
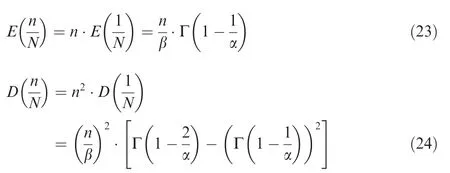




3.3.Verification of simplification to constant amplitude spectrum
4.Conclusions
 CHINESE JOURNAL OF AERONAUTICS2021年11期
CHINESE JOURNAL OF AERONAUTICS2021年11期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Parameter effects on high-speed UAV ground directional stability using bifurcation analysis
- Supersonic flutter control and optimization of metamaterial plate
- Review of in-space assembly technologies
- Utilisation of turboelectric distribution propulsion in commercial aviation:A review on NASA’s TeDP concept
- The influence of inlet swirl intensity and hot-streak on aerodynamics and thermal characteristics of a high pressure turbine vane
- Full blended blade and endwall design of a compressor cascade
