基于改进多入多出无模型自适应控制的二维直线电机迭代学习控制

曹荣敏 郑鑫鑫 侯忠生

（1.北京信息科技大学自动化学院 北京 100192 2.青岛大学自动化学院 青岛 266071）

0 引言

工业制造技术及自动化设备的高速、高精度特性已是未来制造业快速发展的趋势[1]，在二维直线电机系统中，XY轴由两台直线电机驱动，直线电机的运动轨迹相互垂直，直接产生直线推力，消除了电机与工作部件之间的驱动环节，具有响应快、定位准确、可靠性高等特点，广泛应用于制造业超精加工、微电子工程、生物工程、纳米技术领域[1-2]。然而，在二维直线电机系统中，各种不确定性，如时变参数、噪声干扰和强耦合非线性等都会影响系统的性能，降低控制精度[3-5]。文献[6-9]提出了基于双神经网络的前馈解耦控制、阶次优化、模糊控制和设计解耦控制器的控制方法，可以使二维直线电机系统获得较高的跟踪精度，但需要精确的二维直线电机系统的数学模型[10-12]。然而复杂系统的建模往往比较困难，在建模过程中因很难避免建模的误差而导致模型的不准确，因此，设计可靠且易于实现的不依赖精确数学模型的控制策略，可以有效解决二维直线电机系统运行中存在的问题[13]。

无模型自适应控制（Model Free Adaptive Control,MFAC）是一种数据驱动控制方法，控制律中可调参数具有不敏感性，而可调参数选取可以改变闭环系统的动态性能，因此无模型自适应控制具有更加平稳的过渡过程，能够很好地实现快速工业过程的控制[13-17]。迭代学习控制（Iterative Learning Control,ILC）在设计控制器时不需要事先已知受控系统的数学模型，可以实现对严格重复运作的系统在有限区间上的完全跟踪[18-19]。本文提出了一种改进多入多出-无模型自适应控制（Multiple Input and Multiple Output-MFAC,MIMO-MFAC）反馈控制和迭代学习前馈控制相结合的复合控制方案。一方面该方法可以摆脱对精确数学模型的依赖，充分利用二维电机在线输入输出数据实现稳定精密控制，与经典无模型自适应控制相比，可以进一步提高系统控制精度和抗干扰能力；另一方面可以使前馈和反馈优势互补，提高学习收敛速度和系统跟踪性能，进一步减小实时跟踪误差，提高控制精度，增强系统鲁棒性。最后通过实验对ILC复合控制方案进行了有效性验证。

1 二维直线电机模型辨识与验证

1.1 二维直线电机运动平台组成

本文所用二维直线电机运动平台是由两台运动轨迹相互垂直的永磁同步直线电机构成，整套运动平台装置主要由上位机控制软件、LINKS实时仿真机、计算机控制模块运动实验装置及二维直线电机平台构成，实验平台电气连接如图1所示。二维直线电机具体性能参数指标见表1。二维直线电机是郑州微纳公司生产的WMU系列U型直线电机，Links-RT是北京灵思创奇公司研发的通用半实物仿真平台。

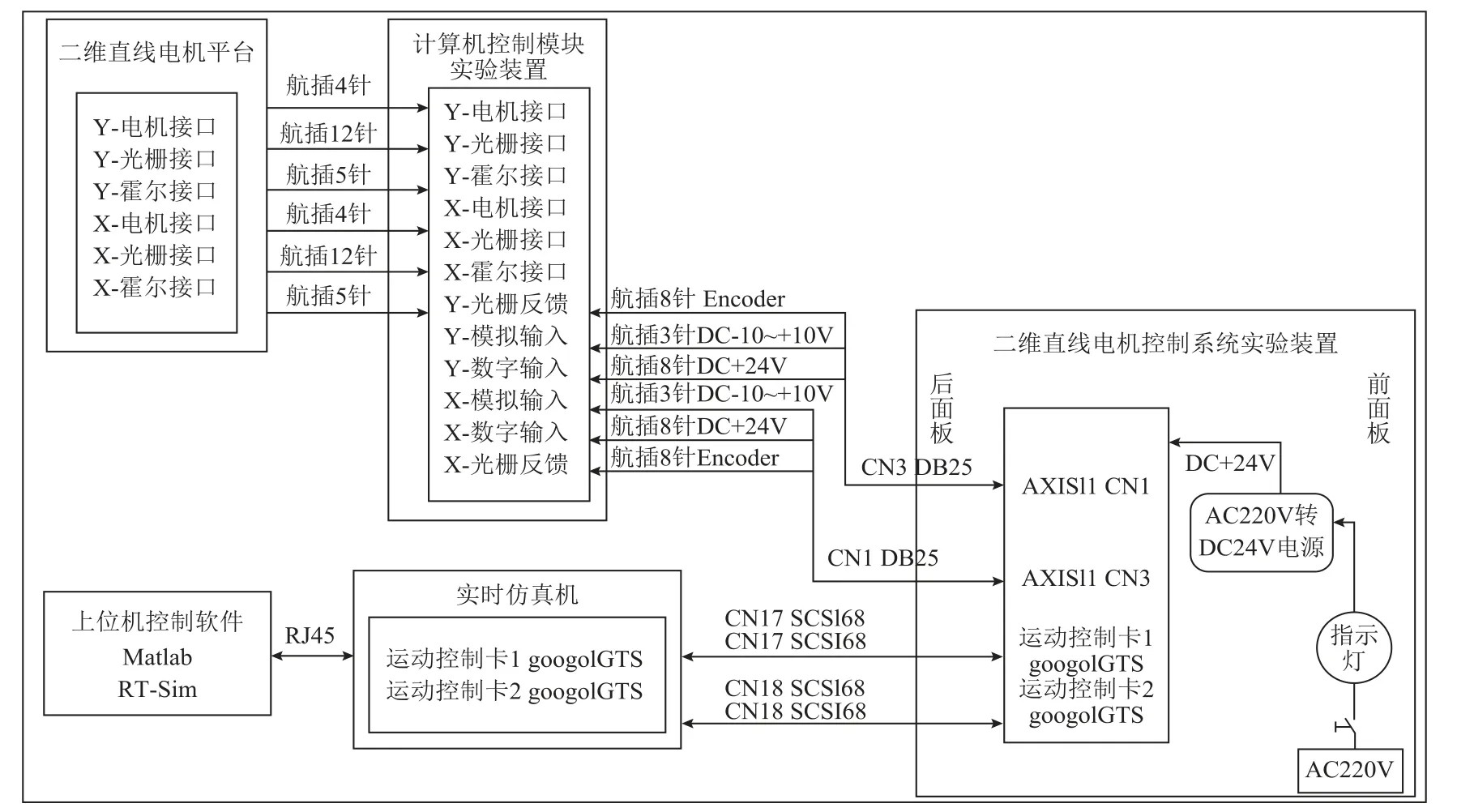
图1 二维直线电机运动平台电气连接图Fig.1 The electrical connection diagram of two-dimensional linear motor motion platform

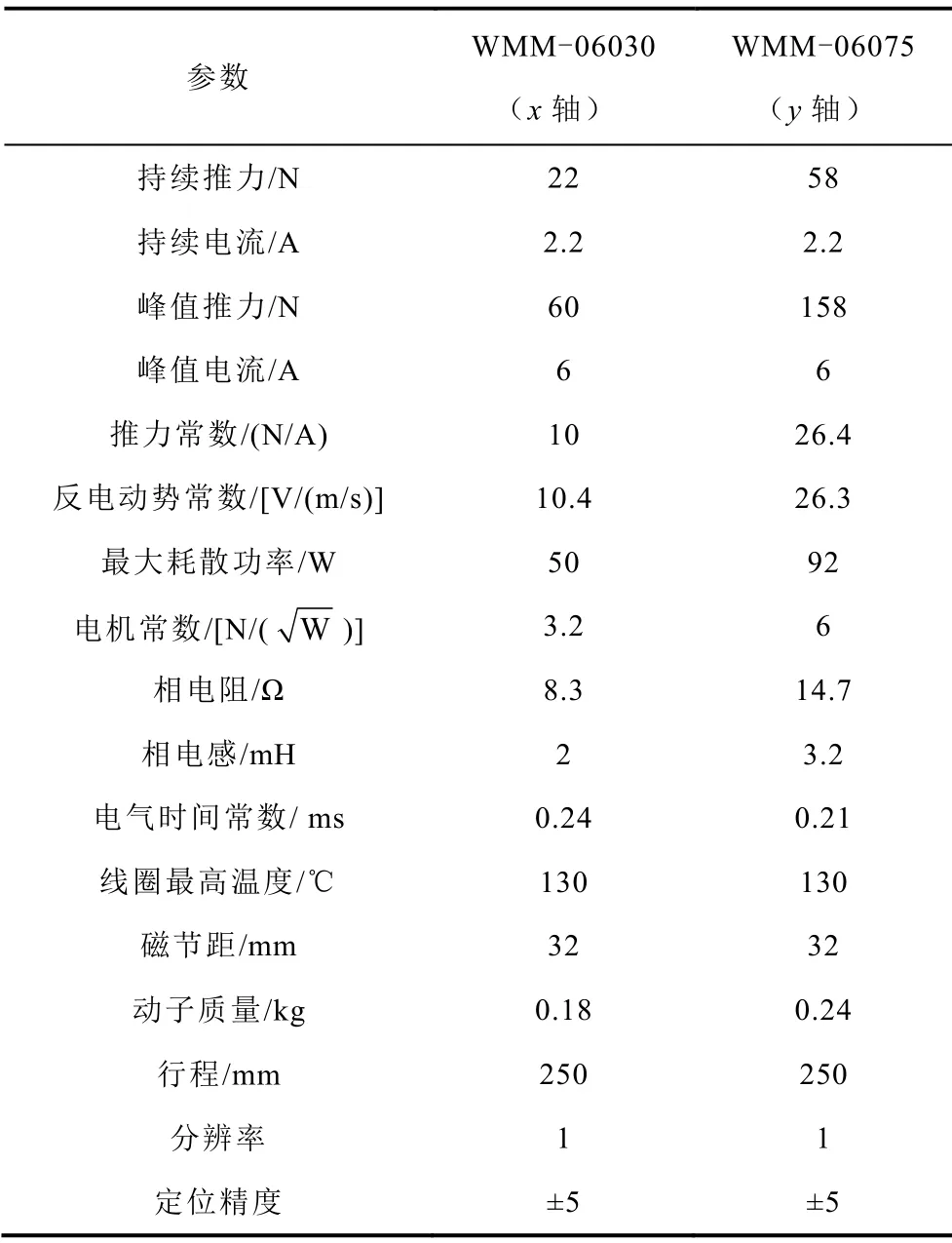
表1 直线电机性能参数Tab.1 performance parameters of linear motor

1.2 二维直线电机的简化模型及参数辨识

基于上述二维直线电机运动平台，在建立其动态数学模型时需要考虑诸多外部干扰和不确定性[20]，其中的主要因素是库仑摩擦力变化、端部效应和推动力脉动[21-22]。依据二维直线电机动力学特性，通过建模和简化[16]，二维直线电机状态空间模型为

式中，下标x、y分别为对应x、y轴分量；M为动子质量；x为直线电机位置；B为系统粘滞摩擦系数；Af为库仑摩擦力系数；为已知光滑连续函数，用来近似估计传统的库仑摩擦力；Ct为电磁推力系数；fe(x)用来近似估计传统的电磁推动力；D为其他误差和外部干扰；u为控制对象的输入力；K为控制器输入u的系数。

根据最小乘法原理，依据实验室设备，进行二维直线电机系统辨识，得到二维直线电机数学模型参数，见表2。将表2中参数代入式（1），两边同时除以K可得实际二维直线电机的数学模型。

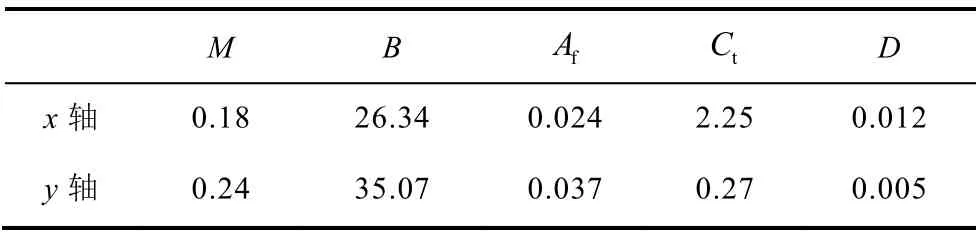
表2 二维直线电机辨识参数Tab.2 The identification parameters of two-axis linear

1.3 数学模型准确性实物验证

为确保1.2节建立的数学模型准确性，在Simulink上搭建此数学模型，在二维直线电机平台的Links-RT软件上建立等同可执行文件。在相同输入和相同配置情况下，分别采集数学模型输出结果与二维直线电机平台实物输出结果进行比较，并变换不同的输入信号，重复进行测试，直至数学模型与实际系统的输出误差在可接受范围内时（本文小于0.4mm），则可保证数学模型的准确性。

因为直线电机实际位置输出近似于正弦波[15]，所以实验设定输入位置信号x轴为4cos(2πt)，y轴为4sin(2πt)，t为采样时刻，采样频率为0.01s。图2所示为数学模型x轴和y轴的单轴输出误差。在运行的大部分时间内，误差在0.25mm以下，但起始时误差相对波动较大，是由直线电机x轴受y轴耦合作用引起，但依然保持在一定的范围内（0.4mm），通过实验证明了辨识出的数学模型的准确性。

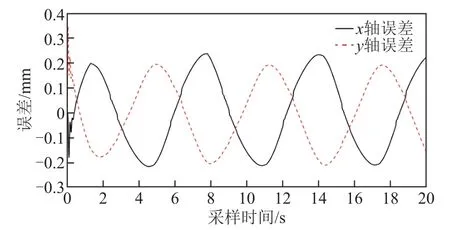
图2 数学模型单轴输出误差Fig.2 Single axis output error of simulation mathematical model

2 改进MIMO无模型自适应控制器设计

大多数实际的工业过程本质上都是MIMO的非线性系统。对于这类系统来说，由于系统的输入和输出变量之间存在耦合，其控制问题尤为复杂[13]。改进MIMO无模型自适应控制算法是针对二维直线电机位置控制过程中，输出产生了振荡和发散而提出的改进方法，是一种针对MIMO离散时间非线性系统的数据驱动控制方法。该算法控制器的设计仅需要系统输入输出数据，在一定的假设条件下可保障系统的闭环稳定性和收敛性。

2.1 基于紧格式线性化的改进MIMO-MFAC设计

一般MIMO非线性离散时间控制系统可表示为

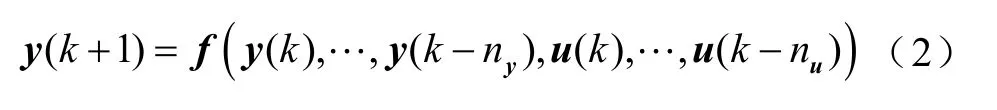
式中，k为采样时刻；u(k)、y(k)分别为k时刻的二维直线电机系统输入和输出；ny、nu为两个未知正整数，表示未知非线性向量函数。

假设2.1：f(…)关于u(k)存在连续的偏导数。

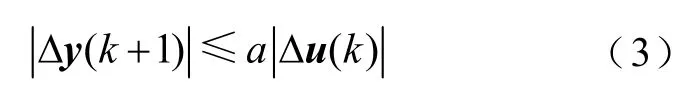
式中，a＞ 0 是一个常数；Δu(k)=u(k)−u(k−1)；Δy(k)=y(k)−y(k−1)。

当离散时间MIMO控制系统（式（2））满足假设2.1与假设2.2时，可以将式（2）转换为基于紧格式动态线性化的数据模型[13]。

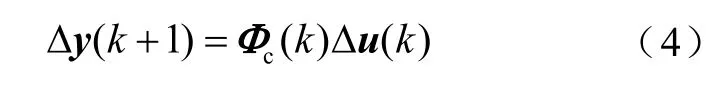
式中，Φc(k)为与采样时刻k相关的时变参数，Φc(k)∈Rm×m，称为控制域的伪雅可比矩阵（Pseudo Jacobin Matrix,PJM），且对于任意时刻k，Φc(k)是有界的。

为了严格稳定性实现，做如下假设。

假设2.3：系统的伪雅可比矩阵矩阵Φc(k)满足对角占优矩阵，即

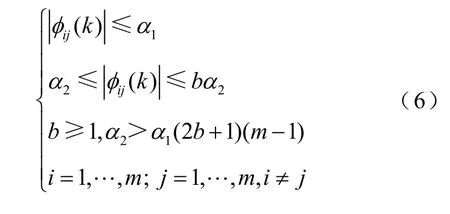
且Φc(k)中所有元素的符号对任何时刻k保持不变。

假设2.3是关于闭环数据输入输出关系的假设，对于多输入多输出非线性系统，由于对象模型未知，仅知道系统过去时刻的输入输出数据，系统输入输出数据关系的对角占优条件仅是描述系统各变量之间耦合的唯一可行选择。关于Φc(k)中元素符号的假设问题，对大多数自适应控制方法，比较合理的假设是控制增益为符号已知的常数。因为二维直线电机系统运行时，数据量是足够丰富的，假设2.3是可验证的。因此，这是一种合理的假设。

考虑控制输入准则函数

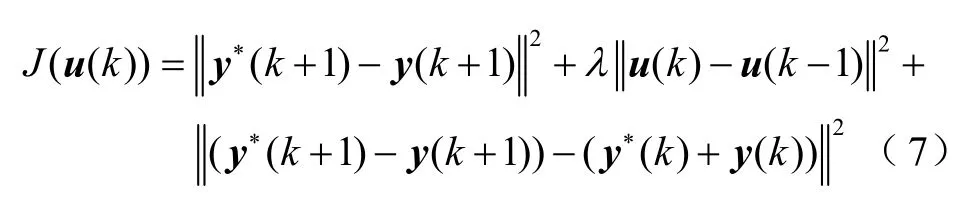
式中，权重系数λ＞0，用于限制二维直线电机控制输入量过大的变化；y∗(k+1)为电机系统k+1 时刻的期望输出。在准则函数式（7）中加入了第三项，用于对跟踪误差变化率即一阶差分的限制，以保证二维直线电机这种含有纯二阶积分环节的非自平衡系统在位置控制时的平稳和收敛。将式（4）代入到式（7）中，对u(k)求导并令其等于零。

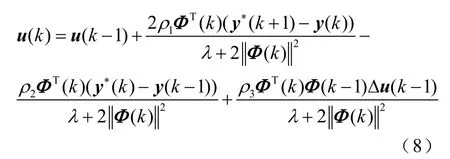
式中，ρ1、ρ2、ρ3为权重因子，用于限制相关各项过大的变化。ρ1和ρ2用于约束期望输出与实际输出之间的变化量，ρ3用于对控制量变化率的约束，对于二维直线电机系统，可以约束直线电机的输入不可瞬间有过大的变化，位置输出不可在突然间有过大的变化。伪雅可比矩阵的估计算法不变，利用改进MIMO系统的紧格式数据模型（4），给出参数估计准则函数为

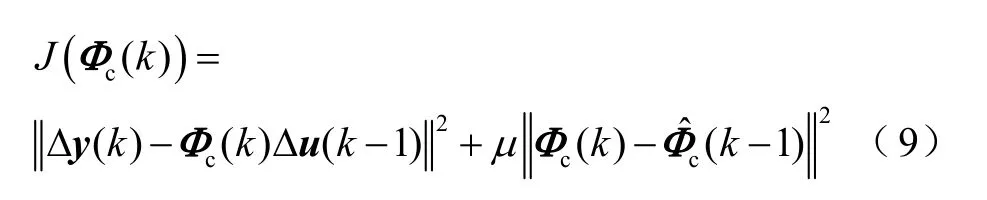
式中，权重因子μ＞0，用于限制伪雅可比矩阵估计值的变化率。基于二维直线电机系统的改进MIMOMFAC控制方案（式（8））、准则函数（式（9））极小化，可得估计算法为

式（10）是伪雅可比矩阵Φc(k)的估计值，其中，η是步长因子，η∈(0,2)，伪雅可比矩阵Φc(k)的估计值为

PJM重置算法为

至此，由控制算法（式（8）），估计算法（式（10）），重置算法（式（12））和（式（13））构成改进MIMO无模型自适应控制方法。

东阳市境内以丘陵与盆地为主，会稽山大盘山、仙霞岭延伸入境，形成三山夹两盆的独特地理环境。截至2017年底，东阳市拥有省级森林城镇5个，市森林覆盖率达到59.1%，林木覆盖率为60.0%，为省级森林城市。为了能够更好地了解东阳市森林古道的现状，挖掘森林古道的价值，发现森林古道存在的问题，笔者对东阳市境内的森林古道进行了调查研究与分析，希望能为森林古道的保护与修复提供参考。

2.2 改进MIMO-MFAC稳定性和收敛性分析

对于MIMO离散时间非线性系统，在满足假设2.1，假设2.2和假设2.3的条件下，改进MIMOMFAC控制方案具有如下性质：

当y*(k+1)=y∗是常数时，存在一个正数λmin＞0，使得当λ＞λmin时，闭环系统是有界输入有界输出（Bounded Input and Bounded Output,BIBO）稳定的，即输出序列{y(k)}和输入序列{u(k)}是有界的。

证明过程分三步：第一步证明伪雅可比矩阵估计值的有界性；第二步证明改进MIMO-MFAC系统跟踪误差收敛性以及系统有界输入有界输出（BIBO）稳定性；第三步证明期望输出y∗在非常值时稳定性和收敛性同样成立。具体如下：

1）本文改进MIMO-MFAC算法，并未涉及其中的伪雅可比矩阵的估计算法，故可保证PJM估计值的有界性[13]。

2）证明MFAC系统跟踪误差收敛性以及BIBO稳定性。

稳定性和收敛性分析中需要用到Gerschgorin（盖尔）圆盘原理。令A=(aij)∈Cn×n，定义Gerschgorin圆盘为

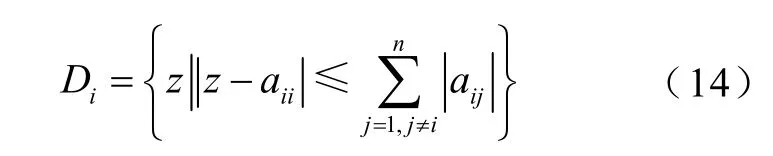
其中，z∈C,1 ≤i≤n，则矩阵A的所有特征根z1,z2,…,zn都满足。

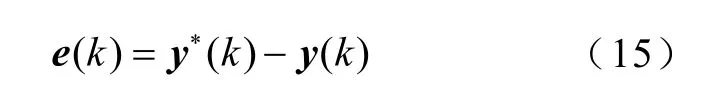
依据紧格式线性化模型（4）和控制律（8）可得

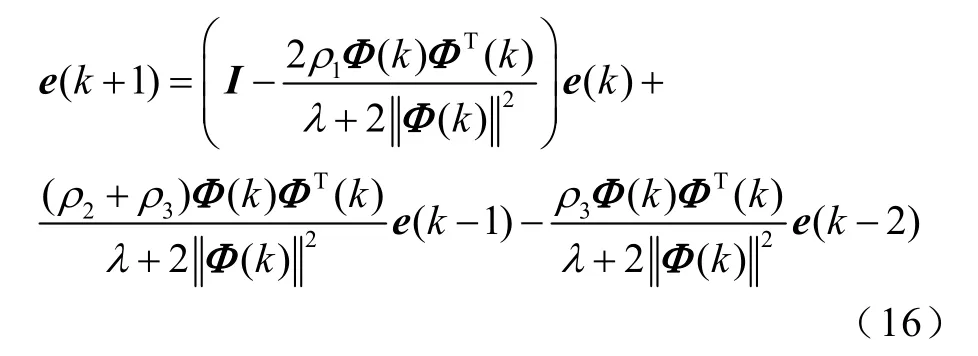
再根据圆盘定理，并利用三角不等式可得

同理，当ρ1,ρ2,ρ3⊂(0,1)是可调参数，存在正数d2和d3，谱半径不等式（20）可转换成不等式为

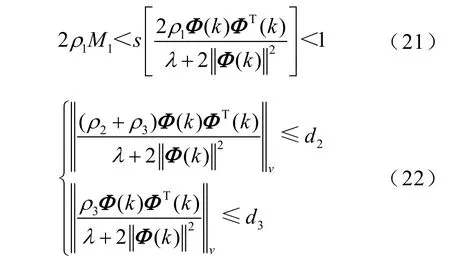
结合上述，在式（17）两边取范数得

至此，证明了输出误差序列有界且收敛。因为y*是给定常量，且e(k)有界，因此根据式（15）得出系统输出序列{y(k)}的有界性。

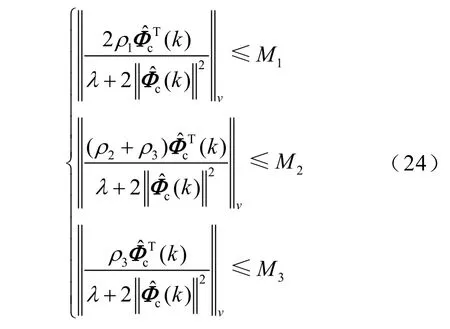
结合改进MIMO-MFAC控制律（8）和式（24）合并得

式（25）证明系统输入序列{u(k)}是有界的。

3）建立增广系统。

上述过程证明了在期望输出信号恒值条件下，改进MIMO-MFAC控制算法针对复杂非线性系统时的稳定性和单调收敛性。但实际应用过程中，系统期望输出大多是时变信号，为了佐证在此条件下稳定性和收敛性依然成立，可建立增广系统[17]，按照类似步骤2）的方法进行严格理论证明。

3 改进MIMO-MFAC方法的实验验证

当二维电机运行过程中，通过二维直线电机配有的光栅编码器（位置传感器）测量实际位置输出，反馈给控制器，与期望位置轨迹比较，如果有误差，则通过控制器中的改进MIMO-MFAC控制律进行修正，重新产生新的控制输出。系统按照采样周期不断采集新的位置输出，周而复始进行此过程，目的就是不断修正位置误差，使输出很好地跟随输入的变化。运行过程中的数据均通过Links-RT数据采集平台采集、存储，通过编程用曲线显示出来。本文是对二维直线电机系统位置进行控制。在实物系统建立基于Links-RT半实物仿真控制程序，其中相应的DAC模块分别作为二维直线电机的xy轴驱动器输入，光栅编码器反馈输出作为二维直线电机的位置输出，将整个算法文件形成、编译、生成可识别代码，由专用软件RT sim读取并配置，下载到硬件在环DSP仿真器中，最后通过Elmo Studio驱动器，控制电机运动。

二维直线电机系统运行时x轴位置期望轨迹为0.14sin(2πt)，y轴位置期望轨迹为0.14 -0.14cos(2πt)，t为采样时刻，采样时间间隔为0.01s，参数λx=λy= 1.2，验证改进MIMO-MFAC方法实际运行位置跟踪特性，图3所示为xy轴实际位置和期望位置的运行曲线采集图。从图3可以看出x和y轴具有很好的运行特性，实际位置输出能够很好跟随期望位置输入的变化。

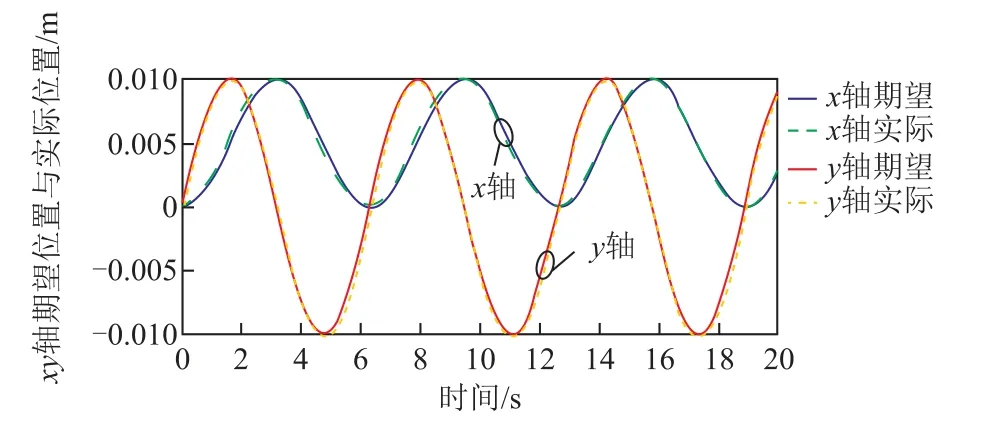
图3 xy轴实际运行位置数据采集图Fig.3 Data acquisition diagram of xy axis actual operation positions

4 基于改进MIMO-MFAC的迭代学习控制

此控制方案的收敛性分析采用在纵向学习控制收敛品质（周期运行的收敛速度的定量指标）中引入横向收敛品质（控制策略的跟踪误差以连续的采样点为基准的有限步收敛的定量指标）的概念。为了对非周期性扰动的收敛速度进行衡量，故将改进MIMO-MFAC反馈控制和迭代学习前馈控制相结合可达到更准确的同步运动和动态性能，使二维直线电机位置跟踪误差最小。

4.1 控制算法设计

由于二维直线电机运行时对扰动和系统参数变化较敏感，易受不确定摩擦力等影响，为进一步提高控制精度，在改进MIMO-MFAC控制器设计中加入迭代学习控制（ILC），形成复合控制方案。其基本思想是用迭代学习控制作为重复任务系统的经验补偿，目的是为了减少系统干扰影响和对象模型参数部分未知的补偿[23]。其中，改进MIMO-MFAC反馈控制器具有强鲁棒性，用以保证系统稳定，迭代学习前馈控制用来克服干扰，实现期望输出精度补偿，两者结合，使前馈和反馈优势互补。具体算法框图如图4所示。

图4中的复合迭代学习控制系统是二维直线电机在有限时间区间上重复执行相同控制任务的系统，也就是任务执行是在有限时间区间T上进行重复迭代的，在第k次迭代时，对于给定的期望输出轨迹yd(t)，控制输入uk(t)，位置跟踪误差ek(t)，系统的控制输入uk(t)是前馈输入和反馈输入的叠加，表示为

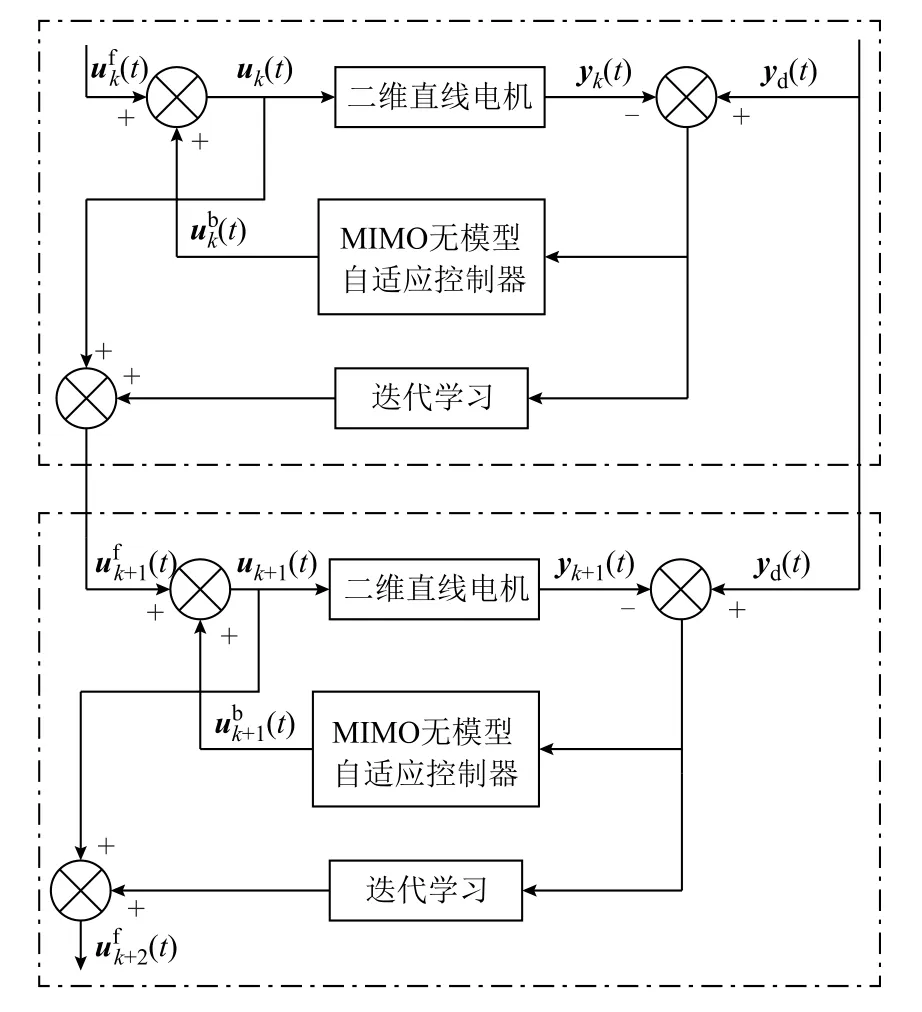
图4 复合迭代学习控制算法框图Fig.4 The compound scheme structure diagram

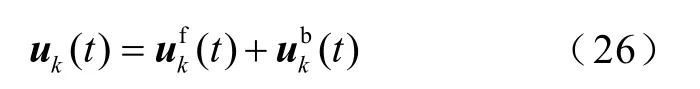
式中，L为定常学习算子。迭代学习控制需要储存前一次迭代过程的跟踪误差和控制输入数据，以便计算当前时刻下的迭代控制输入，本质上是依赖存储的控制方案。因此，选择离散时间迭代过程是合适的。在复合迭代学习控制器中，前馈控制器是PD型迭代学习前馈控制器，其算法为

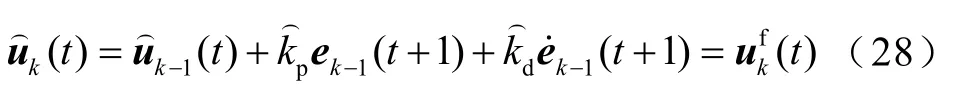
在实际应用中P型迭代学习律能快速降低误差，提高迭代效率，而D型迭代学习律则能减小超调，提高响应速度。k为迭代次数，为学习控制输入常数。反馈控制器是基于改进MIMO-MFAC无模型自适应控制，在文章第2节和第3节已经具体研究，在这里将其算法重新表示为

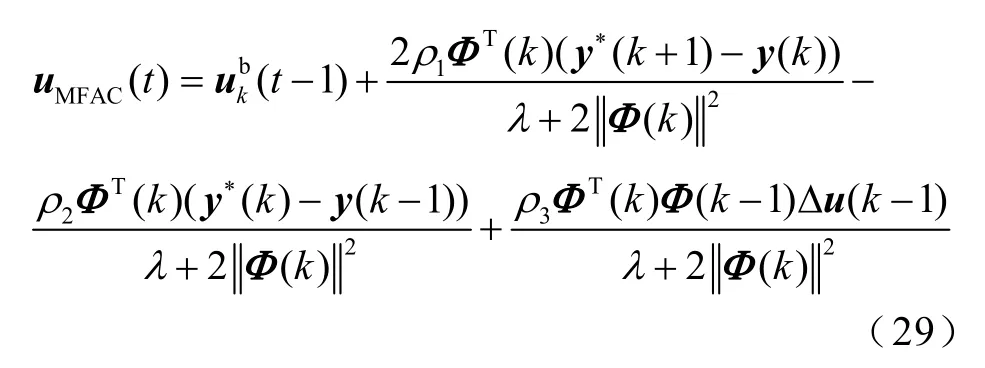
将式（27）和式（28）代入式（29）中，得到基于改进MIMO-MFAC的迭代学习控制算法为

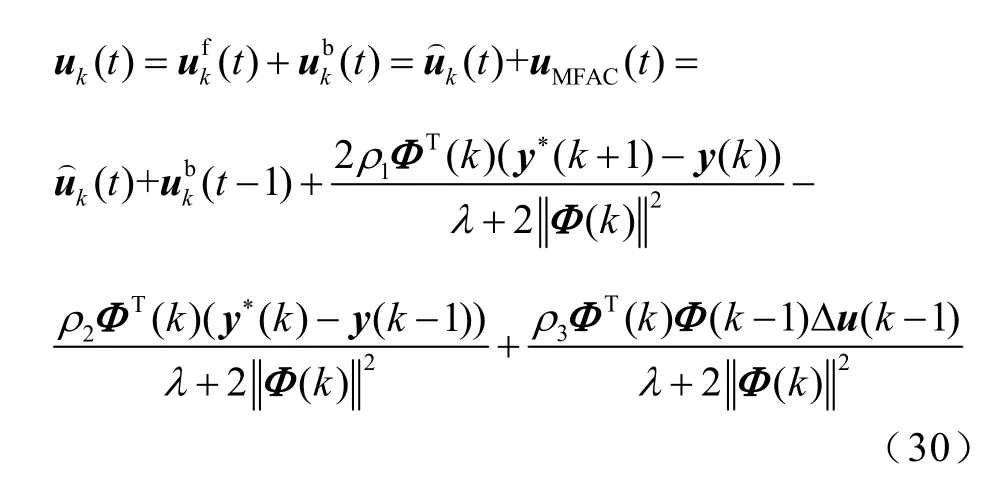
4.2 实验研究

在二维直线电机实验平台上验证基于改进MIMO-MFAC的迭代学习控制算法时，发现随着复合控制算法迭代次数的增加，单轴位置跟踪误差曲线虽然进一步减小，但在时间轴上，位置跟踪误差曲线出现振荡现象，并且振荡幅度有增大的趋势。这是由于二维直线电机伺服系统还存在电磁系数改变、机械温度变化、永磁体磁链波动等各种实际扰动因素，这些实际扰动因素具有不确定性，如果不消除或者抑制，则会沿迭代轴的反复学习逐渐积累，积累到一定程度会严重劣化迭代学习的收敛效果。

为了防止迭代产生的“锯齿”干扰信号破坏系统稳定性，故在系统结构中加入低通滤波器来过滤部分高频干扰信号，减缓“锯齿”振荡。本文二维直线电机复合迭代学习控制系统的任务执行是在有限时间区间T上进行重复迭代的，实验中，有限时间区间T为 20s，x轴位置期望输出轨迹为0.1sin(2πt)，y轴位置期望轨迹为0.1-0.1cos(2πt)，迭代控制前馈输入初始值，迭代学习控制律采用PD控制律，其中，改进MIMOMFAC反馈控制算法参数不变，实验结果如图5和图6所示。

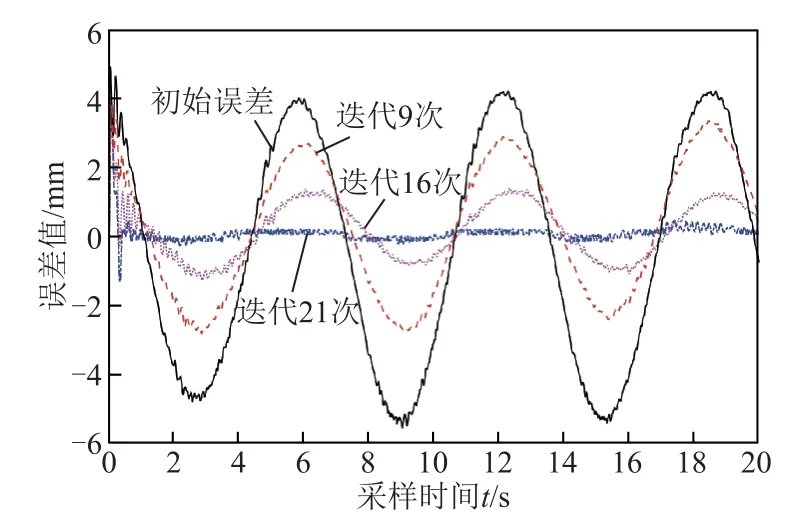
图5 x轴复合迭代学习控制位置误差比较图Fig.5 x-axis compound ILC position error comparison in experiment

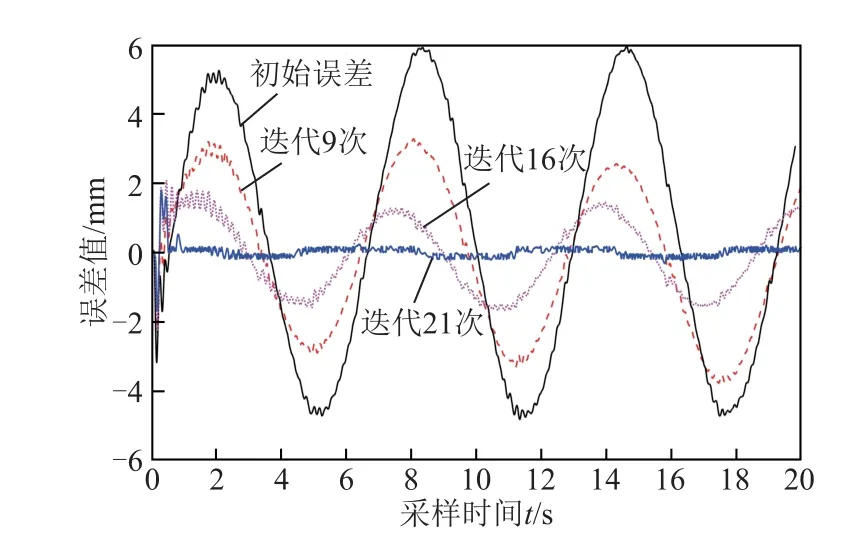
图6 y轴复合迭代学习控制位置误差比较图Fig.6 y-axis compound ILC position error comparison in experiment

实验结果表明，仅在改进MIMO-MFAC反馈控制器作用下，单轴跟踪位置误差比较大，误差曲线类似正弦波和余弦波，最大误差值在4mm左右。但加入迭代学习前馈控制器作用后，单轴位置跟踪误差会随着迭代次数的增加而减小，在迭代21次后，单轴位置跟踪误差趋于0，而迭代次数超过21次后，输出结果基本相同。由于实际实验中存在随机干扰和其他不确定性因素，导致改进MIMO-MFAC迭代学习控制下的单轴位置误差无法完全降低为0。

5 结论

本文提出了一种改进MIMO-MFAC的迭代学习（ILC）复合控制方案，在改进MIMO-MFAC反馈控制器基础上，加入迭代学习前馈控制器，形成复合ILC控制算法。改进的MIMO-MFAC反馈控制方案可以显著减小位置控制误差，克服控制过程中的振荡现象，优于没有改进的MIMO-MFAC算法，优于传统的用两个单轴控制器控制二维直线电机的XY轴等方法，并对其稳定性和收敛性进行分析和论证。迭代学习前馈控制用来克服干扰，实现期望输出精度补偿。二维直线电机控制实际实验表明，改进MIMO-MFAC反馈控制与ILC前馈控制优势互补，进一步减小位置误差，提高跟踪精度，从而进一步提高系统的整体控制性能。