基于差分进化算法的三维电场传感器解耦标定方法

吴桂芳 崔 勇 刘 宏 张 磊

（1.中国电力科学院有限公司 北京 100192 2.北京航空航天大学自动化科学与电气工程学院 北京 100191 3.国网山东省电力公司电力科学研究院 济南 250003）

0 引言

基于空间电场信息感知的三维电场传感器在电力、航空航天、气象和国防等诸多重要领域具有良好的应用前景[1-6]。近年来随着直流输电工程的投运，电力系统中的工程设计、电磁环境评价、带电作业、智能巡检等重要工作，都对三维空间电场的测量提出了迫切的需求。然而，到目前为止并没有成熟可靠的空间电场传感器及该类传感器的标定方法。

直流输电线路周边的电场由两部分组成，分别是极导线产生的标称电场（静电场）和导线电晕放电释放电荷产生的附加电场，这两部分电场共同形成了直流电场，因此输电线路周边的直流电场又常被称为直流合成电场。

根据电场传感器测量原理不同，现有直流电场传感器可分为旋转感应式、微机电系统（Micro-Electro-Mechanical System,MEMS）式和光学式。旋转感应式电场传感器可以测量直流合成电场[7-11]，也称为场磨式电场传感器；基于MEMS技术的电场传感器的工作原理与旋转感应式相似[1,7]，但是较多地适用于标称电场的测量中，光学电场传感器以基于晶体Pockels效应或电光Kerr效应为主。

传感器标定就是利用精度高一级的标准器具对传感器进行定度的过程，从而确立传感器输出量和输入量之间的对应关系，通过标定可获得三维电场传感器灵敏度系数等性能参数。因此空间三维电场传感器的标定/校准方法的研究具有重要意义[12]，而对三维直流合成电场传感器来说，标定是测量中一个非常重要的步骤，只有通过标定，才能在实际测量中获得准确的电场信息。

对于直流合成电场传感器的校准，目前主流的方法仍然是采用平行板电容结构产生标准的均匀静电场，并利用该静电场模拟直流合成电场[13-14]。其主要原因在于直流合成电场测量所使用的场磨式电场传感器在接地时可以有效地释放积累电荷，因此空间电荷产生的附加场和极导线本身产生的静电场二者的叠加场可以通过平行板电容结构进行统一模拟。对一维直流电场传感器进行标定，标准的均匀电场产生通常采用平行板式装置。其原理是利用两块足够大的平行金属极板构成一个电容器，然后在两平行极板之间施加电压，从而形成一个标准静电场。根据IEEE关于直流电场强度和离子相关量测量的标准[14]，可设计标定装置的平行极板尺寸和间距，确保电场传感器避开标定装置边缘，使得传感器所处电场的均匀性较好。对于三维电场传感器的标定，可以采用一维标定装置实现，即在一对平行极板间依次施加三个方向的电压，同时传感器需要在标定装置内配合支撑结构进行相应的旋转；或者采用三维标定装置实现，即在三对平行极板间同时或依次施加三个电压（此时三维传感器不需要进行空间旋转，标定过程均保持静止状态，仅需要支撑机构确保其处于标定装置的适当位置）。无论采用哪种标定方式，电场传感器维间耦合的准确解耦都是传感器标定的关键问题。

基于求逆矩阵运算的标定方法是当前国内外常用的三维电场传感器解耦标定方法[15-17]。自20世纪90年代以来，维间耦合解耦的方法并无太大的变化，仍是使用迭代寻优的办法，只是在约束条件、目标函数等方面进行了改进[15-20]。2007年，D.M.Mach和W.J.Koshak[19]两位学者提出了一种方法，不寻找灵敏度逆矩阵，因为该矩阵并不唯一，先求出灵敏度矩阵，使标定工作简化；同时还为每个场磨赋予一个权重系数，可以在得到的总电场中增强或减弱某一场磨带来的影响。例如，一旦传感器阵列（阵列由6～8个一维场磨构成，分布在飞机的不同位置处）中部分传感器异常，该传感器的权重值就会降低，从而减弱传感器异常带来的影响。除此以外，对于灵敏度矩阵的数值迭代方法，也曾有学者提出其他的解决办法。闻小龙等[2]于2014年提出的基于共面去耦结构的三维空间矩阵测量方法，将三个传感器共面不共线放置，保证了灵敏度矩阵的可逆，并对其求逆可以得到实际三维电场强度与传感器读数的关系。李冰等[20]于2017年提出使用遗传算法直接对灵敏度逆矩阵进行优化，该算法有很大概率可以找到全局最优解，还可以跳过矩阵求逆或伪逆，避免在这步骤中可能产生的误差，但标定体系不够完善。

本文在三维可调外界电场的情况下建立了同时含有维间耦合和角度偏差的标定模型，提出了在该模型下基于差分进化算法的求解灵敏度系数矩阵的方法，最终实现三维电场矢量传感器的标定。在三次测量为一组、每组5 000次迭代的设置下，找到灵敏度系数矩阵的较为接近（误差率＜3%）的解的概率极大。另外，在进行测量校准时，最好角度的范围满足α∈[180°,270°]，γ∈[270°,360°]，这样可以进一步提升算法的精确度。

1 三维电场解耦标定模型

1.1 传统方法存在的问题

对于三维电场传感器，其三个感应电极方向分别与笛卡尔坐标系中的X、Y、Z轴方向相对应。三个方向的测量电极可分别感应出电压信号Ux、Uy和Uz。理论上，三个方向的感应电压分别对应电场的三个分量。然而，由于传感器在设计过程中很难做到三个感应电极间完全去耦合，因此会导致在实际电场测量中，Ux、Uy和Uz中也会包括其他方向的电场分量，即某方向的测量电极感应电压不仅与本方向的电场有关，而且还与另外两个方向的电场有关。为了准确地得到某一方向上电场测量结果，须对测量结果进行还原，这个过程可称为电场传感器解耦。这种耦合关系可以表示为

式中，U为电场传感器三个测量电极的输出向量；λ为电场传感器的耦合灵敏度矩阵，该矩阵是电场传感器的固有属性；E′为被测电场向量。

将式（1）展开，可得

式中，λij为测量单元i对j方向电场的灵敏度系数，i=1,2,3，j取1，2和3分别对应X、Y、Z方向。

基于传统方法，对此三维电场传感器的标定过程为：将传感器放置于三维电场标定装置中，使得传感器的三个感应电极分别与标定装置的X、Y、Z方向重合，通过改变标定装置三个方向的电压实现标定电场值的变化，进而可以求出电场传感器的耦合灵敏度矩阵λ。然而，该方法需要在标定过程中确保感应电极与电场方向完全重合，该要求对于标定装置的设计和标定人员都提出了较高的要求。例如，需要增加额外的对准机构和其他传感器确保完全重合，将会增加校准装置设计的复杂度和工作人员的操作难度，不利于传感器标定结果的一致性和准确性。

本文针对该问题，提出一种新的三维电场传感器解耦标定方法，其基本思路为：通过建立含有维间耦合和角度偏差的标定模型，结合差分进化算法实现对灵敏度系数矩阵的求解。该方法将简化标定装置设计的复杂度，同时降低标定过程的难度。这种模型下，通过传感器粗略的空间角度信息以及标准电场的电场强度值，就可以根据传感器的输出电压值求解出灵敏度系数矩阵，使得同时考虑维间耦合和空间位置角度偏差成为可能，这是目前广泛采用的其他模型所不具备的。

1.2 标定模型坐标系建立

设XOYZ为自然坐标系，X′OY′Z′为传感器坐标系。对于确定传感器所在空间的位置，需要三个角度，用三个旋转角（α,β,γ）分三步表示。假设电场校准装置外安装多自由度旋转机构，再将该机构通过一非金属刚体（如木头、树脂等）与传感器夹持连接。由于刚体采用非金属材料，其本身不会畸变电场。由处于电场校准装置外部的旋转机构带动传感器发生三种旋转：刚体在垂直于平行板极板平面方向运动，带动传感器绕Z轴（旋转之前Z轴与Z′轴重合）旋转α角；刚体自转，带动传感器绕Y′轴旋转β角；刚体在垂直于纸面方向运动，带动传感器绕X′轴旋转γ角。

首先，记传感器绕Z轴逆时针转过的角度为α（顺着坐标轴正方向看去），得到第一个坐标系X1OY1Z1，如图1所示。

图1 传感器第1次旋转角度示意图Fig.1 Diagram of the first rotation angle of the sensor

该旋转变换的坐标系转换方程为

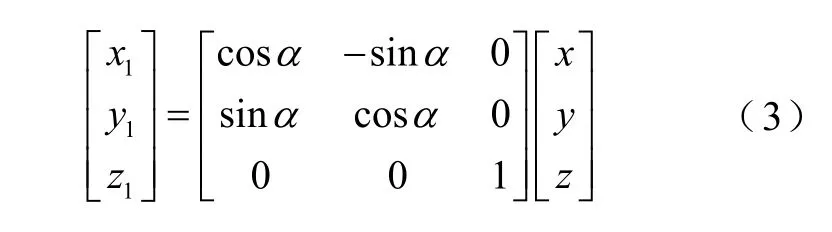
记式（3）右侧第一个矩阵为坐标系转换第一矩阵K1。

同理，记传感器绕Y1轴逆时针旋转的角度为β，得到新的坐标系X2OY2Z2，如图2所示。

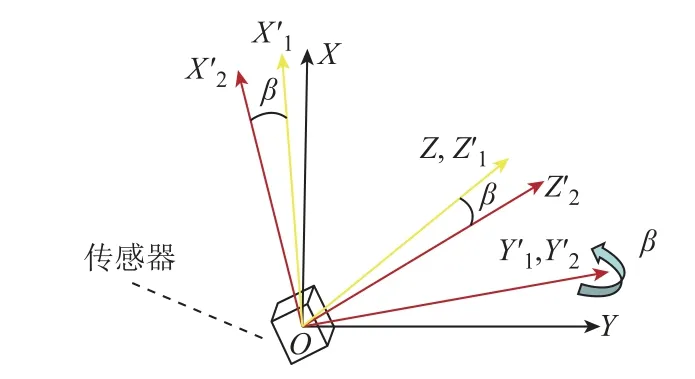
图2 传感器第2次旋转角度示意图Fig.2 Diagram of the second rotation angle of the sensor

可得到坐标系转换第二矩阵为

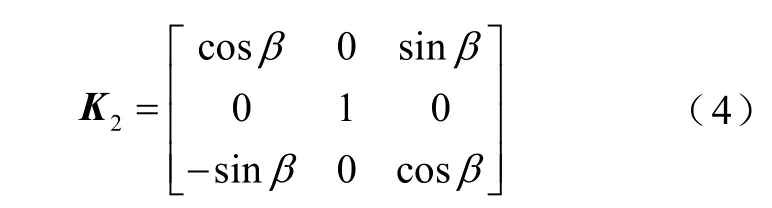
最后，绕X2轴逆时针旋转γ角度，得到新的坐标系X3OY3Z3，如图3和图4所示。

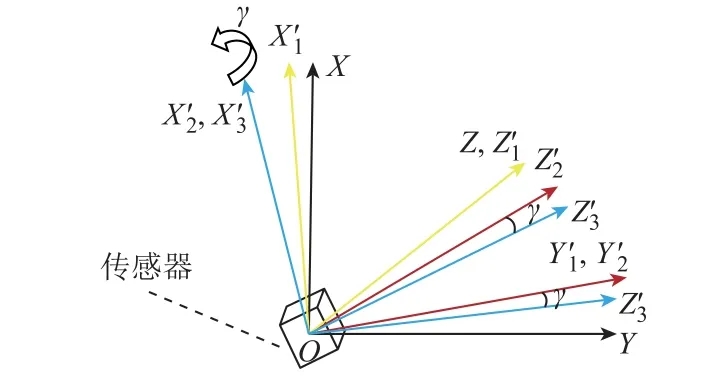
图3 传感器第3次旋转角度示意图Fig.3 Diagram of the third rotation angle of the sensor

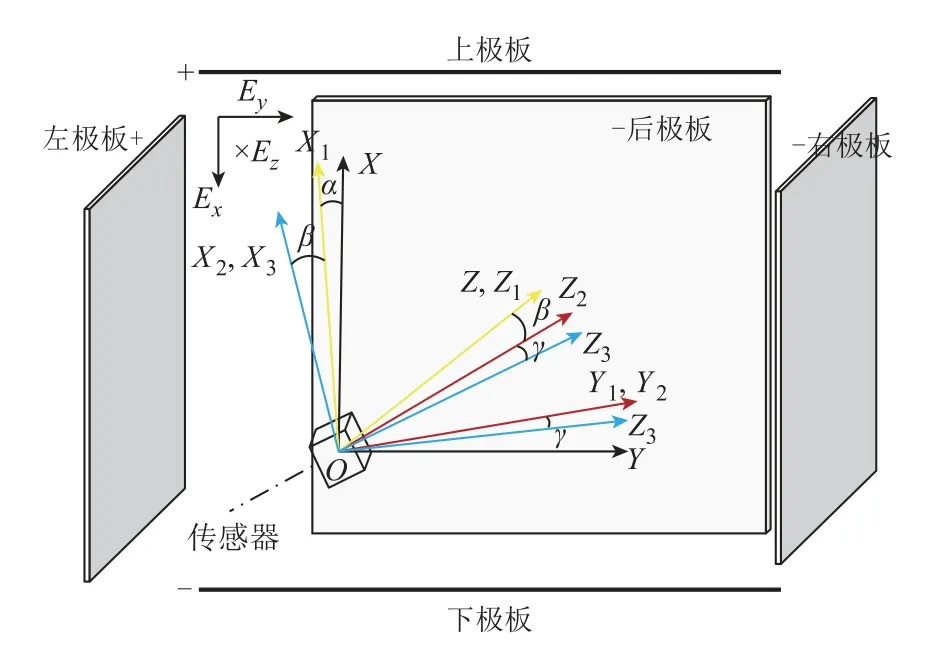
图4 三维电场标定装置示意图Fig.4 Diagram of 3D electric field calibration device

可得坐标系转换第三矩阵为

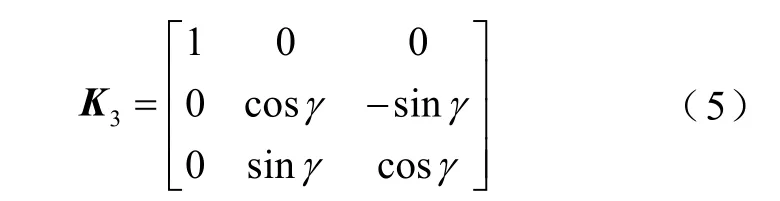
综上，得到了总的坐标系转换矩阵。XOYZ和X′OY′Z′两个坐标系下电场强度的关系公式为

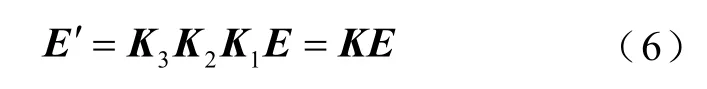
式中，E′为传感器所处空间位置处的电场强度；E为标定装置所产生的电场；坐标系变换矩阵K为

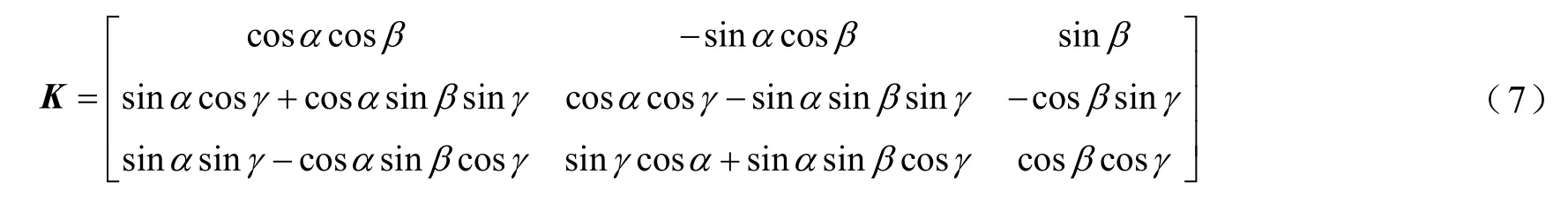
1.3 解耦标定方法

所设计的三维电场标定装置如图4所示，该图为平行于XOY平面的剖面图（与后极板相对应的前极板未标出，固定及驱动传感器转动的装置未标出）。传感器在电场标定装置中的姿态角为α、β和γ。

因此，可以得到传感器的输出方程为

上述模型需要求解的是标定方程中的灵敏度系数矩阵。在三维电场标定装置中，可以给出在三个坐标轴方向均可调的电场的强度，为简化计算，将(ExEyEz)′取单位电场强度(1 0 0)′，便可得出一组三个方向上的传感器输出的电压值，分别记为Ux1、Uy1、Uz1；同理，再分别令(ExEyEz)′取(010)′和(001)′，得到另外六个电压值，分别记为Ux2、Uy2、Uz2；Ux3、Uy3、Uz3。将三次输出写成矩阵的形式，即可得到出传感器输出电压矩阵。

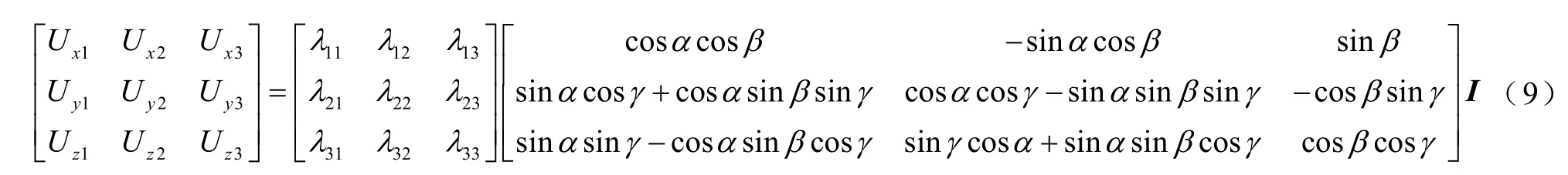
式中，I为场强组成的单位矩阵，则有

因K是正交矩阵，所以K一定可逆。

理论上，在整个标定过程中，灵敏度系数矩阵是不变的，即多次测量得到的灵敏度系数矩阵应该相同。但在实际中，由于存在测量误差，每次测量得到的灵敏度系数矩阵都会存在一定差别，因此需要进行多次测量。测量次数越多，得到的灵敏度系数矩阵越接近传感器的真实值。

1.4 标定流程

根据上述标定方法，可确定如图5所示标定流程。

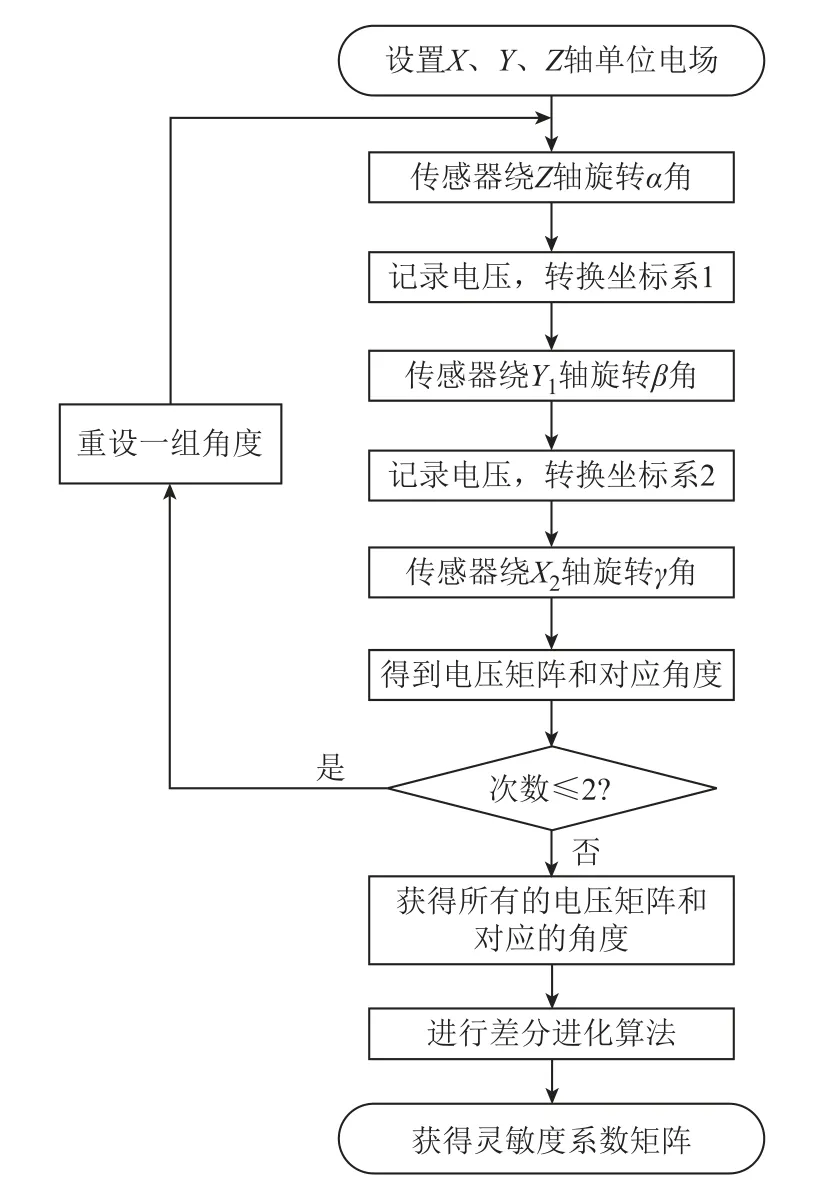
图5 三维电场标定方法流程Fig.5 Flow chart of three-dimensional electric field calibration method

2 基于差分进化算法的解耦方法

在进行多次测量过后，每一组测量数据U都可以通过乘以K-1的方式得到λ矩阵，这些表达出来的λ矩阵应该相同。因此，可以通过数次测量，使用某种寻优算法来获取灵敏度系数矩阵的近似解。

2.1 算法设计

给出若干组电压测量值，算法从若干组随机的角度点对（α,β,γ）开始，分别用对应的电压测量值矩阵乘以对应的坐标系转换矩阵的逆，得到若干灵敏度系数矩阵；可以将其写成一个向量，计算这些灵敏度系数矩阵之间的L距离，定义目标函数。

以三次测量为一组，记第i次测量值给出的数据计算得到的λ矩阵为λi，定义目标函数F为

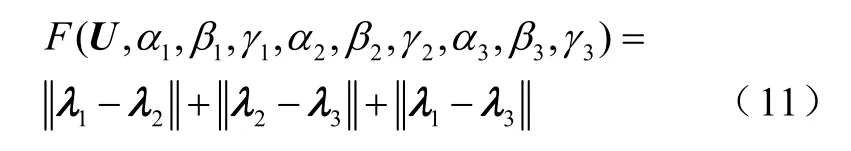
由于角度变化如何影响坐标系转换矩阵的变化尚未明确，因此考虑使用随机搜索算法。随机搜索算法常见的有遗传算法（Genetic Algorithm,GA）、粒子群算法（Particle Swarm Optimization,PSO）、差分进化算法（Differential Evolution,DE）和模拟退火法（Simulated Annealing,SA）等。

在文献[21-23]中，分别对DE、GA、PSO、SA算法进行了系列实验分析，DE算法均获得了最优的性能。DE算法简单强大，收敛迅速稳定，控制参数少，且参数设置对结果影响不明显因而易于实现，可以快速准确地解决高维问题。在本算例应用中，坐标系转换矩阵中的元素均为三角函数的四则运算，在形式上更接近多峰函数，DE算法由于变异过程的存在，有一定概率跳出局部最优值，具有强大的全局寻优能力，更适合多峰函数的情况[24]。

综合以上因素，选择使用随机搜索算法中的差分进化算法。

2.2 算法步骤

DE算法步骤包括解向量的变异（Mutation）、交叉（Crossover）、选择（Selection）三种操作。

DE算法的主要思路是：

1）种群初始化。在求解空间中随机并且均匀地产生若干个体，每个个体xi(0)在本例中都由9维向量构成。

2）向量变异。在第g次迭代中，从种群中随机选择三个个体在寻优策略下，生成变异向量Hi(g)。其中，缩放因子的最大值为1，缩放因子最小值为0.5；初始缩放因子取0.5，能够将上述随机选择的三个个体进行适应度从优到劣的排序。

3）向量交叉。选取变异向量Hi(g)与种群中的同代个体xi进行交叉。本例中交叉概率的值为0.7。

4）最优个体选择。比较试验个体与原父代个体的适应度函数，实现最优个体的选择。

DE算法的流程如图6所示，其中，满足终止条件指达到最大迭代次数，在本例中设置为5 000。

图6 差分进化算法流程Fig.6 Flow chart of differential evolution algorithm

在使用该方法校准传感器时，只需将传感器任意方向地在标准电场中旋转n组，每组三次旋转，得到3n个电压值；同时，粗略地测量这3n个角度，得到3n个角度的粗略值；输入3n个电压值和3n个角度的角度范围，比如粗略值左右各20°。这样，经过许多次迭代，算法就能找到灵敏度系数矩阵的近似值。

3 三维电场精确度分析

3.1 算法精确度检验

本文中使用python中Scipy库。Scipy库可以处理优化、插值、常微分方程数值解的求解等问题。使用Scipy库中的Optimize模块，参数设置如下：取初始种群大小为50；取变异时的缩放因子为（0.5,1）中的值，并随每一代个体进行自适应性调整；取交叉时的交叉概率为0.7。

矩阵之间的距离，定义为矩阵对应元素做差所得到的差矩阵的度量。根据不同的范数定义如L（1各元素绝对值之和），L2（各元素平方和的平方根），可以相对应地得到矩阵的L1距离和L2距离分别为

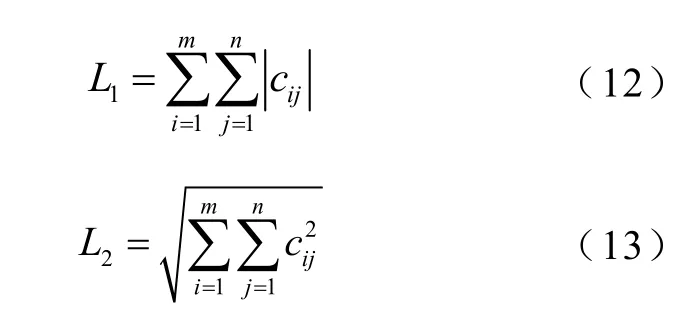
式中，cij为两个矩阵对应元素做差所得到的差矩阵C(m×n）的第i行第j列的元素。

使用同一组数据分别定义式（12）和式（13）的两种目标函数，获得采用距离L1和距离L2定义的灵敏度系数差值的对比数据，如图7所示，以测试更适合的目标函数的定义。

图7 使用不同距离计算出的误差值Fig.7 Comparison chart of different distance

图7中，λ代表原给定的灵敏度系数矩阵，λ1代表以L1距离为优化函数求得的灵敏度系数矩阵；λ2代表以L2距离为优化函数求得的灵敏度系数矩阵。横轴共有9个离散的点，分别为灵敏度系数矩阵中相应元素的L1或L2距离值。可以看出，基于L1距离定义的目标函数效果较好。其原因在于，在三维空间中，到某一定点P的L2距离小于某一定值的点比L1距离下要多。除此以外，增加每组测量的测量次数、增加最大迭代次数等方法也可以提升算法的精确度。

以三次测量一组为例，检验该方法的精确性。

首先，假设

灵敏度系数的选取考虑了三维传感器的维间耦合，因此在灵敏度系数矩阵λ0的非对角线设置了较强的耦合。分别设定三组传感器的摆放角度，并基于该角度进行校准（每组三次）。

经过计算得到电压值矩阵的具体数值为

将电压值矩阵代入本文所述的解耦算法中，运用程序计算灵敏度系数矩阵，得到三个灵敏度系数矩阵，其值十分接近，仅在个别值的小数点第四位上有差异，取平均值可得

误差率σ% 定义为9个系数之间最大的误差，在本例中则为

经过多轮测试，在最大迭代次数为5 000的情况下，该方法均找到了误差率不大于3%的解。

3.2 标定方法优化

利用计算机仿真的便利，讨论精确度随角度取值范围的变化，优化标定方法。

由于α,β,γ∈[0,2π]，将每个角度的范围平均分成四份，测试角度在4×4×4个不同区域内算法的精确度，绘制α、β、γ属于不同范围时的误差率图像。

图8为误差率随α、β、γ取值变化范围。图中横坐标分别为α、β、γ取值；纵坐标为λ的三个值中最大的相对误差。

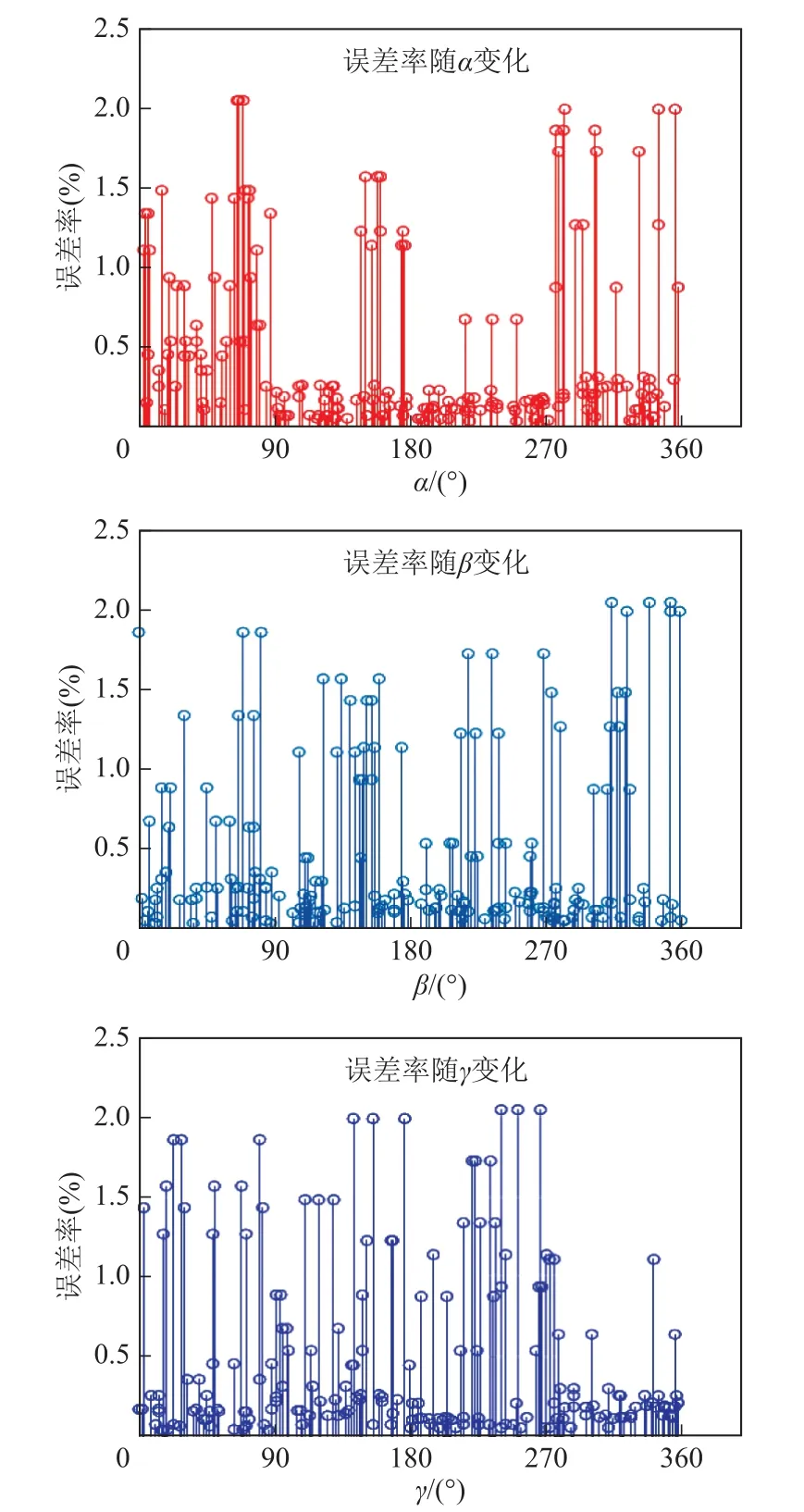
图8 误差率随角度的变化范围Fig.8 Variation of error rate with angle

由相对误差率的最大值点的变化可以看出，在进行标定时，最好角度的范围满足α∈[180°,270°]，γ∈[270°,360°]，β的取值范围对相对误差率的影响则不如前两者显著。这样可以进一步提升算法的精确度，避免出现某些个别值的误差率大于3%的情况。

将本文所提方法与其他方法对比，如遗传算法和模拟退火算法。不同算法之间的对比结果见表1。遗传算法和模拟退火算法的平均误差率和最大误差率均大于差分进化算法，其主要原因在于差分进化算法使用了变异和交叉策略，实现了新个体取代较劣个体，有助于跳出局部最优值，实现全局最优。

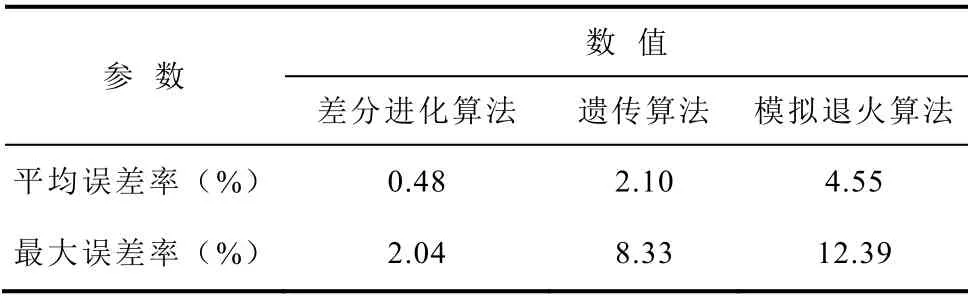
表1 不同算法误差率Tab.1 Comparison between algorithms

4 结论

为实现三维空间电场传感器的标定，本文构建了灵敏度系数与维间耦合和空间位置角度关系的数学模型，提出了一种基于差分进化算法的求解灵敏度系数矩阵的方法。该方法能够进行电场矢量传感器的维间耦合解耦及传感器校准的角度偏差校正，并简化标定装置设计的复杂度和难度，这是目前广泛采用的其他模型所不具备的。该方法也可为其他类型的三维传感器标定提供参考。研究结果表明：

1）在三维电场传感器的标定中，通过传感器空间角度信息及标准电场的电场强度值，就可以根据传感器的输出电压值求解出灵敏度系数矩阵。同时，为减少测量误差，需要进行多次测量校准。

2）通过选择恰当的目标函数和约束条件，构造运算效率高、鲁棒性强的差分进化算法，完成三维空间电场传感器灵敏度特性寻优，能较为精确、稳定和快速地求解。

3）在进行标定时，角度范围满足α∈[180°,270°]，γ∈[270°,360°]，可以进一步提升算法的精确度和标定的准确性。