基于径向基神经网络的多负载无线电能传输系统自适应阻抗匹配方法
吴月宝 赵晋斌 张少腾 张俊伟 汪学良
(1.上海电力大学电气工程学院 上海 200082 2.上海广为美线电源电器有限公司 上海 201100)
0 引言
无线电能传输(Wireless Power Transmission,WPT)技术由于其安全、可靠、便捷的优点,在电动汽车[1-3]、消费电子[4]、有轨列车[5-6]、植入式医疗设备[7]等领域具有巨大的应用前景,吸引了众多研究者的关注。随着无线电能传输技术的不断发展,学术界和产业界将其应用到越来越多的场景中,对传输功率、传输效率、传输距离等性能要求也越来越高。
多负载无线电能传输技术受到越来越多的关注,然而,其系统结构相对复杂,理论分析与优化是一个较大的挑战[8-9]。很多文献已对此项技术做了相关研究,包括传输特性分析[10-11]、效率优化[12-13]、提高传输距离[14]等。与单负载系统不同,当接收线圈距离较近时,多负载系统接收线圈之间将产生不可忽视的交叉耦合。交叉耦合会导致系统等效负载和谐振频率的变化,进而导致系统在电源频率处传输效率降低。针对此问题,以往的研究主要集中在以下两个方面:
(1)谐振频率跟踪。文献[15]在多发射线圈或多接收线圈WPT系统中存在交叉耦合的情况下,提出通过电力电子技术,实时调整电源频率,以实现最大传输效率的方法。但此方法受到ISM(industrial scientific medical)频段的限制,无法做到频率的任意调整。
(2)阻抗匹配。文献[16]提出在接收线圈与负载间插入阻抗匹配网络消除交叉耦合的影响,但未指出具体应如何实施,也无法做到实时对交叉耦合进行补偿。近年来,有学者采用智能算法实现自动阻抗匹配。文献[17]采用基于机器学习算法,自适应调整匹配网络参数以及选择发射线圈大小的方法,实现在10~25cm距离下,传输效率均保持在90%左右,但未考虑多负载的情况。文献[18]基于多层前馈(Back Propagation,BP)神经网络,通过步进电机调整匹配网络中的电容,实现了实时的自动阻抗匹配,在10~30cm范围内,传输效率均保持在78%左右,并取得了良好的动态性能。
基于智能算法的阻抗匹配实质上是对具有非线性特征的阻抗匹配网络的优化逼近。在智能算法中,RBF神经网络具有结构简单、学习速度快、逼近精度高的优点,非常适用于自适应阻抗匹配。
因此,针对多负载WPT系统中交叉耦合导致效率下降的问题,本文依据电路理论,建立多负载无线电能传输系统模型,深入分析接收线圈间交叉耦合对系统传输效率的影响机理,提出基于径向基函数(Radial Basis Fuction,RBF)神经网络实时调整阻抗匹配网络中电容的方法,提升系统与负载的匹配程度,进而提高了传输效率。
1 多负载无线电能传输系统
1.1 系统模型
图1展示了典型的多负载无线电能传输系统,Vs为高频电源,Zs为电源内部阻抗,CT和CR1,…,CRn分别是发射线圈和接收线圈的补偿电容,LT和LR1,…,LRn分别是发射线圈和接收线圈的自感,RT和RR1,…,RRn分别是发射线圈和接收线圈的寄生电阻,ZL1,…,ZLn是各接收线圈的负载,MT1,…,MTn,M12,…,MTn,为各线圈两两之间的互感,Zeq为等效负载。
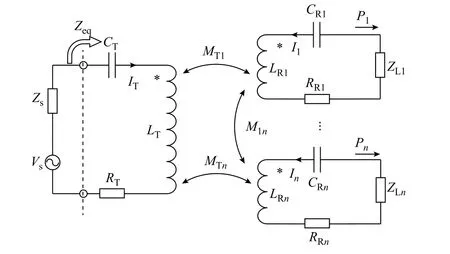
图1 典型多负载无线电能传输系统Fig.1 General multi-load WPT system
根据基尔霍夫电压定律(KVL),双负载无线电能传输系统可用矩阵方程组表示为
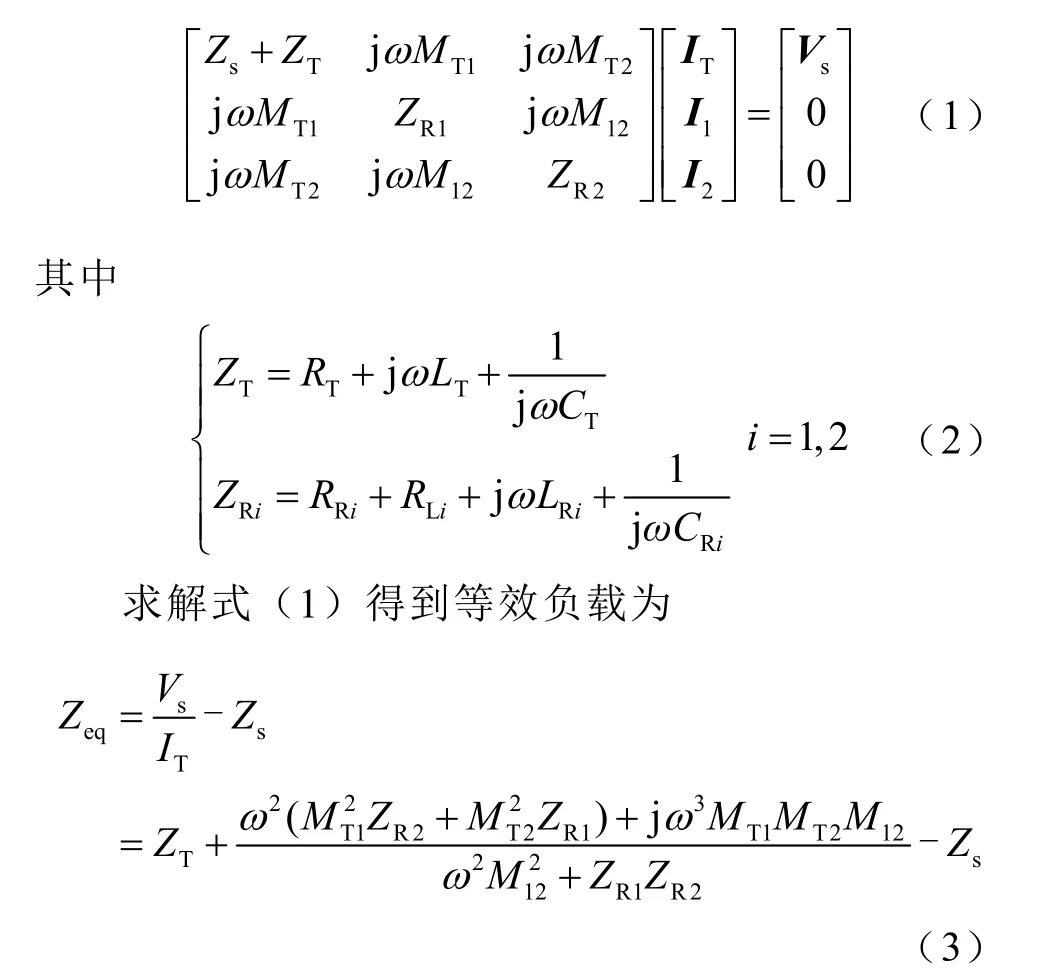
由式(3)可知,系统等效阻抗Zeq随着耦合电感及负载的变化而发生变化。在发射线圈和接收线圈均调谐的情况下,由于交叉耦合M12不为零,Zeq将出现虚部,变为非纯阻性等效负载。
进一步可求得各线圈电流为
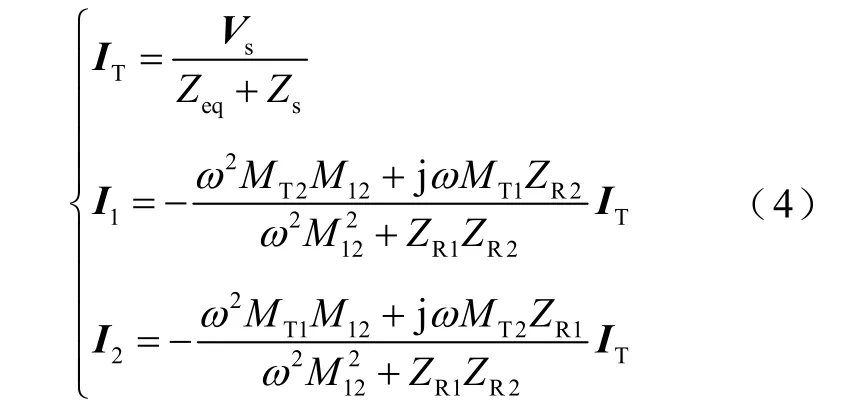
可求得系统传输功率Po为
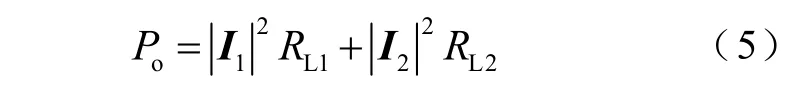
可求得系统传输效率η为
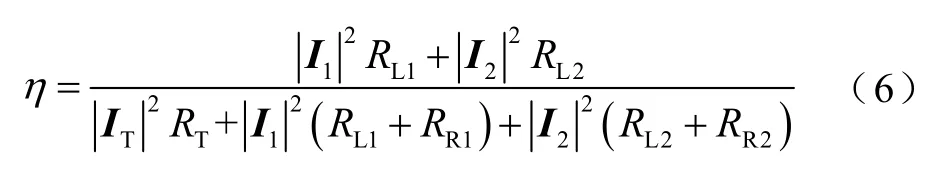
三负载及以上系统的分析与双负载类似,为不失一般性,本文给出了N个负载WPT系统的分析过程,具体请见附录。N个负载与双负载的分析结果均表明:交叉耦合导致系统等效负载由纯阻性变为非纯阻性。
1.2 交叉耦合影响
本节以双负载无线电能传输系统为例讨论交叉耦合对系统传输效率的影响。根据1.1节建立的模型和推导过程,本文在Matlab中编写了系统传输效率的计算程序,得到系统传输效率如图2所示,频率响应如图3所示。电源频率设为6.78MHz,为分析方便,发射线圈与两接收线圈参数完全一致,负载相同。各线圈之间的耦合系数可表示为
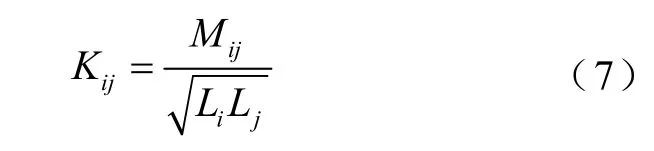

图2 系统传输效率Fig.2 System transmission efficiency
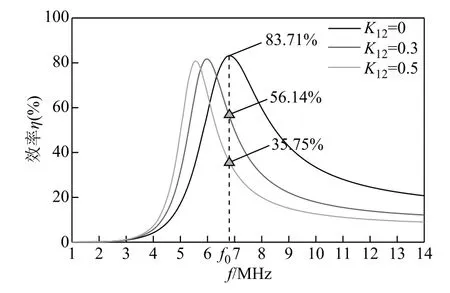
图3 频率响应(KT1=KT2=0.1)Fig.3 Frequency response(KT1=KT2=0.1)
由图2可知,系统传输效率受到接收线圈之间交叉耦合系数K12的影响,随K12增大而减小。且交叉耦合系数一定时,发射线圈与两个接收线圈之间的耦合系数KT1和KT2越小,效率下降越多。这表明当发射线圈与接收线圈之间的耦合越弱,交叉耦合对系统传输效率的影响越大。
图3给出了KT1=KT2=0.1,不同交叉耦合程度下,系统传输效率对频率的响应。如图所示,交叉耦合增大,系统谐振频率产生偏移,导致系统传输效率在f0处传输效率降低。K12为0.3和0.5时,传输效率仅分别为56.14%和35.75%,且交叉耦合系数K12越大,效率下降越多,取得最高效率时的频率不再是电源频率。另外,偏移后的效率峰值也低于未偏移的效率峰值,这意味着通过调整电源频率的方法只能够改善效率,而不能完全补偿效率损失。
综上所述,在多负载无线电能传输系统中,接收线圈之间的交叉耦合,实质上是等效于改变了各个接收线圈的电感值,破坏了谐振条件,导致接收线圈的固有谐振频率发生了变化,最终引起系统失谐,无法在电源频率处以最高效率进行能量传输。同时,交叉耦合改变了系统的等效负载,造成系统电源阻抗与负载阻抗的不匹配。
2 “T”型阻抗匹配网络
2.1 “T”型阻抗匹配网络结构
针对以上问题,本文提出在电源与等效负载之间加入“T”型阻抗匹配网络,如图4所示。与文献[13]相似,本文采用开关切换电容的方法实现电容的调整,但使用了更少的电容,降低了控制系统的要求。电容可切换的“T”型阻抗匹配网络,L1、L2为固定电感,C1为固定电容,C2、C3为可调电容。其中C2、C3分别由多个开关控制的电容并联组成,通过控制开关的闭合与打开来调整C2、C3的容值大小,即所有闭合开关对应的电容值之和,即,若开关S2_1,S2_2,…,S2_k闭合,则电容C2的值为

图4 “T”型阻抗匹配网络Fig.4 “T”type impedance matching network
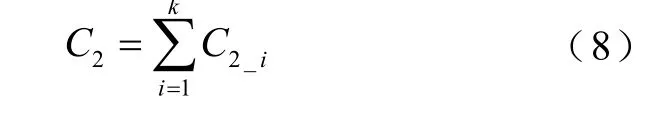
电容C3的计算方法与C2相同。
根据电路理论,可求出此时电源侧的输入阻抗Zin为
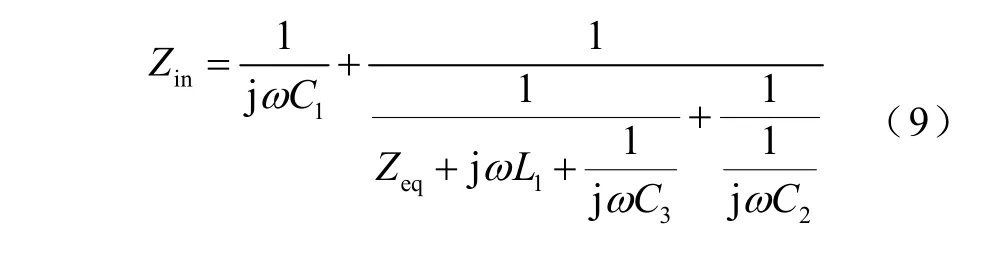
2.2 “T”型阻抗匹配网络匹配特性
在高频电路中,常采用输入反射系数S11来表征电源端口与负载端口之间的匹配程度,S11为
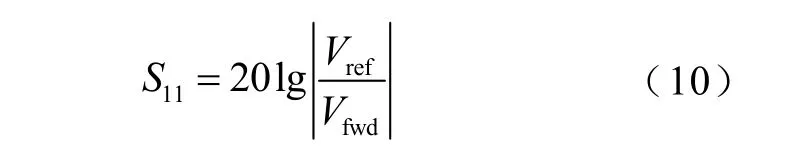
式中,Vref为反射电压;Vfwd为入射电压。S11越小,匹配程度越好,系统损耗越小,一般建议S11<-20dB。
由式(9)可知,通过改变C2、C3的值即可改变加入匹配网络后的输入阻抗Zin,实现电源阻抗与输入阻抗互为共轭。图5给出了不同负载阻抗时,S11与C2、C3之间的关系。表明在特定负载阻抗下,C2、C3在一定范围内变化时,总存在一个最小的S11,即图中颜色最深的点,此时电源与负载的匹配程度最好。
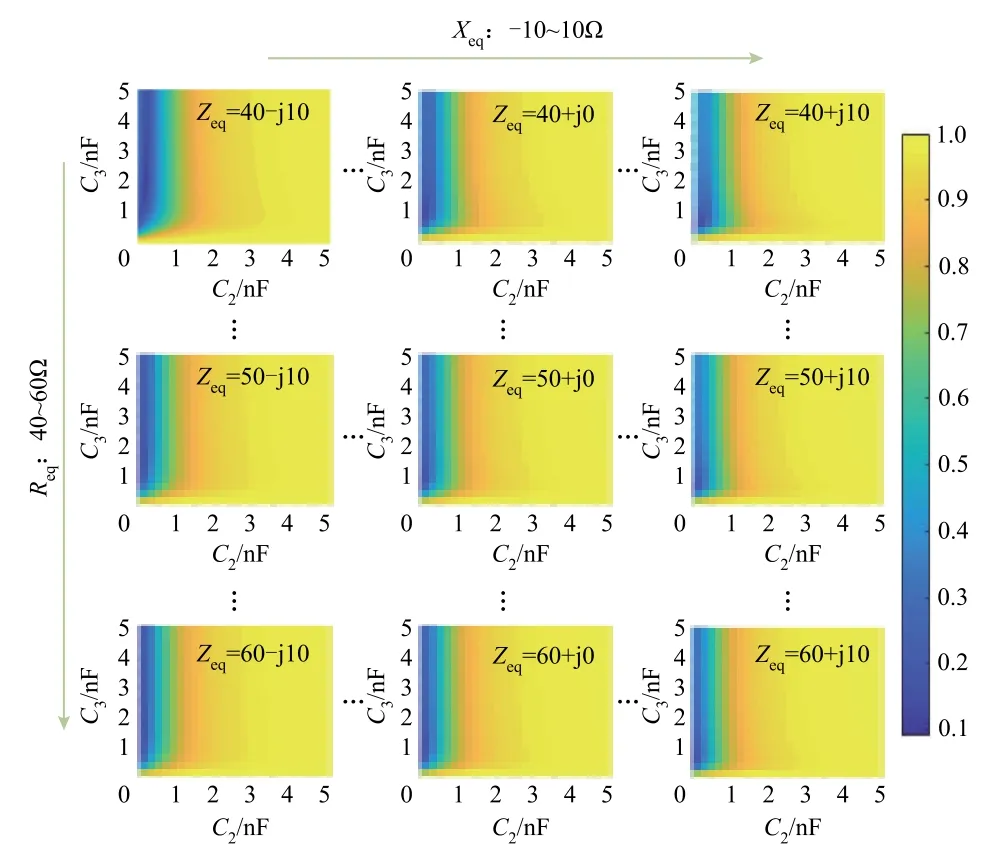
图5 |Vref/Vfwd|与电容C2、C3的关系Fig.5 The relationship of capacitor |Vref/Vfwd| and C2,C3
3 RBF神经网络
RBF神经网络相比于传统的BP神经网络,结构简单,具有更少的隐含层,学习速度快,且具有局部搜索能力,避免了BP神经网络的局部极小值问题。对非线性连续函数具有良好的近似能力,广泛应用于非线性网络的逼近。
3.1 RBF神经网络结构
图6为典型的RBF神经网络结构示意图,X=[x1x2…xP]T,Y=[y1y2…yQ]T分别是输入向量和输出向量。输入神经元个数P等于输入向量维数,隐含层神经元数M等于训练数据个数。基函数采用高斯函数为
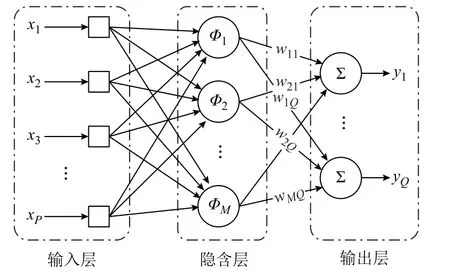
图6 典型的RBF神经网络结构Fig.6 Typical RBF neural network structure
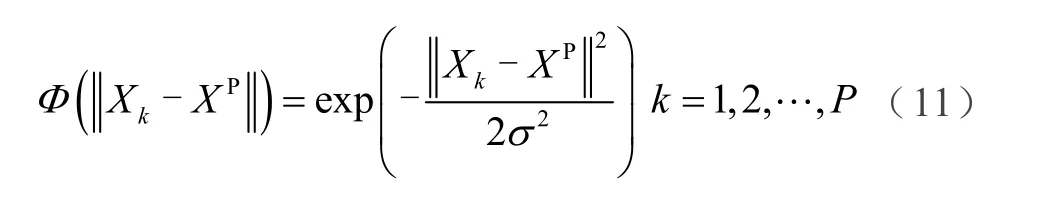
式中,XP为隐含层基函数中心;σ为隐含层基函数标准差。
3.2 RBF神经网络训练算法
RBF神经网络需要训练的参数主要有三个:基函数中心XP,隐含层基函数标准差σ和隐含层到输出层的权值ω。
1)确定隐含层基函数中心XP
基函数中心采用k-均值(k-means)聚类方法确定。相比于随机选取基函数中心,采用k-means聚类方法更为合理。算法步骤如图7所示。
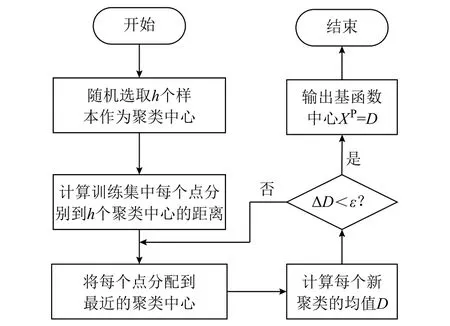
图7 k-means聚类方法确定XP步骤Fig.7 The flow chart of the k-means clustering method
2)确定隐含层基函数标准差σ
根据高斯函数标准差公式为

式中,cmax为所选取聚类中心之间的最大距离;h为选取样本数。
3)确定隐含层到输出层的权值ω
隐含层到输出层的权值采用梯度下降法训练。首先利用代价函数为

式中,E为某一输出神经元的误差;M为训练样本个数;ek为第k个训练数据与其期望值yk之差。
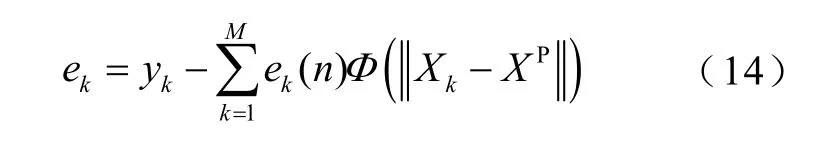
根据梯度下降法基本原理,可求得梯度为

式中,ωi(n)为第n次迭代的权值。
进一步可求得权值为
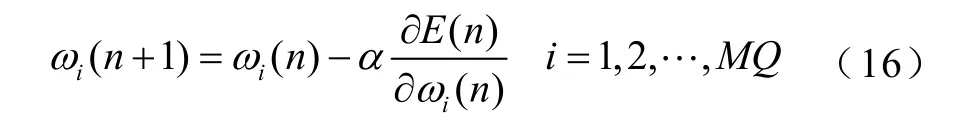
式中,α为学习率,取α=0.1。
故输出层第q个神经元输出结果Yq为
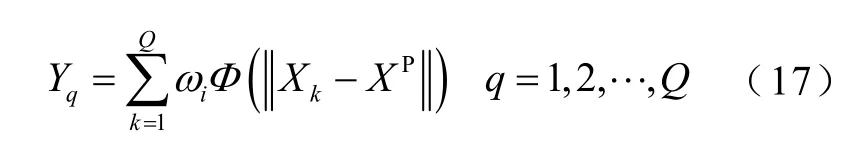
3.3 RBF神经网络训练及测试
根据3.2节中的学习算法,本节介绍如何训练RBF神经网络预测C2、C3最优值。由于RBF神经网络具有逼近任意非线性网络的特点,因此,可以建立等效负载(Req,Xeq)与阻抗匹配网络中的(C2,C3)的映射,利用RBF神经网络逼近这种映射关系。具体如图8所示。
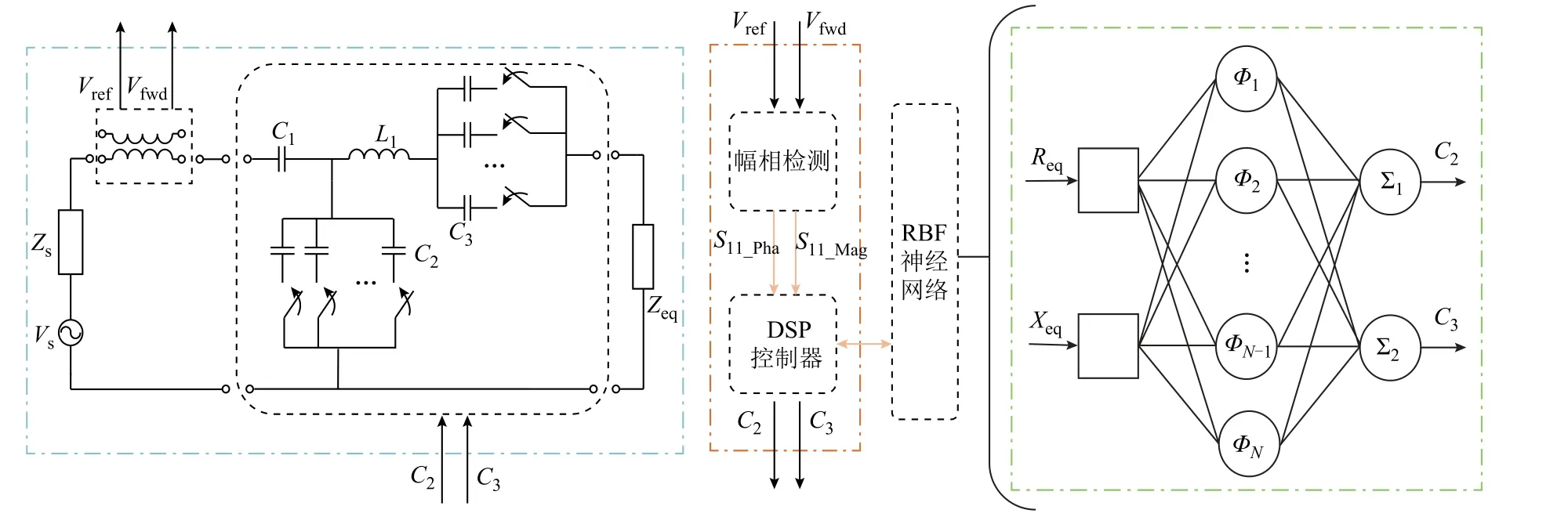
图8 系统控制框图Fig.8 The control diagram of the system
训练与测试数据请见表1,比例约为8:2。表1中的阻抗值作为训练数据的输入量,采用与实验装置一致的参数,依据式(10)计算出1 701个样本在电容可调范围内的反射系数最小值S11_min,并将每个样本的S11_min相对应的最优电容值C2_opt、C3_opt记录下来作为训练数据的输出量,这样就得到了RBF神经网络的训练数据。利用这些数据对网络进行训练,采用同分布的测试数据对训练完成的RBF神经网络进行测试。


表1 训练与测试数据Tab.1 Training and test data
图9a、图9b分别给出了RBF神经网络对C2与C3测试结果的相对误差。作为对比,BP神经网络算法的测试结果也同时给出。无论是C2还是C3,RBF算法的测试结果均优于BP算法。平均相对误差请见表2。
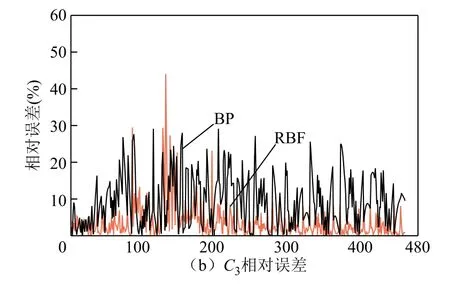
图9 C2与C3的相对误差Fig.9 The relative error of C2 and C3

表2 RBF与BP算法的平均相对误差Tab.2 The mean relative error of RBF and BP
3.4 等效负载误差对预测结果影响
为了衡量等效负载误差对预测结果的影响,本文将表1中测试数据分别对原值变化±3%、±5%、±8%、±10%,作为输入数据,利用训练完成的RBF算法进行测试,将测试结果与原值的测试结果对比,并计算了各个数据的反射系数。结果如图10所示。
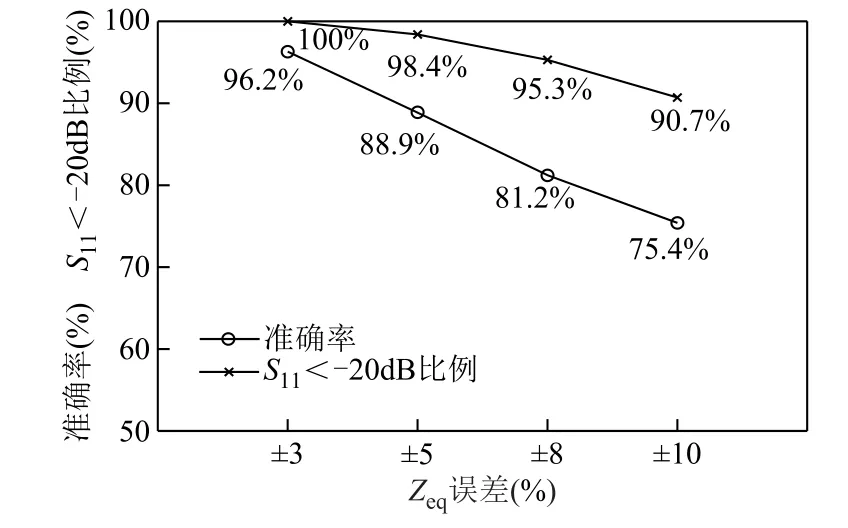
图10 Zeq误差对预测结果的影响Fig.10 The influence of Zeq error on prediction results
在等效负载偏差10%时,预测结果有约75%的样本得到了最优值,然而,取得良好的匹配效果(S11<-20dB)的比例却达到了90%。这是由于预测结果虽然不是最优值,但接近最优值,此时同样可以达到较好的匹配效果。综上所述,等效负载误差虽然对电容预测结果有一定的影响,但最终对系统匹配性能的影响相对较小。
4 实验验证
为了验证所提方法的有效性,本文搭建了如图11所示的实验平台。信号发生器与功率放大器组成高频电源,定向耦合器(1~50MHz,耦合度25dB,方向性30dB)采集电路入射电压与反射电压,并提供给幅相测量电路AD8302(幅值:30mV/dB,相位:10mV/(°))。控制器为DSP(TMS320F28335,150MHz),根据AD8302处理得到的反射系数S11幅值和相位,得到等效负载值,DSP内置已经训练完成的RBF神经网络,这样即可得出最优的电容值,并将对应的控制信号发送给各继电器,实现电容C2和C3的实时调整。阻抗匹配网络中电容C2和C3分别由四个电容并联组成。系统具体参数见表3。

表3 实验系统参数Tab.3 Component parameters in experimental setup
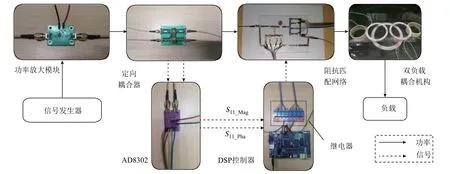
图11 实验装置Fig.11 Experimental setup
发射线圈与接收线圈的相对位置如图12所示。由图12可知,发射线圈位于两接收线圈下方,发射线圈与接收线圈2相对位置保持不变,接收线圈1的圆心围绕与发射线圈同心的圆逆时针运动。发射线圈与两接收线圈的耦合系数不变,两接收线圈之间的耦合系数K12将随着θ(0→π)的变化而变化。
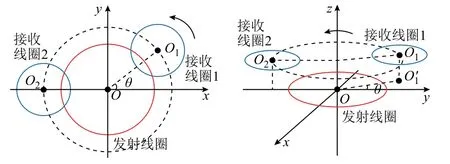
图12 发射线圈与接收线圈的相对位置Fig.12 The position of the transmitter and the receivers
图13给出了匹配前后K12分别为0.1、0.2、0.3、0.4、0.48时输入阻抗的变化情况,不同交叉耦合系数下,匹配后的输入阻抗均在史密斯圆图的中心附近,与目标阻抗50+j0Ω较为接近,提升了电源阻抗与负载阻抗的匹配程度。
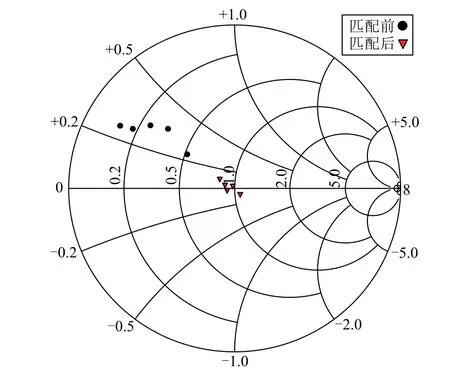
图13 匹配前后输入阻抗Fig.13 The input impedance before and after matching
图14a给出了加入自适应阻抗匹配网络前后的传输效率。由图14可知,匹配后的效率在不同的交叉耦合系数下均获得提升。当两接收线圈完全重叠时,此时交叉耦合系数最大(K12_max=0.48),系统传输效率从最低时的34%提升到了78%。
图14b给出了加入自适应阻抗匹配网络前后的频率响应,其中包括实验值与计算值。由图可知,加入后的效率峰值被修正到6.78MHz附近,谐振频率处的系统效率获得较大提升,降低了交叉耦合的影响。值得注意的是,匹配后的系统传输效率无法稳定地保持在K12=0时的水平,主要原因是阻抗匹配网络的电容值是离散的,无法将阻抗匹配网络的参数调整到匹配范围内的任意值。虽然可以通过增加电容数量的方式提升效率,但元件的增多会导致系统成本增加,同时提高了控制系统的复杂度,降低了实用性。所以在这两者之间取得合理的平衡是一个很重要的问题。
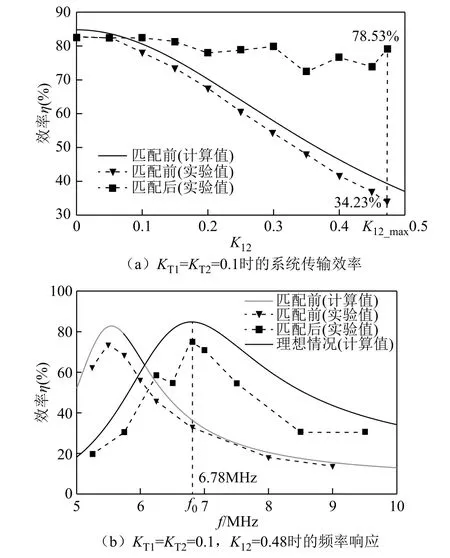
图14 实验效率与频率响应Fig.14 The efficiency and frequency response
此外,等效负载的检测精度也是一个需要考虑的问题,这直接影响RBF神经网络算法的预测精度。表4给出了检测值与理论值误差,由表4可知,测量误差均在10%以内,为神经网络的准确预测提供了较好的基础。
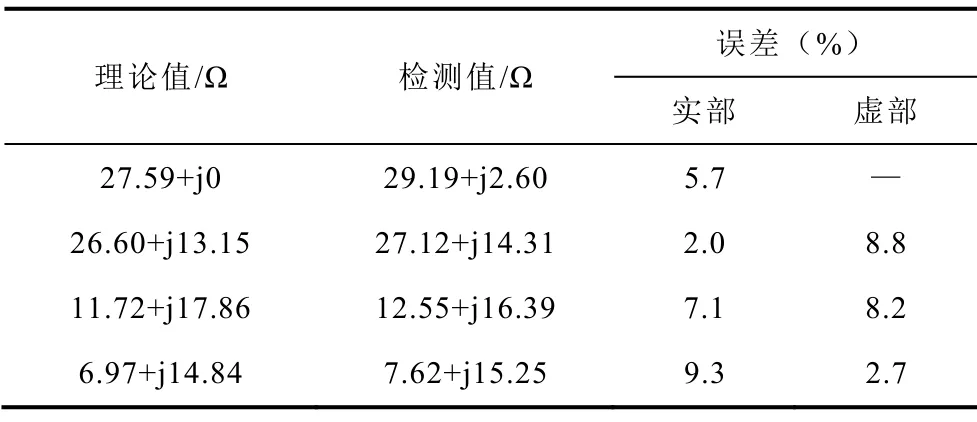
表4 测量误差Tab.4 The measurement error
5 结论
针对多负载无线电能传输系统中交叉耦合导致系统传输效率下降的问题,本文通过理论分析、数值计算和实验验证,得到以下结论:
1)多负载系统交叉耦合的存在使得系统传输效率下降,且发射线圈与接收线圈的耦合越弱,交叉耦合越强,效率下降越严重。
2)本文提出基于RBF神经网络算法的“T”型阻抗匹配网络,通过开关切换实现网络中电容的调整。实验结果表明:在不同交叉耦合强度下,加入自适应阻抗匹配网络的系统,传输效率均获得有效提高。在交叉耦合系数最大时,效率从最低时的34%提升至78%。
3)本文将智能算法应用到多负载WPT系统自适应阻抗匹配中,为解决此类问题提供了新思路。发射线圈与接收线圈的相对位置的改变(传输距离和角度的变化)、终端负载的变化等导致系统等效负载发生相应变化时,都可以采用自适应阻抗匹配的方法来提高系统传输效率。
附 录
根据基尔霍夫电压定律(KVL),N负载系统可用表示为
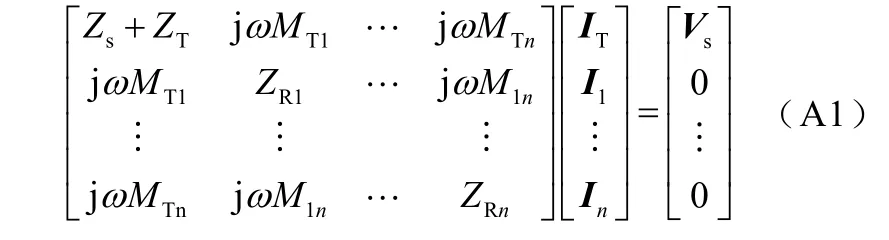
为方便表述,式(A1)可写为

其中,矩阵Z可以写成
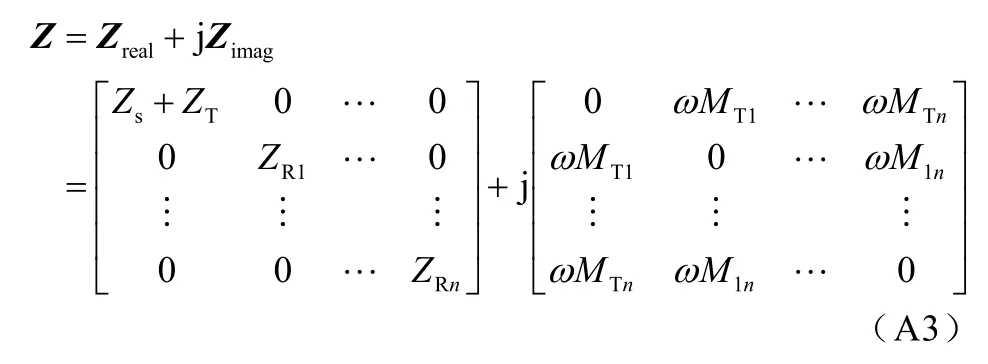
在发射线圈和接收线圈均完全调谐的情况下,Zreal为实数矩阵。各个线圈之间的互感均不可忽略,所以Zimag除了对角线元素外,均不为零。Zimag也是实数矩阵。
求得各个线圈中的电流为
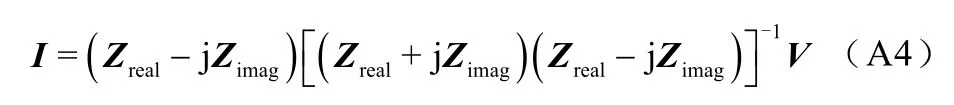
由于ZrealZimag和ZimagZreal均为零矩阵,所以
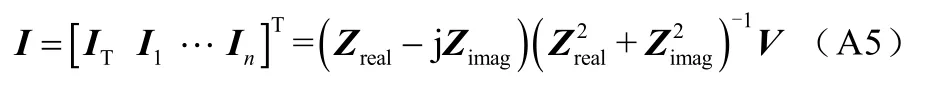
电流向量I的任一元素IT,I1,…,In的虚部均不为零。
进一步求得系统等效负载为

同理,等效负载虚部不为零,由纯阻性负载变为非纯阻性负载。
可求得N负载系统功率和效率分别为


