基于FAVAR模型的技术创新效率不确定性测度

王必好，梁荣成

(1.华东交通大学经济管理学院，江西 南昌 330013;2.中国人民大学劳动人事学院,北京 100872)

0 引言

中国经济已经转向高质量发展阶段，必须推动经济发展质量变革、效率变革、动力变革。技术创新效率变革在 “三大变革”中发挥先导性作用，受大量随机因素影响，许多不可观测变量会发生不确定性变化，表现为自回归扰动项变动幅度较大。因此，如何测度技术创新效率不确定性程度，提高测度结果精准化水平是一个很好的研究选题。尤其是，研究测度上市公司在产业层面的技术创新效率不确定性程度，分析股价指数、时期长度、创新要素投入、新产品产出等信息在这种不确定性变动中的作用，使测度结果能准确反映技术创新效率不确定性的变动幅度与特征。

测度技术创新效率不确定性程度，在观察时期长度、信息获取、模型构建、方差分解等方面存在许多可以深入研究的问题。本文以上市公司技术创新效率不确定性测度作为重点内容，研究技术创新效率在哪个时期保持最优状态，引入哪些变量或变量组合可以准确反映技术创新效率实际变动情况，能否在创新要素投入与产出环节中提炼出共同因子，识别与吸纳更多技术创新效率变动信息，探索技术创新效率不确定性测度结果有哪些构成，可以细化分解为哪些影响效应，从而提高测度结果精准化水平。

基于此，本文重点研究3个方面：①运用主成分分析方法，从大量数据集合中提炼共同因子，吸纳更多信息，全面准确反映技术创新效率变动趋势。②建立因子增广向量自回归模型 (FAVAR)，把创新要素投入与产出环节中大量数据集合分为两种变量，即共同因子和反映其额外信息的不可观测变量，构建技术创新效率预测器，获取更多技术创新活动信息。③运用脉冲响应和方差分解方法，分析共同因子等影响因素的单位扰动项冲击导致技术创新效率变动幅度，测度每一次冲击对技术创新效率方差的贡献份额及其相应的时期长度，真实反映技术创新效率不确定性程度。本文的理论贡献在于，更加真实反映技术创新效率不确定性变动的来源、生成过程以及扩散传导，进一步提高不确定性测度精准化水平，引导创新主体选择合理的创新要素投入阶段，改善投入产出比例，实现最优技术创新效率，在此基础上提出相关政策建议。

1 文献综述

1.1 技术经济现象不确定性测度

不确定性技术经济现象研究，主要通过单一变量波动幅度和离差反映其变动情况，运用VAR方法估计，变量新息 (Innovation)测度结果表明，不确定性对产出和雇工在6个月内仍然产生作用[1]。实际经济活动的不确定性变动，由不同厂商、不同产业盈利、TFP与预测量离差作为衡量变量，经济衰退是由不确定性增加所引起的，进而导致生产率下降[2]。这些研究认为不确定性变量具有明显的随机变动特征，而德国调查公司数据分析发现，不确定性出现是衰退的结果而不是原因[3]。早期不确定性问题研究的重点是各种测度方法[4]，即使测度结果是无偏的，分析者对测度结果的分歧不等于其具有不确定性[5]。国内学者构建中国季度宏观经济政策分析模型，研究1996—2007年经济运行不确定性特征[6]。然而，导致技术经济现象不确定性因素及构成份额受到多种因素影响，本文将在增加信息量、模型升级以及实证方法改进等方面深化研究，拓展对不确定性现象的认识。

1.2 FAVAR模型建立与应用

VAR模型的分析功能是通过与因子分析相结合而得以拓展[7]。共同因子和因子增广向量自回归模型 (FAVAR)具有处理高维度时间序列数据的优势，动态因子包含着丰富的宏观经济信息，解释产出、就业、价格等主要变量的大部分方差[8-9]。提取的因子可以视作宏观经济变量，从而扩大FAVAR模型的应用领域[10-11]。国内学者[12]以FAVAR模型测度2003—2016年中国经济不确定性，分析中国货币政策的宏观经济效应[13]，计算中国CPI宏观成分并且揭示宏观冲击效应[14]。与上述文献不同，本文以沪深股市6个产业上市公司技术创新活动信息集为主要数据来源，利用FAVAR模型在处理高维度数据方面的优势，测度技术创新效率不确定性程度，进而应用脉冲响应函数，揭示共同因子和不可观测变量对技术创新效率的冲击效应，以新的研究视角和方法，对不确定性方差进行结构性分解，提高测度结果精准化水平。

1.3 技术创新效率不确定性变动及影响因素

吸纳应用先进技术并不一定带来要素集约利用，其效率变化具有随机性特征[15]。技术升级在高、中、低3个阶段中是不确定的，其投入产出比例随机变动特征明显[16]。技术创新效率随机变动加大其离散程度，由标准方差表示，并可运用统计指标进行调整[17]。国内学者[18]从制度性改革角度分析未来中国全要素生产率 (TFP)增长潜力和驱动因素，研究政策实施过程中风险和不确定性。长期和短期机构投资者的技术创新效率有着显著差异， “短视论”不能解释机构投资者的投资行为[19]。全要素生产率提升的3个途径是技术进步、技术效率提升和结构转换[20]。然而，技术创新效率不确定性受到自变量扰动项的冲击，可以运用主成分分析方法提炼共同因子，构建FAVAR模型进行理论分析，最大限度地吸纳技术创新活动信息，从而定量测度技术创新效率不确定性。

上述文献中，技术创新效率研究与不确定性测度主要依靠单一指标，通过单变量离差、时间序列无条件波动和回归扰动项进行分析。本文创新点在于，把因子分析 (FA)与向量自回归分析 (VAR)结合起来，把不确定性看作是不可观测变量的变动结果，在投入产出两个环节中吸纳更多技术信息。通过提炼共同因子，有效扩大信息量，精准测度技术创新效率不确定性程度。引入脉冲响应函数，分析自变量每单位方差带来因变量方差的变动幅度，更准确地反映变量之间的冲击程度与响应关系，精准测度技术创新效率不确定性变动特征。

2 理论模型分析

2.1 提炼共同因子

本文把不确定性测度模型[21]应用到技术创新效率研究领域。假设St= (S1t,…,SNt)′为技术创新活动中大量数据集合，既包含技术创新效率不确定性变动的共同因子，也有不可观测变量，对St进行对数或微分变换，保证序列稳定性。通过以下形式，在Sit中提炼共同因子，获得不可观测变量的信息,公式为：

(1)

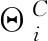
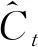
(2)

2.2 构建技术创新效率FAVAR模型

(3)

(4)

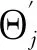
2.3 基于FAVAR模型的技术创新效率不确定性测度

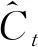
(5)

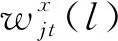
(6)

根据以上分析形成研究思路Ⅰ：因子增广向量自回归模型 (FAVAR)运用主成分分析方法，从大量数据集合中提炼共同因子，与滞后l时期长度的技术创新效率同时纳入自回归分析，采集不可观测变量的更加完全信息，回归扰动项变换为不确定性测度方差，经过正交化后求得平方根，反映技术创新效率不确定性程度。

2.4 技术创新效率不确定性程度的方差分解

技术创新效率预测器Mit是主要影响因素，存在着许多直接或间接变量，导致技术创新效率不确定性变动，新的扰动项又加剧这种不确定性变动。对其中的共同因子Ct(不可观测变量At的讨论也是相似的)进行自回归分析，模型可表示为：

(7)

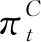
ΔC(l)=ΔC(l-1)+ (ΘC)2 (l-1)(ζC)2

(8)

式中，共同因子Ct引起技术创新效率不确定性测度方差ΔC(l)变化，主要受到时期长度l及其方差 (ζC)2的冲击作用。特别地，共同因子Ct对技术创新效率不确定性变动形成的冲击效应可以通过其方差 (ζC)2自回归分析进行细化分解，对数化消除可能的异方差，模型可表示为：

(9)

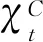
共同因子Ct方差 (ζC)2在t时期和t+l时期之间可以细化分解为n阶段，每个阶段对不确定性的冲击仍然存在着3种效应，即水平效应μC、规模效应ρC和稳定性效应ηC。在每个阶段中，后一时期冲击效应都是独立于前一时期，共同因子Ct导致技术创新效率不确定性具有随机特征，期望方差随机变动可分解为：

(10)

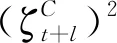
根据以上分析形成研究思路Ⅱ：提炼的共同因子纳入FAVAR模型分析，获取不可观测变量的更多信息，对技术创新效率不确定性产生冲击作用，主要是由水平效应、规模效应和稳定性效应3个方面构成的。其中，规模效应和稳定性效应表现为非线性冲击作用，水平效应表现为线性冲击作用。

2.5 技术创新效率不确定性测度结果分析

2.5.1 不确定性变动信息的识别与获取

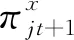
(11)

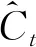
(12)

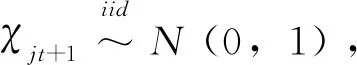
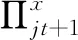
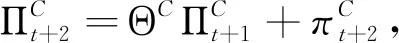
(13)

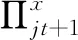
当l=3时，两个变量扰动项的FAVAR模型可表示为：

(14)

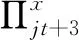
2.5.2 技术创新效率不确定性测度结果的构成

(15)

由向量自回归原理可知，在t时期变动到t+l时期后，技术创新效率xjt、共同因子Ct和不可观测变量At等3个变量形成新的自回归扰动项，其平方期望值等于各自方差期望值，即有：

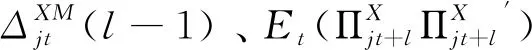
根据以上分析形成研究思路Ⅲ：当期技术创新效率变动和预测器对下期技术创新效率不确定性产生显著冲击效应。这种不确定性测度主要来自当期技术创新效率一阶自回归扰动项、预测器方差及其与技术创新效率协方差，技术创新效率随机变动方差是不确定性主要构成部分。

3 指标选择与数据处理

3.1 指标选择

技术创新效率不确定性变动是通过时期指标反映的，时期跨度为2002年1月至2017年12月，研究对象是沪深股市669家上市公司，分布在软件开发业、电气设备业、电子元器件业、汽车零部件业、通信设备业和医药生物业6个产业。指标来自于上市公司年度和半年度财务报表，分类情况说明如下。

(1)投入类指标，主要有R&D经费支出，无形资产摊销，购建无形资产支付的现金，处置无形资产的损失，R&D人员全时当量由其应付职工薪酬表示。

(2)产出类指标，包括每股收益、每股盈余公积、主营业务收入、上证加权平均市盈率、新产品总产值、新产品销售收入、新产品销售利润等。

(3)技术创新效率指标，反映上市公司技术创新活动投入产出比例，信息来源于投入和产出两个环节，包含有不可观测变量，随机因素较多，其变动是不确定性的。结合上市公司技术创新状况，实证分析中大量数据集合{Xit}包括的实证分析指标有7类，具体指标见表1。

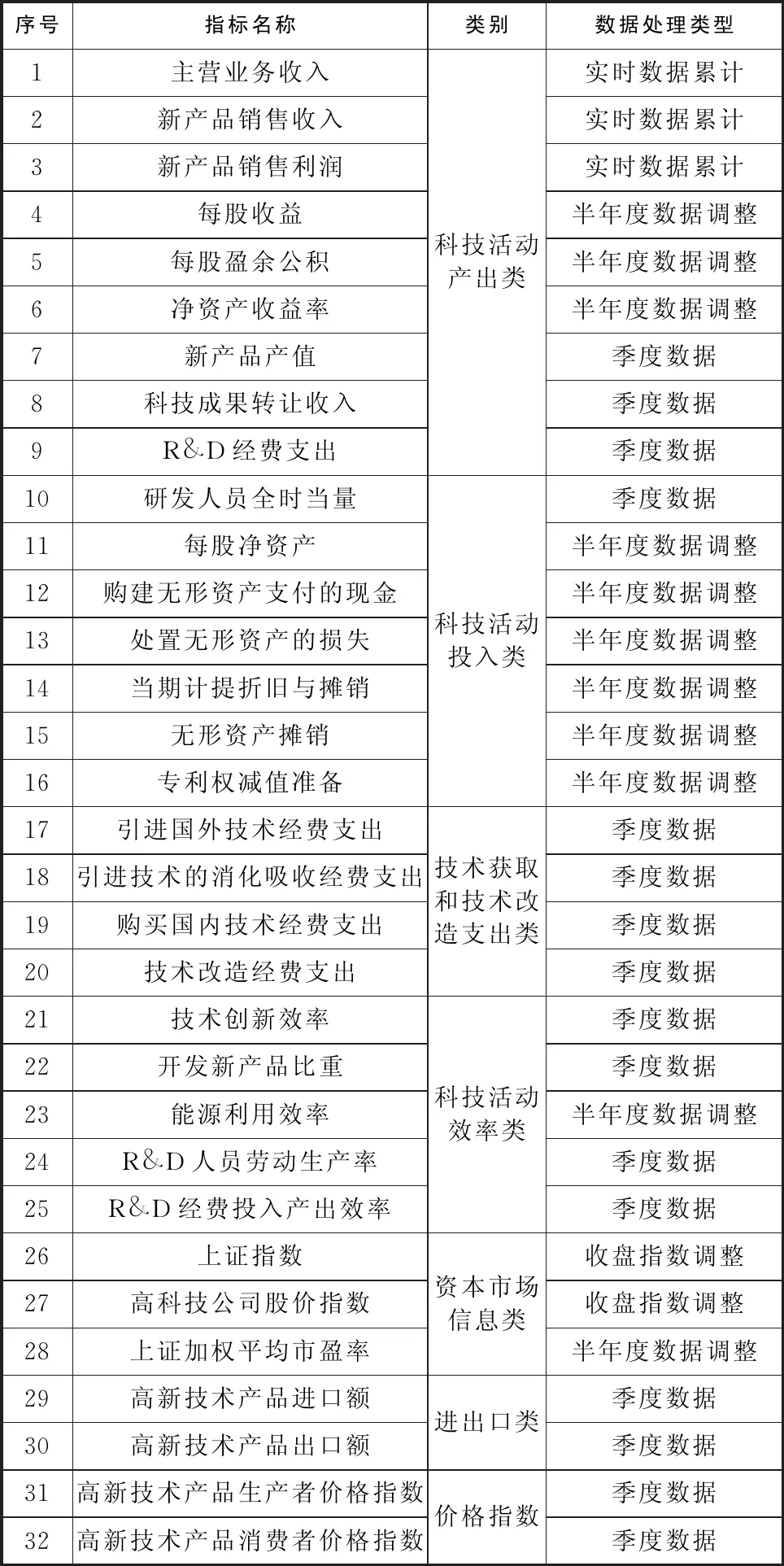
表1 上市公司技术创新活动大量数据集合的指标体系

3.2 数据处理

数据取自中国证券网上证报数据平台，实证分析利用国家统计局大中型工业企业行业数据和上市公司业绩预报等资料，对其半年报数据进行细化分解，获得相应的月度数据和季度数据。为消除可能存在的异方差，对数据进行一阶差分变换，把全部变量转变为平稳序列。本文研究的主要指标是技术创新效率不确定性程度，为使其包含更多信息量，对投入类和产出类指标分别进行去量纲化处理，再加权合并，综合反映技术创新效率变动情况，实证分析软件是Stata12.0。

4 实证结果分析

4.1 提取共同因子

根据研究思路Ⅰ，实证分析首先在大量数据集合中提取共同因子，充分挖掘既定变量所包含的技术信息，精准测度技术创新效率不确定性程度。通过运用主成分分析方法，从32个指标中提取7个共同因子，即R&D经费投入、研发人员全时当量、上证加权平均市盈率、新产品销售收入、新产品产值、主营业务收入、新产品销售利润。

主成分分析结果表明，第1个主成分对技术创新效率不确定性变动的解释程度达到0.6760，特征值和差异值分别为13.5202、11.5842，第2～7个主成分解释程度分别为0.0968、0.0524、0.0497、0.0405、0.0336、0.0185。7个主成分累计解释程度达0.9675，最大程度地包含技术创新效率不确定性变动信息。实证分析还显示出7个共同因子所对应的指标与特征向量，7个指标能够最大程度地覆盖技术创新活动投入产出信息。

4.2 技术创新效率不确定性比较分析

4.2.1 基于月度数据的技术创新效率不确定性比较分析

实证结果表明，技术创新效率不确定性程度在产出环节上，与新产品产值环比发展速度、前2期和前4期定基发展速度相关性不显著，相关系数仅为0.0045、-0.0019、0.0014，而主营业务收入、上证加权平均市盈率与之相关系数为0.0117、-0.0232、0.0448，0.0019、-0.0029、0.0792。9项相关系数的估计标准误分别是0.0619、0.2815、0.4721，0.0091、0.0061、0.0079，0.0024、0.0018、0.0025。由研究思路Ⅰ和Ⅱ可知，技术创新效率不确定性程度与产出指标相关性不显著，存在着不可观测变量。这种变动具有规模效应，逐步扩散放大，两者不是一维线性变动关系。

技术创新效率不确定性程度在要素投入环节中，与R&D经费投入环比发展速度、前2期和前4期定基发展速度的相关系数分别为0.0002、0.0020、 -0.0609，均低于主营业务收入和上证加权平均市盈率的回归系数0.0682、0.0917、0.6963，0.0011、0.0022、0.0316。相应的估计标准误分别为0.3935、0.4821、0.5019，0.0120、0.0075、0.0080，0.0043、0.0025、0.0023。技术创新效率不确定性程度在R&D经费投入中受到不可观测变量的冲击影响，连续作用于多个时期，而且具有一定的稳定性效应，存在着难以识别的技术信息，估计标准误处于较高水平，其不确定性程度波动起伏较大，具有明显的规模效应。

4.2.2 基于季度数据的技术创新效率不确定性比较分析

技术创新效率不确定性程度与新产品销售利润进行比较分析，技术创新效率不确定性程度在全样本、半样本时，一阶自回归系数为-0.1680、0.1928，而新产品销售利润一阶自回归系数为 -0.2709、-0.6734。相应的估计标准误分别为0.6106、0.7288，0.0153、0.0941。由研究思路Ⅰ和Ⅱ可知，技术创新效率不确定性程度一阶自回归系数明显低于新产品销售利润，而估计标准误又相对较高，不可观测变量较多，随机变动特征明显。另外，技术创新效率不确定性偏度峰度为-2.1709、12.1147，而新产品销售利润偏度峰度为0.7151、7.4593。技术创新效率不确定性偏度小于新产品销售利润偏度，而峰度又大于新产品销售利润峰度，其上下波动幅度明显大于后者，不确定性程度远远高于新产品销售利润。

技术创新效率不确定性程度主要取决于投入产出两个环节技术信息量，而新产品销售利润仅仅受到产出环节技术信息影响。两者分别与新产品产值环比发展速度、前2期和前4期定基发展速度回归系数分别为0.0001、0.0089、0.0136，0.2009、0.3842、0.5422，估计标准误分别为0.2946、0.4196、0.7182，0.0361、0.0530、0.0698。与R&D经费投入环比发展速度、前2期和前4期定基发展速度回归系数为-0.0036、0.0718、0.0830，0.0549、0.3086、0.5550，估计标准误为0.6685、0.8246、0.9261，0.0419、0.1545、0.1795。由研究思路Ⅱ可知，技术创新效率不确定性程度与两个变量3种不同发展速度之间回归系数相对较低，估计标准误又相对较高。技术创新效率中不完全技术信息较多，这种冲击作用在较短时期内是连续的，具有稳定性效应。受到大量不可观测变量的影响，其不确定性程度形成规模效应，得到快速扩散放大。

季度数据分析结果表明，技术创新效率不确定性程度、新产品销售利润分别与新产品产值、R&D经费投入环比发展速度回归系数，低于与前2期定基发展速度回归系数，与前2期定基发展速度回归系数又低于前4期定基发展速度。定基发展速度反映的时期越长，所体现的信息量越多，变量之间相关程度越高，回归系数越大，而所反映的时期越短，信息量越少，变量之间相关程度越低，回归系数越小。

4.2.3 基于半年度数据的技术创新效率不确定性比较分析

技术创新效率不确定性程度、新产品销售收入在全样本时一阶自回归系数为0.6478、0.7878，而在半样本时为0.3469、0.5584，估计标准误分别为0.6403、0.2026，0.7557、0.3296。技术创新效率不确定性程度一阶自回归系数均低于新产品销售收入，估计标准误高于新产品销售收入。技术创新效率不确定性自回归结果存在较大幅度波动起伏，受到不可观测变量的冲击较大，具有显著的随机变动特征。同时，技术创新效率不确定性偏度峰度分别为-0.4947、5.8691，新产品销售收入偏度峰度为1.5443、4.9288。由此可见，技术创新效率不确定性变动的偏度峰度存在较大落差，上下波动区间明显大于新产品销售收入。

技术创新效率不确定性程度、新产品销售收入与新产品产值环比发展速度、前2期和前4期定基发展速度的回归系数分别为0.0121、0.0127、0.0205，-0.0549、-0.0184、-0.0480，估计标准误分别为0.5084、0.6055、0.9105，0.0433、0.1379、0.1580。而与R&D经费投入环比发展速度、前2期和前4期定基发展速度回归系数分别为0.0225、0.0622、-0.0923，0.2098、0.4416、0.5155，估计标准误分别为0.5321、0.8347、0.9487，0.0839、0.1635、0.2005。根据研究思路Ⅱ可知，与新产品销售收入相比，技术创新效率不确定性程度对技术信息变动更加敏感，环比发展速度吸纳的信息量相对较少，对不确定性变动会形成稳定的冲击效应。而在前2期、前4期定基发展速度回归分析中，连续观察较长时期的产出水平变化，获取与利用的信息更多，具有更加显著的相关关系。

4.2.4 基于年度数据的技术创新效率不确定性比较分析

技术创新效率不确定性程度、新产品总产值全样本一阶自回归系数为-0.3687、0.4834，半样本为-0.7040、-0.9247，估计标准误分别为0.8597、0.5048，0.2881、0.0001。技术创新效率不确定性程度自回归系数仍然相对较低，波动起伏较大，估计标准误相对较高，两阶段技术信息得不到充分吸纳与传递。技术创新效率不确定性偏度峰度为0.1691、9.6857，而新产品产值偏度峰度为2.3856、7.9790。技术创新效率不确定性变动存在更多不完全技术信息，导致自相关系数相对较低，呈现出大幅度波动起伏变化。

技术创新效率不确定性程度、新产品产值分别与新产品产值环比发展速度、前2期和前4期定基发展速度回归系数分别为0.0068、0.0156、0.0300，0.0279、0.0488、0.0681，相应的估计标准误分别为0.3288、0.5074、0.7162，0.1448、0.2387、0.2849，两者对技术信息敏感程度具有较大差异。由研究思路Ⅱ可知，技术创新效率不确定性程度在投入产出环节中存在不可观测变量，难以充分识别技术信息，水平效应和稳定性效应不明显，规模效应相对显著，估计标准误较高。较小幅度的外生性因素冲击，带来明显的不确定性变化。技术创新效率不确定性程度、新产品产值与R&D经费投入环比发展速度、前2期和前4期定基发展速度的回归系数分别为0.0813、0.1399、0.1633，0.1733、0.2273、0.7163，估计标准误分别为0.3563、0.7357、0.9082，0.2634、0.6114、0.7011。技术创新效率不确定性程度与R&D经费投入3种不同发展速度的回归系数相对较低，而估计标准误又相对较高，受到大量干扰因素影响，投入信息没有得到充分吸纳。

4.3 基于投入产出环节的技术创新效率不确定性分析

技术创新效率不确定性程度分别与正增长、负增长的新产品产值、R&D经费投入开展回归分析。回归结果表明，技术创新效率不确定性程度与新产品产值发展速度的相关关系，没有随着新产品产值增长或下降而发生同方向变化。在1、5、6、7、8、9、10、12月份中，技术创新效率不确定性程度与全样本新产品产值之间相关系数分别为0.0071、0.0149、-0.0040、-0.0026、-0.0480、0.0605、0.0110、-0.0517，均处于与正增长和负增长新产品产值相关系数区间之外，技术创新效率不确定性具有随机变动特征。由研究思路Ⅱ可知，技术创新效率不确定性程度与新产品产值等产出指标关联程度较低，技术信息的水平效应和稳定性效应不显著，包含着大量不可观测变量。不完全技术信息得到扩散放大，对技术创新效率不确定性变动的冲击作用得到迅速扩散，产生规模效应，直接或间接地影响技术创新效率变动，识别这些因素可以更加精细地测度不确定性程度。

R&D经费投入出现正增长或负增长，并不一定带来技术创新效率相同方向变动，而是出现不确定性变动。实证结果分析表明，在3—11月的月度资料中，全样本技术创新效率与R&D经费投入的相关系数分别为0.0130、0.0620、0.0010、-0.0135、0.0198、0.0094、0.0003、-0.0060和-0.0544，偏离与R&D经费投入正增长和负增长相关系数。由研究思路Ⅱ可知，R&D经费投入作为共同因子，技术信息在冲击过程中没有出现显著的水平效应和稳定性效应，存在规模效应。技术创新效率不确定性程度没有随之增长而上升，也没有随之减少而下降，其变动趋势是不规则的。

4.4 技术创新效率不确定性程度的脉冲响应分析

4.4.1 变量选择

脉冲变量选择上市公司主营业务收入、研发人员全时当量、新产品销售利润等3个指标，响应变量选择t=1、6、12时期技术创新效率不确定性程度、上证加权平均市盈率和新产品产值等5个指标。首先分析时期长度h=6、12脉冲变量的单位方差变动对响应变量的方差贡献份额。根据方差贡献份额最大值及其所在的时期长度h，刻画响应变量的方差变动幅度与趋势，精准地测度技术创新效率不确定性程度。

4.4.2 选择主营业务收入作为脉冲变量

实证结果分析表明，脉冲变量在时期长度h=6、12时，t=1、6、12时期技术创新效率不确定性程度、上证加权平均市盈率等4个变量作为响应变量，相应的方差贡献份额分别为0.0138、0.0173、0.0509、0.0113，0.0933、0.1937、0.0200、0.0284，4个响应变量的最大方差贡献份额分别为0.0206、0.0120、0.2002、0.0301，对应的测度时期长度为41、41、37、50。与之相对应，新产品产值在这4次脉冲响应变动中，时期长度h=6、12时方差分别为0.2052、0.3305、0.2084、0.3249，0.2231、0.3421、0.1968、0.3349，4次响应变动的最大方差贡献份额为0.3464、0.3379、0.3604、0.3504，对应的测度时期长度为52、55、52、52。由研究思路Ⅱ和Ⅲ可知，t=1、6、12时期技术创新效率不确定性变动中包含有不可观测变量，导致随机变动特征明显，技术创新效率方差和一阶自回归扰动项是其不确定性变动的主要构成部分。不完全技术信息较多，受到主营业务收入等脉冲变量影响，不确定性变动形成明显的规模效应，在较短时期内出现大幅度波动变化。

4.4.3 选择研发人员全时当量作为脉冲变量

脉冲变量在时期长度h=6、12时，t=1，6，12时期技术创新效率、上证加权平均市盈率等4个变量作为响应变量，相应的方差贡献份额分别为0.0307、0.0508、0.0063、0.0075，0.0132、0.0186、0.0022、0.0024。4个响应变量的最大方差贡献份额分别为0.0511、0.0076、0.0224、0.0024，对应的时期长度为36、25、39、33，方差贡献份额在较短时期内出现较大变动。与之相对应，新产品产值在4次脉冲响应变动中，时期长度h=6、12时方差贡献份额分别为0.0719、0.0772、0.0678、0.0728，0.0809、0.0832、0.0711、0.0772，4次响应变动的最大方差贡献份额分别为0.0774、0.0735、0.0832、0.0777，对应的测度时期长度为47、46、42、49。根据研究思路Ⅲ可知，新产品产值作为共同因子，与上证加权平均市盈率构成预测器，技术创新效率与预测器协方差可以覆盖更多的技术信息，比较全面地反映技术创新效率动态变化情况，更加精准地测度其不确定性程度。

4.4.4 选择新产品销售利润作为脉冲变量

脉冲变量在时期长度h=6、12时，t=1，6，12时期技术创新效率不确定性程度、上证加权平均市盈率等4个变量作为响应变量，方差贡献份额分别为0.0187、0.0224、0.0061、0.0259，0.0666、0.1701、0.0165、0.0256，这4个响应变量最大方差贡献份额分别为0.0258、0.0265、0.1784、0.0264，对应的时期长度为47、41、41、57。由研究思路Ⅲ可知，新产品销售利润作为脉冲变量，预测器包含有市场结构、新产品价格、销售渠道等额外信息，预测器方差影响这种不确定性变动的趋势与幅度。而新产品产值在4次脉冲响应变动中，时期长度h=6、12时方差分别为0.1981、0.3316、0.2000、0.3281、0.2134、0.3394、0.1972、0.3434，4次响应变动中最大方差分别为0.3428、0.3369、0.3521、0.3508，对应的时期长度为55、49、47、22。变动幅度分布时期相对较长，具有显著的稳定性。

5 结论与政策建议

本文测度技术创新效率不确定性程度，运用主成分分析方法，在技术创新活动大量数据集合中提取共同因子，与其不能反映的不可观测变量构成预测器，建立因子增广向量自回归模型 (FAVAR)，充分挖掘既定变量的信息，有效利用现有数据资源，提高测度结果精准化水平，避免引入较多变量而导致信息叠加程度过高。实证分析以沪深股市软件开发业、电气设备业、电子元器件业、汽车零部件业、通信设备业和医药生物业6个产业669家上市公司技术创新效率为研究内容，在32个指标构成的多维数据集合中提取7个指标作为共同因子，获得最大化的技术信息量，使技术创新效率不确定性测度获得更多信息来源。

研究发现，FAVAR模型通过提炼共同因子，构建预测器，吸纳不可观测变量的大量信息，技术创新效率自回归扰动项变换为不确定性测度方差，正交化处理后即可获得不确定性测度结果。方差分解结果发现，一阶滞后因变量和预测器变动方差对技术创新效率不确定性测度结果形成3种冲击效应，即线性的水平效应和非线性的规模效应、稳定性效应，从而提高技术创新效率不确定性测度精准化水平。技术创新效率不确定性程度由4项构成，即技术创新效率自回归扰动项、预测器方差及其与技术创新效率协方差、技术创新效率随机变动方差。由此提出以下政策建议。

(1)坚持效率原则。合理选择创新要素投入时期，持续识别、吸纳与利用技术信息，避免不完全技术信息导致的资源错配和低效率利用，平缓技术创新效率随机变动幅度，坚持效率优先，大力提高要素利用集约化水平。

(2)优化要素配置。政府需要积极完善技术、信息等要素市场，最大限度地吸纳投入与产出环节中的技术信息，深度挖掘技术创新效率不确定性变动信息，准确识别与转化技术进步中随机因素，避免随机因素对技术创新效率的冲击，使其变动幅度控制在合理区间内。

(3)推进协同创新。以协同创新成果为支撑，使前后两期创新要素配置实现稳定运行，有效集成技术进步中知识、技能 、人才、信息等创新要素，降低不可观测变量在技术创新效率随机变动中的扩散效应，在成果引进、消化、吸收等各环节中积累更多水平效应，减少信息空档与断点。

(4)保持科技政策连续性。以稳定提高技术创新效率为目标，细化分析创新要素投入产出过程中各类政策性影响因素，突出技术进步不确定性变动的预测与研判，强化技术创新风险管控，减少不可观测因素的干扰，努力提高科技政策针对性和稳定性。