扇贝脱壳机特征值屈曲特性分析及优化

卢存壮， 张建华*， 王艾泉， 李府谦

(1.山东大学 机械工程学院， 山东 济南 250061；2.高效洁净机械制造教育部重点实验室/机械工程国家级实验教学示范中心， 山东 济南 250061；3.山东省机械设计研究院， 山东 济南 250031； 4.山东金瓢食品机械股份有限公司， 山东 威海 264300)

扇贝因肉质鲜嫩、营养丰富而深受消费者的喜爱和追捧[1]。实现扇贝闭壳肌与壳体分离是扇贝加工的关键环节之一[2-3]。河北农业大学谷晓翠[4]开发出一种转盘式闭壳肌剥离生产线，以凸轮分割器作为传动机构，实现扇贝壳肉分离要求；尹欣玲等[5]设计出一种成形刀撑开式工作台，实现闭壳肌脱离贝壳表面；解秋阳等[6]利用水射流数控装置使闭壳肌脱落；朱其霄[7]通过对扇贝生物结合力的测量，研制出一种外套膜剥离机械手。张建华、王艾泉和李府谦共同提出并研发一种扇贝脱壳机，对蒸煮后的扇贝进行脱壳处理，从而实现扇贝闭壳肌与壳体的分离。

课题组基于SolidWorks建立扇贝脱壳机实体模型后，利用ANSYS Workbench 18.0对脱壳机进行屈曲分析，通过变密度法进行拓扑优化设计，以减轻结构质量，将优化前后模型的屈曲分析结果分别进行了对比，以保证优化后的结构仍满足实际工况要求。

1 扇贝脱壳机三维模型的建立

课题组采用SolidWorks建立三维实体模型，如图1所示，并将模型文件导入ANSYS Workbench中。

图1 扇贝脱壳机三维模型Figure 1 Three-dimensional model of scallop sheller

2 有限元分析

2.1 建立有限元模型

在Eigenvalue Buckling屈曲分析模块中，脱壳机材料定义及性能参数如表1所示。有限元分析过程中，模型结构与网格划分的方法影响划分网格的质量和速度[8]，基于上述问题，课题组采用正四面体划分网格，共划分成115 297个单元和275 973个节点。忽略螺栓、螺母等特征，假定所有焊接接头都为完全焊接进行有限元模型简化，如图2所示。

图2 简化后的有限元模型Figure 2 Simplified finite element model

2.2 施加约束及其载荷

根据实际工况，将脱壳机机架的8个支腿施加固定约束；每个电机板施加Z轴负方向500 N的力；每层筛网施加Z轴负方向400 N的力；Z轴负方向翻拨轮自身的重力为300 N。各处力施加完成后如图3所示。

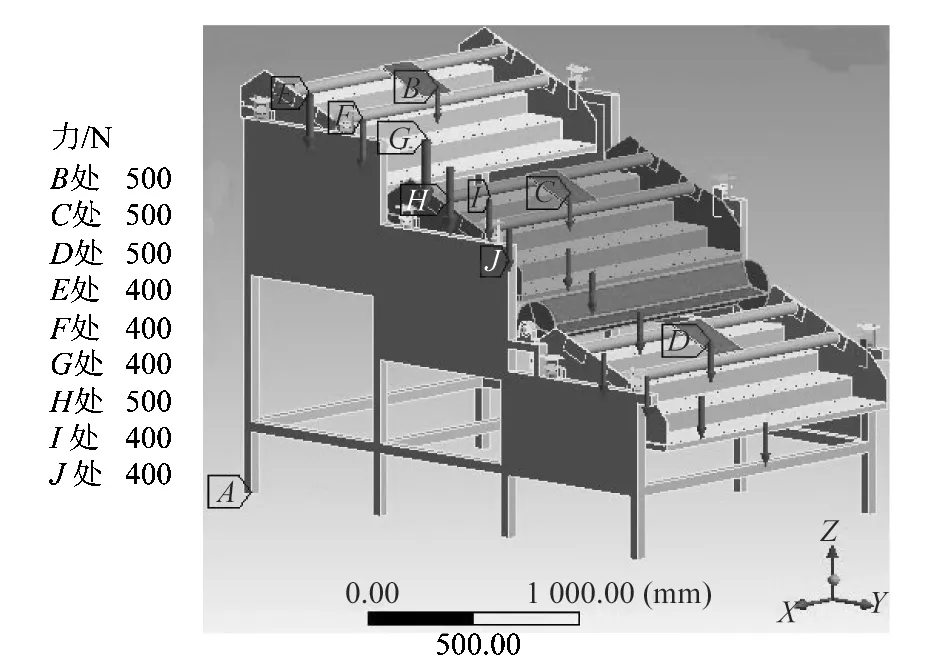
图3 扇贝脱壳机约束及载荷的施加Figure 3 Scallop sheller restraint and load application

3 屈曲分析

3.1 屈曲分析理论

屈曲分析是研究结构受到外力作用下发生失稳状态时，结构产生屈曲特征值和模态形状的分析方法[9-11]。课题组采用线性屈曲对脱壳机进行稳定性分析。线性屈曲是以小位移、小应变的弹性力学为基础，分析时不考虑结构在受载时发生的变化[12-15]。

发生屈曲时，临界载荷为[16-18]

Fcr=λ·F。

(1)

式中：Fcr为临界载荷,N；F为作用载荷,N；λ为屈曲特征值或屈曲载荷因子。

其中，λ的计算方程为

([K]+λ[S]){Ψ}=0。

(2)

式中：[K]为脱壳机的刚度矩阵；[S]为脱壳机的应力刚度矩阵；Ψ为脱壳机的位移特征矢量。

3.2 屈曲分析结果

利用Block Lanczos法求解脱壳机前6阶屈曲特征值，如表2所示。

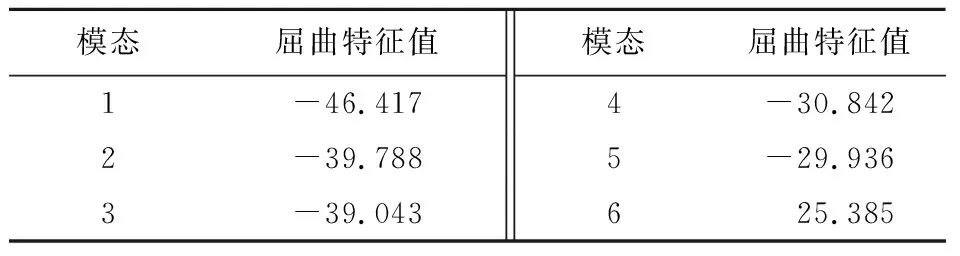
表2 屈曲特征值Table 2 Buckling eigenvalue

得到的屈曲特征值既可以是正值也可是负值，负值表示施加相反方向载荷时结构发生的破坏。屈曲特征值大于1表明施加载荷未超过临界载荷值，结构整体满足稳定性要求；反之，结构发生失稳[19]。从表2可知，脱壳机满足设计要求，未发生失稳。

基于发生1阶屈曲变形时的临界载荷最小且1阶振型表示结构首次发生屈曲失稳的位置，特征值和模态振型应以1阶为主，如图4所示。

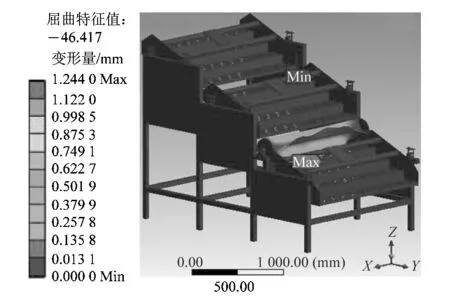
图4 1阶屈曲振型Figure 4 First-order buckling mode

模态振型可以用来预测脱壳机发生失稳时的特征。通过图4屈曲振型可以看出，屈曲振型主要表现为局部弯曲，变形以局部失稳为主，翻拨轮的上边缘是发生变形的主要位置。如果脱壳机在该位置处存在焊接工艺不符合设计规范及表面有缺陷裂纹等问题，屈曲载荷值会受到直接影响，结构稳定性也会降低。

经有限元屈曲稳定性计算，1阶屈曲特征值为46.417，则1阶屈曲载荷为实际载荷的46.417倍，在相应载荷作用下满足屈曲稳定性要求，脱壳机整体结构是安全的。根据材料力学相关知识[20]，失稳时的临界载荷等于施加的载荷与屈曲特征值的乘积。

4 拓扑优化分析

4.1 拓扑优化分析理论

由屈曲分析结果可知，脱壳机机架结构留有较大的优化空间。将模型导入Topology Optimization模块中，采用变密度法数学模型进行拓扑优化以实现轻量化目标[21-22]。

针对上述优化方案的要求，以质量最小为优化目标函数，屈曲特征值为约束条件进行连续体结构的拓扑优化，数学模型可由式(3)～(5)表达。

Find：ρ={ρ1，ρ2，ρ3，…，ρn}∈Ω。

(3)

(4)

(5)

式中：Ω为整个结构的设计区域，ρ为设计变量，ρi为相对密度，vi为相对体积，m为目标函数，即脱壳机质量，Umax为最大屈曲特征值。

4.2 拓扑优化结果分析

在Topology Optimization模块中材料属性、约束条件与负载的设置和屈曲分析相同。优化区域设定为机架；优化目标设定为去除25%的材料，设定完成后进行拓扑分析。

优化结果如图5所示。优化后的模型导入Eigenvalue Buckling模块中，求解屈曲特征值和1阶屈曲振型，结果分别如表3和图6所示。

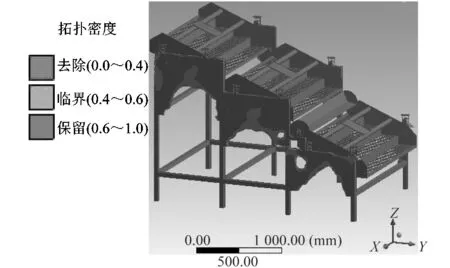
图5 拓扑优化结果Figure 5 Topology optimization results

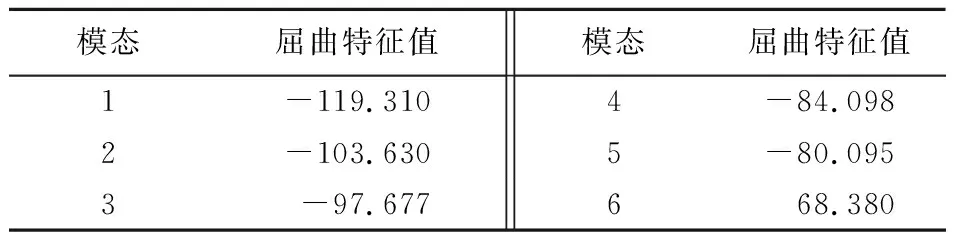
表3 拓扑优化后的屈曲特征值Table 3 Buckling eigenvalues after topology optimization

图6 拓扑优化后的1阶屈曲振型Figure 6 First-order buckling mode shape after topology optimization

根据拓扑优化结果，与脱壳机优化前的参数对比，如表4所示。由表4可知，脱壳机整体质量减轻了12.5%，最大变形量由1.244 mm增加到1.249 mm，增加0.4%，在合理变化范围内。拓扑优化后，屈曲特征值由未优化前的-46.417增加到-119.31，增加显著，拓扑优化后的脱壳机稳定性并未降低，仍能满足正常工况需求。

表4 脱壳机拓扑优化分析结果对比Table 4 Comparison of topology optimization analysis results of sheller

5 结论

1) 课题组以扇贝脱壳机为研究对象，以屈曲分析为理论基础，运用有限元分析软件ANSYS Workbench中的Eigenvalue Buckling模块，得到了脱壳机在实际工况下的屈曲特征值和模态振型。仿真结果表明，该脱壳机屈曲特征值为46.417，脱壳机整体稳定性符合使用要求，即脱壳机在实际载荷下，不会发生整体失稳。

2) 课题组利用Topology Optimization模块对脱壳机进行拓扑优化，实现轻量化目标。经过拓扑优化后，脱壳机质量减轻了12.5%，但屈曲特征值并未减小，说明优化后的脱壳机仍能满足实际工况下的载荷。该方法为脱壳机的后续实际加工生产提供了一定的参考价值。