基于TMS320F28379D和Σ-Δ调制的旋变软件解算系统

王 迪， 马钧华

(浙江大学 电气工程学院， 浙江 杭州 310027)

伺服系统是用来精确跟随或复现目标过程的反馈控制系统，主要包括伺服控制算法、功率驱动、信号检测和伺服电机4个模块[1]。磁场定向以其优越控制性能广泛应用于交流伺服系统。磁场定向控制通过采样交流伺服系统三相电流并对其进行基于转子磁链角度的数学变换得到解耦的电流量，再根据电流解耦量、控制量和转子位置角进行动态调节，控制交流伺服系统工作在最大转矩电流比状态[2]。转子位置角主要用于位置闭环控制和转子磁场定位的解耦，因此其精度在一定程度上决定了磁场定向控制的控制性能。

课题组搭建了基于TMS320F28379D的交流伺服控制平台，转子位置角由同轴连接的旋转变压器提供。功率模块使用变频器的主回路部分，其通过接口实现与DSP的PWM信号、电压电流检测信号传递。

旋变信号需要解码才能利用。专用旋变数字转换器如AU6805、AD2S1210等集旋变激励、信号采样、位置解码和数据通信等功能于一体，但需要额外的信号隔离，且成本较高。此外，解码输出还需要通过SPI通信、编码器模拟信号ABI或并行接口与控制DSP对接，存在二次延时的问题。最新的特斯拉Model3电动汽车控制板也使用DSP软解码而放弃了专用解码芯片。

课题组利用低成本的HCPL-7860芯片实现旋变信号的Sigma-Delta(Σ-Δ)采样，并设计了基于锁相环原理的数字R/D转换电路以实现旋变软解码。在保证位置解码精度的基础上简化电路结构、降低延时并降低成本。

1 旋转变压器

旋转变压器由采用无刷结构的定子绕组和转子绕组构成，其中定子绕组由励磁绕组和2个空间位置相差90°的输出绕组构成[3]。旋转变压器的基本结构如图1所示。

旋变励磁绕组接收正弦激励ER1-R2，其转子绕组感应出同频的恒幅正弦信号。转子旋转使得旋变的定转子绕组相对位置角发生改变，定子正交绕组感应出按转子位置角的正余弦规律变化的同频调制波。

定子侧励磁绕组的正弦激励为

ER1-R2=Esin (2πft)。

(1)

则定子侧正交绕组的输出信号为：

(2)

式中：f为旋变激励信号频率，实验中取10 kHz；E为激励信号幅值；K为变压器变比；θ为转子位置角。

旋变反馈的调制波信号包含了转子位置角信息，通过反正切函数即可求得[4]：

θ=arctan (ES1-S3/ES2-S4)。

(3)

2 Sigma-Delta(Σ-Δ)采样

ADC作为常用模数转换方式，其采样精度高，转换速度快，但抗干扰能力差且信噪比低。Σ-Δ采样无需外围采样和保持电路，且可以在采样过程中通过噪声量化整形与抽取滤波实现高频噪声的抑制。这是Σ-Δ采样相比于ADC的优势所在[5-6]。

2.1 硬件电路设计

旋变信号Σ-Δ采样电路结构如图2所示。TMS320F28379D产生的旋变激励信号经放大电路处理后对旋变进行励磁。旋变反馈信号经Σ-Δ采样电路调制为数据信号MDAT与时钟信号MCLK。DSP的SDFM模块对调制信号进行滤波和降采样处理得到旋变反馈信号的采样值。采样值经后续解码算法处理得到转子位置角，以供磁场定向控制使用。

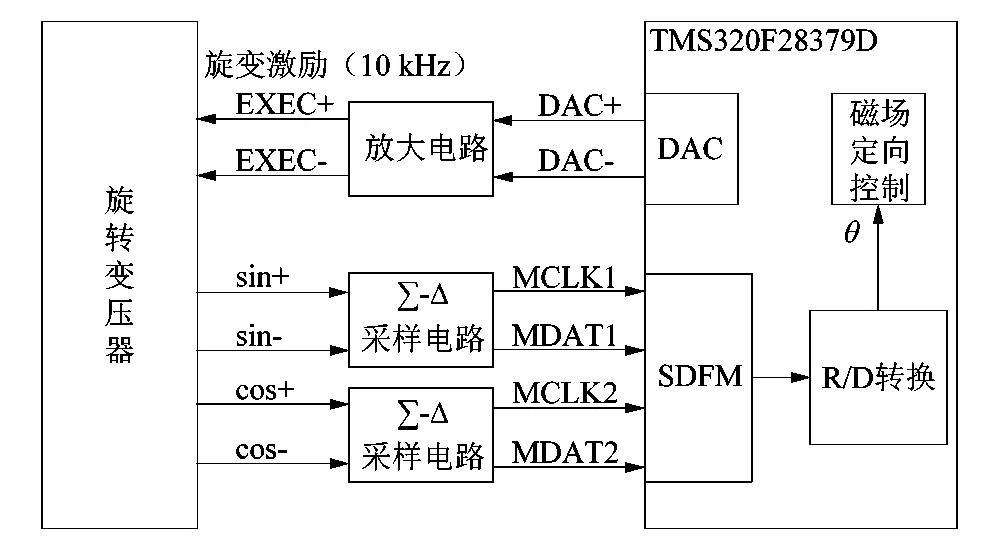
图2 Σ-Δ采样电路结构Figure 2 Σ-Δ sampling circuit structure

DAC模块输出的差分信号驱动能力不足，需经放大电路进行驱动能力增强处理才能对旋变进行励磁。差分信号DAC+和DAC-两者放大电路相同。旋变激励信号(DAC+)放大电路如图3所示。

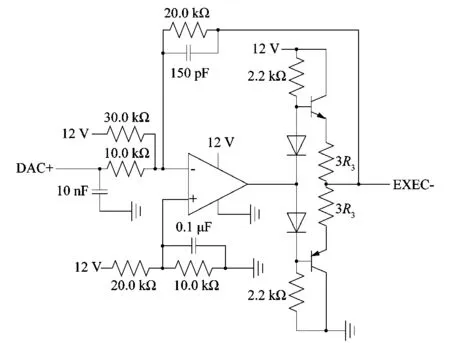
图3 激励信号放大电路Figure 3 Excitation signal amplifier circuit

分析图3电路结构可得：

VEXEC+=2×(3.3-VDAC+)。

(4)

VDAC+的电压范围为0.0～3.3 V，推算得到VEXEC+的电压范围为0.0～6.6 V。激励信号经放大电路处理，其偏置电压与幅值均放大2倍。正极性的VEXEC+与负极性的VEXEC-，按差分输出VEXEC+-VEXEC-作为旋变的激励。

Σ-Δ采样电路如图4所示，ES1-S3与ES2-S4的采样电路相同。

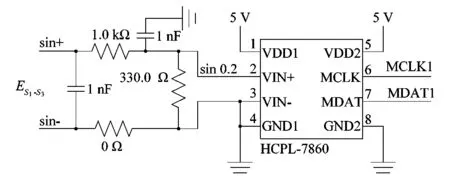
图4 Σ-Δ采样电路Figure 4 Σ-Δ sampling circuit

HCPL-7860芯片是一款精度达12 bit的Σ-Δ采样芯片，主要实现Σ-Δ采样和信号隔离功能。芯片内部时钟频率为10 MHz，其输出时钟与数据信号频率也为10 MHz。本实验采用共地的接法，可根据需要设计为原/副边隔离的用法。

实验中旋变反馈差分信号ES1-S3的最大峰峰值为1.4 V，经前置电路滤波分压后的信号Sin 0.2的峰峰值为347 mV，满足HCPL-7860最大输入端±200 mV的量程。

2.2 Sigma-Delta(Σ-Δ)采样原理

Σ-Δ采样原理如图5所示，主要分为调制(7860芯片)和解调(DSP的SDFM模块)2大模块。图5(c)中各采样点在时间轴上均匀分布。

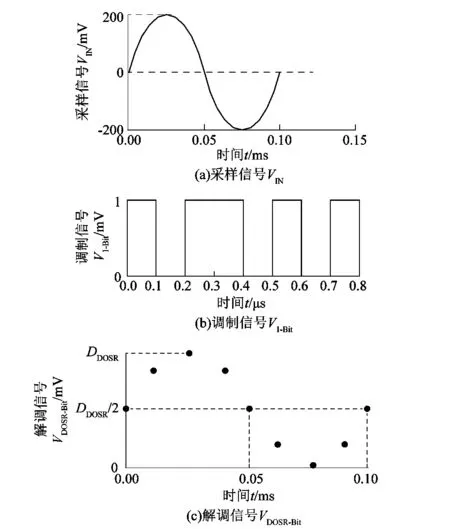
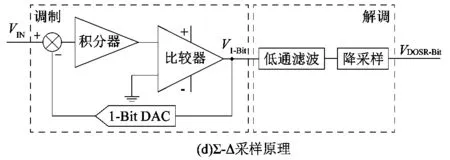
图5 Σ-Δ采样原理Figure 5 Σ-Δ sampling principle

Σ-Δ采样调制模块将10 kHz的旋变反馈信号VIN调制为10 MHz的1bit数据流V1-bit。调制模块输出信号V1-bit的过采样率为1 000。数据流V1-bit的单个比特信号包含被采样信号相邻时刻的信号差信息。V1-bit的脉冲密度包含了被采样信号的绝对值信息，脉冲密度是指单位时间内高电平信号的比例。若VIN接近0，其脉冲密度接近50%；若VIN接近正量程，其脉冲密度接近100%；若VIN接近负量程，其脉冲密度接近0%[7]。

Σ-Δ采样解调模块对数据流V1-bit进行低通滤波和降采样处理。旋变反馈信号经Σ-Δ调制，其噪声被整合到高频段(噪声量化整形)。利用解调模块的低通滤波器将高频噪声除去，可以提高采样值的信噪比。降采样处理是指计算V1-bit中一定数量比特信号的脉冲密度，而被统计的比特信号数量称为降采样率DDOSR。过采样率为1 000的V1-bit经降采样处理，得到过采样率为1 000/DDOSR的采样信号VDOSR-bit。

本实验设定Σ-Δ采样的过采样率为16。

3 旋变信号解码算法

伺服系统匀速运行时，旋变反馈信号如图6所示。

图6 旋转变压器一个周期反馈信号Figure 6 Feedback signal of rotary transformer of one cycle

3.1 开环解码-反正切法

反正切法是一种对旋变反馈信号采样值进行反正切计算的开环位置解码算法，其具有延迟低的特点。频率达200 MHz的高计算性能28379D芯片内置了TMU三角函数模块，可以实现反正切法的快速计算。

10 kHz单位激磁周期的旋变反馈信号经Σ-Δ采样得到16个采样点。旋变反馈信号采样值如图7所示，图中一个周期为一个激磁周期(0.1 ms)。

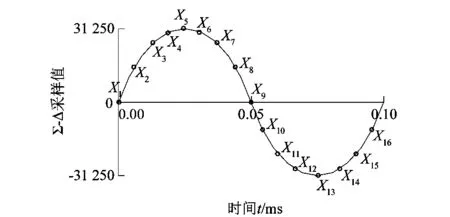
图7 单位激磁周期采样点Figure 7 Sampling point of unit excitation period

对单点采样值进行反正切法解算会在信号过零点位置产生计算误差，故本实验先求取旋变反馈信号的包络线再进行反正切计算[8]。反馈信号的包络线可以通过计算单位激磁周期信号的幅值与极性来获取。

实验中利用离散傅里叶变换对16个采样值进行处理得到被采样信号的基波幅值与极性。此方法无视直流偏置的影响，并可以除去基波以外的高次谐波。

运用离散傅里叶变换求取旋变信号包络线需要完整激磁周期的采样值，存在一定延时。故可以对采样信号进行相敏整流并剔除干扰的采样值，通过计算半个激磁周期面积或者使用窗函数截断法对其实现更高过采样率计算。

根据2路调制信号包络线即可用反正切法计算出转子位置角。

3.2 闭环解码-锁相环法

3.2.1 解码原理

反正切法作为一种开环解码算法，易受噪声干扰且解算值波动较大。基于锁相环原理的R/D转换模块可以提高解算系统的抗干扰能力，且能准确跟踪转子角速度和位置角信息。专用旋变转换芯片AD2S1210也采用了R/D转换模块进行位置解码。

基于锁相环原理的R/D转换模块结构[9]如图8所示。

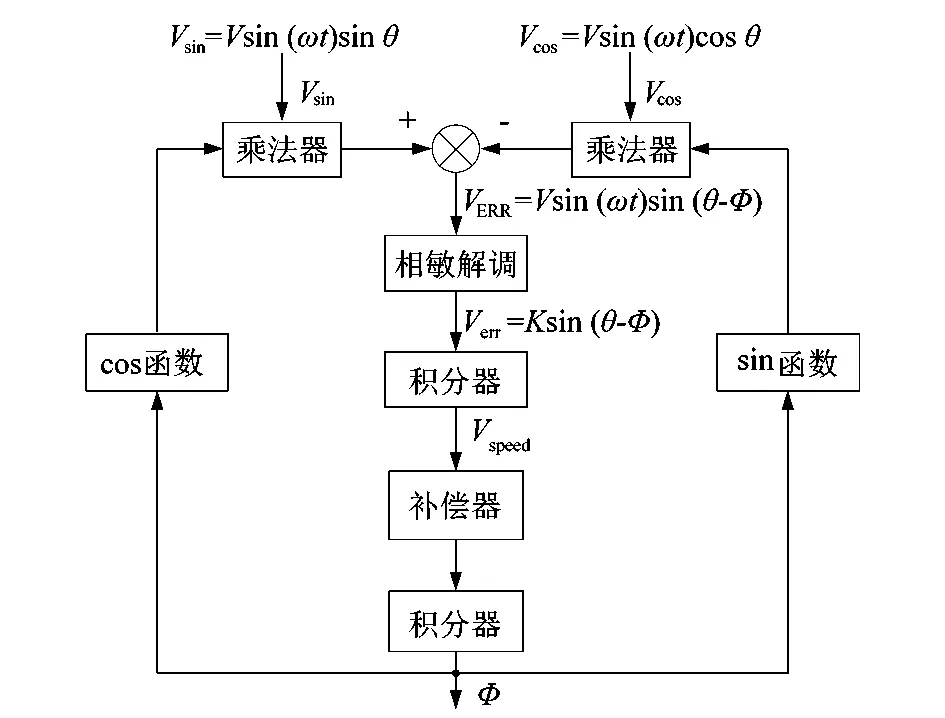
图8 R/D转换模块结构Figure 8 R/D transformation module structure

旋变反馈信号采样值Vsin与Vcos分别与锁相环输出转子位置角估计值Φ的余弦值cosΦ和正弦值sinΦ相乘，得到与激磁信号sinωt耦合的误差信号VERR。VERR经过相敏解调得到解耦的误差信号Verr。

相敏解调分为相敏整流和低通滤波2部分。硬件电路采用的相敏整流法为将误差信号VERR与激磁信号sinωt相乘，得到误差信号Verr与激磁信号2倍频的叠加值。2倍频激磁信号由低通滤波器除去[10]。

误差信号Verr包含转子角加速度信息，经过积分得到转子速度信号Vspeed，转子速度信号经过积分得到累加的转子位置角[11]。补偿器起超前校正的作用，改善闭环传递函数的滞后性。

3.2.1 实验算法

参考AD2S1210的硬件电路结构在DSP中构造数字R/D转换算法[12]。算法过程如图9所示。

图9 数字R/D转换电路Figure 9 Digital R/D conversion circuit

算法中对耦合的误差信号VERR使用方波信号进行相敏整流，并设计了一个通带截止频率为2 kHz，阻带截止频率为20 kHz的FIR数字低通滤波器进行滤波。

FIR数字低通滤波器参数如表1所示。

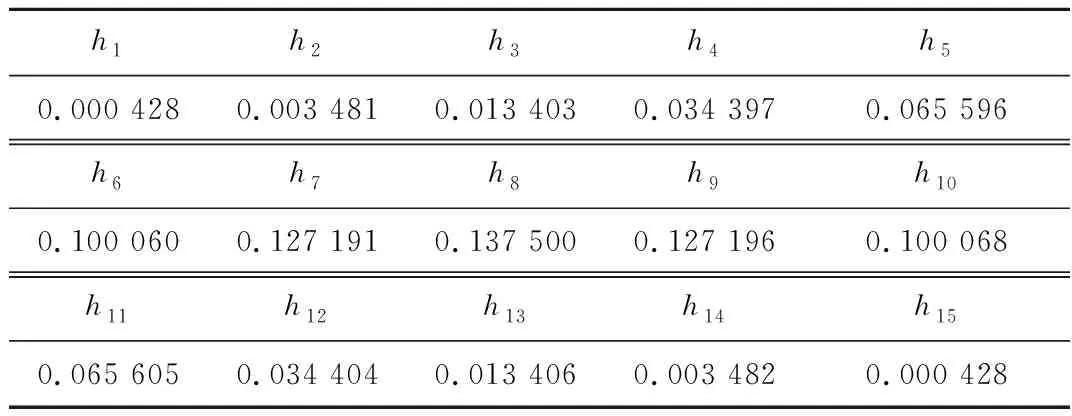
表1 FIR数字低通滤波器Table 1 FIR digital low pass filter

相敏解调过程:

(5)

式中：n=N代表前第N个采样时刻，n=0代表当前采样时刻；Pn为方波相敏整流系数。

R/D转换电路开环传递函数为：

(6)

将G(z)转换到S平面得开环传递函数:

(7)

其中：

实验中根据开环传递函数设计了2套解码精度不同的数字R/D转换系统，其参数设置如表2所示。

表2 数字R/D转换系统参数Table 2 Digital R/D conversion system parameters

对由系统Ⅰ和系统Ⅱ参数构建的R/D转换系统进行相频特性分析，结果如图10所示。

图10 系统相频特性Figure 10 System phase frequency characteristics

相比于系统Ⅱ，系统Ⅰ的开环直流增益Ka较大，其解算精度较低。但系统Ⅰ的带宽更宽，同等频率下系统Ⅰ的相位滞后更小。

4 实验数据

4.1 ADC与Σ-Δ采样精度对比

实验中分别采用ADC与Σ-Δ对旋变反馈信号进行16倍过采样，位置角解码算法均选择反正切开环解码算法。考虑到Σ-Δ采样过程中数字滤波环节SINC滤波器的阶数对采样精度存在一定影响，故Σ-Δ采样滤波部分分别采用1阶、2阶、快速2阶与3阶低通滤波器进行对比测试。记录伺服系统静止状态下200个位置解码值，统计分析其标准偏差与最大偏差(最大值与最小值之差)。

不同采样方式的采样精度如表3所示。

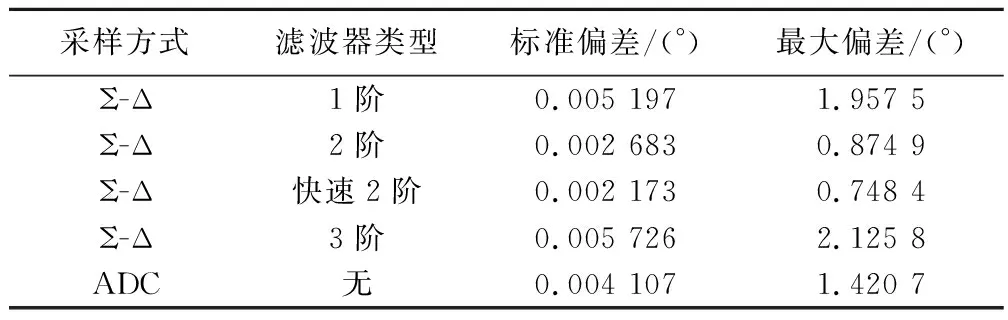
表3 不同采样的采样精度Table 3 Sampling accuracy of different samples

由表3分析可得，使用快速2阶低通滤波器的Σ-Δ采样的精度高于ADC采样。

4.2 闭环解码算法性能分析

测试闭环解算系统的性能，以开环解算系统作为对照组。实验中采样方式均选择Σ-Δ采样，分别使用开环反正切法和闭环锁相环法对采样值进行解码运算。其中闭环锁相环法分别使用表2中系统Ⅰ和Ⅱ的参数构造的2种数字R/D转换电路。

对比分析开环解码算法与闭环解码算法的解码精度。记录伺服系统静止状态下200个位置解码值，统计分析其偏离均值的误差。

静止状态测试结果如图11所示。

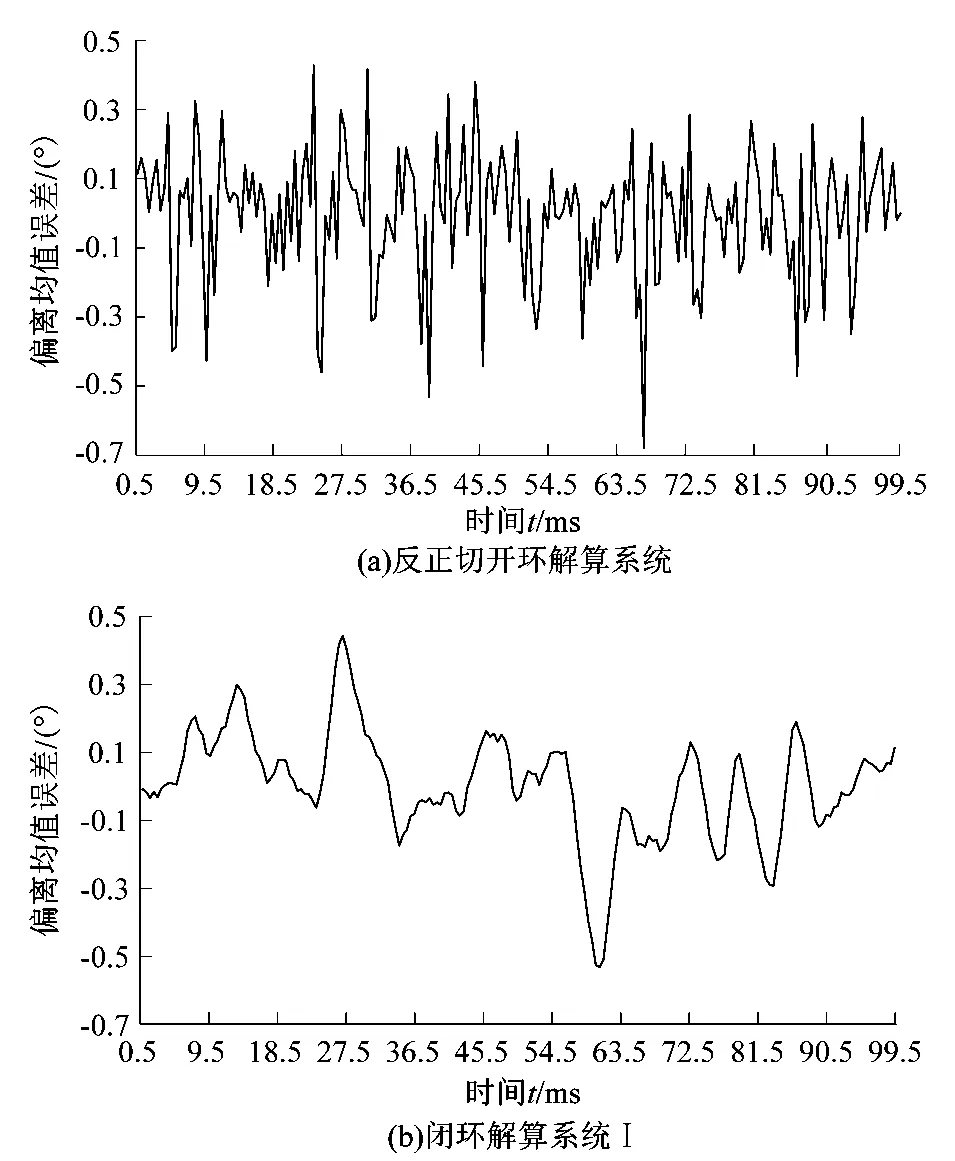
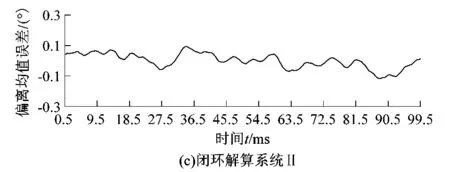
图11 转子位置角解算精度Figure 11 Rotor position angle calculation accuracy

由图11分析可得，基于锁相环原理的闭环解算系统的解码精度高于开环解算系统，且闭环解算系统使转子解算值变化较为平缓。闭环解算系统Ⅰ的解算精度低于系统Ⅱ的解算精度，与理论设计精度相符合。

使伺服系统运行在不同速度状态下，对比分析2种精度闭环解算系统的跟踪误差(以低延迟的开环解算系统为参考)。动态状态下转子位置角延时误差如图12所示。图中低于转折点速度使用解算系统Ⅱ，高于转折点速度使用系统Ⅰ。

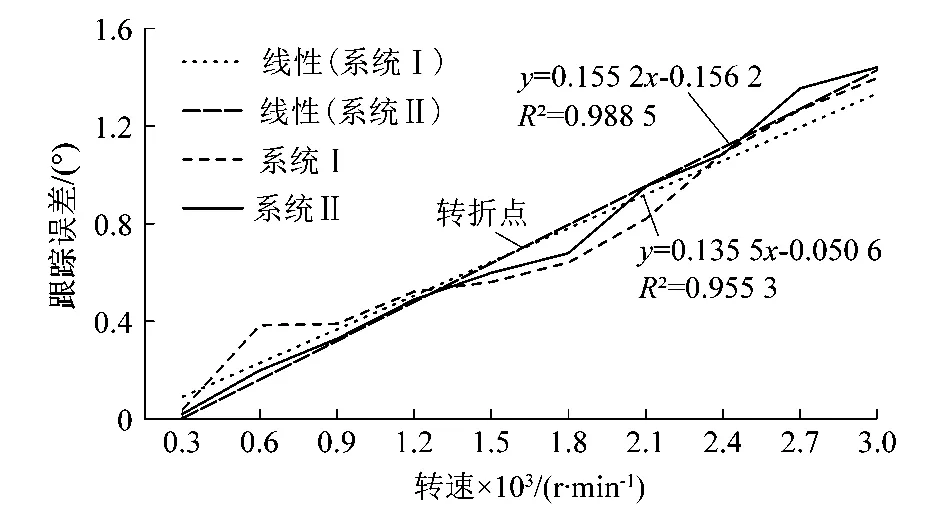
图12 转子位置角延时误差Figure 12 Rotor position angular delay error

分析可得，转子位置角闭环解算系统的相位延迟使转子跟踪误差随伺服系统转速增加而增大。实验发现，电机处于低速状态时，使用闭环解算系统Ⅱ造成的转子跟踪误差更小；电机处于高速状态时，使用闭环解算系统Ⅰ造成的转子跟踪误差更小。可以根据速度切换不同精度闭环解算系统以获得误差最小的转子位置估计值。

5 结语

课题组通过实验验证了Σ-Δ采样可以通过噪声量化整形实现高于ADC的信号采样精度。基于锁相环原理的双精度数字R/D转换电路可根据速度量的检测值切换不同精度解码系统，以实现高跟踪精度转子位置角估计。由于转子位置估计值总是会落后于转子位置实际值，因此电机在高速运行时产生的延时误差还可以通过转速积分进行角度补偿来解决。