波纹节距对板壳式换热器壳程流动性能和阻力性能的影响

石迎迎， 赵 巍*， 袁雨文， 张 华， 潘书毅， 袁兴阳

(1.上海理工大学 能源与动力工程学院， 上海 200093； 2.上海市质量监督检验技术研究院， 上海 201114)

板壳式换热器是一种高效换热设备，广泛应用于诸如石油化工和能源电力等领域[1]。导孔型板壳式换热器作为板壳式换热器的一种，结构更加紧凑、占地面积更小，它的应用更为普遍。

陈武斌等[2]发现一种蜂窝结构板片的板壳式换热器，并发现蜂窝间距、蜂窝高度及焊点排布会对传热与阻力的性能产生影响。栾辉宝[3]从实验和模拟两个方面对导孔型板壳式换热器进行了研究，得出壳程内孔的存在使壳侧流体温度发生较大的变化。刘家瑞[4-5]针对板壳式换热器壳侧流体分布不均问题提出设置圆形封头和圆弧状波纹板来有效解决流量分配问题。徐辉[6]对板管型板壳式换热器的两侧进行模拟，得出壳程进出口处的速度变化剧烈，流量分布均匀性较差。袁雨文[7-9]发现人字形波纹板壳式换热器板侧波纹角度对导孔型板壳式换热器的壳程换热有较大影响。

板壳式换热器壳侧流体对换热器的流动性能有较大影响，学者们对板壳式换热器研究虽多，但对人字形波纹板片的板壳式换热器壳侧有较大影响的波纹节距、波纹高度和波纹角度研究不够充分。为深入了解波纹节距对板壳式换热器壳侧流动性能的影响，课题组建立单流道三维物理模型，对板壳式换热器壳程流体的流动性能和阻力性能进行数值模拟研究。

1 数值模拟计算模型

1.1 物理模型

课题组参考广东某换热器生产商所提供的APS46型全焊接[10]人字形板壳式换热器板片[11]，对其主流区进行几何建模，如图1所示。流体通道如图2所示，板片主流区外形尺寸见表1。

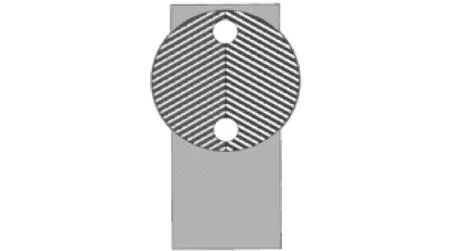
图1 物理模型Figure 1 Physical model

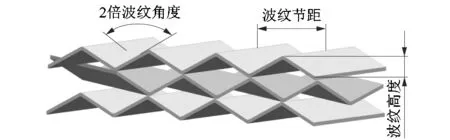
图2 流体通道结构图Figure 2 Fluid channel structure diagram

表1 波纹节距的几何参数表Table 1 Geometric parameter table of corrugated pitch

1.2 数学模拟

本课题研究的是单相对流换热问题，满足连续性方程、动量方程和能量方程，采用湍流模型为RNGκ-ε模型[12]。结合板壳式换热器的流动和换热的特点，假设壳程流体为不可压缩的常物性流体，流体的流动为三维稳态单相对流换热，同时忽略浮升力和重力以及流体流动过程中的黏性耗散[13]。计算传热控制方程如下：

1) 连续性方程

2) 动量方程

3) 能量方程

式中：ρ为流体密度，kg/m3；μ为动力黏度，kg/(m·s-1)；u，v和w为流体分别在x，y和z方向的流速，m/s；t为时间，s；Su,Sv,Sw为动量方程的广义源项；λ为导热系数，W/(m·K)；cp为比热容，J/(kg·K)；ST为所有体积内热源。

1.3 网格划分和无关性验证

模型在几何结构、荷载和换热等条件下具有对称分布特性，因此选用具有对称性的半个实体进行非结构化网格划分。通过努塞尔数和压降的变化来判断网格无关性影响。如图3所示，随着网格数量的增大，平均努塞尔数逐渐增大直至趋于平稳，压降先增大后减小最后趋于稳定；当网格数量达到700万之后努塞尔数和压降的变化趋势不明显，此时网格数量对结果不再产生影响，保证了模拟结果的准确性[14]。因此选用网格数量为700万左右，整体网格及局部网格放大显示如图4和图5所示。

图3 网格无关性检验Figure 3 Grid independence test

图4 整体网格Figure 4 Overall grid diagram

图5 局部网格Figure 5 Local grid diagram

1.4 边界条件

壳程工质为水，定义入口为速度入口边界，入口温度为323 K；流道出口为压力出口，压力为101.325 kPa；定义上下波纹板片壁面为恒温壁面，壁面温度为300 K；剩余壁面设置为不可渗透，无滑移绝热边界条件[15]。

应用控制容积法及非耦合稳态隐式格式求解控制方程组，压力和速度选择传统的SMPLE方法，离散化为二阶精度的迎风模式进行运算[16]。

2 数值模拟计算分析

2.1 不同波纹节距的流动性能

由图6可以清楚地看到流体在壳程的流动情况：流体的流向为从左至右，在流道的左侧入口处，由于受到角孔的阻碍，流线向两侧发展，直至绕过角孔后重新会合。当波纹节距P小于7.9 mm时，流体的流动以十字交叉状为主，十字交叉流的比例明显高于曲折流；当P为7.9 mm时，曲折流比例升高，十字交叉流比例下降[17]；而当P增大至9.9 mm以上时流态基本为纯曲折流。这一现象的出现是因为随着波纹节距增大，触点数目直线下降，波纹陡度逐渐变缓，流向更易受对侧流体的拖拽作用而发生变化，导致曲折流变多。

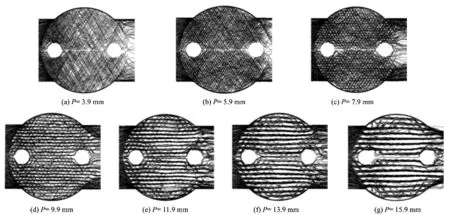
图6 壳程不同波纹节距流线图Figure 6 Flow diagram of shell side with different corrugated pitch

由图7可知，流体的速度沿中心线呈对称性分布。圆形板片角孔两侧速度较大，其余部分较小，且随节距的变大，角孔两侧的高速区域略有变大。这是由于角孔的阻挡使入口流体流向左右两侧，形成了小范围的流量聚集、扰流程度增大，使得流速增大；但随节距的变大，触点数目直线下降，扰流程度减小、流速减缓，使得流体的扩散速度变慢，导致了高速区的增大。此外，由于流态改变，角孔两侧的高速区也由顺着波纹纹路发展转为横向分布。深入观察可以发现，随节距增大，平均流速降低，触点后低速流动涡流区域逐渐扩大。这是由于流体随波纹节距的增大，曲折流幅度升高，漩涡变大，同时波纹陡度变缓，触点数降低，扰流变差，流速降低。

图7 壳程不同节距流速分布云图Figure 7 Cloud image of velocity distribution of different pitches on the shell side

2.2 不同波纹节距的湍动能

湍动能κ是表示流体湍流程度的参数，κ越大，湍流程度越剧烈。由图8可知，在同一雷诺数下，随波纹节距增大湍动能值逐渐减小，波纹节距为3.9 mm时湍动能最高。这是因为波纹节距的增大，导致波纹陡度下降、触点数目减少、扰动能力变差使得流速降低，造成湍动能减缓，这与前面流速分析一致。相同的波纹节距，湍动能随着雷诺数的增大而增大，但增幅逐渐减小。当波纹节距为3.9 mm时，随着雷诺数的增大，湍动能从0.018 6 m2/s2增大到0.155 5 m2/s2，增大了0.136 9 m2/s2；当波纹节距为15.9 mm时，湍动能从0.009 876 987 m2/s2增加到0.074 776 987 m2/s2，增大了0.064 9 m2/s2。波纹节距为3.9 mm时湍动能的增大值是波纹节距为15.9 mm时的2.1倍多。当雷诺数为8 705时，湍动能从0.155 498 360 m2/s2降低至0.074 776 987 m2/s2，减小了0.080 7 m2/s2；当雷诺数为2 374时，湍动能从0.018 6 m2/s2降到0.009 9 m2/s2，减小了0.008 7 m2/s2。雷诺数8 705时湍动能的减小值是雷诺数2 374时的9.3倍。由此可知：当波纹节距相同时，湍动能随雷诺数的增大而增大，且增值随节距变大而减小；降低雷诺数或者减小节距可以对流体扰动起到强化作用，提高流体的湍流强度。

图8 不同波纹节距的湍动能Figure 8 Turbulent kinetic energy of different corrugated pitch

2.3 不同波纹节距的阻力性能

对板壳式换热器的阻力性能分析，研究者通常采用压降来衡量阻力损失，为探明波纹节距对阻力性能的影响，课题组对压降的变化进行了研究，研究结果如图9所示。压降Δp表达式为

式中：Δp为压降，Pa；de为当量直径，mm；L为流道长度，m；f为摩擦因数；ρ为流体密度，kg/m3；v为流体流速，m/s。

由图9可知，在同一雷诺数下，随节距的增大，压降逐渐减小，这是因为随着节距的增大，触点数目下降，流体阻力性能减小使得压降减小；随雷诺数的增大，压降也增大。当雷诺数为2 374时，波纹节距从3.9 mm增大到15.9 mm，压降从21 136.34 Pa降低到5 298.49 Pa，压降降低了15 837.85 Pa；而当雷诺数为8 705时，压降从229 754.81 Pa降低到62 874.79 Pa ，压降降低了166 880.02 Pa。即雷诺数为8 705时压降的下降值是雷诺数为2 374时的10.54倍。从图中可知波纹节距为15.9 mm时压降较小，阻力性能较好。由此得出降低雷诺数或增大节距可以减小压降，对板壳式换热器的阻力性能有积极影响。

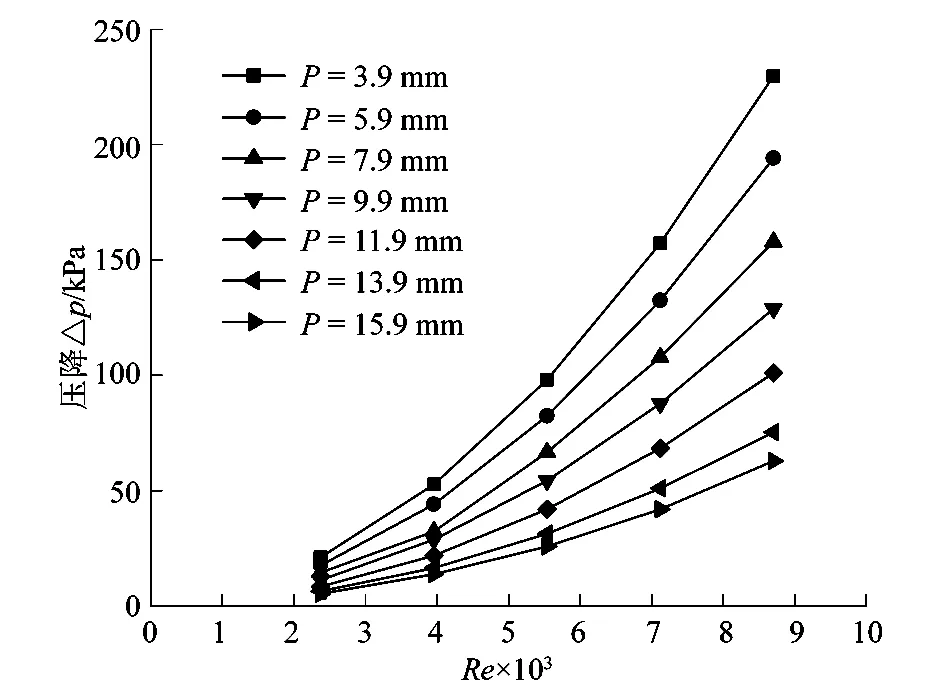
图9 不同波纹节距的压降Figure 9 Pressure drop at different corrugated pitch

3 结语

课题组通过改变波纹节距，模拟分析了板壳式换热器壳侧流体湍动能和压降的变化规律，得到了以下结论：随着波纹节距的增大，流体流线逐渐由十字交叉流转为曲折流，湍动能逐渐减小，并且在不同波纹节距时，随雷诺数的增大，湍动能逐渐增大，流动性能更优；随着波纹节距的增大，压降逐渐减小，并且在同一波纹节距下，随雷诺数的增大，压降逐渐增大，阻力性能更优；减小节距可以得到较好的流动性能，增大节距可以得到较好的阻力性能。

波纹节距、波纹高度和波纹角度是板壳式换热器重要的设计参数，研究者可进一步研究波纹高度和波纹角度对板壳式换热器流动性能和阻力性能的影响，及3者对板壳式换热器性能的综合影响，得出最佳设计参数。